El algoritmo de ordenamiento ideal

• Estable: No intercambia el orden de elementos con el mismo valor.
• No tiene overhead.
• En el peor de los casos tiene O(n log n) comparaciones.
• En el peor de los casos tiene O(n) intercambios.
• Flexible: La complejidad temporal tiende a O(n) cuando los datos están semi-ordenados o cuando hay pocas llaves únicas.

Ordenamiento por inserción

• Definición: Es una manera natural de ordenar datos. De la lista de n datos, se toma el elemento k y se compara con los k-1 anteriores para encontrar su posición.
• Complejidad espacial adicional: O(1)
• Complejidad temporal
  • Mejor de los casos: O(n)
  • Caso promedio: O(n^2)
  • Peor de los casos: O(n^2)
• Intercambios: O(n^2)

template<typename T_>
void insertionSort(T_ arr[], int length)
{
    for(int i = 1; i < length; i++)
    {
        // Invariante: a[1..i] está ordenado
        for(int j = i; j > 0 && arr[j] < arr[j - 1]; j--) 
        {
            T_ temp = arr[j];
            arr[j] = arr[j-1];
            arr[j-1] = temp;
        }
    }
}

Ejemplo

Ventajas

• Simple de implementar.
• Eficiente para conjuntos de datos reducidos o cuando los datos están semi-ordenados.
• El más efectivo que otros algoritmos de O(n^2).
• Estable.
• Requiere poco overhead.

Desventajas

• Complejidad temporal O(n^2) en promedio y en el peor de los casos.

Ordenamiento por selección

• Definición: En cada iteración se toma el menor de los números y se coloca en la posición k de la lista, donde k es el número de iteración.
• Complejidad espacial adicional: O(1)
• Complejidad temporal
  • Mejor de los casos: O(n^2)
  • Caso promedio: O(n^2)
  • Peor de los casos: O(n^2)
• Intercambios: O(n)

template<typename T_>
void selectionSort(T_ arr[], int length)
{
    for(int i = 0; i < length; i++)
    {
        int k = i;
        for(int j = i; j < length; j++)
        {
            if(arr[j] < arr[k])
            {
                // k es el índice
                // del elemento más pequeño
                // de arr[i...n]
                k = j;
            }
        }
        T_ temp = arr[i];
        arr[i] = arr[k];
        arr[k] = temp;
    }
}

Ventajas

• Simple de implementar.
• Reduce el número de comparaciones.

Desventajas

• No es estable.
• Complejidad temporal O(n^2) para todos los casos.

Ordenamiento Shell

• Definición: Ordena pares de elementos separados entre sí por una distancia considerable reduciendo con esto el espacio entre los elementos a comparar.
• Complejidad espacial adicional: O(1)
• Complejidad temporal
  • Mejor de los casos: O(n log^2 n)
  • Caso promedio: Siguiente diapositiva
  • Peor de los casos: O(n^2)

Secuencia de espacios

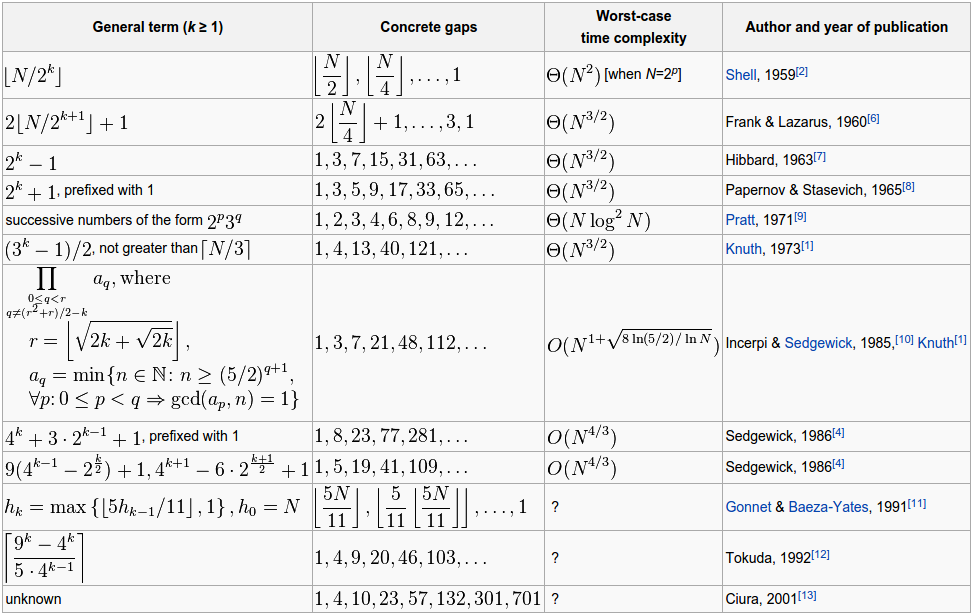
#include <QVector>

template<typename T_>
void shellSort(T_ arr[], int length)
{
    int gap = 1;
    QVector<int> gaps;
    while(gap < length)
    {
        gaps.append(gap);
        gap = gap * 3 + 1;
    }
    while(gaps.size() > 0)
    {
        int curGap = gaps.at(gaps.size() - 1);
        gaps.pop_back();
        // Invariante: a[0...curGap-1] ya están ordenados
        for(int i = curGap; i < length; ++i)
        {
            T_ temp = arr[i];
            int j;
            // Ordenamiento por inserción
            for(j = i - curGap; j >= 0 && arr[j] > temp; j -= curGap)
            {
                arr[j + curGap] = arr[j];
            }
            arr[j + curGap] = temp;
        }
    }
}

Ventajas

• La complejidad temporal depende de la secuencia de incremento utilizada.
• Requiere poco overhead.
• Implementación relativamente fácil.
• Complejidad temporal sub-cuadrática.

Desventajas

• Es un problema abierto, su mejor rendimiento en términos de complejidad temporal no ha sido encontrada.
• Su rendimiento no es siginificativamente mayor a otros algoritmos de ordenamiento.

Ordenamiento por mezcla

(Mergesort)

• Definición: Es un algoritmo de divide y vencerás. Divide la lista desordenada en subconjuntos, hasta llegar a subconjuntos de un elemento, comienza a ordenar los subconjuntos mientras los va mezclando, la última lista mezclada es la lista ordenada.
• Complejidad espacial adicional: O(n)
• Complejidad temporal
  • Mejor de los casos: O(n log n)
  • Caso promedio: O(n log n)
  • Peor de los casos: O(n log n)

template<typename T_>
void mergeSort(T_ arr[], int low, int high)
{
    if(low < high)
    {
        int mid = (low + high)/2;
        // Ordenar recursivamente 
        // las mitades del arreglo
        mergeSort(arr, low, mid);
        mergeSort(arr, mid + 1, high);
        // Mezclar las mitades del 
        // arreglo ordenadas
        merge(arr, low, mid, high);
    }
}

template<typename S_>
void merge(S_ arr[], int low, int mid, int high)
{
    S_ *b = new int[high - low + 1];
    int h = low;
    int i = 0;
    int j = mid +1;
    // Mezcla las dos mitades ordenadas en interaciones anteriores
    while(h <= mid && j <= high)
    {
        if(arr[h] <= arr[j])
        {
            b[i] = arr[h];
            ++h;
        }
        else
        {
            b[i] = arr[j];
            ++j;
        }
        ++i;
    }
    // Completa el arreglo con los valores restantes
    if(h > mid)
    {
        for(int k = j; k <= high; ++k)
        {
            b[i] = arr[k];
            ++i;
        }
    }
    else
    {
        for(int k = h; k <= mid; ++k)
        {
            b[i] = arr[k];
            ++i;
        }
    }
    // Mover la parte ordenada al arreglo original
    memcpy(arr + low, b, (high - low + 1) * sizeof(S_));
    delete[] b;
}

Ejemplo

Ventajas

• Simple de implementar.
• Estable (el único del tipo O(n log n)).
• Mejor rendimiento ordenando listas enlazadas (complejidad espacial adicional      O(log n)).

Desventajas

• Tiene overhead de O(n).
• No es flexible.

Ordenamiento por montículos

(Heapsort)

• Definición:  Se puede considerar como una versión mejorada de ordenamiento por selección. La diferencia radica en utilizar un montículo (heap) en lugar de una búsqueda lineal para encontrar el mínimo.
• Complejidad espacial adicional: O(1)
• Complejidad temporal:
  • Mejor de los casos: O(n log n)
  • Caso promedio: O(n log n)
  • Peor de los casos: O(n log n)

Concepto de montículo

La raíz está en 0. Por cada índice i, se cumple:

• Sus hijos están en los índices 2i+1 y 2i+2.
• Su padre está en floor((i-1)/2). (La raíz no tiene padre)

template<typename V_>
void siftDown(V_ arr[], int start, int end)
{
    int root = start;

    while(root * 2 + 1 <= end)
    {
        int child = root * 2 +1;
        int swap = root;

        if(arr[swap] < arr[child])
        {
            swap = child;
        }
        if(child + 1 <= end && arr[swap] < arr[child + 1])
        {
            swap = child + 1;
        }
        // Si la raíz es el elemento mayor de ese montículo,
        // quiere decir que el montículo está ordenado.
        if(swap == root)
        {
            return;
        }
        else
        {
            V_ temp = arr[swap];
            arr[swap] = arr[root];
            arr[root] = temp;
            root = swap;
        }
    }
}

template<typename S_>
void heapify(S_ arr[], int length)
{
    // Se obtiene el índice del padre del último nodo
    int start = floor((length - 2)/2);

    while(start >= 0)
    {
        // Ordenar el montículo cuya raíz es start
        siftDown(arr, start, length - 1);
        start -= 1; // Ir a un nodo superior.
    }
}

template<typename T_>
void heapSort(T_ arr[], int length)
{
    // Poner el elemento mayor del arreglo
    // como raíz del montículo
    heapify(arr, length);

    int end = length - 1;
    // Invariante: arr[0...end] es un montículo
    // y todo elemento después de end es mayor.
    // Por lo que arr[end...length - 1] está ordenado
    while(end > 0)
    {
        // arr[0] es el elemento más grande del arreglo
        // se moverá al frente de la parte ordenada del
        // arreglo.
        T_ temp = arr[0];
        arr[0] = arr[end];
        arr[end] = temp;

        end -= 1;

        // El intercambio arruinó el montículo,
        // por lo que hay que volver a ordenar.
        siftDown(arr, 0, end);
    }
}

Ejemplo

Ventajas

• Sencillo de implementar.
• Tiene overhead constante.
• Complejidad temporal es O(n log n).

Desventajas

• No es estable.
• No es flexible.

Ordenamiento rápido

(Quicksort)

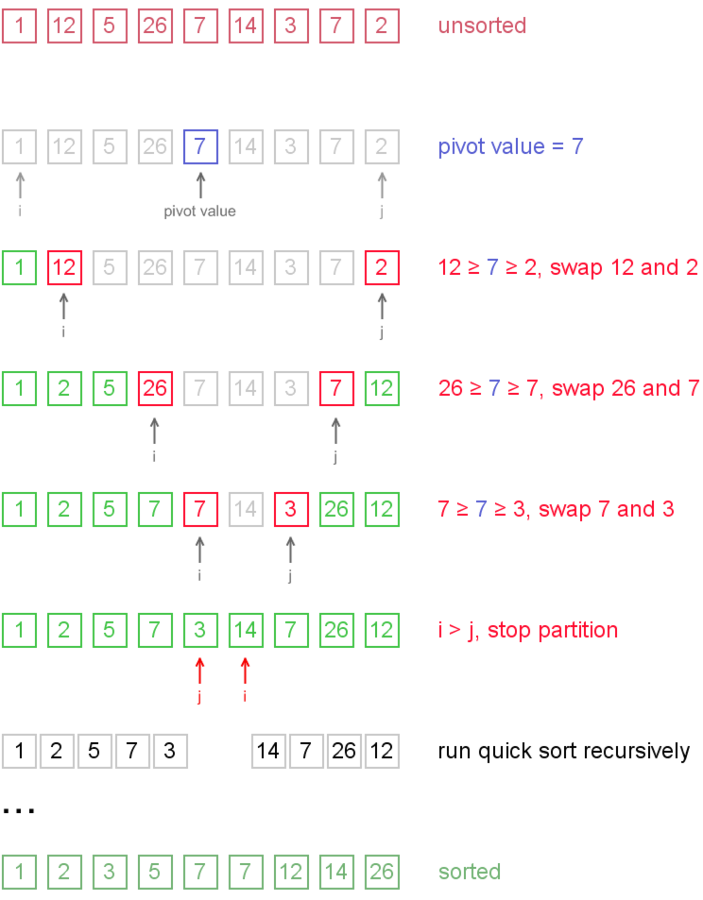
• Definición:  Es un algoritmo de divide y vencerás. Divide la lista desordenada en dos subconjuntos que se ordenan recursivamente en base a un pivote.
• Complejidad espacial adicional: O(n) o O(log n)
• Complejidad temporal:
  • Mejor de los casos: O(n log n)
  • Caso promedio: O(n log n)
  • Peor de los casos: O(n log n) amortizado

template<typename T_>
void quickSort(T_ arr[], int left, int right)
{
      int i = left;
      int j = right;
      T_ pivot = arr[(left + right) / 2];

      // Partición
      while (i <= j) {
          while (arr[i] < pivot)
          {
              ++i;
          }
          while (arr[j] > pivot)
          {
              --j;
          }
          if (i <= j)
          {
              T_ tmp = arr[i];
              arr[i] = arr[j];
              arr[j] = tmp;
              ++i;
              --j;
          }
      };

      // Recursión
      if (left < j)
      {
          quickSort(arr, left, j);
      }
      if (i < right)
      {
          quickSort(arr, i, right);
      }
}

Ventajas

• Poco overhead.

Desventajas

• No es estable.
• No es flexible.
• O(n^2) cuando hay pocas llaves únicas.
• Existe una mejor versión.

Ordenamiento rápido mejorado

(Quicksort 3-way partition)

• Definición:  Es un algoritmo de divide y vencerás. Divide la lista desordenada en tres subconjuntos que se ordenan recursivamente en base a un pivote.
• Complejidad espacial adicional: O(log n)
• Complejidad temporal:
  • Mejor de los casos: O(n log n)
  • Caso promedio: O(n log n)
  • Peor de los casos: O(n log n) amortizado

# choose pivot
swap a[n,rand(1,n)]

# 3-way partition
i = 1, k = 1, p = n
while i < p,
  if a[i] < a[n], swap a[i++,k++]
  else if a[i] == a[n], swap a[i,--p]
  else i++
end
→ invariant: a[p..n] all equal
→ invariant: a[1..k-1] < a[p..n] < a[k..p-1]

# move pivots to center
m = min(p-k,n-p+1)
swap a[k..k+m-1,n-m+1..n]

# recursive sorts
sort a[1..k-1]
sort a[n-p+k+1,n]

Ventajas

• Poco overhead.
• Es flexible.

Desventajas

• No es estable.