图 & 拓扑排序



图
- 定义
- 图与树非常相似
- 有向图 v.s. 无向图
- 面试问题
- 深度优先搜索, 广度优先搜索
- DAG (有向无环图)
- 拓扑排序



图的表示
- 图的节点
- 邻接矩阵
- |V| 个顶点, |V| * |V|的0和1的矩阵来表示图的邻接矩阵
- 邻接表
- |V| 个顶点, 每个顶点对应一个数组列表,其中包含相邻的顶点
- 对于无向图,邻接表需要使用2 * |E|的空间,对于有向图,邻接表需要使用|E|的空间
GraphNode {
int val;
List<GraphNode> neighbors;
}



图的表示
- 邻接矩阵
- 邻接表



1 0 0 0 0
0 1 0 1 1
0 0 1 0 0
0 1 0 1 0
0 1 0 0 1
1 0 0 1 0
0 1 0 1 0
1 0 1 0 1
0 1 0 1 0
0 1 0 0 1
1 2,3
2 1,5
3 1
4 5
5 2,4
1 3,5
2 1,5
3 1
4 5
5 1,3,4
拓扑排序
拓扑排序(有时缩写为 toposort)是指对一个有向图的顶点进行线性排序,使得对于每一条有向边(u,v),顶点 u 在排序结果中都出现在顶点 v 的前面。
- 维护一个 0 入度顶点集合
- 不断选择 0 入度顶点,移除其出边,将其加入集合中
- 如果所有顶点都被合并到 0 入度顶点集合中,那么拓扑排序结果被找到



课程表
你需要完成一共n门课程,它们的标号为0到n-1。
有些课程有先修课程,例如要先学习课程1才能学习课程0,这被表示为一个有序对:[0,1]。
给定课程总数以及一些先修课程的关系对,你能否完成所有课程?
示例:
[1, 0], possible; [[1,0], [0,1]], impossible.



课程表
在现实生活中我们该如何解决它?
- 首先画一张有先决条件顺序的有向图。
- 选择一个没有先决条件的课程,删除与它相关的所有先决条件关系。
- 重复上述操作,直到所有课程都被安排或没有0先决条件的课程存在为止。
- 如果还有未被选择的课程,则这些课程无法被安排。



课程表
public boolean canFinish(int numCourses, int[][] prerequisites) {
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
for (int i = 0; i < numCourses; i++) {
graph.add(new ArrayList<Integer>());
}
int[] preNum = new int[numCourses];
for (int i = 0; i < prerequisites.length; i++) {
graph.get(prerequisites[i][1]).add(prerequisites[i][0]);
preNum[prerequisites[i][0]]++;
}
for (int i = 0; i < numCourses; i++) {
boolean availableCourse = false;
for (int j = 0; j < numCourses; j++) {
if (preNum[j] == 0) {
for (int k : graph.get(j)) {
preNum[k]--;
}
availableCourse = true;
preNum[j] = -1; //this class won't be taken again
break;
}
}
if (!availableCourse) {
return false;
}
}
return true;
}


外星人字典
有一种新的外星语言使用拉丁字母表,但字母之间的顺序对你来说是未知的。你收到了一个字典中单词的列表,这些单词按照这种新语言的词典顺序进行了排序。请推导出这种语言中字母的顺序。
例如,
给定以下字典中的单词:
[ "wrt", "wrf", "er", "ett", "rftt"]
正确的字母顺序是: "wertf"。



外星人字典
我们需要做什么?
使用单词获取两个字母之间的优先级关系
使用拓扑排序获取这些字母的顺序信息
注意:
你可以假设所有字母都是小写字母。
如果顺序无效,则返回一个空字符串。
可能存在多个有效的字母顺序,任何一个都可以返回。



外星人字典
public String alienOrder(String[] words) {
Map<Character, Set<Character>> hm = new HashMap<>();
Set<Character> set = new HashSet<>();
Queue<Character> queue = new LinkedList<>();
StringBuilder result = new StringBuilder();
for (String word: words) {
char[] wordArray = word.toCharArray();
for (char c: wordArray) {
set.add(c);
}
}
for (Character c: set) {
hm.put(c, new HashSet<Character>());
}
for (int i = 0; i < words.length-1; i ++) {
int minLen = Math.min(words[i].length(), words[i+1].length());
int j = 0;
for(j = 0; j < minLen; j ++) {
if (words[i].charAt(j) != words[i+1].charAt(j)) {
hm.get(words[i+1].charAt(j)).add(words[i].charAt(j));
break;
}
}
//all same chars, shorter words go first
if (j == minLen && words[i].length() > words[i+1].length()) return "";
}



外星人字典
for(Map.Entry<Character, Set<Character>> entry: hm.entrySet()) {
if (entry.getValue().isEmpty()) {
queue.add(entry.getKey());
result.append(entry.getKey());
}
}
while(!queue.isEmpty()) {
Character c = queue.poll();
for(Map.Entry<Character, Set<Character>> entry: hm.entrySet()) {
if (entry.getValue().contains(c)) {
entry.getValue().remove(c);
if (entry.getValue().isEmpty()) {
queue.add(entry.getKey());
result.append(entry.getKey());
}
}
}
}
String finalResult = result.toString();
if (finalResult.length() == set.size()) {
return finalResult;
} else {
return "";
}
}


克隆无向图
克隆一个无向图。图中的每个节点都包含一个标签和它的邻居列表。
class UndirectedGraphNode {
int label;
List<UndirectedGraphNode> neighbors;
UndirectedGraphNode(int x) { label = x; neighbors = new ArrayList<UndirectedGraphNode>(); }
};



克隆无向图
使用BFS / DFS遍历所有节点
使用哈希映射来记住哪些节点已经访问过
对每个节点及其邻居进行克隆



A B
C D
A' B'
C' D'
D''
克隆无向图
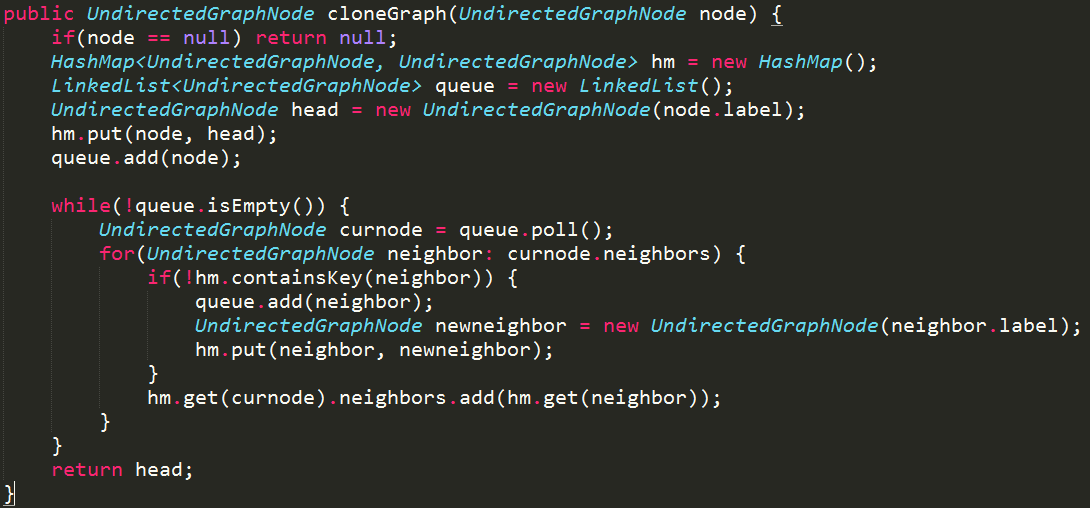



重构行程
给定一个航班机票列表,其中tickets[i]=[fromi, toi]表示一张航班的出发机场和到达机场。请重新构建这些机票的行程,并以顺序返回。
所有机票都属于一个人,他从“JFK”出发,因此行程必须以“JFK”开始。如果存在多个有效行程,则应返回读作单个字符串时字典序最小的行程。



重构行程



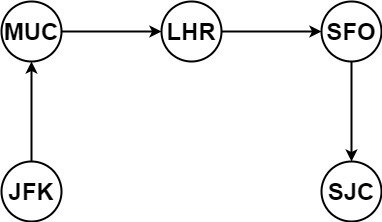

Input: tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]]
Output: ["JFK","MUC","LHR","SFO","SJC"]
Input: tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Output: ["JFK","ATL","JFK","SFO","ATL","SFO"]
Explanation: Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"] but it is larger in lexical order.
重构行程
所有边都已给定。我们如何知道应该走哪条路?
使用深度优先搜索(DFS)-> 迭代所有可能的路径并尝试找到所有路径
并使用某种方法来比较结果以获得最佳结果
我们应该如何存储数据-> 使用邻接表



重构行程



List<String> finalResult = new ArrayList<>();
public List<String> findItinerary(List<List<String>> tickets) {
Map<String, List<String>> graph = new HashMap<>();
for (int i = 0; i < tickets.size(); i ++) {
String start = tickets.get(i).get(0);
String end = tickets.get(i).get(1);
if (!graph.containsKey(start)) {
graph.put(start, new ArrayList<>());
}
graph.get(start).add(end);
}
for (Map.Entry<String, List<String>> entry: graph.entrySet()) {
Collections.sort(entry.getValue());
}
for (String start: graph.keySet()) {
if (start.equals("JFK")) {
List<String> result = new ArrayList<>();
result.add(start);
dfs(graph, start, result, 0, tickets.size());
}
}
return finalResult;
}剪枝



boolean dfs(Map<String, List<String>> graph, String start, List<String> result, int count, int total) {
if (count == total) {
if (finalResult.size() == 0 || compare(result, finalResult)) {
finalResult = new ArrayList<>(result);
}
return true;
}
if (!graph.containsKey(start) || graph.get(start).size() == 0) {
return false;
}
if (finalResult.size() > 0 && !compare(result, finalResult)) {
return false;
}
List<String> routes = graph.get(start);
boolean hasResult = false;
for (int i = 0; i < routes.size(); i ++) {
String cur = routes.get(i);
routes.remove(i);
result.add(cur);
hasResult = hasResult || dfs(graph, cur, result, count + 1, total);
result.remove(result.size() - 1);
routes.add(i, cur);
}
return hasResult;
}
boolean compare(List<String> result, List<String> finalResult) {
for (int i = 0; i < result.size(); i ++) {
int val = result.get(i).compareTo(finalResult.get(i));
if (val > 0) {
return false;
} else if (val < 0) {
return true;
}
}
return true;
}剪枝
最小高度树
对于具有树特征的无向图,我们可以选择任何节点作为根。结果图形将是一棵有根树。在所有可能的有根树中,那些高度最小的被称为最小高度树(MHT)。给定这样的图,编写一个函数来查找所有MHT并返回它们的根标签列表。
示例
给定 n = 4, edges = [[1, 0], [1, 2], [1, 3]], 返回 [1].
给定 n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]], 返回 [3, 4]
0
|
1
/ \
2 3
0 1 2
\ | /
3
|
4
|
5



最小高度树
-
计算每个节点的树高度
- O(|V| * |V|) -> 不够高效



最小高度树
一棵树最多可以拥有多少个最小高度树?
0
|
1
/ \
2 3
0
|
1
0 | 1 | 2
最多 2!



最小高度树
一棵树最多可以拥有多少个最小高度树?
我们可以使用反证法证明
如果有超过2个节点是根节点
我们只需要选择其中的3个节点。那么这三个节点一定会形成一个环,这与树的定义相矛盾



最小高度树
一棵树最多可以拥有多少个最小高度树?
我们可以使用反证法证明
m
h-m-n
h-m-n
n



h-m-n
最小高度树
- 移除所有的叶子节点
- 更新图形
- 重复上述过程,直到最多只剩下两个叶子节点



height = K
height = K
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
if (n < 1) return new ArrayList<>();;
ArrayList<HashSet<Integer>> graph = new ArrayList<>(n);
for (int i = 0; i < n; i++) {
graph.add(new HashSet<>());
}
for (int i = 0; i < edges.length; i++) {
graph.get(edges[i][0]).add(edges[i][1]);
graph.get(edges[i][1]).add(edges[i][0]);
}
Queue<Integer> leaves = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (graph.get(i).size() <= 1) {
leaves.add(i);
}
}
while (n > 2) {
n -= leaves.size();
Queue<Integer> newLeaves = new LinkedList<>();
while (!leaves.isEmpty()) {
Integer leaf = leaves.poll();
Integer neighbor = graph.get(leaf).iterator().next();
graph.get(neighbor).remove(leaf);
if (graph.get(neighbor).size() == 1) {
newLeaves.add(neighbor);
}
}
leaves = newLeaves;
}
return new ArrayList<>(leaves);
}


作业



【直通硅谷】10 图 & 拓扑排序
By ZhiTongGuiGu
【直通硅谷】10 图 & 拓扑排序
- 174



