Tree

Definition

A tree is a (possibly non-linear) data structure made up of nodes or vertices and edges without having any cycle.

Tree

Tree is one of the most important data structure in algorithms

Like our current File System

Tree has many different types

Tree

B Tree

Trie Tree

Binary Tree

BST

RB Tree

AVL

Terminology

Node
- Root
- Leaf
- Parent
- Child
- Siblings
- Ancestor
- Descendant
Edge
Height
Depth
Level
Path

Binary Tree

It is actually different from tree
It has right sub-tree and left sub-tree
Each node can have at most two children

Complete Binary Tree

Very useful in algorithm problems
Always assuming as a tree's property to compute the time complexity

Properties of Binary Tree

at Level i, at most 2^i nodes
a tree with height k, at most 2^k-1 nodes
a complete binary tree with n nodes, the height will be
If we number the node from root and base on the level, for a complete binary tree, we will have:
- for node number k, the left child is 2k+1
- for node number k, the right child is 2k+2
How to store a Binary Tree?

\left \lceil log_2(n+1) \right \rceil

Basic Data Structure of a Binary Tree

class Node:
    def __init__(self, data=None):
        self.data = data
        self.left = None
        self.right = None


class BinaryTree:
    def __init__(self, root_data):
        self.root = Node(root_data)

Traversal of a Binary Tree

PreOrder: Parent, left child, right child
InOrder: left child, Parent, right child
PostOrder: left child, right child, Parent

Traversal of a Binary Tree

PreOrder: A B D E H I C F G J

InOrder: D B H E I A F C G J

PostOrder: D H I E B F J G C A

Traversal of a Binary Tree

We need to use recursion to traverse a tree

def preorder(root):
    if root is not None:
        # Visit the node by printing the node data
        print(root.data, end=" ")
        preorder(root.left)
        preorder(root.right)

Traversal of a Binary Tree

def inorder(root):
    if root is not None:
        inorder(root.left)
        print(root.data, end=" ")
        inorder(root.right)

def postorder(root):
    if root is not None:
        postorder(root.left)
        postorder(root.right)
        print(root.data, end=" ")

Traversal of a Binary Tree

Can we use Stack to traverse the tree without recursion?

Traversal of a Binary Tree

Pre-order traversal: use a stack to simulate recursion, and print the node when it is first encountered.

Traversal of a Binary Tree

    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        
        stack, res = [], []
        
        while stack or root:
            while root:
                stack.append(root)  # first time 
                res.append(root.val)
                root = root.left
            
            if stack:
                top = stack.pop()
                if top.right:
                    root = top.right
        return res

/ \

2 3

/ \

4 5

Traversal of a Binary Tree

InOrder: What we should do?

InOrder: We push the node, go to left

If there is no left, we pop, print and push the right

Traversal of a Binary Tree

  def inorderTraversal(self, root: TreeNode) -> List[int]:
        stack = []
        res = []
        while root or stack:
            while root:
                stack.append(root)
                root = root.left
            if stack:
                root = stack.pop()
                res.append(root.val)
                root = root.right
        return res

Traversal of a Binary Tree

PostOrder: The most difficult one

PostOrder: go to left, when there is no left, visit it. Then for the top of the stack, do we visit it now?

No. Because it is what InOrder does

We need to then go to the right until there is nowhere to go, we visit it and then pop

Traversal of a Binary Tree

PostOrder: The most difficult one

Can we do the PostOrder just using the current structure?

No. We do not know the status of the top element in the stack. Has the right child been traversed or not?

Traversal of a Binary Tree

We need an additional flag to store the status of the node

static class NodeWithFlag {
	Node node;
	boolean flag;
	public NodeWithFlag(Node n, boolean value) {
		node = n;
		flag = value;
	}
}

After we visit the right child, we update the flag;

Traversal of a Binary Tree

Another way is to use a HashSet to store which node has been visited

First visit :HashSet.contains() == false -> put into set

Second visit: HashSet.contains == true -> output value

Construct a Binary Tree

If we have a traversal result of a tree, can we construct the tree?

PreOrder: A B C D

Construct a Binary Tree

No matter if you give a PreOrder, InOrder or PostOrder, it can construct different trees

What if we give two traversals?

Construct a Binary Tree

PreOrder: A B C D

InOrder: B A D C

Construct a Binary Tree

PreOrder: A B C D

PostOrder: B D C A

Construct a Binary Tree

Conclusion: You need two traversals to construct a tree, and one of them must be a InOrder traversal

How to construct a tree with a PreOrder and an InOrder?

Construct a Binary Tree

PreOrder: A B D E H I C F G J

InOrder: D B H E I A F C G J

A is root so A is the first in PreOrder, InOrder can use A to seperate left sub-tree and right sub-tree

Then we can do recursion

 public TreeNode buildTree(int[] preorder, int[] inorder) {
        final int preStart = 0;
        final int preEnd = preorder.length - 1;
        final int inStart = 0;
        final int inEnd = inorder.length - 1;

        return constructTree(preorder, preStart, preEnd, inorder, inStart, inEnd);
    }

    private TreeNode constructTree(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd) {
        // Base case: if there are no elements to construct the tree
        if (preStart > preEnd || inStart > inEnd) {
            return null;
        }

        // The first element of preorder is the root of the current subtree
        final int rootValue = preorder[preStart];
        TreeNode root = new TreeNode(rootValue);

        // Find the position of the root in inorder to determine the boundaries of left and right subtrees
        int inorderRootIndex = 0;
        for (int i = inStart; i <= inEnd; i++) {
            if (inorder[i] == rootValue) {
                inorderRootIndex = i;
                break;
            }
        }

        // Number of nodes in the left subtree
        final int leftSubtreeSize = inorderRootIndex - inStart;

        // Recursively construct the left and right subtrees
        root.left = constructTree(preorder, preStart + 1, preStart + leftSubtreeSize, inorder, inStart, inorderRootIndex - 1);
        root.right = constructTree(preorder, preStart + leftSubtreeSize + 1, preEnd, inorder, inorderRootIndex + 1, inEnd);

        return root;
    }

PreOrder + InOrder

def buildTree(preorder, inorder):
    preStart = 0
    preEnd = len(preorder) - 1
    inStart = 0
    inEnd = len(inorder) - 1

    return construct(preorder, preStart, preEnd, inorder, inStart, inEnd)

def construct(preorder, preStart, preEnd, inorder, inStart, inEnd):
    if preStart > preEnd or inStart > inEnd:
        return None

    val = preorder[preStart]
    p = TreeNode(val)
    k = 0
    for i in range(inStart, inEnd + 1):
        if val == inorder[i]:
            k = i
            break

    p.left = construct(preorder, preStart + 1, preStart + (k - inStart), inorder, inStart, k - 1)
    p.right = construct(preorder, preStart + (k - inStart) + 1, preEnd, inorder, k + 1, inEnd)
    return p

Construct a Binary Tree

PostOrder: D H I E B F J G C A

InOrder: D B H E I A F C G J

It is similar as PreOrder + InOrder, the only difference is the root now is the last one in PostOrder

PostOrder + InOrder

public TreeNode buildTree(int[] inorder, int[] postorder) {
        int inStart = 0;
        int inEnd = inorder.length - 1;
	int postStart = 0;
        int postEnd = postorder.length - 1;
	return build(inorder, inStart, inEnd, postorder, postStart, postEnd);
}
public TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {
	if (inStart > inEnd || postStart > postEnd)
		return null;
 
	int rootValue = postorder[postEnd];
	TreeNode root = new TreeNode(rootValue);
 
	int k = 0;
	for (int i = inStart; i <=inEnd; i++) {
		if (inorder[i] == rootValue) {
			k = i;
			break;
		}
	}
 
	root.left = build(inorder, inStart, k - 1, postorder, postStart,
			postStart + k - (inStart + 1));
	root.right = build(inorder, k + 1, inEnd, postorder, postStart + k- inStart, postEnd - 1);
	return root;
}

PostOrder + InOrder

def buildTree(inorder, postorder):
    inStart = 0
    inEnd = len(inorder) - 1
    postStart = 0
    postEnd = len(postorder) - 1
    return build(inorder, inStart, inEnd, postorder, postStart, postEnd)

def build(inorder, inStart, inEnd, postorder, postStart, postEnd):
    if inStart > inEnd or postStart > postEnd:
        return None

    rootValue = postorder[postEnd]
    root = TreeNode(rootValue)

    k = 0
    for i in range(inStart, inEnd + 1):
        if inorder[i] == rootValue:
            k = i
            break

    root.left = build(inorder, inStart, k - 1, postorder, postStart, postStart + k - (inStart + 1))
    root.right = build(inorder, k + 1, inEnd, postorder, postStart + k - inStart, postEnd - 1)
    return root

Binary Search Tree

All the sub-tree are BST
All elements in left sub-tree is small than root
All elements in Right sub-tree is larger than root
If we do InOrder traversal, the result of BST is a sorted array

Binary Search Tree

Find
Add
Remove

Binary Search Tree

Find 24

30 > 24 -> go to left
18 < 24 -> go to right
find 24, return true

Find 42

30 < 42 -> go to right
34 < 42 -> go to right
40 < 42 -> go to right
47 > 42 -> go to left
nothing on left, return false

Binary Search Tree

def find(value, root):
    node = root
    while node is not None:
        if node.data > value:
            node = node.leftNode
        elif node.data < value:
            node = node.rightNode
        else:
            return True
    return False

Binary Search Tree

Add 42

First we need to make sure if there is 42 in the tree already
Find the place we put 42

Binary Search Tree

def add(value, root):
    if root is None:
        root = Node(value)
        return True
    
    node = root
    while node is not None:
        if node.data > value:
            if node.leftNode is not None:
                node = node.leftNode
            else:
                node.leftNode = Node(value)
                return True
        elif node.data < value:
            if node.rightNode is not None:
                node = node.rightNode
            else:
                node.rightNode = Node(value)
                return True
        else:
            return False
    return False

Binary Search Tree

What is the time complexity for finding and adding some element into the tree?

Binary Search Tree

Remove 27

First we need to make sure if there is 27 in the tree already
We need to remove 27

Remove 30

How do we remove something that is not a leaf?

Binary Search Tree

If Q is a leaf
If Q has one child
- if the child R is the right child
- if the child R is the left child
if Q has two children

Binary Search Tree

P<R<Q

P<Q<R

R<Q<P

Q<R<P

Just use R to replace Q

Binary Search Tree

if we remove Q, which is the best substitute?

Binary Search Tree

Consider the inOrder traversal, the one just before Q and the one just after Q are the best candidates, since if they replace Q, when we do the inOrder again, the output is still an sorted array, which means the tree is still a BST.

So where are these two nodes?

Binary Search Tree

So for the element before Q, it is the largest node in sub-tree R1

The element after Q, it is the smallest node in sub-tree R2

Does that node have child? Canwe remove them directly

Maybe, but at most one, so we go back to condition 2

def remove(value, root):
    if root is None:
        return False
    if root.data == value:
        root = removeNode(root)
        return True
    
    node = root
    while node is not None:
        if node.data > value:
            if node.leftNode is not None and node.leftNode.data != value:
                node = node.leftNode
            elif node.leftNode is None:
                return False
            else:
                node.leftNode = removeNode(node.leftNode)
                return True
        elif node.data < value:
            if node.rightNode is not None and node.rightNode.data != value:
                node = node.rightNode
            elif node.rightNode is None:
                return False
            else:
                node.rightNode = removeNode(node.rightNode)
                return True
        else:
            return False
    return False

Binary Search Tree(cont)

def removeNode(node):
    if node.leftNode == None and node.rightNode == None:
        return None
    elif node.leftNode == None:
        return node.rightNode
    elif node.rightNode == None:
        return node.leftNode
    else:
        node.data = findAndRemove(node)
        return node

def findAndRemove(node):
    result = 0
    if node.leftNode.rightNode == None:
        result = node.leftNode.data
        node.leftNode = node.leftNode.leftNode
        return result
    node = node.leftNode
    while node.rightNode.rightNode != None:
        node = node.rightNode
    result = node.rightNode.data
    node.rightNode = node.rightNode.leftNode
    return result

Binary Search Tree

We know the search time is highly related to the height of the tree

If we keep add and remove elements in the tree, the tree will become unbalanced

So we have Red-black tree and AVL tree, they could use rotation and reconstruct to make the tree balance.

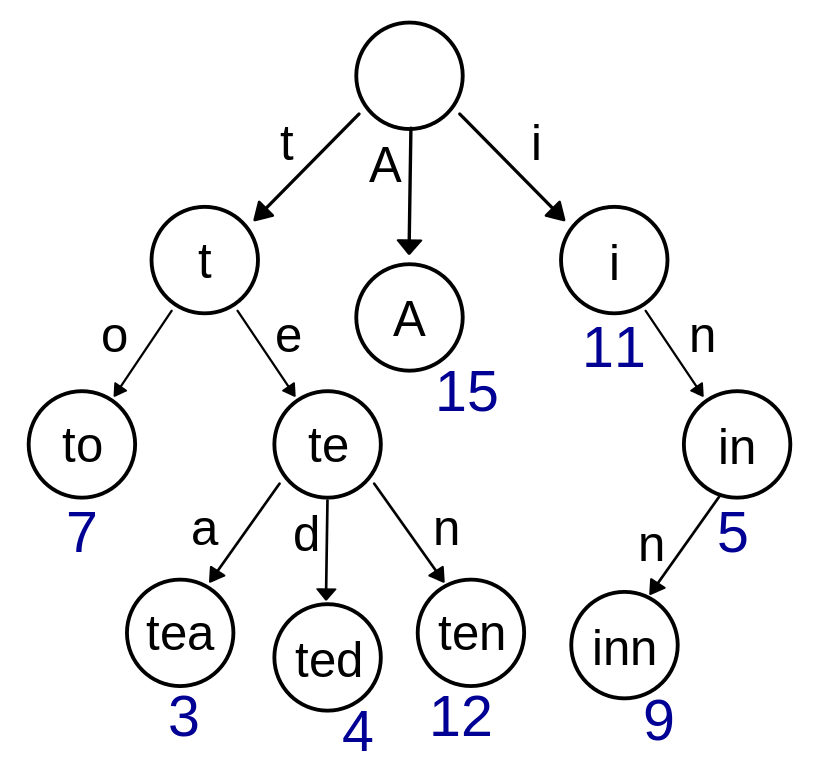
Trie Tree

In computer science, a trie, also called digital tree and sometimes radix tree or prefix tree (as they can be searched by prefixes), is an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings.

What Trie Tree Can Help?

It can store a dictionary in a good way without consuming much additional space
It can easily find common prefix for two strings (this is very useful in typeahead)
It can use easily find if a word is in the dictionary (maintain the order)

Complexity Analysis

In the insertion and finding notice that lowering a single level in the tree is done in constant time, and every time that the program lowers a single level in the tree, a single character is cut from the string.

we can conclude that every function lowers L levels on the tree and every time that the function lowers a level on the tree, it is done in constant time, then the insertion and finding of a word in a trie can be done in O(L) time.

The memory used in the tries depends on the methods to store the edges and how many words have prefixes in common.

Implement Trie (Prefix Tree)

Implement a trie with insert, search, and startsWith methods

We only use lowercase 'a' to 'z'

How many children does a node have?

Implement Trie (Prefix Tree)

class TrieNode:
    def __init__(self):
        self.isWord = False
        self.children = [None] * 26

Implement Trie (Prefix Tree)

class Trie:
    def __init__(self):
        self.root = TrieNode()

    def insert(self, word):
        if word is None or len(word) == 0:
            return
        pNode = self.root
        for i in range(len(word)):
            c = word[i]
            index = ord(c) - ord('a')
            if pNode.children[index] is None:
                newNode = TrieNode()
                pNode.children[index] = newNode
            pNode = pNode.children[index]
        pNode.isWord = True

Implement Trie (Prefix Tree)

def search(self, word):
    pNode = self.root
    if word is None or len(word) == 0:
        return True
    for i in range(len(word)):
        index = ord(word[i]) - ord('a')
        pNode = pNode.children[index]
        if pNode is None:
            return False
    return pNode.isWord

def startsWith(self, prefix):
    pNode = self.root
    if prefix is None or len(prefix) == 0:
        return True
    for i in range(len(prefix)):
        index = ord(prefix[i]) - ord('a')
        pNode = pNode.children[index]
        if pNode is None:
            return False
    return True

Design In-Memory File System

Design an in-memory file system to simulate the following functions:

ls: Given a path in string format. If it is a file path, return a list that only contains this file's name. If it is a directory path, return the list of file and directory names in this directory. Your output (file and directory names together) should in lexicographic order.

mkdir: Given a directory path that does not exist, you should make a new directory according to the path. If the middle directories in the path don't exist either, you should create them as well. This function has void return type.

addContentToFile: Given a file path and file content in string format. If the file doesn't exist, you need to create that file containing given content. If the file already exists, you need to append given content to original content. This function has void return type.

readContentFromFile: Given a file path, return its content in string format.

Design In-Memory File System

We mentioned File System is a tree.

And file system can have many children under each node. So using Trie tree is a good way to represent it.

class TrieNode:
    def __init__(self):
        self.isFile = False
        self.content = ""
        self.children = {}

Design In-Memory File System

class FileSystem:
    def __init__(self):
        self.root = TrieNode()

    def ls(self, path):
        results = []
        cur = self.root
        routes = path.split("/")
        for i in range(1, len(routes)):
            cur = cur.children.get(routes[i])
        if cur.isFile:
            results.append(routes[-1])
        else:
            results.extend(cur.children.keys())
            results.sort()
        return results

    def mkdir(self, path):
        self.get_current_node(path)

Design In-Memory File System

class FileSystem:
    def __init__(self):
        self.root = TrieNode()

    def addContentToFile(self, filePath, content):
        cur = self.get_current_node(filePath)
        cur.isFile = True
        if cur.content is None:
            cur.content = content
        else:
            cur.content += content

    def readContentFromFile(self, filePath):
        cur = self.get_current_node(filePath)
        return cur.content

    def get_current_node(self, path):
        cur = self.root
        routes = path.split("/")
        for i in range(1, len(routes)):
            if routes[i] not in cur.children:
                cur.children[routes[i]] = TrieNode()
            cur = cur.children[routes[i]]
        return cur

Word Search II

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

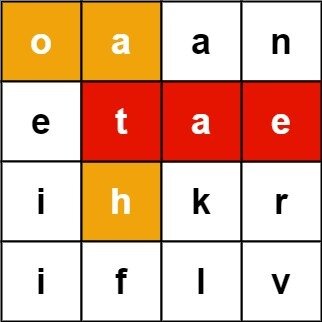
Example:
Input:
board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]]
words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Word Search II

class TrieNode:
    def __init__(self):
        self.children = [None] * 26
        self.isWord = False
        self.word = None

class Trie:
    def __init__(self):
        self.root = TrieNode()
    
    def insert(self, word):
        cur = self.root
        for char in word:
            c = ord(char) - ord('a')
            if not cur.children[c]:
                cur.children[c] = TrieNode()
            cur = cur.children[c]
        cur.isWord = True
        cur.word = word

Word Search II

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        trie = Trie()
        for word in words:
            trie.insert(word)
        
        m = len(board)
        n = len(board[0])
        visited = [[False for _ in range(n)] for _ in range(m)]
        results = set()
        
        def search(trienode, x, y):
            nonlocal m, n
            if trienode.isWord:
                results.add(trienode.word)
            visited[x][y] = True
            for dx, dy in [(1, 0), (0, 1), (-1, 0), (0, -1)]:
                nx, ny = x + dx, y + dy
                if 0 <= nx < m and 0 <= ny < n and not visited[nx][ny]:
                    c = ord(board[nx][ny]) - ord('a')
                    if trienode.children[c]:
                        search(trienode.children[c], nx, ny)
            visited[x][y] = False
        
        for i in range(m):
            for j in range(n):
                c = ord(board[i][j]) - ord('a')
                if trie.root.children[c]:
                    search(trie.root.children[c], i, j)
        
        return list(results)

Other Kinds of Tries

We used the tries to store words with lowercase letters, but the tries can be used to store many other things. We can use bits or bytes instead of lowercase letters and every data type can be stored in the tree, not only strings.

Tree

Definition

Tree

Tree

Terminology

Binary Tree

Complete Binary Tree

Properties of Binary Tree

Basic Data Structure of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Traversal of a Binary Tree

Construct a Binary Tree

Construct a Binary Tree

Construct a Binary Tree

Construct a Binary Tree

Construct a Binary Tree

Construct a Binary Tree

PreOrder + InOrder

Construct a Binary Tree

PostOrder + InOrder

PostOrder + InOrder

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree(cont)

Binary Search Tree

Binary Search Tree

Trie Tree

Trie Tree

Trie Tree

What Trie Tree Can Help?

Complexity Analysis

Implement Trie (Prefix Tree)

Implement Trie (Prefix Tree)

Implement Trie (Prefix Tree)

Implement Trie (Prefix Tree)

Design In-Memory File System

Design In-Memory File System

Design In-Memory File System

Design In-Memory File System

Word Search II

Word Search II

Word Search II

Other Kinds of Tries

Python [Jo] Tree 05

More from ZhiTongGuiGu