Recursion
What is recursion
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem (as opposed to iteration).
How to solve a problem
- Divide into small problems.
- Solve small problems.
- Use the result of small problems to solve the original problem.
- If the small problems are the same as original one, just scale is different. Then this is called recursion.
Recursion Properties
- Base case
- simple scenario that does not need recursion to produce an answer.
- Recursion
- a set of rules that reduce all other case toward the base case.
Code problem with recursion
- Base case
- recursion rules
-
Represent the problem with coding function.
-
Define the essential parameters
- Parameters that define the problem.
- Parameters that store the temporary result or state.
- Define the return value
-
Define the essential parameters
- Fibonacci Number
- Can be solved by DP, which is better
- Climbing Stairs
- Same as Fibonacci
- Merge Sort
- We will talk more about that in Sort
Classical Recursion Problem
Problem
sub-problem-1
base-problem
sub-problem-2
sub-problem-3
sub-sub-problem-2
sub-sub-sub-problem
sub-sub-problem-1
...
...
...
Problem
sub-problem-1
sub-sub-problem
sub-sub-sub-problem
base-problem
Problem
sub-problem-1
base-problem
sub-problem-2
sub-problem-3
sub-sub-problem-2
sub-sub-sub-problem
sub-sub-problem-1
...
...
...
Problem
sub-problem-1
sub-sub-problem
sub-sub-sub-problem
base-problem
Problem
sub-problem-1
base-problem
sub-problem-2
sub-problem-3
sub-sub-problem-2
sub-sub-sub-problem
sub-sub-problem-1
...
...
...
Problem
sub-problem-1
sub-sub-problem
sub-sub-sub-problem
base-problem
Problem
sub-problem-1
base-problem
sub-problem-2
sub-problem-3
sub-sub-problem-2
sub-sub-sub-problem
sub-sub-problem-1
...
...
...
Problem
sub-problem-1
sub-sub-problem
sub-sub-sub-problem
base-problem
Problem
sub-problem-1
base-problem
sub-problem-2
sub-problem-3
sub-sub-problem-2
sub-sub-sub-problem
sub-sub-problem-1
...
...
...
Problem
sub-problem-1
sub-sub-problem
sub-sub-sub-problem
base-problem
Problem
sub-problem-1
sub-sub-problem
sub-sub-sub-problem
base-problem
Problem
sub-problem-1
base-problem
sub-problem-2
sub-problem-3
sub-sub-problem-2
sub-sub-sub-problem
sub-sub-problem-1
...
...
...
Backtracking
Recursion with one sub problem
Recursion with 1 sub problem does not have to use recursion
We can think about using iteration instead
int Factorial(int n, int total) {
if(n == 1) return 1;
return n * Factorial(n-1, n * total);
}int Factorial(int n) {
int sum = 1;
for(int i = 1; i <= n; i ++) {
sum = sum * i;
}
return sum;
}def factorial(n):
if n == 1:
return total
return n * factorial(n-1)def factorial(n):
sum = 1
for i in range(1, n+1):
sum = sum * i
return sumGray Code
The gray code is a binary numeral system where two successive values differ in only one bit.
Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.
For example, given n = 2, return [0,1,3,2]
This is a typical problem with only one sub-problem
You need to find the pattern inside of it.
What is gray code: a form of binary that uses a different method of incrementing from one number to the next
Example: 000 001 011 010 110 111 101 100
0 1 3 2 6 7 5 4
Gray Code
The gray code is a binary numeral system where two successive values differ in only one bit.
Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.
For example, given n = 2, return [0,1,3,2]
n=2
0
1
3
2
n=3
0
1
3
2
6
7
5
4
Symmetric
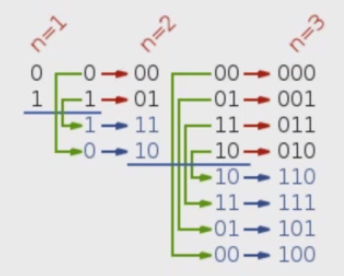
Gray Code
public List<Integer> grayCode(int n) {
List<Integer> result = new ArrayList<>();
helper(n, result);
return result;
}
public void helper(int n, List<Integer> result) {
if (n == 0) {
result.add(0);
return;
}
helper(n-1, result);
int size = result.size();
int k = 1 << (n - 1);
for (int i = size - 1; i >= 0; i --) {
result.add(result.get(i) + k);
}
return;
}The key is to find the relationship between each sub-problem
hold the result
Gray Code
The key is to find the relationship between each sub-problem
def gray_code(n):
result = []
helper(n, result)
return result
def helper(n, result):
if n == 0:
result.append(0)
return
helper(n-1, result)
size = len(result)
k = 1 << (n - 1)
for i in range(size - 1, -1, -1):
result.append(result[i] + k)
returnGray Code
def grayCode(self, n: int) -> List[int]:
if n == 0:
return [0]
res = self.grayCode(n - 1)
# add = 2 ** (n - 1) # this also works
add = 1 << (n - 1)
for i in range(len(res) - 1, -1, -1):
res.append(res[i] + add)
return resGray Code
public List<Integer> grayCode(int n) {
List<Integer> result = new ArrayList<>();
result.add(0);
for(int i = 0; i < n; i ++) {
int k = 1 << i;
int size = result.size();
for(int j = size - 1; j >= 0; j --) {
result.add(result.get(j) + k);
}
}
return result;
}We actually could get rid of the recursion code.
Should we use recursion or iteration?
Same as recursion, why?
Pow(x, n)
Implement pow(x, n), which calculates x raised to the power n (i.e., xn).
Input: x = 2.00000, n = 10
Output: 1024.00000
Input: x = 2.10000, n = 3
Output: 9.26100
Input: x = 2.00000, n = -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25
Pow(x, n)
def myPow(self, x: float, n: int) -> float:
if n == 0:
return 1
if n == 1:
return x
if n < 0:
return self.myPow(1 / x, -n)
if n % 2:
return self.myPow(x * x, n // 2) * x
else:
return self.myPow(x * x, n // 2) Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Example Input:
Start Point: (0, 0); Target Point (5, 5);
Maze: char[][] = {
{'.', 'X', '.', '.', '.', 'X'},
{'.', '.', '.', 'X', '.', 'X'},
{'X', 'X', '.', 'X', '.', '.'},
{'.', 'X', 'X', 'X', '.', 'X'},
{'.', '.', '.', '.', '.', 'X'},
{'.', '.', '.', '.', '.', '.'}
}
Example Output: True
Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Example Input:
Start Point: (0, 0); Target Point (5, 5);
Maze: char[][] = {
{'.', 'X', '.', '.', '.', 'X'},
{'.', '.', '.', 'X', '.', 'X'},
{'X', 'X', '.', 'X', '.', '.'},
{'.', 'X', 'X', 'X', '.', 'X'},
{'.', '.', '.', '.', '.', 'X'},
{'.', '.', '.', '.', '.', '.'}
}
Example Output: True
Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Consider what are valid subproblem?
What direction can it go?
- Out of Bound
- Wall
Maze
Given a maze and a start point and a target point, return whether the target can be reached.
- Out of Bound
- Wall
-
Visited
- (1, 2) -> (2, 2) -> (1, 2) -> (2, 2) -> ...
- Why we cannot go visited place?
Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Maze
Given a maze and a start point and a target point, return whether the target can be reached.
public static boolean solveMaze(char[][] maze,
int startX, int startY, int targetX, int targetY,
boolean[][] visited) {
if (startX < 0 || startX >= maze.length ||
startY < 0 || startY >= maze[0].length ||
maze[startX][startY] == 'X' || visited[startX][startY]) {
return false;
}
if (startX == targetX && startY == targetY) {
return true;
}
visited[startX][startY] = true;
if (solveMaze(maze, startX + 1, startY, targetX, targetY, visited) ||
solveMaze(maze, startX, startY + 1, targetX, targetY, visited) ||
solveMaze(maze, startX - 1, startY, targetX, targetY, visited) ||
solveMaze(maze, startX, startY - 1, targetX, targetY, visited)) {
return true;
}
return false;
}Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Does the base case order matter?
Maze
Given a maze and a start point and a target point, return whether the target can be reached.
def solve_maze(maze, startX, startY, targetX, targetY, visited):
if (startX < 0 or startX >= len(maze) or
startY < 0 or startY >= len(maze[0]) or
maze[startX][startY] == 'X' or visited[startX][startY]):
return False
if startX == targetX and startY == targetY:
return True
visited[startX][startY] = True
if (solve_maze(maze, startX + 1, startY, targetX, targetY, visited) or
solve_maze(maze, startX, startY + 1, targetX, targetY, visited) or
solve_maze(maze, startX - 1, startY, targetX, targetY, visited) or
solve_maze(maze, startX, startY - 1, targetX, targetY, visited)):
return True
return Falsepublic static boolean solveMaze(char[][] maze,
int startX, int startY, int targetX, int targetY) {
if (startX < 0 || startX >= maze.length ||
startY < 0 || startY >= maze[0].length ||
maze[startX][startY] == 'X') {
return false;
}
if (startX == targetX && startY == targetY) {
return true;
}
maze[startX][startY] = 'X';
if (solveMaze(maze, startX + 1, startY, targetX, targetY) ||
solveMaze(maze, startX, startY + 1, targetX, targetY) ||
solveMaze(maze, startX - 1, startY, targetX, targetY) ||
solveMaze(maze, startX, startY - 1, targetX, targetY)) {
return true;
}
return false;
}Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Optimization 1: reuse the maze to reduce the space complexity
Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Optimization 1: reuse the maze to reduce the space complexity
def solve_maze(maze, startX, startY, targetX, targetY):
if (startX < 0 or startX >= len(maze) or
startY < 0 or startY >= len(maze[0]) or
maze[startX][startY] == 'X'):
return False
if startX == targetX and startY == targetY:
return True
maze[startX][startY] = 'X'
if (solve_maze(maze, startX + 1, startY, targetX, targetY) or
solve_maze(maze, startX, startY + 1, targetX, targetY) or
solve_maze(maze, startX - 1, startY, targetX, targetY) or
solve_maze(maze, startX, startY - 1, targetX, targetY)):
return True
return Falsepublic static boolean solveMaze(char[][] maze,
int startX, int startY, int targetX, int targetY) {
if (startX < 0 || startX >= maze.length ||
startY < 0 || startY >= maze[0].length ||
maze[startX][startY] == 'X') {
return false;
}
if (startX == targetX && startY == targetY) {
return true;
}
maze[startX][startY] = 'X';
int[] dx = {1, 0, -1, 0};
int[] dy = {0, 1, 0, -1};
for (int i = 0; i < 4; i++) {
if (solveMaze(maze, startX + dx[i], startY + dy[i], targetX, targetY)) {
return true;
}
}
return false;
}Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Optimization 2: code style
Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Optimization 2: code style
def solve_maze(maze, startX, startY, targetX, targetY):
if (startX < 0 or startX >= len(maze) or
startY < 0 or startY >= len(maze[0]) or
maze[startX][startY] == 'X'):
return False
if startX == targetX and startY == targetY:
return True
maze[startX][startY] = 'X'
dx = [1, 0, -1, 0]
dy = [0, 1, 0, -1]
for i in range(4):
if solve_maze(maze, startX + dx[i], startY + dy[i], targetX, targetY):
return True
return Falsepublic static boolean solveMaze(char[][] maze,
int startX, int startY, int targetX, int targetY) {
if (startX == targetX && startY == targetY) {
return true;
}
maze[startX][startY] = 'X';
int[] dx = {1, 0, -1, 0};
int[] dy = {0, 1, 0, -1};
for (int i = 0; i < 4; i++) {
int newX = startX + dx[i], newY = startY + dy[i];
if (newX < 0 || newX >= maze.length || newY < 0 || newY >= maze.length ||
maze[newX][newY] == 'X') {
continue;
}
if (solveMaze(maze, newX, newY, targetX, targetY)) {
return true;
}
}
return false;
}Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Optimization 3: move the base case -> is it good?
Maze
Given a maze and a start point and a target point, return whether the target can be reached.
Optimization 3: move the base case -> is it good?
def solve_maze(maze, startX, startY, targetX, targetY):
if startX == targetX and startY == targetY:
return True
maze[startX][startY] = 'X'
dx = [1, 0, -1, 0]
dy = [0, 1, 0, -1]
for i in range(4):
newX, newY = startX + dx[i], startY + dy[i]
if (newX < 0 or newX >= len(maze) or
newY < 0 or newY >= len(maze[0]) or
maze[newX][newY] == 'X'):
continue
if solve_maze(maze, newX, newY, targetX, targetY):
return True
return Falsepublic static boolean solveMaze(char[][] maze,
int startX, int startY, int targetX, int targetY,
String path) {
if (startX < 0 || startX >= maze.length ||
startY < 0 || startY >= maze[0].length ||
maze[startX][startY] == 'X') {
return false;
}
if (startX == targetX && startY == targetY) {
System.out.println(path);
return true;
}
maze[startX][startY] = 'X';
int[] dx = {1, 0, -1, 0};
int[] dy = {0, 1, 0, -1};
char[] direction = {'D', 'R', 'U', 'L'};
for (int i = 0; i < 4; i++) {
String newPath = path + direction[i] + " ";
if (solveMaze(maze, startX+dx[i], startY+dy[i], targetX, targetY, newPath)) {
return true;
}
}
return false;
}Maze
Given a maze and a start point and a target point, print out the path to reach the target.
Maze
Given a maze and a start point and a target point, print out the path to reach the target.
def solve_maze(maze, startX, startY, targetX, targetY, path):
if (startX < 0 or startX >= len(maze) or
startY < 0 or startY >= len(maze[0]) or
maze[startX][startY] == 'X'):
return False
if startX == targetX and startY == targetY:
print(path)
return True
maze[startX][startY] = 'X'
dx = [1, 0, -1, 0]
dy = [0, 1, 0, -1]
direction = ['D', 'R', 'U', 'L']
for i in range(4):
newPath = path + direction[i] + " "
if solve_maze(maze, startX + dx[i], startY + dy[i], targetX, targetY, newPath):
return True
return Falsepublic static boolean solveMaze(char[][] maze,
int startX, int startY, int targetX, int targetY,
ArrayList<Character> path) {
if (startX < 0 || startX >= maze.length ||
startY < 0 || startY >= maze[0].length ||
maze[startX][startY] == 'X') {
return false;
}
if (startX == targetX && startY == targetY) {
return true;
}
maze[startX][startY] = 'X';
int[] dx = {1, 0, -1, 0};
int[] dy = {0, 1, 0, -1};
char[] direction = {'D', 'R', 'U', 'L'};
for (int i = 0; i < 4; i++) {
path.add(direction[i]);
if (solveMaze(maze, startX+dx[i], startY+dy[i], targetX, targetY, path)) {
return true;
}
path.remove(path.size()-1);
}
return false;
}Maze
Given a maze and a start point and a target point, return the path to reach the target.
Maze
Given a maze and a start point and a target point, return the path to reach the target.
def solve_maze(maze, startX, startY, targetX, targetY, path):
if (startX < 0 or startX >= len(maze) or
startY < 0 or startY >= len(maze[0]) or
maze[startX][startY] == 'X'):
return False
if startX == targetX and startY == targetY:
return True
maze[startX][startY] = 'X'
dx = [1, 0, -1, 0]
dy = [0, 1, 0, -1]
direction = ['D', 'R', 'U', 'L']
for i in range(4):
path.append(direction[i])
if solve_maze(maze, startX + dx[i], startY + dy[i], targetX, targetY, path):
return True
path.pop()
return FalseMaze
Given a maze and a start point and a target point, print out the path to reach the target.
Given a maze and a start point and a target point, return the path to reach the target.
Compare these 2, what is the difference?
When we share the field, what should we do?
Importance for backtracking -> keep the subproblem has the same state
Backtracking Summary
- Backtrack = try, iterate, traverse, etc.
- Keep trying (in the search space) until
- Solution is found
- No more meaningful methods to try (no more search space)
- Level-N problem -> M * Level-(N-1) subproblem
- Keep states the same when entering subproblem for shared fields.
Permutation (Leetcode 46)
Given a collection of distinct numbers, return all possible permutations.
For example,
[1,2,3] have the following permutations:
[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1].
public List<List<Integer>> permute(int[] nums) {
// Implement this method.
}
What is the time complexity?
O(n * n!)
Given a collection of distinct numbers, return all possible permutations.
public List<List<Integer>> permute(int[] num) {
List<List<Integer>> results = new ArrayList<List<Integer>>();
permute(results, new ArrayList<Integer>(), num);
return results;
}
public void permute(List<List<Integer>> results,
ArrayList<Integer> cur, int[] num) {
if (cur.size() == num.length) {
results.add(new ArrayList<Integer>(cur));
return;
}
for (int i = 0; i < num.length; i++) {
if (cur.contains(num[i])) {
continue;
}
cur.add(num[i]);
permute(results, cur, num);
cur.remove(cur.size() - 1);
}
}Permutation (Leetcode 46)
Which part is not efficient? -> array contains
Given a collection of distinct numbers, return all possible permutations.
Permutation (Leetcode 46)
Which part is not efficient? -> array contains
def permute(num):
results = []
permute_helper(results, [], num)
return results
def permute_helper(results, cur, num):
if len(cur) == len(num):
results.append(list(cur))
return
for i in num:
if i in cur:
continue
cur.append(i)
permute_helper(results, cur, num)
cur.pop()
public ArrayList<ArrayList<Integer>> permute(int[] num) {
ArrayList<Integer> numList = new ArrayList<Integer>();
for (int i = 0; i < num.length; i++)
numList.add(num[i]);
return permute(new ArrayList<Integer>(), numList);
}
public ArrayList<ArrayList<Integer>> permute(ArrayList<Integer> cur,
ArrayList<Integer> num) {
ArrayList<ArrayList<Integer>> results =
new ArrayList<ArrayList<Integer>>();
if (num.size() == 0) {
results.add(cur);
return results;
}
for (int i = 0; i < num.size(); i++) {
ArrayList<Integer> newCur = new ArrayList<Integer>(cur);
newCur.add(num.get(i));
ArrayList<Integer> newNum = new ArrayList<Integer>(num);
newNum.remove(i);
results.addAll(permute(newCur, newNum));
}
return results;
}Permutation (Leetcode 46)
What part is not efficient?
copy the array takes time
Permutation (Leetcode 46)
def permute(num):
num_list = list(num)
return permute_helper([], num_list)
def permute_helper(cur, num):
results = []
if len(num) == 0:
results.append(cur)
return results
for i in range(len(num)):
new_cur = cur + [num[i]]
new_num = num[:i] + num[i+1:]
results.extend(permute_helper(new_cur, new_num))
return results
Permutation (Leetcode 46)
How to debug and learn from other solution
def permute(num):
num_list = list(num)
return permute_helper([], num_list)
def permute_helper(cur, num):
print(cur, num)
results = []
if len(num) == 0:
results.append(cur)
return results
for i in range(len(num)):
new_cur = cur + [num[i]]
new_num = num[:i] + num[i+1:]
results.extend(permute_helper(new_cur, new_num))
return results
([], [2, 6, 8])
([2], [6, 8])
([2, 6], [8])
([2, 6, 8], [])
([2, 8], [6])
([2, 8, 6], [])
([6], [2, 8])
([6, 2], [8])
([6, 2, 8], [])
([6, 8], [2])
([6, 8, 2], [])
([8], [2, 6])
([8, 2], [6])
([8, 2, 6], [])
([8, 6], [2])
([8, 6, 2], [])
Permutation II (Leetcode 47)
Given a collection of distinct numbers, return all possible permutations.
public List<List<Integer>> permuteUnique(int[] num) {
List<List<Integer>> results = new ArrayList<List<Integer>>();
Arrays.sort(num);
boolean[] visited = new boolean[num.length];
for (int i = 0; i < visited.length; i++) {
visited[i] = false;
}
permute(results, new ArrayList<Integer>(), num, visited);
return results;
}
public void permute(List<List<Integer>> results, List<Integer> cur, int[] num, boolean[] visited) {
if (cur.size() == num.length) {
results.add(new ArrayList<Integer>(cur));
return;
}
for (int i = 0; i < num.length; i++) {
if (visited[i] || (i > 0 && num[i] == num[i-1] && !visited[i-1])) {
continue;
}
visited[i] = true;
cur.add(num[i]);
permute(results, cur, num, visited);
cur.remove(cur.size() - 1);
visited[i] = false;
}
return;
}Permutation II (Leetcode 47)
Given a collection of distinct numbers, return all possible permutations.
def permuteUnique(num):
results = []
num.sort()
visited = [False] * len(num)
permute(results, [], num, visited)
return results
def permute(results, cur, num, visited):
if len(cur) == len(num):
results.append(list(cur))
return
for i in range(len(num)):
if visited[i] or (i > 0 and num[i] == num[i - 1] and not visited[i - 1]):
continue
visited[i] = True
cur.append(num[i])
permute(results, cur, num, visited)
cur.pop()
visited[i] = False
Permutation II (Leetcode 47)
Given a collection of distinct numbers, return all possible permutations.
public List<List<Integer>> permuteUnique(int[] num) {
List<List<Integer>> results = new ArrayList<List<Integer>>();
List<Integer> nums = new ArrayList<Integer>();
Arrays.sort(num);
for (int i = 0; i < num.length; i ++) {
nums.add(num[i]);
}
permute(results, nums, 0);
return results;
}
public void permute(List<List<Integer>> results, List<Integer> num, int index) {
if (index == num.size()) {
results.add(num);
return;
}
for (int i = index; i < num.size(); i++) {
if (i != index && num.get(index) == num.get(i)) continue;
swap(num, index, i);
permute(results, new ArrayList<Integer>(num), index + 1);
}
}
public void swap(List<Integer> num, int i, int j) {
int temp = num.get(i);
num.set(i, num.get(j));
num.set(j, temp);
}Permutation II (Leetcode 47)
Given a collection of distinct numbers, return all possible permutations.
def permuteUnique(self, nums):
results = []
num = sorted(nums)
self.permute(results, num, 0)
return results
def permute(self, results, num, index):
if index == len(num):
results.append(num[:])
return
for i in range(index, len(num)):
if i != index and num[index] == num[i]:
continue
num[index], num[i] = num[i], num[index]
self.permute(results, num[:], index + 1)Combination
Given a collection of distinct numbers, return all possible combinations.
For example,
[2, 6, 8] have the following powersets (combination):
[], [2], [6], [8], [2, 6], [2, 8], [6, 8], [2, 6, 8].
public List<List<Integer>> combine(int[] nums) {
// Implement this method.
}
Combination
Given a collection of distinct numbers, return all possible combinations.
public static List<List<Integer>> combine(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
combination(results, nums, 0, new ArrayList<Integer>());
return results;
}
public static void combination(List<List<Integer>> results,
int[] nums, int index, ArrayList<Integer> items) {
if (index == nums.length) {
results.add(items);
return;
}
ArrayList<Integer> newItems1 = new ArrayList<Integer>(items);
combination(results, nums, index+1, newItems1);
ArrayList<Integer> newItems2 = new ArrayList<Integer>(items);
newItems2.add(nums[index]);
combination(results, nums, index+1, newItems2);
}Combination
Given a collection of distinct numbers, return all possible combinations.
def combine(nums):
results = []
combination_helper(results, nums, 0, [])
return results
def combination_helper(results, nums, index, items):
if index == len(nums):
results.append(list(items))
return
combination_helper(results, nums, index + 1, items)
new_items = items + [nums[index]]
combination_helper(results, nums, index + 1, new_items)
Combination
Given a collection of distinct numbers, return all possible combinations.
public static List<List<Integer>> combine(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
combination(results, nums, 0, new ArrayList<Integer>());
return results;
}
public static void combination(List<List<Integer>> results,
int[] nums, int index, ArrayList<Integer> items) {
if (index == nums.length) {
results.add(new ArrayList<Integer>(items));
return;
}
combination(results, nums, index+1, items);
items.add(nums[index]);
combination(results, nums, index+1, items);
items.remove(items.size()-1);
}Combination
Given a collection of distinct numbers, return all possible combinations.
def combine(nums):
results = []
combination_helper(results, nums, 0, [])
return results
def combination_helper(results, nums, index, items):
if index == len(nums):
results.append(list(items))
return
combination_helper(results, nums, index + 1, items)
items.append(nums[index])
combination_helper(results, nums, index + 1, items)
items.pop()
Combination
Given a collection of distinct numbers, return all possible combinations.
public static List<List<Integer>> combine(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
combination(results, nums, 0, new ArrayList<Integer>());
return results;
}
public static void combination(List<List<Integer>> results,
int[] nums, int index,
ArrayList<Integer> items) {
if (index == nums.length) {
results.add(new ArrayList<Integer>(items));
return;
}
for (int i = index; i < nums.length; i++) {
items.add(nums[i]);
combination(results, nums, i+1, items);
items.remove(items.size()-1);
}
}The empty set is missing.
-There will be at least one element in the "items"
input: 2 6 8
output:
8
2,8
6,8
2,6,8
Combination
Given a collection of distinct numbers, return all possible combinations.
def combine(nums):
results = []
combination_helper(results, nums, 0, [])
return results
def combination_helper(results, nums, index, items):
results.append(list(items))
if index == len(nums):
return
for i in range(index, len(nums)):
items.append(nums[i])
combination_helper(results, nums, i + 1, items)
items.pop()
Combination
Given a collection of distinct numbers, return all possible combinations.
public List<List<Integer>> combine(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
combinationHelper(results, nums, 0, new ArrayList<>());
return results;
}
private void combinationHelper(List<List<Integer>> results, int[] nums, int index, List<Integer> items) {
results.add(new ArrayList<>(items));
if (index == nums.length) {
return;
}
for (int i = index; i < nums.length; i++) {
items.add(nums[i]);
combinationHelper(results, nums, i + 1, items);
items.remove(items.size() - 1);
}
}Lucky Numbers
888 is a lucky number. And for each American phone number, we can actually add some operators to make it become 888. For example:
phone number is 7765332111, you will have
7/7*65*3+3*21*11 = 888
776+5+3*32+11*1 = 888
...
We want to get a full list of all the operation equations that can get a certain lucky number. The interface will be
List<String> luckyNumbers(String num, int target)
Lucky Numbers
We want to get a full list of all the operation equations that can get a certain lucky number. The interface will be
List<String> luckyNumbers(String num, int target)
Additional information:
String num will always be 10 digits since it is a phone number.
we can have "0" but we cannot have "05", "032".
If a number cannot be divided, you cannot use it. For example, 55/2 is not allowed, you need to make sure the division can always be an integer result.
0 cannot be divided.
Lucky Numbers
We need to use recursion to solve the problem
Since we want to output the result. There are things we need to pay attention:
1. The first number does not have operators in front.
2. Use long in case you get the number overflow
3. * and / has higher priority than + and -. How do you handle that?
4. remind 0
Lucky Numbers
def lucky_numbers(num, target):
result = []
recursion(num, target, "", 0, 0, 0, result)
return result
def recursion(num, target, temp, pos, current, last, result):
if pos == len(num):
if current == target:
result.append(temp)
return
for i in range(pos, len(num)):
if num[pos] == '0' and i != pos:
break
m = num[pos:i + 1]
n = int(m)
if pos == 0:
recursion(num, target, temp + m, i + 1, n, n, result)
else:
recursion(num, target, temp + "+" + m, i + 1, current + n, n, result)
recursion(num, target, temp + "-" + m, i + 1, current - n, -n, result)
recursion(num, target, temp + "*" + m, i + 1, current - last + last * n, last * n, result)
if n != 0 and last % n == 0:
recursion(num, target, temp + "/" + m, i + 1, current - last + last // n, last // n, result)
Lucky Numbers
public List<String> luckyNumbers(String num, int target) {
List<String> result = new ArrayList<>();
recursion(num, target, "", 0, 0, 0, result);
return result;
}
public void recursion(String num, int target, String temp, int pos,
long current, long last, List<String> result) {
if (pos == num.length()) {
if (current == target) {
result.add(temp);
}
return;
}
for (int i = pos; i < num.length(); i ++) {
if (num.charAt(pos) == '0' && i != pos) break;
String m = num.substring(pos, i + 1);
long n = Long.valueOf(m);
if (pos == 0) {
recursion(num, target, temp + m, i + 1, n, n, result);
} else {
recursion(num, target, temp + "+" + m, i + 1, current + n, n, result);
recursion(num, target, temp + "-" + m, i + 1, current - n, -n, result);
recursion(num, target, temp + "*" + m, i + 1, current - last + last * n, last * n, result);
if (n != 0 && last % n == 0) {
recursion(num, target, temp + "/" + m, i + 1, current - last + last / n, last / n, result);
}
}
}
}Lucky Numbers
Example:
24 + 5 -> current 29, last 5
24 + 5 * 4 -> current 29 - 5 + 20 = 44, last 20
24 + 5 * 4 / 2 -> current 44 - 20 + 10 = 34, last 10
24 + 5 * 4 / 2 - 7 -> current 34 - 7 = 27, last -7
Knapsack
Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
All candidate numbers are unique.
The same repeated number may be chosen from C unlimited number of times.
Note:
- All numbers (including target) will be positive integers.
- Elements in a combination (a1, a2, … , ak) must be in non-descending order. (ie, a1 ≤ a2 ≤ … ≤ ak).
- The solution set must not contain duplicate combinations.
Example Input: [7], [2, 3, 6, 7]
Example Output: [[2, 2, 3], [7]]
Knapsack
Similar as the previous Knapsack, consider the subproblems
Define the problem as (C, i, T), then given a number
- Pick => (C, i, T-C[i])
- Not Pick => (C, i+1, T)
Why i does not move when we pick?
Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
All candidate numbers are unique.
The same repeated number may be chosen from C unlimited number of times.
Knapsack
public static ArrayList<ArrayList<Integer>> knapsack(int[] candidates,
int target) {
ArrayList<ArrayList<Integer>> results = new ArrayList<ArrayList<Integer>>();
ArrayList<Integer> cur = new ArrayList<Integer>();
knapsack(candidates, 0, target, results, cur);
return results;
}
public static void knapsack(int[] candidates, int index, int target,
ArrayList<ArrayList<Integer>> results,
ArrayList<Integer> cur) {
if (target < 0 || (target != 0 && index == candidates.length)) {
return;
}
if (target == 0) {
results.add(new ArrayList<Integer>(cur));
return;
}
cur.add(candidates[index]);
knapsack(candidates, index, target-candidates[index], results, cur);
cur.remove(cur.size()-1);
knapsack(candidates, index+1, target, results, cur);
}Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
why do we copy?
Knapsack
Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
def knapsack(candidates, target):
results = []
cur = []
knapsack_helper(candidates, 0, target, results, cur)
return results
def knapsack_helper(candidates, index, target, results, cur):
if target < 0 or (target != 0 and index == len(candidates)):
return
if target == 0:
results.append(cur[:])
return
cur.append(candidates[index])
knapsack_helper(candidates, index, target - candidates[index], results, cur)
cur.pop()
knapsack_helper(candidates, index + 1, target, results, cur)Knapsack
Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
All candidate numbers are unique.
The same repeated number may be chosen from C unlimited number of times.
Another way to solve the problem?
Recursion does not have to be one way to solve
Iterate all numbers to decide whether to pick the current number.
<=>
Which one of the numbers should I pick as the smallest one in the current set.
Knapsack
Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
public ArrayList<ArrayList<Integer>> knapsack(int[] candidates, int target) {
ArrayList<ArrayList<Integer>> results = new ArrayList<ArrayList<Integer>>();
ArrayList<Integer> cur = new ArrayList<Integer>();
knapsack(candidates, 0, target, results, cur);
return results;
}
public void knapsack(int[] candidates, int index, int target,
ArrayList<ArrayList<Integer>> results,
ArrayList<Integer> cur) {
if (target < 0) {
return;
}
if (target == 0) {
results.add(new ArrayList<Integer>(cur));
return;
}
for (int i = index; i < candidates.length; i++) {
cur.add(candidates[i]);
knapsack(candidates, i, target-candidates[i], results, cur);
cur.remove(cur.size()-1);
}
return;
}Knapsack
Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
def knapsack(candidates, target):
results = []
cur = []
knapsack_helper(candidates, 0, target, results, cur)
return results
def knapsack_helper(candidates, index, target, results, cur):
if target < 0:
return
if target == 0:
results.append(cur[:])
return
for i in range(index, len(candidates)):
cur.append(candidates[i])
knapsack_helper(candidates, i, target - candidates[i], results, cur)
cur.pop()
returnKnapsack II
Given a collection of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
Candidate numbers may contain duplicate.
Each number in C may only be used once in the combination.
Knapsack I
input: [2,3,7], 9 -> [[2,2,2,3],[2,7],[3,3,3]]
Knapsack II
input: [2,2,3,7], 9 -> [[2,7]]
Knapsack II
public List<List<Integer>> knapsack(int[] candidates, int target) {
Arrays.sort(candidates);
List<List<Integer>> results = new ArrayList<List<Integer>>();
List<Integer> cur = new ArrayList<Integer>();
knapsack(candidates, 0, target, results, cur);
return results;
}
public void knapsack(int[] candidates, int index, int target,
List<List<Integer>> results, List<Integer> cur) {
if (target < 0) return;
if (target == 0) {
results.add(new ArrayList<Integer>(cur));
return;
}
for (int i = index; i < candidates.length; i++) {
cur.add(candidates[i]);
knapsack(candidates, i+1, target-candidates[i], results, cur);
cur.remove(cur.size()-1);
while (i < candidates.length-1 && candidates[i] == candidates[i+1]) i++;
}
return;
}when it is used, need to use the next
Why do we need to skip?
-> avoid duplicate subproblem
Knapsack II
def knapsack(candidates, target):
candidates.sort()
results = []
cur = []
knapsack_helper(candidates, 0, target, results, cur)
return results
def knapsack_helper(candidates, index, target, results, cur):
if target < 0:
return
if target == 0:
results.append(cur[:])
return
for i in range(index, len(candidates)):
cur.append(candidates[i])
knapsack_helper(candidates, i + 1, target - candidates[i], results, cur)
cur.pop()
while i < len(candidates) - 1 and candidates[i] == candidates[i + 1]:
i += 1
return0-1 Knapsack II
Given a knapsack which can hold s pounds of items, and a set of items with weight w1, w2, ... wn. Try to put items into the pack as many as possible, return the largest weight we can get in the knapsack.
public int knapsack(int s, int[] weights) {
return knapsack(s, weights, 0);
}
public int knapsack(int s, int[] weights, int index) {
if (s == 0 || index == weights.length) {
return 0;
}
if (weights[index] > s) {
return knapsack(s, weights, index+1);
}
return Math.max(knapsack(s, weights, index+1),
weights[index] + knapsack(s-weights[index], weights, index+1));
}The subproblem's relationship has changed.
This is not the best solution, we can use Dynamic Programming
0-1 Knapsack II
Given a knapsack which can hold s pounds of items, and a set of items with weight w1, w2, ... wn. Try to put items into the pack as many as possible, return the largest weight we can get in the knapsack.
The subproblem's relationship has changed.
This is not the best solution, we can use Dynamic Programming
def knapsack(s, weights):
return knapsack_recursive(s, weights, 0)
def knapsack_recursive(s, weights, index):
if s == 0 or index == len(weights):
return 0
if weights[index] > s:
return knapsack_recursive(s, weights, index + 1)
return max(knapsack_recursive(s, weights, index + 1),
weights[index] + knapsack_recursive(s - weights[index], weights, index + 1))
0-1 Knapsack
Given a knapsack which can hold s pounds of items, and a set of items with weight w1, w2, ... wn. Return whether we can pick specific items so that their total weight s.
Example Input:
s = 20;
w = [14, 8, 7, 5, 3];
Example Output:
True; (8, 7, 5)
We need to think what are the sub problems
Given an item, just two options:
- pick it, the problem become (s-w[i], w - w[i])
- not pick it, the problem become (s, w - w[i])
0-1 Knapsack
Given a knapsack which can hold s pounds of items, and a set of items with weight w1, w2, ... wn. Return whether we can pick specific items so that their total weight s.
public boolean knapsack(int s, int[] weights) {
return knapsack(s, weights, 0);
}
public boolean knapsack(int s, int[] weights, int index) {
if (s == 0) {
return true;
}
if (s < 0 || index == weights.length) {
return false;
}
return knapsack(s - weights[index], weights, index+1) ||
knapsack(s, weights, index+1);
}add/remove elements in weights is hard --> add an index and move index
Consider the 2 return, does the order matter?
0-1 Knapsack
def knapsack(s, weights):
return knapsack_recursive(s, weights, 0)
def knapsack_recursive(s, weights, index):
if s == 0:
return True
if s < 0 or index == len(weights):
return False
return knapsack_recursive(s - weights[index], weights, index+1) or knapsack_recursive(s, weights, index+1)Summary
Recursion
subproblem
-> problem
subproblem-1 ||
subproblem-2 ||
subproblem-N
-> problem
subproblem-1 &&
subproblem-2 &&
subproblem-N
-> problem
Factorial,
Sum of LinkedList,
Remove Linked List Element, etc.
Maze,
Sudoku,
Most DFS problems, etc.
Knapsack
Permutations,
Combinations,
Eight Queen,
kSum, etc.
Summary
- Recursion is a strategy.
- Always try to split a problem into sub-problems and solve the sub-problem first.
- If the solution is the same, then you can call the same method.
Homework
Homework (Optional)
Homework (Optional)
Copy of [GoValley-Jo] Recursion 1
By ZhiTongGuiGu
Copy of [GoValley-Jo] Recursion 1
- 92



