圖論(二)
建國中學 陳仲肯
「meow」by蔡俊則
目錄
- 最小生成樹
- DFS TREEEEEEE
- 關節點
- 橋
- SCC
- Tarjan
- Kosaraju
- BCC(點)
- BCC(邊)
- 2-SAT
- 噁心的題目們
最小生成樹
MST Minimum Spanning Tree
定義
對於所有連通圖,點數與原圖相同、邊數最少的連通子圖
一定是一棵樹,稱為生成樹
邊權總和最小的生成樹即稱為最小生成樹
利用性質
一個連通圖內兩個未完成的最小生成樹
用最短的邊連接一定最好
Kruskal演算法
每次找當前權重最小的邊,
看端點是否在兩個不同的最小生成樹中,
是的話就把兩棵樹合併起來。
如何合併?
還記得並查集嗎?
複雜度
把所有邊排序,所有邊看過一次並查集
\(O(E log E)\)
struct E{int u,v,w;};
bool cmp(E a,E b){return a.w<b.w;}
E edge[N];
int Kruskal(){
sort(edge, edge+m, cmp);
int ans=0;
for(int i=0;i<m;i++){
if(fa(edge[i].u)!=fa(edge[i].v)){
ans+=edge[i].w;
join(edge[i].u, edge[i].v);
}
}
return ans;
}Prim's Algorithm
跟Dijkstra類似
把「與原點距離」改成「與樹距離」
複雜度
pq的話跟dijkstra滿像的,每條邊push一次,對每個點pop一次
- priority queue:\(O((E+V)log V)\)
- 用矩陣存:\(O(V^2)\)
struct E{int v,w;};
struct cmp{bool operator()(E a,E b){return a.w>b.w;}};
priority_queue<E,vector<E>,cmp> pq;
pq.push({1,0});
int ans=0;
dis[1]=0;//到樹距離
while(!pq.empty()){
E cur=pq.top();pq.pop();
if(vis[cur.v])continue;
vis[cur.v]=1;
ans+=cur.w;
for(auto [v,w]:G[cur.v]){
if(!vis[v]&&dis[v]>w){
dis[v]=w;
pq.push({v,w});
}
}
}
耍笨
我在寫Dijkstra時被Prim混淆,以為是存到樹距離
題目:TIOJ 1211
裸題
最小比率生成樹
每條邊有a,b兩種權重,求生成樹中\(\frac{\sum{a}}{\sum{b}}\)最小的
好像不能直接做?
解法
二分搜可以湊出來的最小比率!
如果我希望有一棵生成樹\(\frac{\sum{a}}{\sum{b}}<r\)
則\(\sum{a}-r\sum{b}<0\)
把每個邊的邊權設為\(a-rb\)
找最小生成樹,如果總和<0就可以
複雜度
做\(O(logC)\)次MST
C是\(值域\div精度\)
\(O((E+V)logElogC)\)
或\(O(ElogElogC)\)
DFS Tree
- Tree edge: 走到兒子的邊
- Back edge: 走到祖先的邊
- Forward edge: 走到非兒子的子孫的邊
- Cross edge: 走到非直系血親的邊

邊的種類
whut it look like


關節點
for無向圖

我是沉重肯醫師, 我信賴普拿疼
圖的膝蓋,拔掉會使圖不連通的點

定義
如何找關節點
Tarjan
讀作:塔樣
DFS TREEEEEEE


無向圖的DFS TREEEEEEE
Tarjan的想法
對於一個不是根點的u,有任何一個小孩子樹裡所有back edge的終點都在u的子樹裡,則u是關節點
對於根點,如果dfs tree 上小孩個數>=2
就是關節點
e.g. 賴賴跟Wiwi有兩個小孩(小賴跟小Wi)
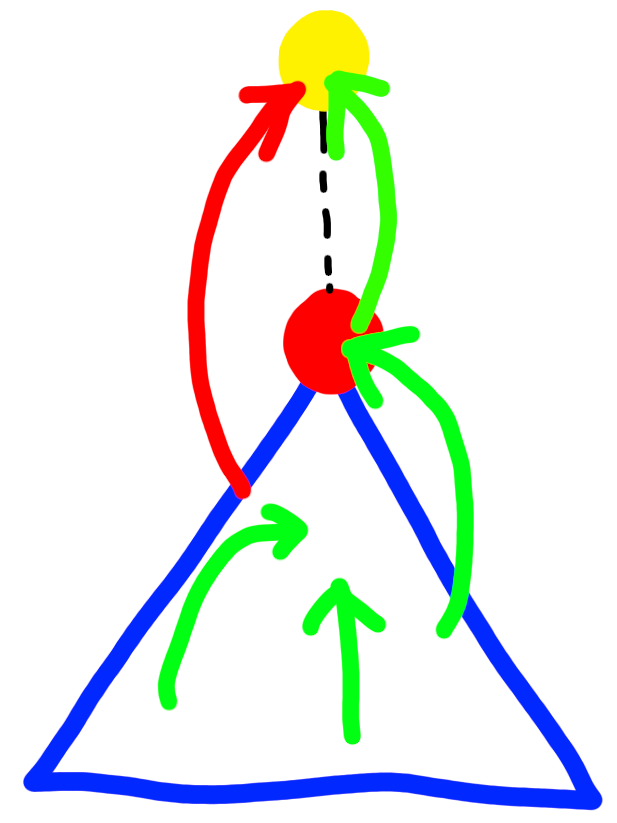
u
u的祖先
找關節點?
\(low_i:=i\)的子樹中的back edge的\(dfs\)序最小值
int cnt=0;
int low[N],in[N];
vector<int> G[N];
void dfstreeeeee(int u,int fa=-1){
low[u]=in[u]=++cnt;
int child=0;
for(int v:G[u]){
if(v==fa)continue;
if(in[v])low[u]=min(low[u],in[v]);//u到v是back edge
else{
dfstreeeeee(v,u);
if(fa!=-1&&low[v]>=in[u])IS_CUTPOINT(u);//u把v和fa分開
++child;low[u]=min(low[u],low[v]);
}
}
if(fa==-1&&child>1)IS_CUTPOINT(u);
}橋
for無向圖


橋?
橋牌?

定義
拔掉會使圖不連通的邊
如何找橋
Tarjan
讀作:塔樣
DFS TREEEEEEE

小性質

Back edge不會是橋
看Tree edge就好
Tarjan的想法
對於一個點u如果他兒子v的子樹裡所有 back edge的終點都在子樹裡
則u--v是bridge

u
u的兒子
找橋?
\(low_i:=i\)的子樹中的back edge的\(dfs\)序最小值
int cnt=0;
int low[N],in[N];
vector<int> G[N];
void dfstreeeeee(int u,int fa=-1){
low[u]=in[u]=++cnt;
int child=0;
for(int v:G[u]){
if(v==fa)continue;
if(in[v])low[u]=min(low[u],in[v]);//u到v是back edge
else{
dfstreeeeee(v,u);
low[u]=min(low[u],low[v]);
if(low[v]==in[v])IS_BRIDGE(u,v);
}
}
}如何描述有向圖的連通狀況?
弱連通、強連通
這兩個名詞都只適用於有向圖
- 弱連通:
- 把邊都改成無向邊後連通
- 對於每個點對\(u,v\)存在\(u\to v\)或\(v\to u\)
- 強連通:對於每個點對\(u,v\)存在\(u\to v\)和\(v\to u\)


this is SCC
this is not SCC
Tarjan
讀作:塔樣
DFS TREEEEEEE

作法
如果一個點的子樹經過back edge最高都只能到他自己則他是SCC的頭

詳細作法
開一個stack,存現在有可能在SCC的點
DFS時,看完相鄰的點,如果low[u]==in[u],則stack中直到自己的點都在同一個SCC,pop掉
每個點只會在一個SCC中,所以在最高點處理沒問題
遇到四種邊會怎樣?
- Tree edge: vis=0繼續DFS,用low更新low值
- Back edge: vis=1,inStack,用vis更新low值
- Forward edge:vis=1,inStack or !inStack,反正看過了,沒差
- Cross edge: vis=1,!inStack的話不做事,inStack的話用vis更新low值
void dfs(int u){
low[u]=in[u]=cnt++;
stk.push(u);
for(int v:G[u]){
if(!vis[v]){
dfs(v);
low[u]=min(low[u],low[v]);
}else if(!scc[v]){
low[u]=min(low[u],in[v]);
}
}
if(low[u]==in[u]){
int cur;
do{
cur=stk.top();stk.pop();
scc[cur]=scctot;
}while(cur!=u);
++scctot;
}
}縮點?
把每個SCC當作一個點,邊照連


縮點完會是DAG(有向無環圖)
PROOF:有環的話就應該要縮起來
力提
需要一點巧思
多設一個點0,代表任何點
有傳送站的可以到0
0可以到任何點
然後就跟上一題一樣了
Kosaraju
另一個找SCC的演算法
Kosaraju!

作法
做一次DFS,紀錄離開節點的順序
從後離開的開始對反向圖再DFS一次,能到的點就在同一個SCC
圖例

正確性
考慮u,v間的路徑
- u--->v 且 v--->u 不管正的誰先,反的一定能走到
- u-x->v 且 v-x->u顯然不會放在同SCC(反的走不到)
- u--->v 且 v-x->u 反圖(u-x->v 且 v--->u)DFS一定要先看u,而正的不可能先離開u,因為一定會先離開v或本來就在v後面



建反向邊

DFS, 紀錄出來順序
void dfs(int u){
if(vis[u])return;
vis[u]=1;
for(int v:G[u])dfs(u);
out.push(u)
}照出來順序對反向圖DFS, 能走到的都在同一個SCC
void bfs(int u){
if(scc[u])return;
scc[u]=cnt;
for(int v:R[u])bfs(v);
}然後就做完了耶
好像其實超好寫

但Tarjan常數比較小?
完整版的扣
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
int cnt=0;
const int N=1e5+10;
bool vis[N];
int scc[N];
vector<int> G[N],R[N];
stack<int> out;
void bfs(int u){
if(vis[u])return;
vis[u]=1;
for(int v:R[u])bfs(v);
out.push(u);
}
void dfs(int u){
if(scc[u])return;
scc[u]=cnt;
for(int v:G[u])dfs(v);
}
int main(){
int n,m,a,b,u;
cin>>n>>m;
while(m--){
cin>>a>>b;
G[a].pb(b);
R[b].pb(a);
}
for(int i=1;i<=n;i++)bfs(i);
while(!out.empty()){
u=out.top();
out.pop();
if(scc[u])continue;
cnt++;
dfs(u);
}
cout<<cnt<<"\n";
for(int i=1;i<=n;i++){
cout<<scc[i]<<" ";
}
return 0;
}
力提
扣
就上面那個啊
by謝一
TIOJ 1451
八卦傳播系統
扣(謝一:「我以前的扣居然長這樣?!」)
#include <bits/stdc++.h>
using namespace std;
int cnt, sccn, scc[100010];
bool vis[100010], in[100010];
pair<int, int> past[100010];
vector<int> road[100010];
vector<int> backway[100010];
void dfsb(int now){
past[now].second = now;
vis[now] = true;
for(int i = 0; i < backway[now].size(); i++){
if(!vis[backway[now][i]]) dfsb(backway[now][i]);
}
past[now].first = cnt;
cnt++;
}
void dfs(int now){
vis[now] = true;
scc[now] = sccn;
for(int i = 0; i < road[now].size(); i++){
if(!vis[road[now][i]]){
dfs(road[now][i]);
}
}
}
int main(){
int n, m, a, b, ans;
cin >> n >> m;
past[0] = {0, 0};
ans = 0;
for(int i = 1; i <= n; i++){
road[i].clear();
backway[i].clear();
vis[i] = false;
}
for(int i = 0; i < m; i++){
cin >> a >> b;
road[a].push_back(b);
backway[b].push_back(a);
}
cnt = 1;
for(int i = 1; i <= n; i++){
if(!vis[i]) dfsb(i);
}
sort(past + 1, past + n + 1);
memset(vis, false, n + 1);
sccn = 0;
for(int i = n; i > 0; i--){
if(!vis[past[i].second]){
dfs(past[i].second);
sccn++;
}
}
memset(in, true, sccn);
for(int i = 1; i <= n; i++){
for(int j = 0; j < road[i].size(); j++){
if(scc[road[i][j]] != scc[i]) in[scc[road[i][j]]] = false;
}
}
for(int i = 0; i < sccn; i++){
if(in[i]) ans++;
}
cout << ans << "\n";
return 0;
}點雙連通分量(BCC)
不存在關節點的連通分量
Tarjan
讀作:塔樣
DFS TREEEEEEE

一個點可能在多個BCC中
但一條邊一定會且只會在一個BCC中

點雙連通分量可以把邊分群!

怎麼找?
用找關節點的方法+紀錄SCC的方法
找到時把stack裡的pop掉
記得考慮關節點
實作
int low[N],tin[N],id[N],t,cnt;
vector<int> bcc[N],G[N];
stack<int> s;
void dfs(int u,int p=0){
low[u]=tin[u]=++t;
s.push(u);
for(int v:G[u])if(v!=p){
if(tin[v])low[u]=min(low[u],tin[v]);
else{
dfs(v,u);
if(low[v]>=tin[u]){
cnt++;
int k;
do{
k=s.top();s.pop();
bcc[k].pb(cnt);
}while(k!=v);
bcc[u].pb(cnt);
}
low[u]=min(low[u],low[v]);
}
}
}
bool iscut[N];
vector<int> T[N];
void build(){
dfs(1);
for(int i=1;i<=n;i++){
if(bcc[i].size()>1){
id[i]=++cnt;
iscut[id[i]]=true;
for(int j:bcc[i]){
T[id[i]].PB(j);
T[j].PB(id[i]);
}
}else{
id[i]=bcc[i][0];
}
}
}
如果一個點被多個BCC覆蓋,那他是關節點
Block-cut tree
把每個BCC縮點,中間用關節點連起來

對於有些問題,於把圖的問題變成樹的問題會大大簡化問題
以上我一題都沒寫過
我弱,對不起
橋雙連通分量(也是BCC)
不存在橋的連通分量
Tarjan
讀作:塔樣
DFS TREEEEEEE

跟點的大致雷同

邊不一定都在BCC中
但一條點一定會且只會在一個BCC中
點BCC是把邊分群
邊BCC是把點分群
void dfs(int u,int be=-1){//be: edge from last vertex
++cnt;
vis[u]=low[u]=cnt;
stk.push(u);
for(int e:G[u]){
if(e==be)continue;
int v=E[e];
if(!vis[v]){
dfs(v,e^1);
low[u]=min(low[u],low[v]);
if(low[v]>vis[u]){//u-v is bridge
++bcctot;
int cur;
do{
cur=stk.top();stk.pop();
bcc[bcctot].pb(cur);
}while(cur!=v);
}
}
else if(vis[v]<vis[u])low[u]=min(low[u],low[v]);
}
}扣
要仔細判斷重邊
縮點
一定會是樹(沒有環)

對於有些問題,於把圖的問題變成樹的問題會大大簡化問題
以上我一樣一題都沒寫過
我弱,對不起
2-SAT
不知道講不講得到這裡
你想找到有沒有解
建圖

如何判斷
看 \(x\) 跟 \(-x\) 是不是在同一個 \(SCC\) 裡面就好了
構解
拓樸排序 從後面開始選
扣
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=1e5+10;
int cnt=0;
bool ans[N],vis[2*N];
int scc[2*N],in[2*N];
vector<int> G[2*N],R[2*N],S[2*N],C[2*N];
stack<int> out,ord;
void bfs(int u){
if(vis[u])return;
vis[u]=1;
for(int v:R[u])bfs(v);
out.push(u);
}
void dfs(int u){
if(scc[u])return;
scc[u]=cnt;
for(int v:G[u])dfs(v);
}
void topological_sort(int n){
int u;
bool ok;
queue<int> Q;
for(int i=1;i<=cnt;i++){
if(!in[i])Q.push(i);
}
while(!Q.empty()){
u=Q.front();
Q.pop();
ord.push(u);
for(int v:S[u]){
in[v]--;
if(!in[v])Q.push(v);
}
}
while(!ord.empty()){
u=ord.top();
ord.pop();
ok=1;
for(int v:C[u]){
if(vis[v/2])ok=0;
}
if(!ok)continue;
for(int v:C[u]){
ans[v/2]=v&1;
vis[v/2]=1;
}
}
}
signed main(){
int n,m,a,b,u;
char wa,wb;
cin>>m>>n;
while(m--){
cin>>wa>>a>>wb>>b;
a<<=1,b<<=1;
if(wa=='+')a++;
if(wb=='+')b++;
G[a^1].pb(b);
G[b^1].pb(a);
R[b].pb(a^1);
R[a].pb(b^1);
}
for(int i=2;i<=2*n+1;i++){
bfs(i);
}
while(!out.empty()){
u=out.top();
out.pop();
if(!scc[u])cnt++;
dfs(u);
}
for(int i=1;i<=n;i++){
if(scc[2*i]==scc[2*i+1]){
cout<<"IMPOSSIBLE";
return 0;
}
}
for(int i=2;i<=2*n+1;i++){
C[scc[i]].pb(i);
for(int v:G[i]){
if(scc[v]==scc[i])continue;
S[scc[i]].pb(scc[v]);
in[scc[v]]++;
}
vis[i/2]=0;
}
topological_sort(n);
for(int i=1;i<=n;i++){
cout<<(ans[i]?"+":"-");
}
return 0;
}
力提
扣
就上面那個啊
課後問題: 想一下3-SAT怎麼做
抄來的一大堆題
劉澈給的題目都不是圖論的...
圖論(二)(資讀)
By kennyfs
圖論(二)(資讀)
我不會圖論所以我才來教圖論
- 929



