SCC和BCC
無向圖的割頂、關節點
(articulation point)
一個圖中,拔掉一個節點(和與其相連的邊)之後,若此圖變得不連通,則該節點為關節點
怎麼找?
DFS一次!
DFS TREE
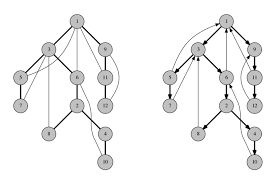
無向圖只有tree edge和back edge喔!
low值:DFS TREE 中以某個節點為根的子樹,透過走最多一條back edge能走到的最小前序編號。
Tarjan:
int cnt = 0;
vector<int> G[MAXN];
int pre[MAXN],low[MAXN];
void DFS(int u,int p)
{
low[u] = pre[u] = ++cnt;
for(auto v : G[u])
{
if(!pre[v])
{
DFS(v,u);
low[u] = min(low[u],low[v]);
}
else if(pre[v] < pre[u] && v != fa)
{
low[u] = min(low[u],pre[v]);
}
}
}int cnt = 0;
vector<int> G[MAXN];
int pre[MAXN],low[MAXN],iscut[MAXN];
void DFS(int u,int p)
{
low[u] = pre[u] = ++cnt;
int child = 0;
for(auto v : G[u])
{
if(!pre[v])
{
child ++;
DFS(v,u);
low[u] = min(low[u],low[v]);
if(low[v] >= pre[u])
{
iscut[u] = 1;
}
}
else if(pre[v] < pre[u] && v != p)
{
low[u] = min(low[u],pre[v]);
}
}
if(p <= 0 && child == 1)
{
iscut[u] = 0;
}
}無向圖的橋
(bridge)
一個圖中,拔掉一條邊之後,若此圖變得不連通,則該邊為橋。
如何做?
一樣low值
int cnt = 0;
vector<int> G[MAXN],isbridge[MAXN];
int pre[MAXN],low[MAXN],iscut[MAXN];
void DFS(int u,int p)
{
low[u] = pre[u] = ++cnt;
int child = 0;
for(int i = 0;i < G[u].size();i++)
{
int v = G[u][i];
if(!pre[v])
{
child ++;
DFS(v,u);
low[u] = min(low[u],low[v]);
if(low[v] > pre[u])
{
isbridge[u][i] = 1;
}
}
else if(pre[v] < pre[u] && v != p)
{
low[u] = min(low[u],pre[v]);
}
}
}一張圖邊雙聯通的極大子圖
邊雙聯通
不存在橋
一個節點只屬於一個邊雙聯通分量
邊雙聯通分量之間以橋隔開
DFS不走橋就好了
(code懶得附)
一張圖點雙聯通的極大子圖
點雙聯通
不存在關節點
一條邊只屬於一個點雙聯通分量
點雙聯通分量之間以關節點隔開
怎麼做?
先講完?
一張圖強連通的極大子圖
強聯通
每個點都走的到其他所有點
一個點只屬於一個SCC
怎麼做?
把原圖的所有邊倒過來,在新圖上DFS,紀錄離開順序。在原圖上以所紀錄之離開順序之反序做DFS,每次走到的節點即屬於該SCC。
證明?
XCC有啥用?
縮爆
無向圖縮成B(edge biconnected)CC會變成一棵樹(沒有環)
無向圖縮成SCC會變成一個DAG(沒有環)
點雙連通分量怎麼縮?
差不多了?
食祚
希望接下來有趣一點?
練習製造完美
deck
By Zi-Hong Xiao
deck
- 1,546



