Politics through the Lens of Economics
Lecture 4: Citizen-candidate Model
Masayuki Kudamatsu
25 October, 2017
Did everyone pick a policy?
For your term paper...
Start thinking (or even writing)
about whether
the Median Voter Theorem
can explain the failure to adopt
the policy of your choice
For your term paper...
Take note of the source of information

Image source: xkcd.com/285/
For your term paper...
& follow Harvard referencing
Discussion Time
Does the Median Voter Theorem explain
why voting is not compulsory in Japan?
Remember when a model can explain reality?
Source: CIA World Factbook (for data), www.pri.org/stories/2014-10-14/map-shows-all-countries-where-voting-mandatory (for image)
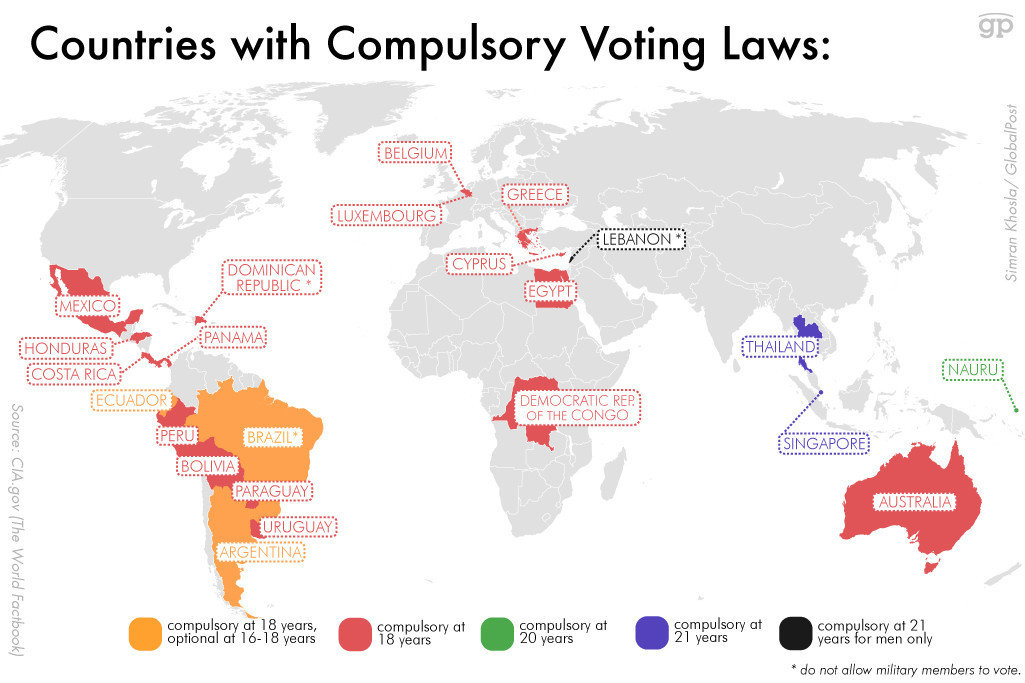
Background for discussion
Arguments in favor of compulsory voting
Source: Wikipedia
Higher legitimacy of the elected goverment
Exclusion of other voters cannot be the best strategy for politicians
Background for discussion
Waleed Aly (political scientist)
Make citizens learn about politics
Less money spent in elections
Reduce the influence of external factors such as weather and transport
Arguments against compulsory voting
Source: Wikipedia
Infringement of freedom of speech
Uninformed voters may become decisive
Background for discussion
Discussion Time
Does the Median Voter Theorem explain
why voting is not compulsory in Japan?
Remember
your aim is
to come up with
a wrong answer


Today's Road Map
Citizen-candidate Model
Testing the commitment assumption

Today's Economics Lessons
Citizen-candidate Model
Testing the commitment assumption
Multiple Equilibria
Regression Discontinuity Design

Today's Road Map
Citizen-candidate Model
Testing the commitment assumption
Motivations
Two restrictive assumptions
in the Median Voter Theorem
1. Commitment to electoral promise by politicians
2. Only two candidates compete in election
Citizen-candidate model
Assumes no commitment
Analyzes a citizen's decision to become a candidate
Consider a model of the world where
Step 1: Each citizen decides whether to run for office

Image source: www.city.hachioji.tokyo.jp/faq/27680/027703.html
Citizen-Candidate Model
Running for office is costly
Image source: www.city.hachioji.tokyo.jp/faq/27680/027703.html
Consider a model of the world where
Citizen-Candidate Model
Step 2: Each citizen decides whom to vote
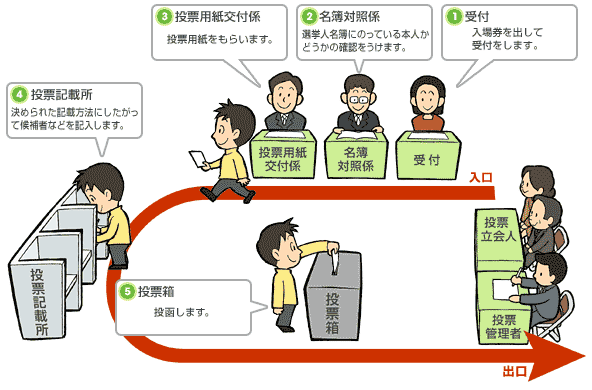
Image source: www.town.nogi.lg.jp/page/page000208.html
Consider a model of the world where
Citizen-Candidate Model
Candidate wins by plurality
Consider a model of the world where
Citizen-Candidate Model
Step 3: Winning candidate picks a policy to implement

Image source: saigaijyouhou.com/blog-entry-1098.html
Consider a model of the world where
Citizen-Candidate Model
Step 3: Winning candidate picks a policy to implement
Step 2: Each citizen decides whom to vote
Step 1: Each citizen decides whether to run for office
Running for office is costly
Candidate wins by plurarity
Consider a model of the world where
Citizen-Candidate Model
Let's consider optimization at each step
Step 3: Winning candidate picks a policy to implement
Step 2: Each citizen decides whom to vote
Step 1: Each citizen decides whether to run for office
Running for office is costly
Candidate wins by plurarity
Winning candidate's optimization in step 3:
Pick his/her own ideal policy
Image source: sayuflatmound.com/?p=19482

Let's consider optimization at each step
Step 3: Winning candidate picks a policy to implement
Step 2: Each citizen decides whom to vote
Step 1: Each citizen decides whether to run for office
Running for office is costly
Candidate wins by plurarity
Citizen's optimization in step 2 (voting):
Vote the candidate whose ideal policy is closest
unless there are three or more candidates (we see this later)
Remember Lecture 2 ?
Let's consider optimization at each step
Step 3: Winning candidate picks a policy to implement
Step 2: Each citizen decides whom to vote
Step 1: Each citizen decides whether to run for office
Running for office is costly
Candidate wins by plurarity
Citizen's optimization in step 1 (running for office):
Depends on
who else is running for office
Use the concept of equilibrium in such a case
In an equilibrium:
Each candidate
wants to run for office
No other citizen
wants to run for office
Each candidate
wants to run for office
No other citizen
wants to run for office
We now check whether these two equilibrium conditions hold when:
One candidate runs unopposed
Two candidates compete
One candidate runs unopposed
Each candidate
wants to run for office
No other citizen
wants to run for office
If the only candidate's ideal policy is not median
A citizen whose ideal policy is closer to median can win
Each candidate
wants to run for office
No other citizen
wants to run for office
If the only candidate's ideal policy is median
Median candidate can win and implement his/her ideal policy
One candidate runs unopposed
Each candidate
wants to run for office
No other citizen
wants to run for office
If the only candidate's ideal policy is median
Any non-median citizen cannot win
Another median citizen doesn't have to run to implement median policy
One candidate runs unopposed
One-candidate equilibrium
The same prediction as the Median Voter Theorem
runs for office
wins the election
implements the median policy
One median citizen
It does happen in reality that one candidate runs unopposed
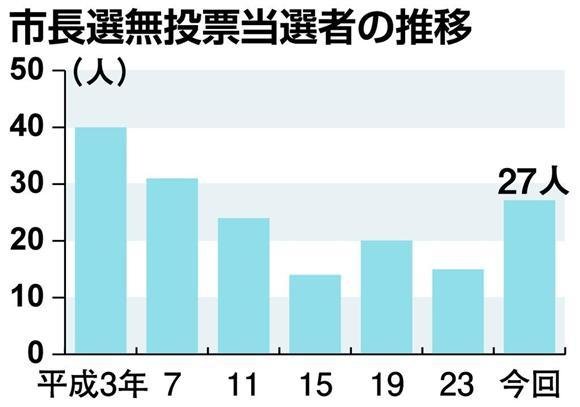
27
Two candidates compete
Each candidate
wants to run for office
No other citizen
wants to run for office
If each candidate's ideal policy is not symmetrical around median
The candidate farther away from median cannot win
Each candidate
wants to run for office
No other citizen
wants to run for office
If each candidate's ideal policy is symmetrical around median
Each candidate faces a 50% chance of winning
Two candidates compete
Each candidate
wants to run for office
No other citizen
wants to run for office
If each candidate's ideal policy is symmetrical around median
No other citizen
can win
(not even median voter)
Two candidates compete
Why can't any other other citizen win (not even median voter) ?
Policy
Median
A
B
Vote for A
Vote for B
With symmetrical two candidates
each citizen votes for who's closer
Policy
A
B
Vote for A
Vote for B
C
Why can't any other other citizen win (not even median voter) ?
Median
Suppose C decides to run for office
Policy
A
B
Vote for A
Vote for B
C
Switch to vote for C ?
Why can't any other other citizen win (not even median voter) ?
Median
Does any citizen closest to C switch to vote for C?
Policy
Median
A
B
Vote for A
Vote for B
C
When every other citizen votes for either A or B,
Those closer to A:
Switching to vote for C makes B win
Vote for C
That's worse than both A and B have a 50% winning chance
Policy
Median
A
B
Vote for A
Vote for B
C
When every other citizen votes for either A or B,
Those closer to B:
Switching to vote for C makes A win
Vote for C
That's worse than both A and B have a 50% winning chance
Policy
Median
A
B
Vote for A
Vote for B
C
When every other citizen votes for either A or B,
Same is true even if candidate C is median
Vote for C
Policy
Median
A
B
Vote for A
Vote for B
C
So C cannot win any vote
(even if C is median)
Policy
Median
A
B
Vote for A
Vote for B
C
With three or more candidates,
citizens may not vote for the candidate whose ideal policy is closest
(called "strategic voting")
Policy
Median
A
B
Vote for A
Vote for B
Since C cannot win any vote
(even if C is median)
C doesn't want to run for office
Each candidate
wants to run for office
No other citizen
wants to run for office
If each candidate's ideal policy is symmetrical around median
No other citizen
can win
(not even median voter)
Two candidates compete
A different prediction from the Median Voter Theorem
Two-candidate equilibrium
Two citizens whose ideal policy is symmetric around median
runs for office
wins the election with a 50% chance
Winning candidate
implements his/her ideal policy
Citizen-candidate model can explain the two-party system

image source: www.vice.com/read/the-first-presidential-debate-decoded
Three or more candidate equilibria
Possible, but too technical to discuss
Multiple equilibria
A
B
A
B
Policy
A
Median
A
B
Today's economics lesson #1
Citizen-candidate model has many equilibria
Multiple equilibria
A
B
A
B
Policy
A
Median
A
B
Today's economics lesson #1
We cannot predict which equilibrium to emerge in reality
Osaka
Tokyo

Image source: www.nikkei.com/article/DGXLASIH02H08_T01C14A2AA1P00/

Today's economics lesson #1
Multiple equilibria
We cannot predict which equilibrium to emerge in reality
Osaka
Tokyo

Image source: www.nikkei.com/article/DGXLASIH02H08_T01C14A2AA1P00/

Today's economics lesson #1
Multiple equilibria
Once an equilibrium is achieved, it's difficult to move to another
Today's economics lesson #1
A model with multiple equilibria:
Cannot be tested against the data
Multiple equilibria
Theoretically insightful
But we can check if the model assumption is consistent with data

Today's Road Map
Citizen-candidate Model
Testing the commitment assumption
Crucial in the citizen-candidate model
cannot commit to electoral promise
choose their own ideal policy once elected
Politicians
Lots of anecdotes supporting this assumption
But does it stand against more systematic evidence?
The no-commitment assumption
Ideal experiment
For randomly picked half
of electoral districts
For the remaining half
Median voter's ideal policy: similar on average
Ideal experiment
For randomly picked half
of electoral districts
Let Party A's candidate win
For the remaining half
Let Party B's candidate win
Median voter's ideal policy: similar on average
Ideal experiment
For randomly picked half
of electoral districts
Let Party A's candidate win
For the remaining half
Let Party B's candidate win
Median voter's ideal policy: similar on average
Winner's chosen policy: similar on average
if politicians can commit to electoral promise
Ideal experiment
For randomly picked half
of electoral districts
Let Party A's candidate win
For the remaining half
Let Party B's candidate win
Median voter's ideal policy: similar on average
if politicians cannot commit to electoral promise
A's ideal policy chosen
B's ideal policy chosen
Ideal experiment
For randomly picked half
of electoral districts
Let Party A's candidate win
For the remaining half
Let Party B's candidate win
Median voter's ideal policy: similar on average
But this is impossible!
Ideal experiment
For randomly picked half
of electoral districts
Let Party A's candidate win
For the remaining half
Let Party B's candidate win
Median voter's ideal policy: similar on average
Where does something similar to this
happen in reality?
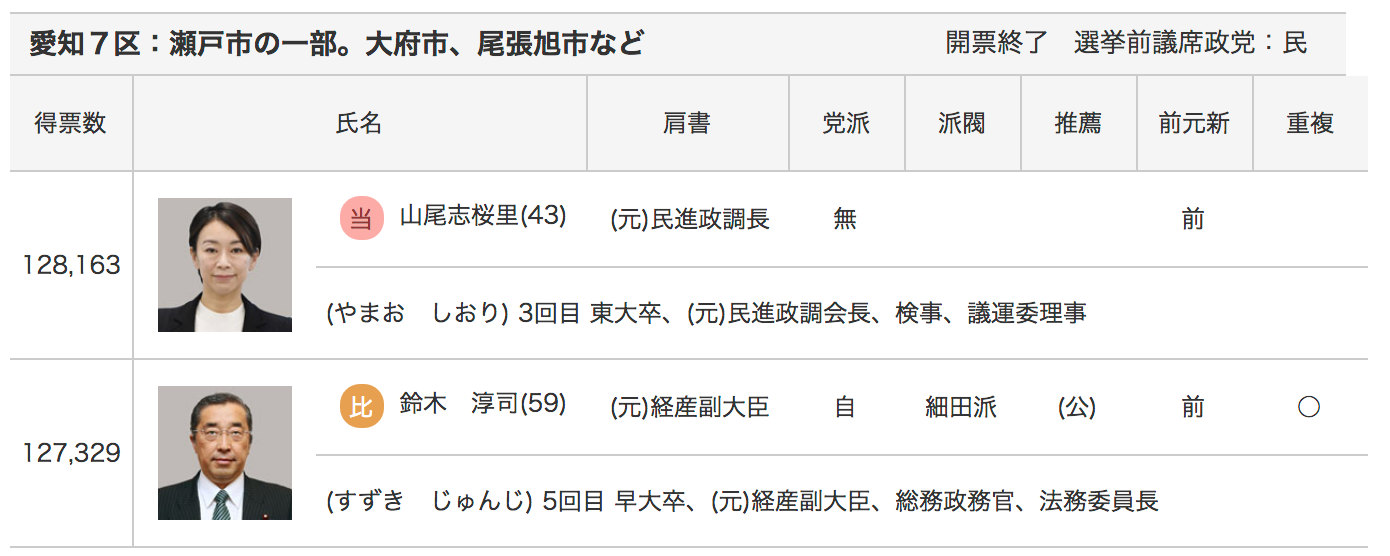
e.g. Aichi 7th district at the 2017 Lower House Election in Japan
Image source: https://www.nikkei.com/2017shuin/kaihyo/pref/?pref=23
Close elections

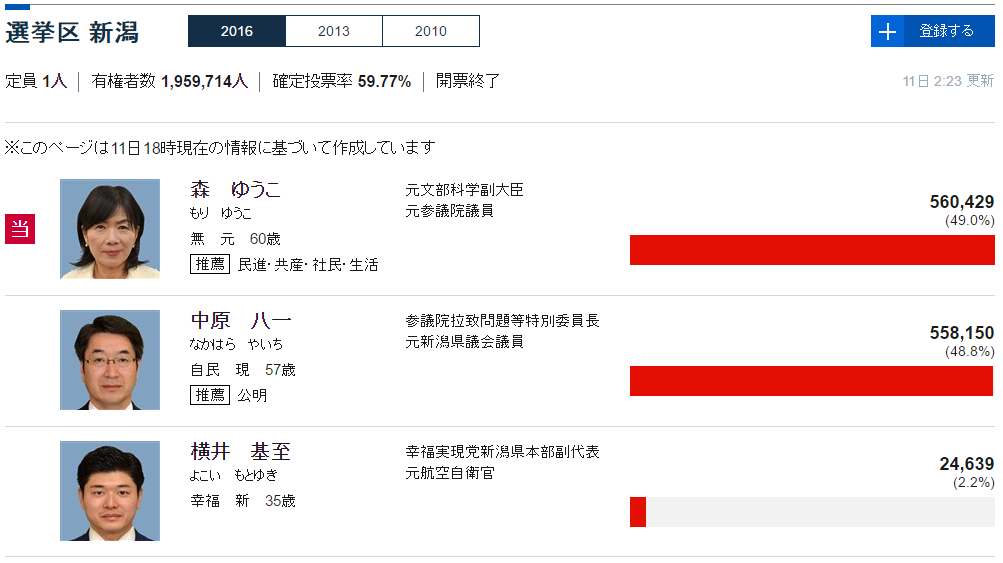
e.g. Niigata district at the 2016 Upper House Election in Japan
Close elections
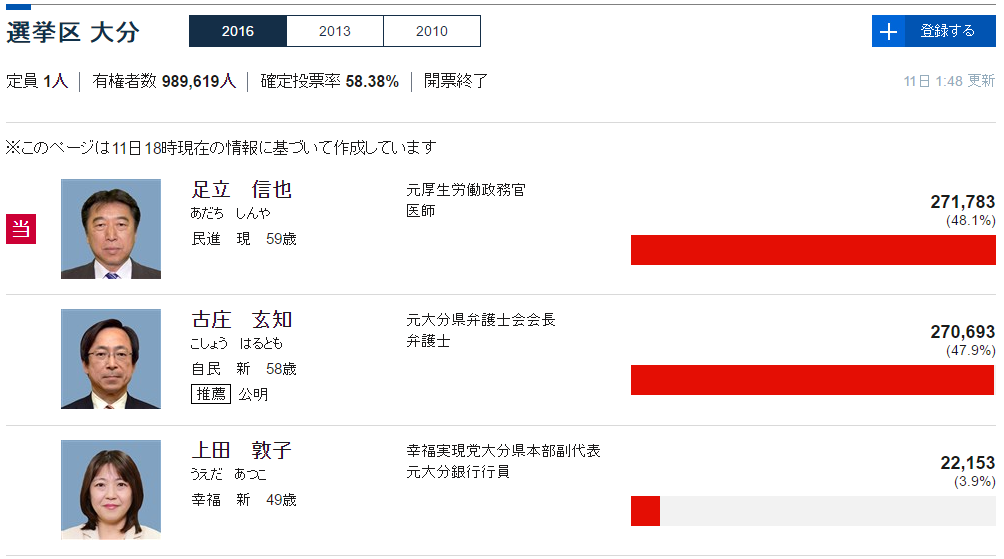
e.g. Oita district at the 2016 Upper House Election in Japan
Close elections

Which of the top two candidates won was plausibly random

Close elections
Regression Discontinuity Design
exploits these election
Today's Economics Lesson #2
Regression Discontinuity Design
e.g., Impact of admission to Osaka University
Exam score
Admitted
Not admitted
For these students
it's random
whether admitted or not
Today's Economics Lesson #2
Regression Discontinuity Design
e.g., Impact of representative vs direct democracy
population
Representative
Direct
For these municipalities
it's random
whether direct or not
(in Swedish municipalities in 1919)
1,500
Today's Economics Lesson #2
Regression Discontinuity Design
Then plot the outcome against exam score or population
Image Source: Figure 8 of Lee and Lemieux (2010)
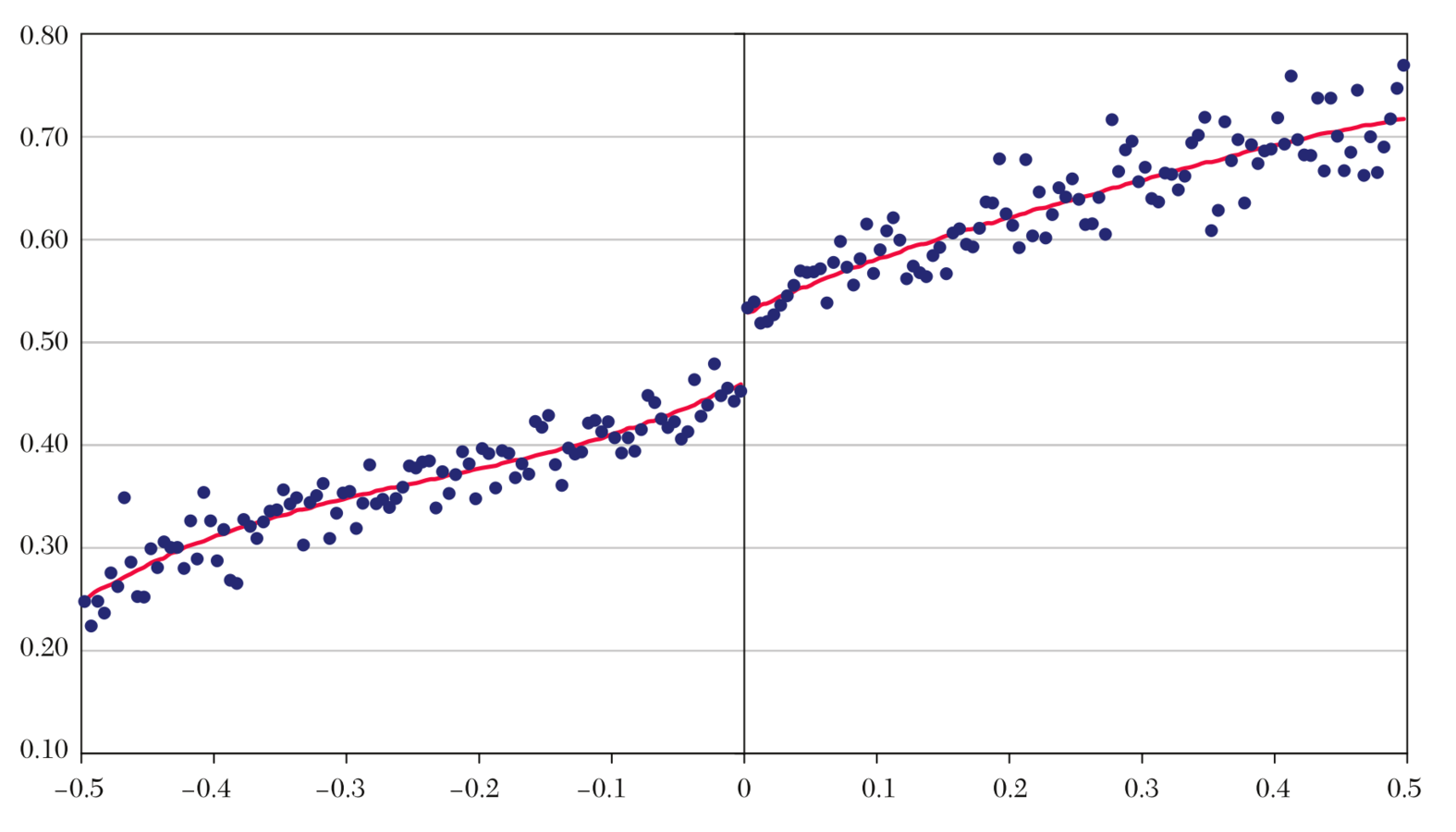
Bin average
Predicted value
Impact
Today's Economics Lesson #2
Regression Discontinuity Design
Then plot the outcome against exam score or population
Image Source: Figure 11 of Lee and Lemieux (2010)
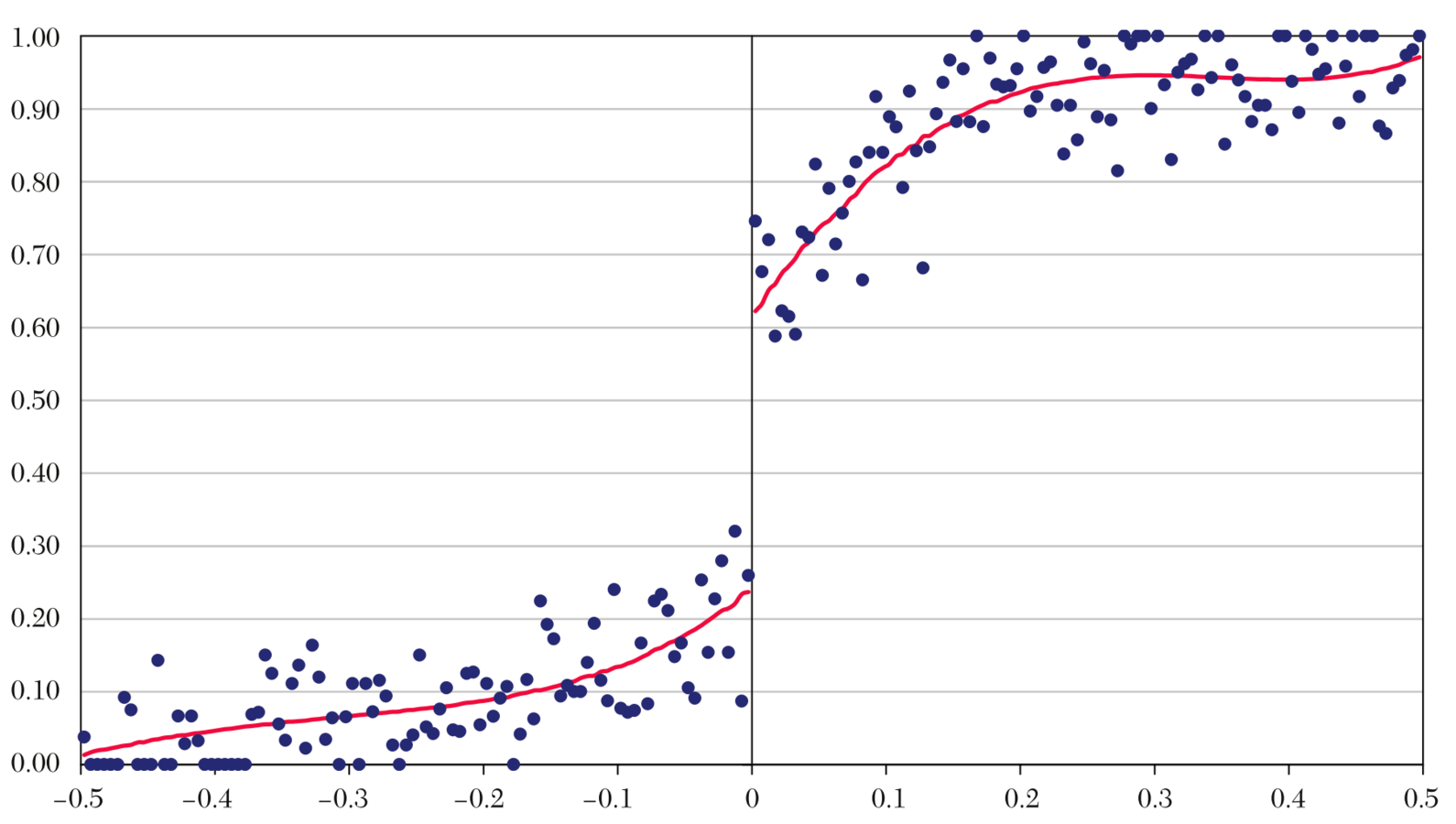
Impact
Today's Economics Lesson #2
Regression Discontinuity Design
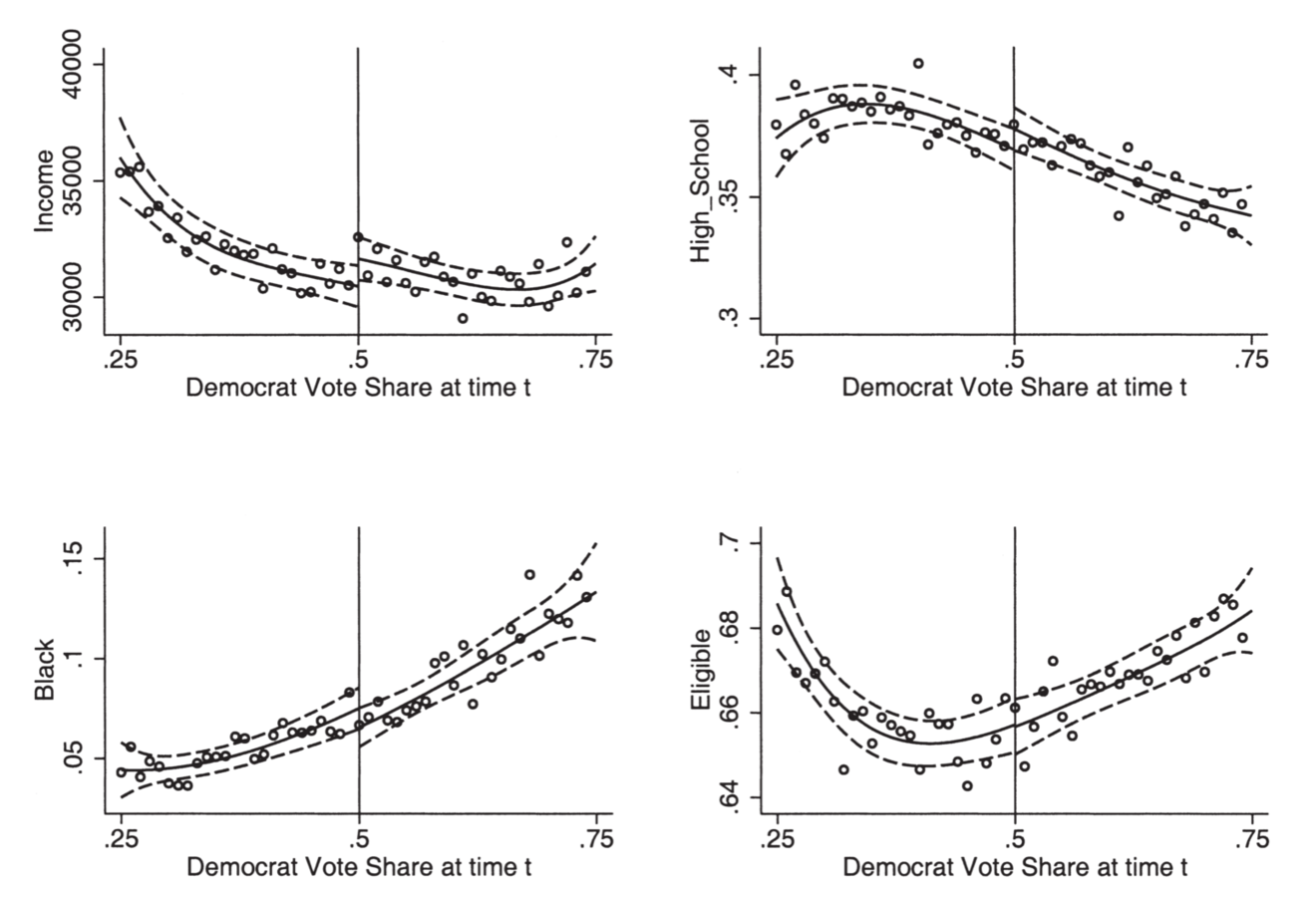
Also plot irrelevant characteristics to check randomness
Image Source: Figure 17 of Lee and Lemieux (2010)
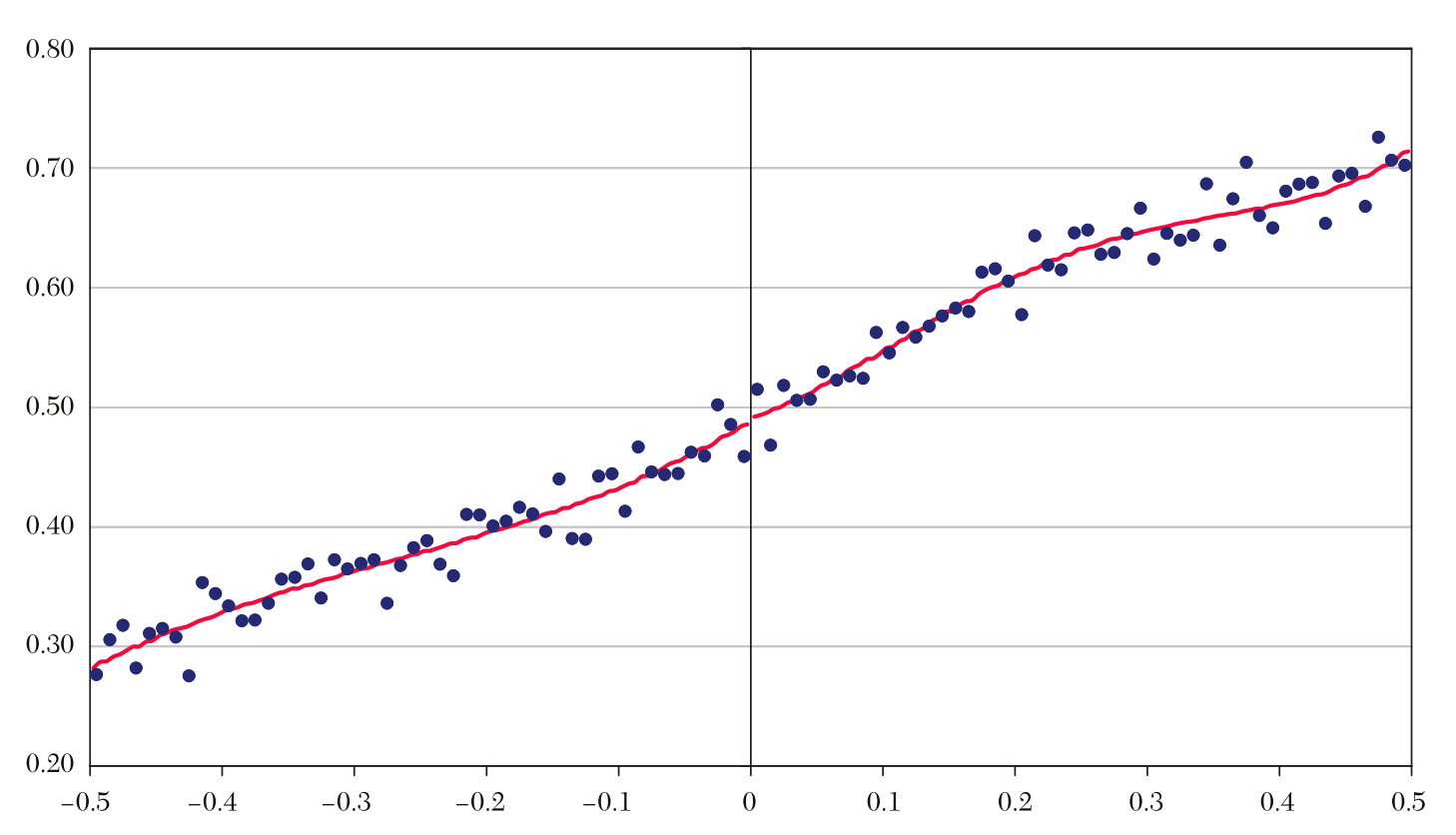
No difference
Today's Economics Lesson #2
Regression Discontinuity Design
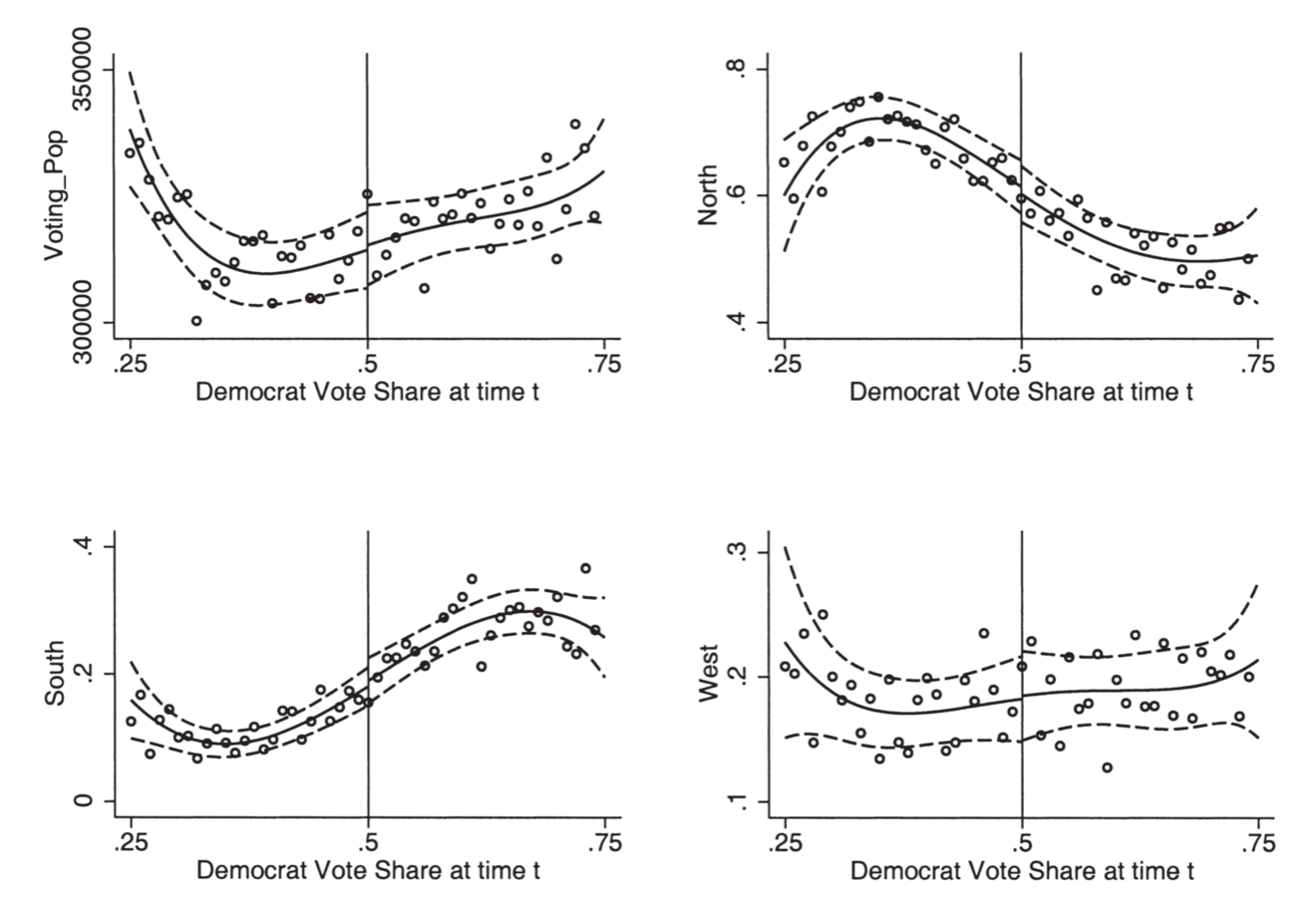
Image Source: Figure 16 of Lee and Lemieux (2010)
Insignificant
difference
Also plot irrelevant characteristics to check randomness
Take this idea to US Lower House Elections, 1946-1994
Plot outcomes against Democratic Party's candidate vote share
Vote share (%)
100
50
0
If who wins is random in close elections, districts around 50% vote share should be similar
Testing the no-commitment assumption
Districts around 50% vote share are indeed similar
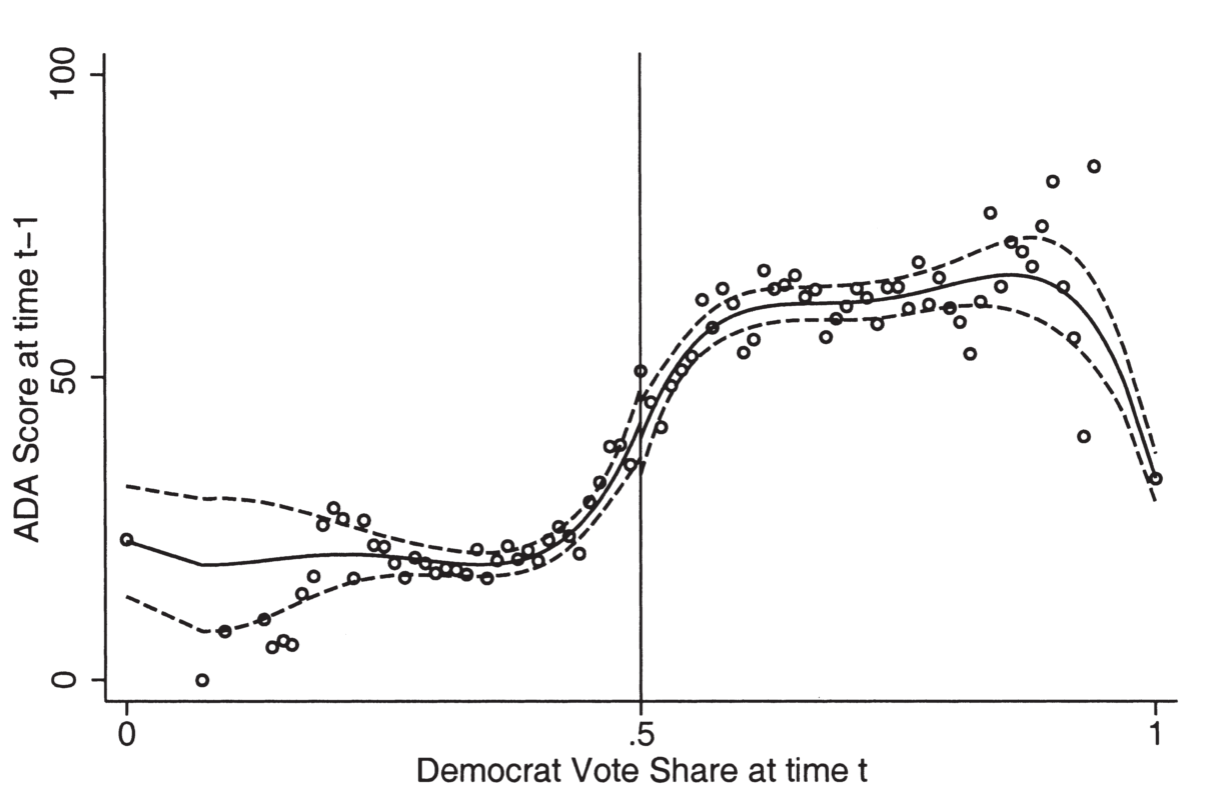
Source: Figure 3 of Lee et al. (2004)
Districts around 50% vote share are indeed similar
Source: Figure 4 of Lee et al. (2004)
Outcome to look at:
Roll call votes
0
100
Liberal
Conservative

Quantify how liberal voting behaviour is (known as ADA Score)
Testing the no-commitment assumption (cont.)
Districts around 50% vote share are indeed similar
Source: Figure 5 of Lee et al. (2004)
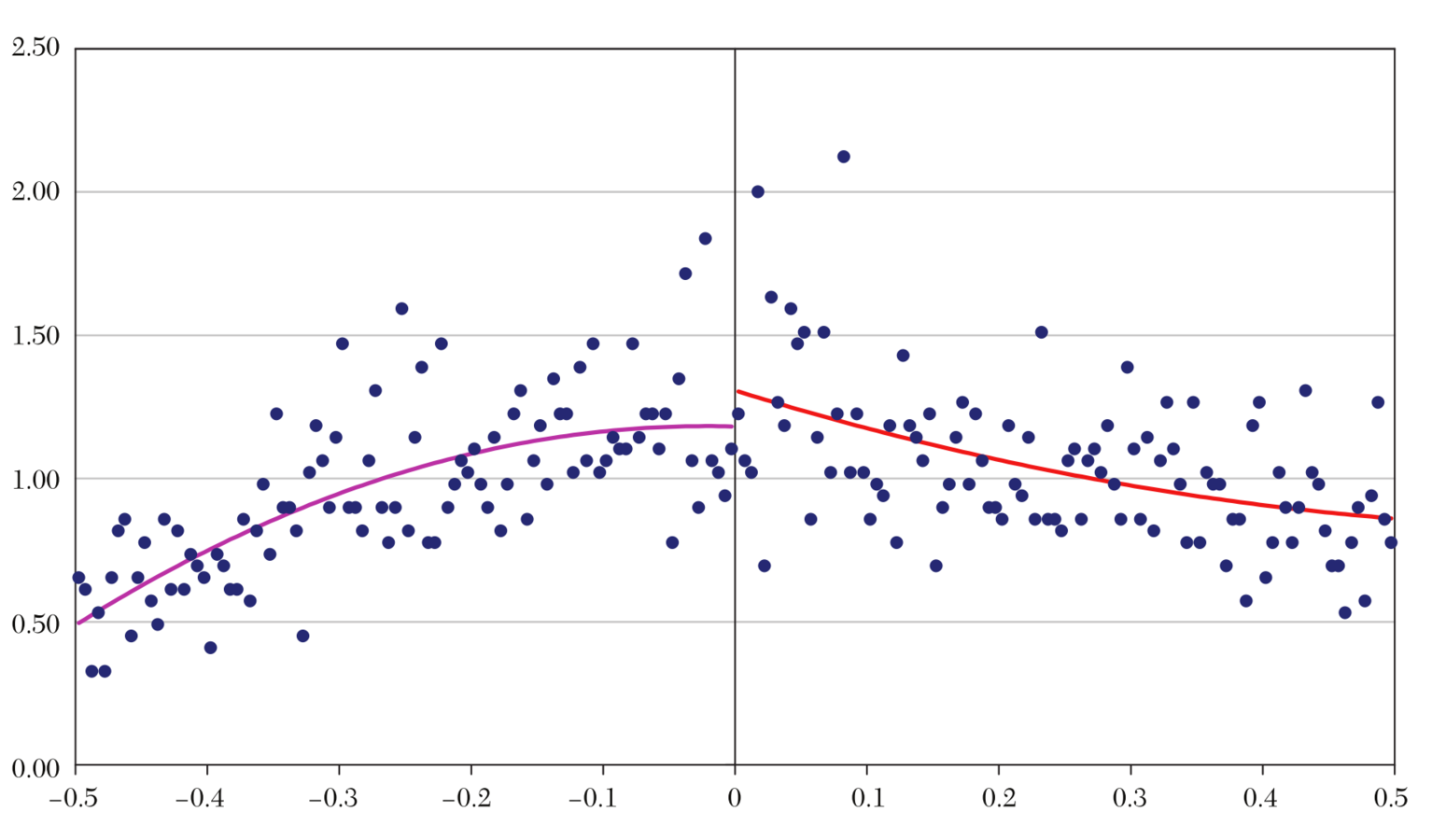
But the winner's voting behaviour in Congress differs a lot
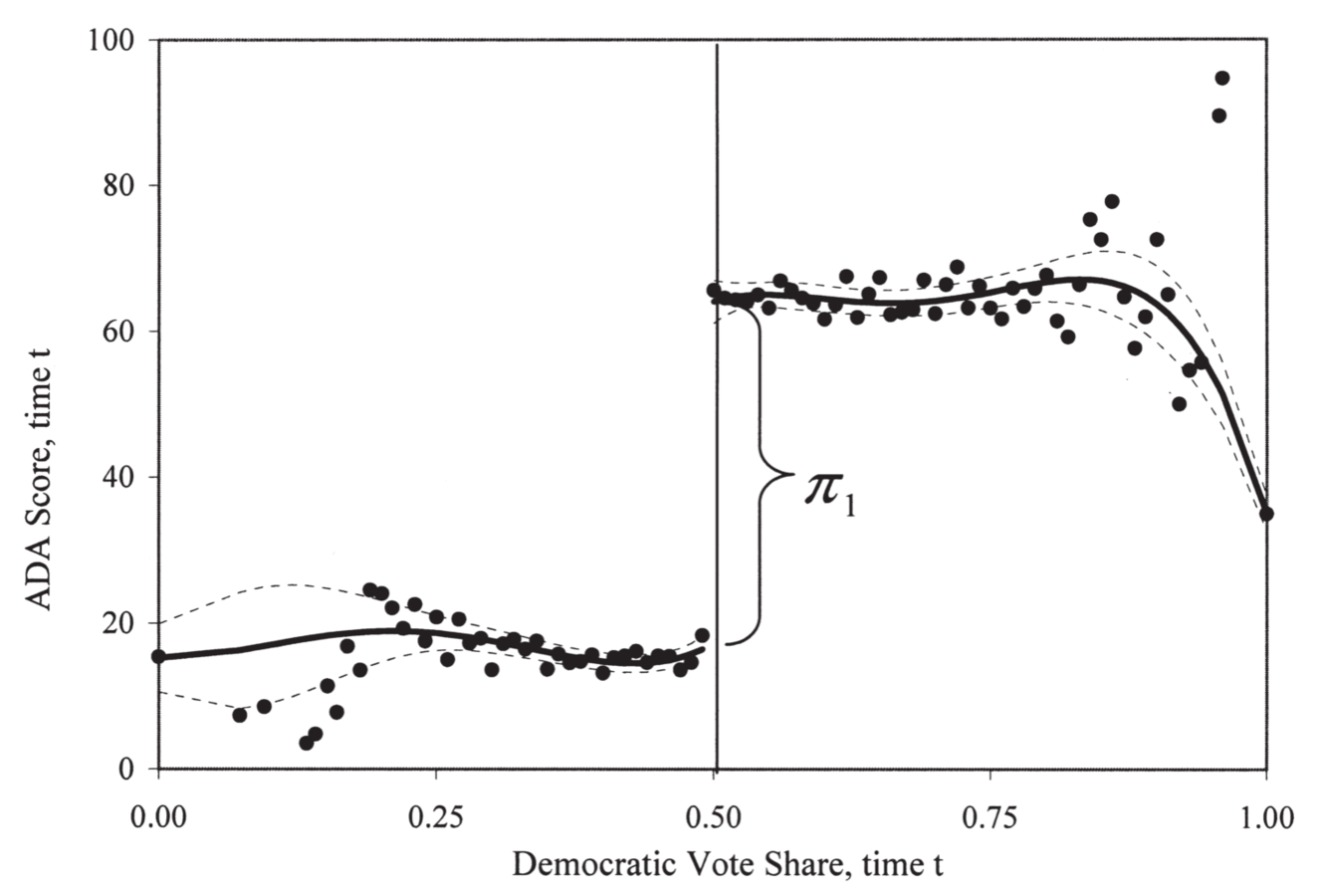
Source: Figure 2A of Lee et al. (2004)
Policy
Divergence
Summary
Available evidence suggests
politicians choose their ideal policy, not the median voter's
Citizen-candidate model helps understand such a world of politics
One candidate runs unopposed
Two party system (and its perpetual tendency)
Next lecture
Who becomes a politician?

Next lecture
Why do politicians form
political parties?
Image source: nihonseiji.com/parties
This lecture is based on the following academic articles and books:
Besley, Timothy, and Stephen Coate. 1997. “An Economic Model of Representative Democracy.” Quarterly Journal of Economics 112(1): 85–114.
See also chapter 5 of Persson and Tabellini. 2000. Political Economics (MIT Press).
Lee, D. S., E. Moretti, and M. J. Butler. 2004. “Do Voters Affect or Elect Policies? Evidence from the U. S. House.” Quarterly Journal of Economics 119(3): 807–59.
Politics through the Lens of Economics: Lecture 4 Citizen-candidate Model
By Masayuki Kudamatsu
Politics through the Lens of Economics: Lecture 4 Citizen-candidate Model
- 4,380



