The SpectralDNS project:

Shenfun - automating the spectral Galerkin method

Mikael Mortensen, Miroslav Kuchta

Department of Mathematics, University of Oslo

and

Lisandro Dalcin

King Abdullah University of Science and Technology

International Conference on Computational Science and Engineering, Simula 23/10 - 2017

Background to

the spectralDNS/shenfun project

Started out as a toy project for

myself and Hans Petter

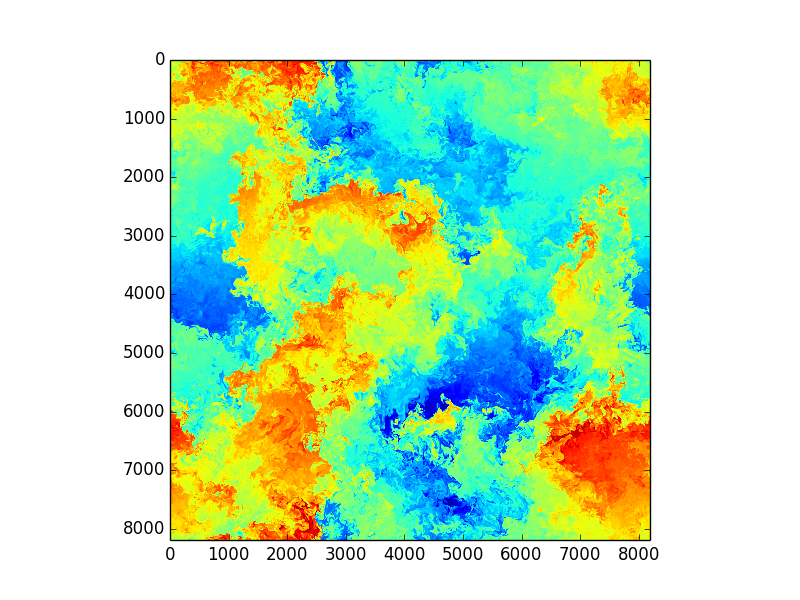
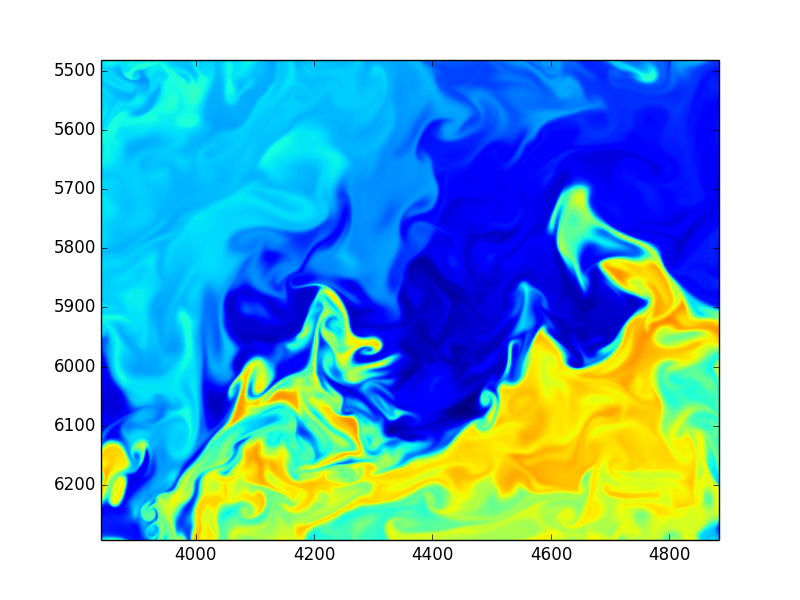
Using Fourier transformed Navier Stokes equations

We knew Direct Numerical Simulations (DNS) of turbulence were performed with low-level Fortran or C

8192^3 \text{ mesh}

Would it be possible to write a competitive, state of the art turbulence solver in Python?

From scratch?

(Not just wrapping a Fortran solver)

Using only standard Python modules numpy/scipy/mpi4py?

Can we make this solver run on thousands of cores ?

With billions of unknowns?

As fast as C/fortran?

Long story short - Yes 

  1. Vectorize everything (Numpy)
  2. Using FFTW we implement parallel (MPI) Fast Fourier Transforms (FFT)
  3. 100 lines of pure Python / Numpy  ~30% slower than optimized C++ code
  4. Using Cython, we were par with C++

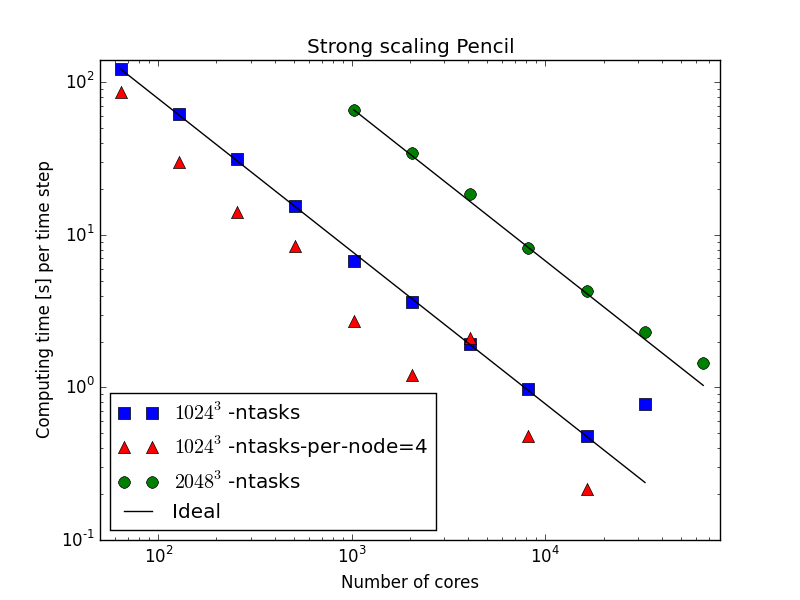
65,536 cores!

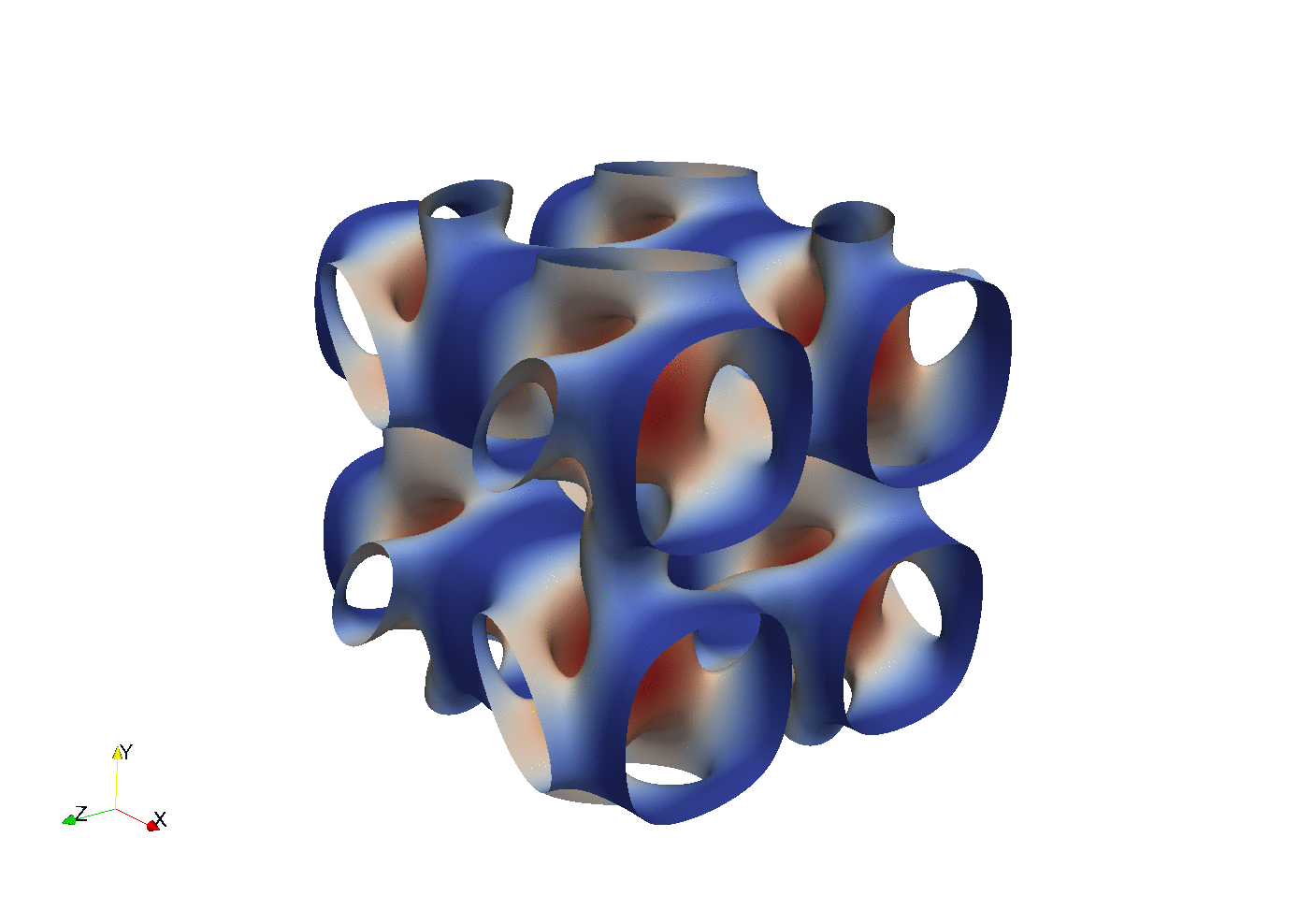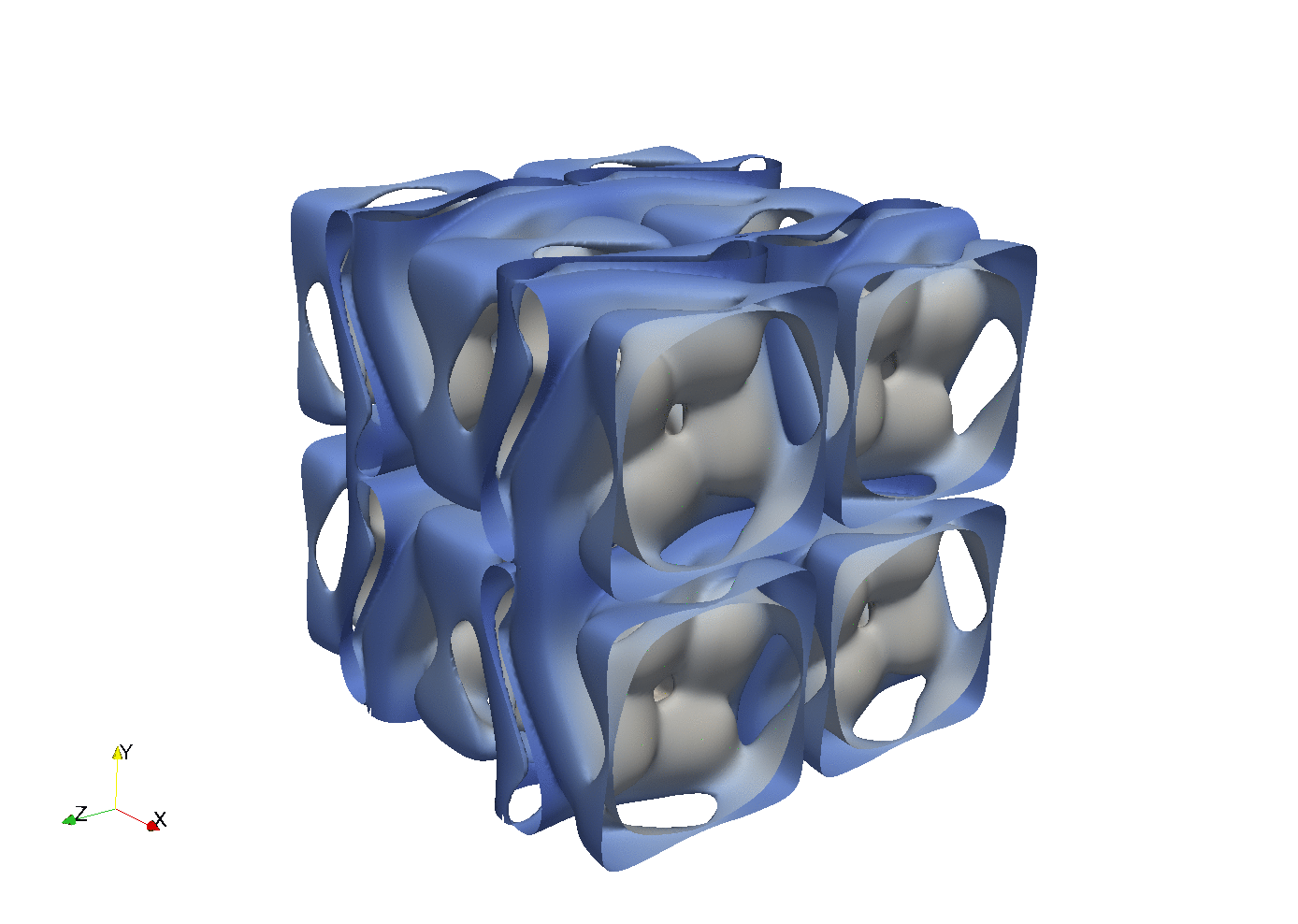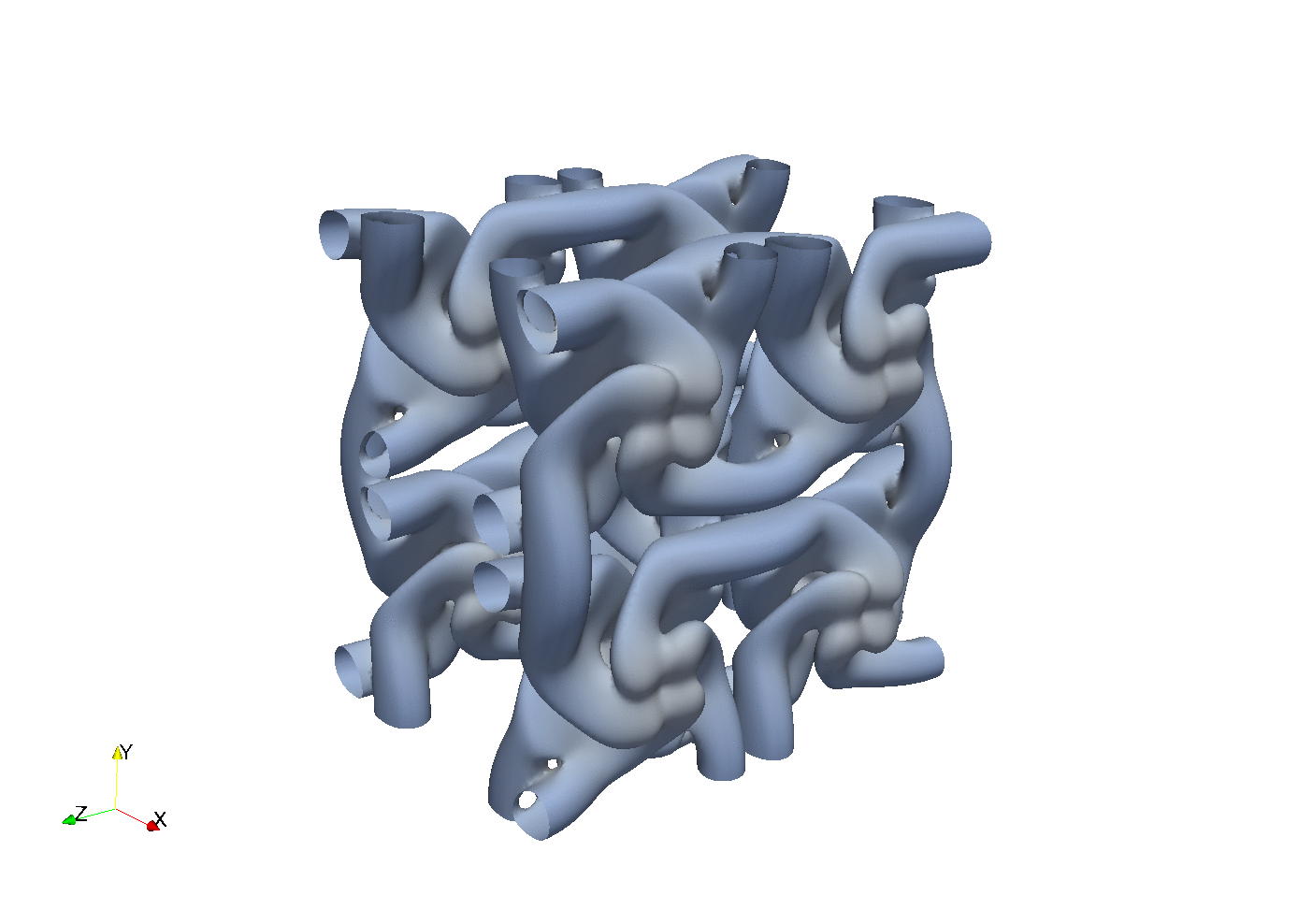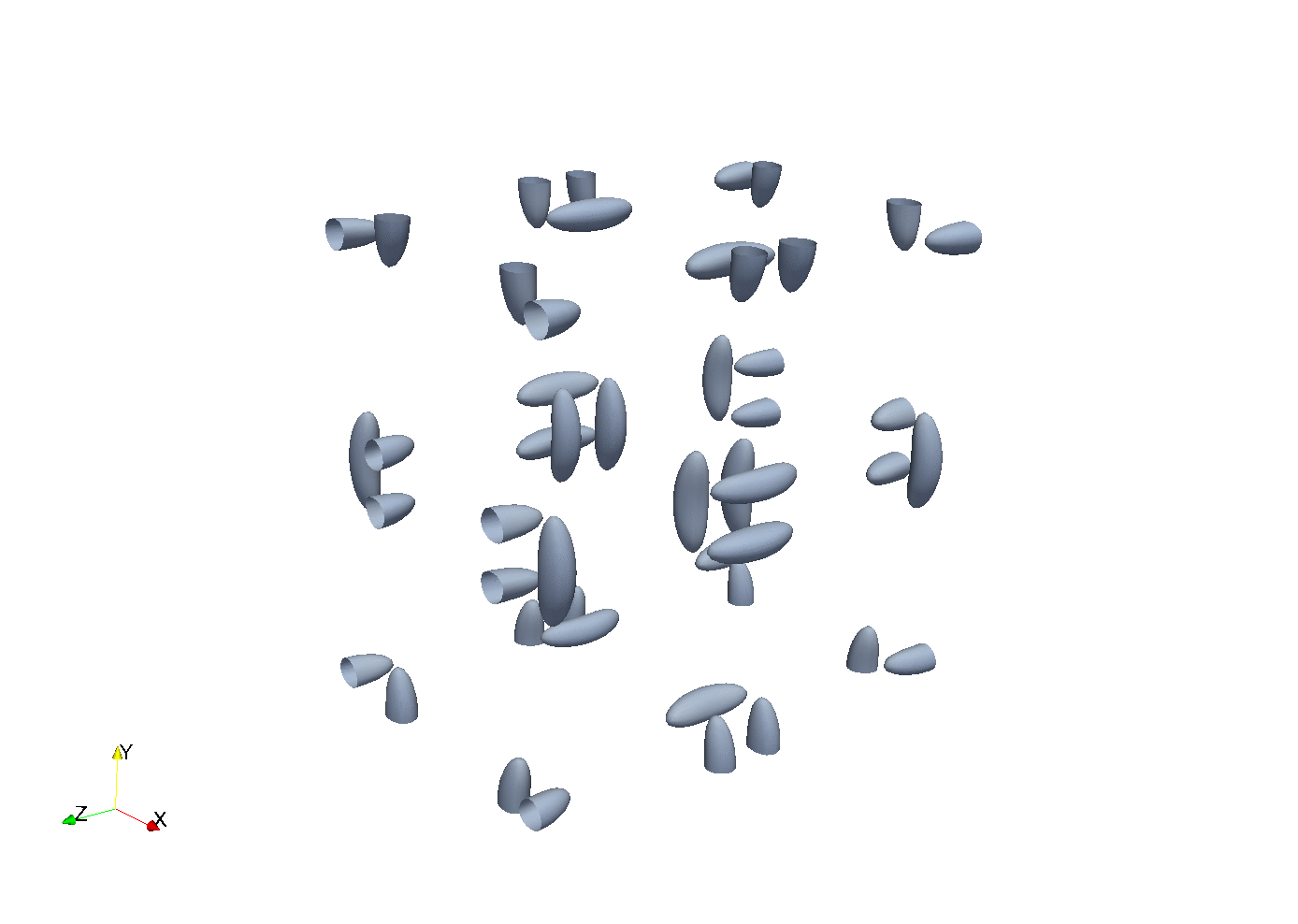
Gist

Concept proven

and Hans Petter is off to write 4 new books,

but with new collaborators, and fast transforms in place we can do so much more

mpi4py-fft

https://bitbucket.org/mpi4py/mpi4py-fft

With Lisandro Dalcin at KAUST

~ 500 lines of  Python code

With the newly released

we can do any transform from FFTW in parallel

Highly configurable and fast

We can now implement

the spectral Galerkin method

on non-periodic domains, with different types

of boundary conditions (Dirichlet/Neumann)

Not just periodic Fourier

The spectral Galerkin method employs global basis functions with the Galerkin approximation

  1. Choose global basis (test) functions satisfying the correct boundary conditions. Usually modified Chebyshev or Legendre polynomials, or Fourier exponentials

  2. Transform PDEs to weak variational forms using the method of weighted residuals

  3. Assemble and solve system of equations

u(x) = \displaystyle\sum_{k=0}^{N-1} \hat{u}_k \phi_k(x)

Solution

Expansion coefficients

(unknowns)

Global basis functions

and it works in three steps:

Spectral Galerkin

Poisson example

\nabla^2 u(x) = f(x) \quad \text{for} \quad x \in [-1, 1]
u(\pm 1) = 0

1) Create a basis that satisfies boundary conditions, e.g.,

\phi_k(x) = L_k(x) - L_{k+2}(x) \quad V = \text{span}\{\phi_k\}_{k=0}^{N-3}
\displaystyle \int_{-1}^{1}v \nabla^2 u \, w dx = \int_{-1}^{1} vf w dx
\text{where } w(x) \text{ is a weight function and } u \in V \text{ is trial function}

(Legendre polynomial order k+2)

2) Transform PDE to variational form using test function  

v \in V

3) Assemble and solve linear system of equations

\text{Find } u \in V, \text{such that}
\left(v, \nabla^2 u \right)_w^N = \left(v, f \right)_w^N \quad \forall v \in V
A_{kl} \hat{u}_l = \tilde{f}_k
\hat{u}_k = A_{kl}^{-1} \tilde{f}_l
\text{Leading to a linear algebra problem:}
\left( v, u\right)_w^N \approx \displaystyle \int_{-1}^{1} vu w dx
u(x) = \displaystyle\sum_{l=0}^{N-1} \hat{u}_l \phi_l(x)
v = \phi_k

Trial function

Test function

With quadrature notation

3 steps - Sounds generic and easy?

Let's automate!

from fenics import *

mesh = UnitSquareMesh(8, 8)
V = FunctionSpace(mesh, 'CG', 1)

# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
f = Constant(-6.0)
a = inner(grad(u), grad(v))*dx
L = f*v*dx
  • Automates the finite element method (Galerkin)
  • Basis functions with local support

  • Finite accuracy (not spectral)

How?

Shenfun

https://github.com/spectralDNS/shenfun

Python package (~3k loc) for automating the spectral Galerkin

method for high performance computing on tensor product grids

  • A FEniCS like interface with a simple form language
  • MPI - invisible to the user: mpi4py-fft (with Lisandro Dalcin)
  • Fourier - Chebyshev - Legendre modified basis functions
  • Extremely fast (!), order optimal, direct solvers for Poisson, Helmholtz and Biharmonic problems (with Miroslav Kuchta)

Shenfun implementation of 1D Poisson problem

import numpy as np
from shenfun import TestFunction, TrialFunction, inner, div, grad, chebyshev

N = 20
V = chebyshev.ShenDirichletBasis(N, plan=True)
v = TestFunction(V)
u = TrialFunction(V)

# Assemble stiffness matrix
A = inner(v, div(grad(u)))

# Some consistent right hand side
f = Function(V, False)
f[:] = -2

# Assemble right hand side
f_hat = inner(v, f)

# Solve equations and transform spectral solution to real space
f_hat = A.solve(f_hat)
fj = V.backward(f_hat)

x = V.mesh(N)
assert np.allclose(fj, 1-x**2)

Very similar to FEniCS!

just with spectral accuracy

(1) Create basis

(2) Variational forms

(3) Solve system

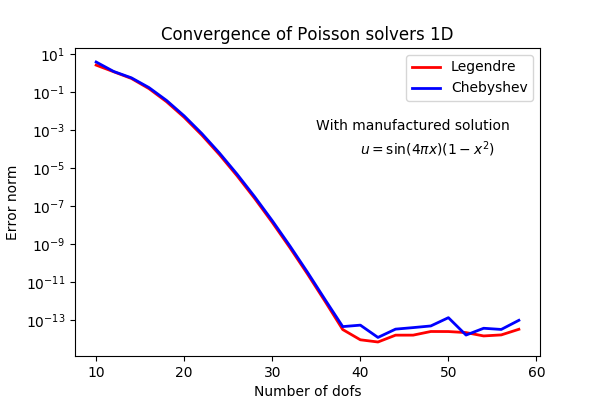
2D/3D/4D..  Tensor product spaces

Cartesian products of Fourier and Chebyshev/Legendre bases

u(x,y,z,t) = \displaystyle \sum_{k}\sum_{l}\sum_{m} \hat{u}_{klm}(t) \phi_k(x)\phi_l(y)\phi_m(z)
W(x,y,z) = V(x) \times V(y) \times V(z)

Any Cartesian combination of spaces (ultimately)

With solutions of the form:

Unknown expansion coefficients

Tensor product spaces

Implementation

from shenfun import *
from mpi4py import MPI

comm = MPI.COMM_WORLD
N = (20, 30)

# Create two bases
V0 = chebyshev.ShenDirichletBasis(N[0])
V1 = fourier.R2CBasis(N[1])

# Create tensor product space
T = TensorProductSpace(comm, (V0, V1))
v = TestFunction(T)
u = TrialFunction(T)

A = inner(v, div(grad(u)))

# Or 3D
V2 = fourier.C2CBasis(40)
T3 = TensorProductSpace(comm, (V0, V2, V1))
v = TestFunction(T3)
u = TrialFunction(T3)

A = inner(v, div(grad(u)))

MPI under the hood

using mpi4py-fft

on tensor product grids like:

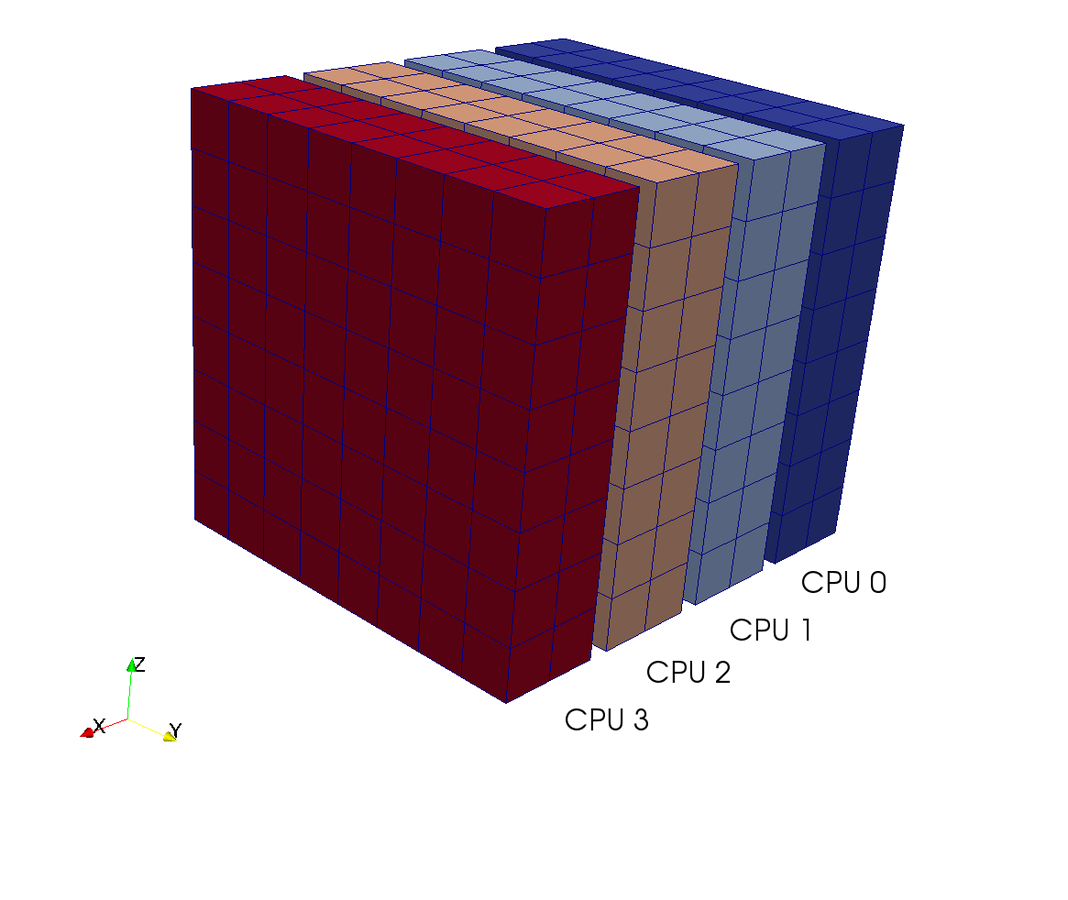
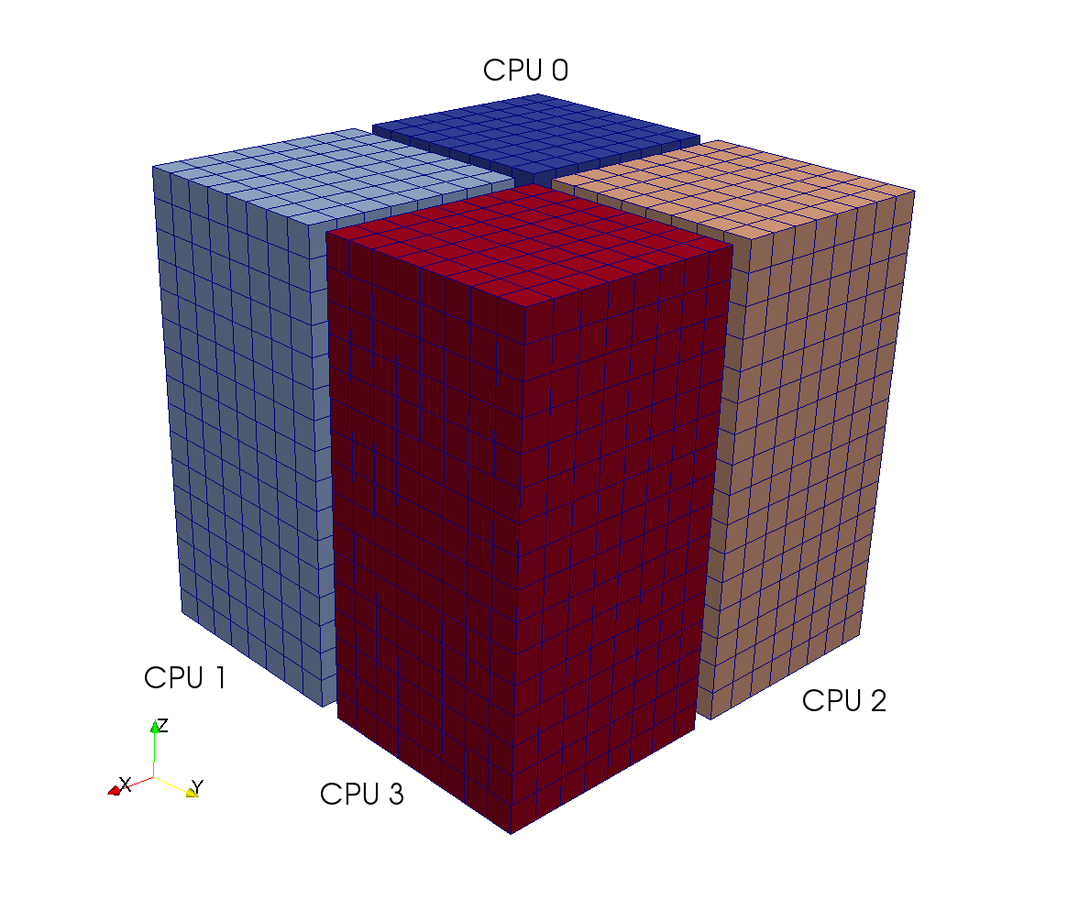
Slab

Pencil

A simple form language

influenced heavily by UFL/FEniCS

Mathematical operators act on test, trial, or functions with data 

V = TensorProductSpace(comm, (V0, V1, V2))

# Form arguments:
v = TestFunction(V)
u = TrialFunction(V)
u_ = Function(V, False)

# Forms
du = grad(u_)
d2u = div(du) 
cu = curl(du)
dudx = Dx(u_, 0)

Inner products and projections

A = inner(v, u)    # Bilinear form, assembles to matrices
f = inner(v, u_)   # Linear form, assembles to vector
project(div(grad(u_)), V)  # projection to V

Fast transforms

u_hat = V.forward(u, u_hat)        u = V.backward(u_hat, u)

Move back and forth between         and        using fast transforms

Periodic basis using fast Fourier transforms

Non-periodic basis using fast Chebyshev transforms (not for Legendre)

\blue{u}
\blue{\hat{u}}
\blue{u}(x,y,z) = \displaystyle\sum_{k=0}^{N-1} \sum_{l=0}^{N-1} \sum_{m=0}^{N-1} \blue{\hat{u}_{klm}} \phi_k(x)\phi_l(y)\phi_m(z)

Nonlinearities

all treated with pseudo-spectral techniques

u \times \nabla \times u
u \cdot u
u | u |^2

(1) Compute inverse 

u = T.backward(u_hat)

with dealiasing using

3/2-rule (padding) or 2/3-rule

(3) Transform back to spectral space 

w = u*u

(2) Compute nonlinearity 

w_hat = T.forward(w)
T = TensorProductSpace(comm, (V0, V1, V2))

Fast direct solvers

1D: \text{Find } u \in V, \text{such that}
\left(v, \nabla^2 u \right)_w^N = \left(v, f \right)_w^N \quad \forall v \in V
A_{kl} \hat{u}_l = \tilde{f}_k
\text{Leading to a linear algebra problem:}

Fourier: A is diagonal

Modified Legendre: A is diagonal

Modified Chebyshev: A sparse  - solved as tridiagonal matrix

Fast direct solvers

2 non-periodic directions

\left(v, \nabla^2 u \right)_w^N = \left(v, f \right)_w^N \quad \forall v \in V\times V
\text{Find } u \in V\times V, \text{such that}
A_{km} B_{nl}\hat{u}_{mn} + B_{km} A_{nl} \hat{u}_{mn} = \tilde{f}_{kl}

Matrix form:

A \hat{u} B + B \hat{u} A^T = \tilde{f}

Sparse matrices A (stiffness) and B (mass) are 1D matrices of basis

Very fast direct solvers implemented in parallel using matrix decomposition method

Linear algebra:

Complex Ginzburg-Landau

example

\frac{\partial u}{\partial t} = \nabla^2 u + u -(1+1.5i)u |u|^2


2D periodic (x, y) \( \in [-50, 50]^2 \)

Use Fourier in both directions

Weak form, only spatial discretization:

\frac{\partial (v, u)^N}{\partial t} = -(\nabla v, \nabla u)^N + (v, u -(1+1.5i)u |u|^2)^N
(2\pi)^2\frac{\partial \hat{u}}{\partial t} = -(\nabla v, \nabla u)^N + (v, u -(1+1.5i)u |u|^2)^N

Complex Ginzburg-Landau

example

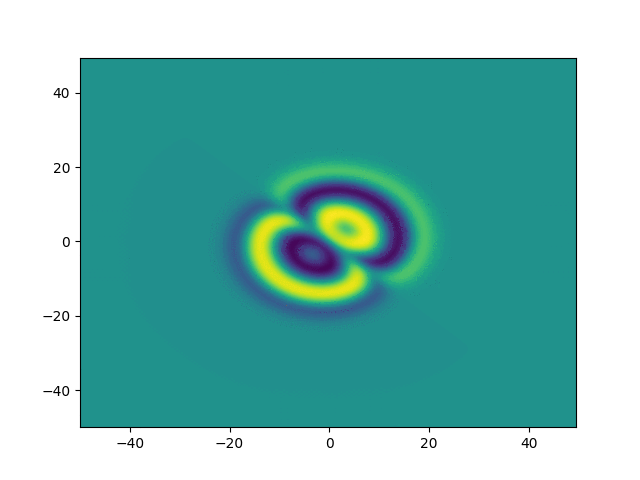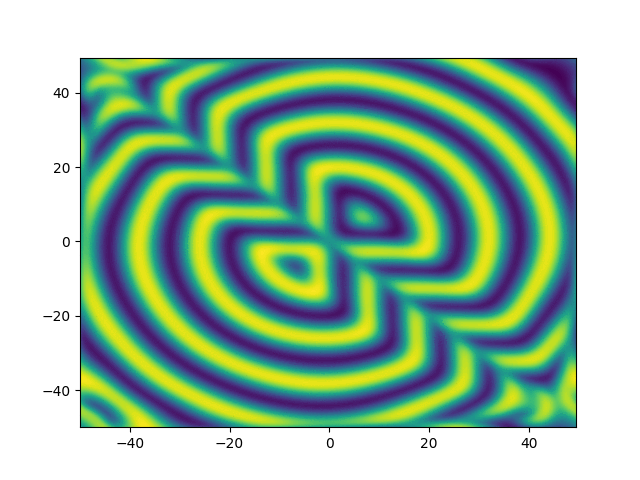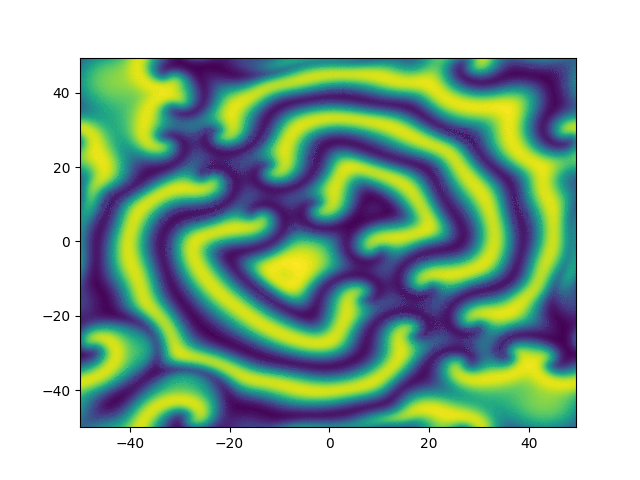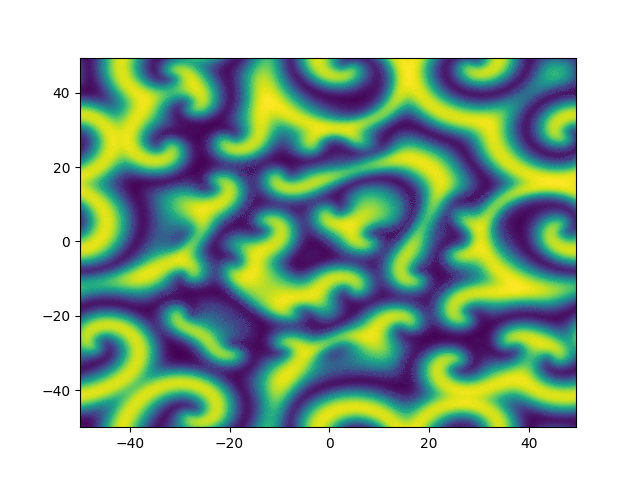
2D periodic (x, y) \( \in [-50, 50]^2 \)

import sympy
from shenfun.fourier.bases import R2CBasis, C2CBasis
from shenfun import inner, grad, TestFunction, TrialFunction, \
    Function, TensorProductSpace

# Use sympy to set up initial condition
x, y = sympy.symbols("x,y")
ue = (x + y)*sympy.exp(-0.03*(x**2+y**2))

N = (200, 200)
K0 = C2CBasis(N[0], domain=(-50., 50.))
K1 = C2CBasis(N[1], domain=(-50., 50.))
T = TensorProductSpace(comm, (K0, K1))
u = TrialFunction(T)
v = TestFunction(T)
U = Function(T, False)

def compute_rhs(rhs, u_hat, U, T):
    rhs = inner(grad(v), -grad(U), output_array=rhs, uh_hat=u_hat)
    rhs /= (2*np.pi)**2
    rhs += u_hat
    rhs -= T.forward((1+1.5j)*U*abs(U)**2, w0)
    return rhs

# And, e.g., Runge-Kutta integrator
#
#

Key code:

(2\pi)^2\frac{\partial \hat{u}}{\partial t} = -(\nabla v, \nabla u)^N + (v, u -(1+1.5i)u |u|^2)^N

Navier Stokes 

Turbulent channel flow

3D tensor product space

2 Fourier bases +

Modified Chebyshev bases for wall normal direction

Kim and Moin modified version of Navier-Stokes:

\mathcal{H}

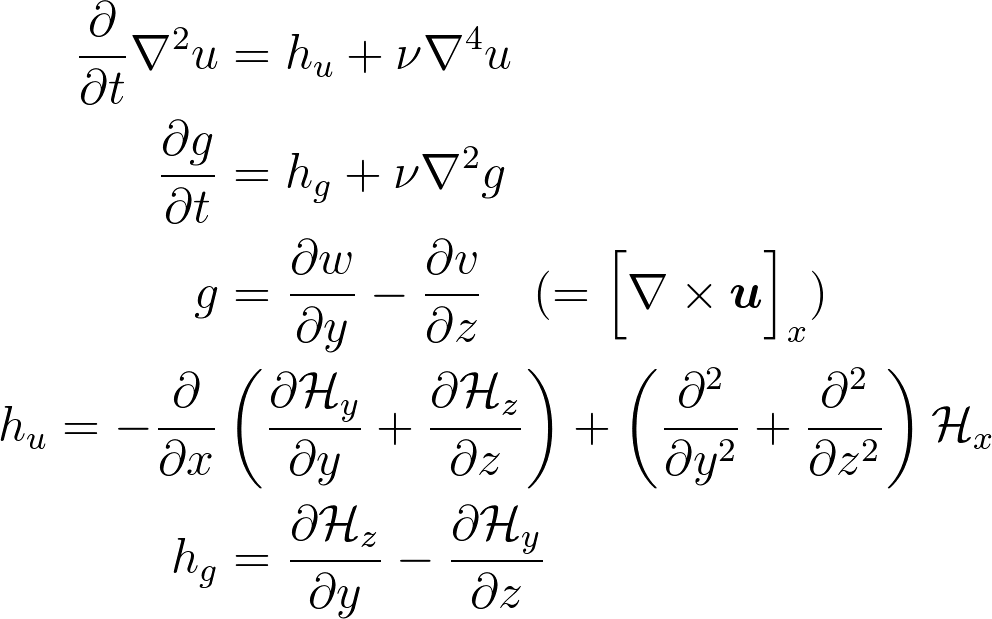
is convection

Wall normal velocity

Wall normal vorticity

Navier Stokes 

Turbulent channel flow

512\times 1024\times 1024

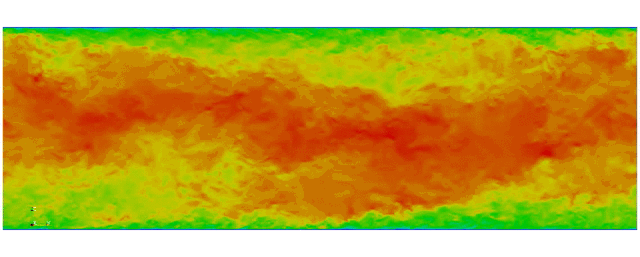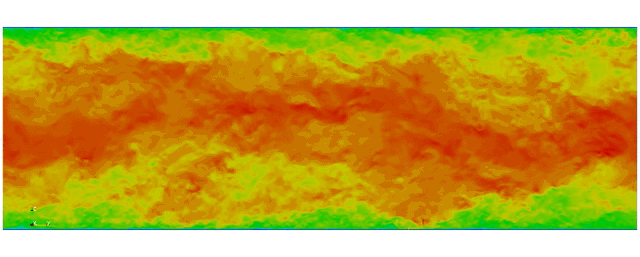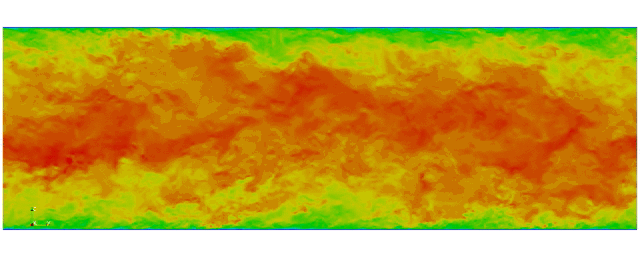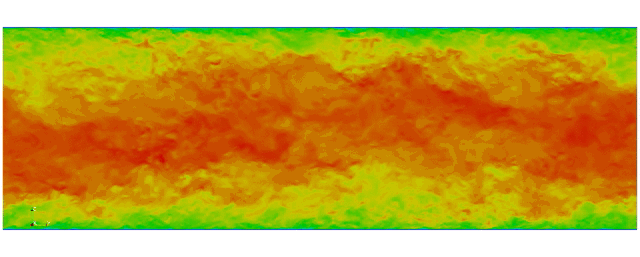
First fully spectral DNS with 

3D Tensor product mesh:

Shaheen II at KAUST

\text{Re}_{\tau} > 2000

Some more demos prepared with Hans Petter's doconce:

Thank you for your time! 

http://github.com/spectralDNS/shenfun

Questions?

Presented at the International Conference on Computational Science and Engineering 23/10-2017

By Mikael Mortensen

Made with Slides.com

Presented at the International Conference on Computational Science and Engineering 23/10-2017

  • 2,087

More from Mikael Mortensen