1.5 McCulloch Pitts Neuron
Your first model

Recap: Six jars
What we saw in the previous chapter?
(c) One Fourth Labs

Learning
Loss
Model
Data

Task
Evaluation
Artificial Neuron
What is the fundamental building block of Deep Learning ?
(c) One Fourth Labs

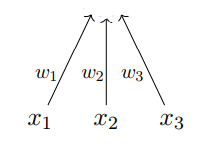

f
Recall Biological Neuron
Where does the inspiration come from ?
(c) One Fourth Labs

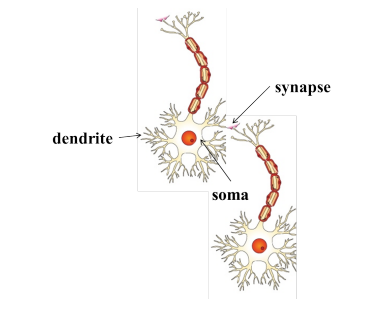
The Model
When and who proposed this model ?
(c) One Fourth Labs

The early model of an artificial neuron is introduced by Warren McCulloch and Walter Pitts in 1943. The McCulloch-Pitts neural model is also known as linear threshold gate.
Walter Pitts was a logician who proposed the first mathematical model of a neural network. The unit of this model, a simple formalized neuron, is still the standard of reference in the field of neural networks. It is often called a McCulloch–Pitts neuron.
Warren McCulloch was a neuroscientist who created computational models based on threshold logic which split the inquiry into two distinct approaches, focused on biological processes in the brain and application of neural networks to artificial intelligence.


* Images adapted from https://www.i-programmer.info/babbages-bag/325-mcculloch-pitts-neural-networks.html
The Model
How are we going to approach this ?
(c) One Fourth Labs

Learning
Loss
Model
Data


Task




Evaluation
The Model
What is the mathematical model ?
(c) One Fourth Labs

One parameter, b


f
g
McCulloch and Pitts proposed a highly simplified computational model of the neuron.
The inputs can be excitatory or inhibitory
g aggregates the inputs and the function f takes a decision based on this aggregation.
if any
is inhibitory, else
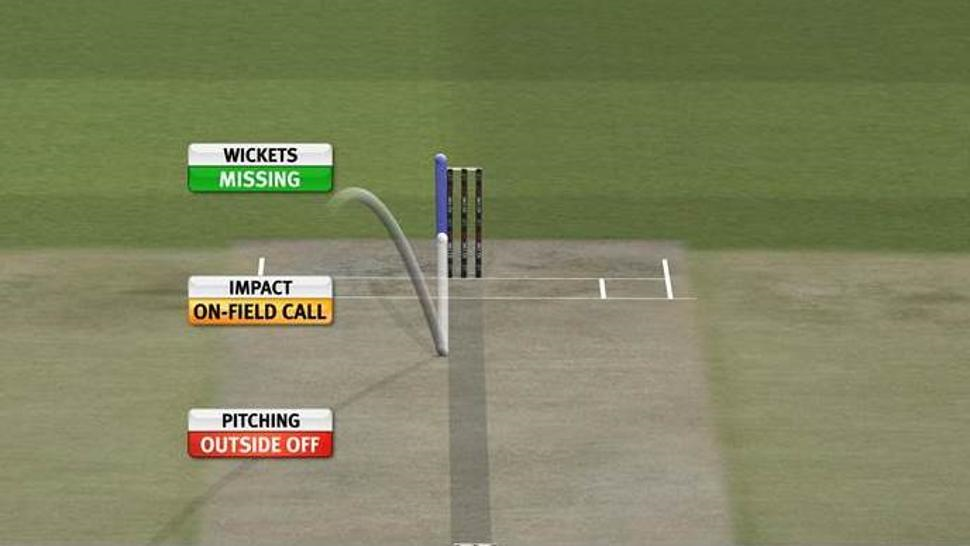
Data and Task
What kind of data and tasks can MP neuron process ?
| Pitch in line |
|---|
| 1 |
| 0 |
| 1 |
| 0 |

\(x_1\)
(pitch)
\(x_3\)
(stumps off)
\(x_2\)
(impact)
\(y\) (LBW)
(c) One Fourth Labs

| Pitch in line |
Impact | Missing stumps | Is it LBW? (y) |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| Pitch in line |
Impact | Missing stumps |
|---|---|---|
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| Pitch in line |
Impact |
|---|---|
| 1 | 0 |
| 0 | 1 |
| 1 | 1 |
| 0 | 1 |
Data and Task
What kind of data and tasks can MP neuron process ?
| Pitch in line |
|---|
| 1 |
| 0 |
| 1 |
| 0 |
\(x_1\)
(pitch)
\(x_3\)
(stumps off)
\(x_2\)
(impact)
\(y\) (LBW)
(c) One Fourth Labs

| Pitch in line |
Impact | Missing stumps | Is it LBW? (y) |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| Pitch in line |
Impact | Missing stumps |
|---|---|---|
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| Pitch in line |
Impact |
|---|---|
| 1 | 0 |
| 0 | 1 |
| 1 | 1 |
| 0 | 1 |
Data and Task
What kind of data and tasks can MP neuron process ?
(c) One Fourth Labs

Boolean inputs
Boolean output
\(x_1\)
b
| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| Like (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |







| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
?
| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
\(x_2\)
\(x_n\)
\(y\)
Loss Function
How do we compute the loss ?
(c) One Fourth Labs

| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| Like (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |









| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| Like (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| Prediction | 0 |
Loss Function
How do we compute the loss ?
(c) One Fourth Labs

| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| Like (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |


















| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| Like (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| Prediction | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
Loss Function
How do we compute the loss ?
(c) One Fourth Labs

| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| Like? (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| prediction | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| loss | 0 | 0 | 1 | -1 | 0 | 0 | -1 | 1 | 0 | 0 |










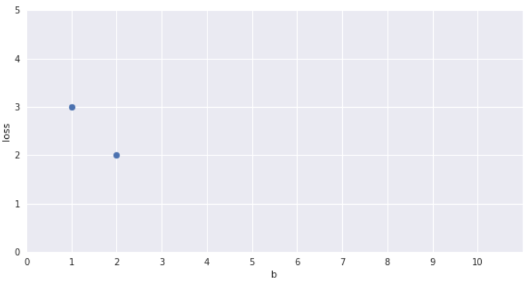
Learning Algorithm
How do we train our model?
(c) One Fourth Labs

Only one parameter, can afford Brute Force search

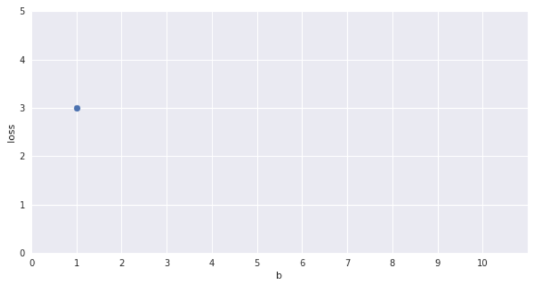
| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| Like? (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| prediction | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
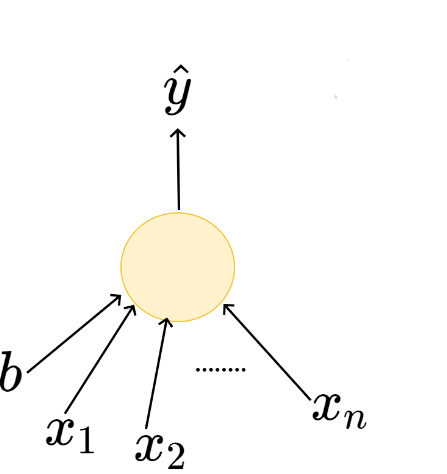
| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| Like? (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| prediction | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
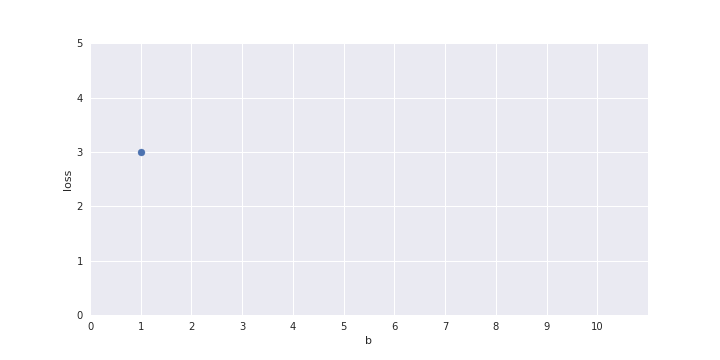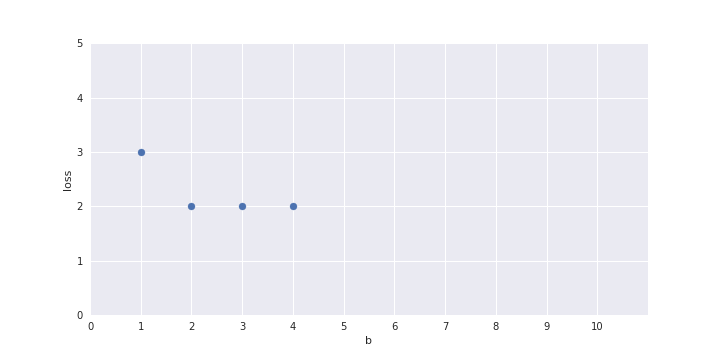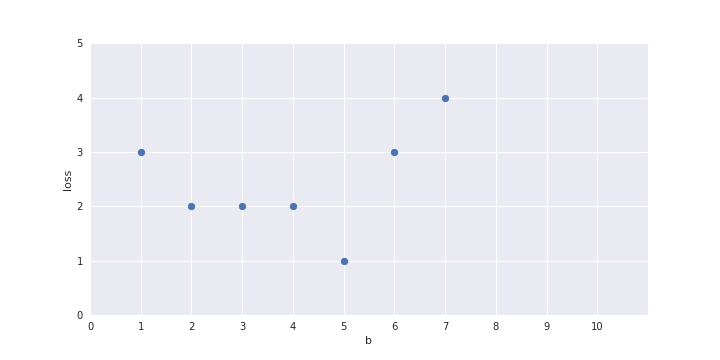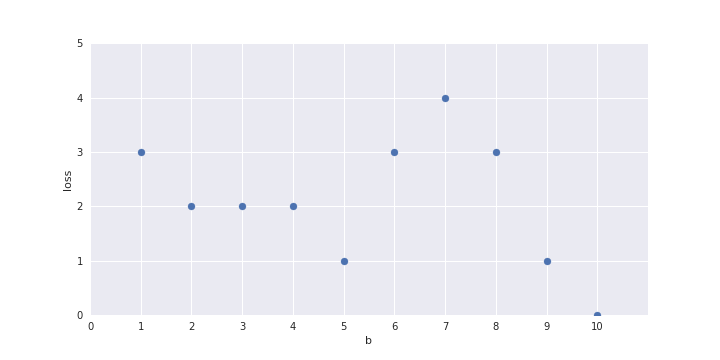
| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| Like? (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| prediction | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Evaluation
How does MP perform?
(c) One Fourth Labs

| Launch (within 6 months) | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| Weight (<160g) | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Screen size (<5.9 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| dual sim | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| Internal memory (>= 64 GB, 4GB RAM) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| NFC | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| Radio | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Battery(>3500mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| Price > 20k | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| Like? (y) | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| predicted | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |

| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
Training data
Test data
Geometric Interpretation
How to interpret the model of MP neuron gemoetrically?
(c) One Fourth Labs

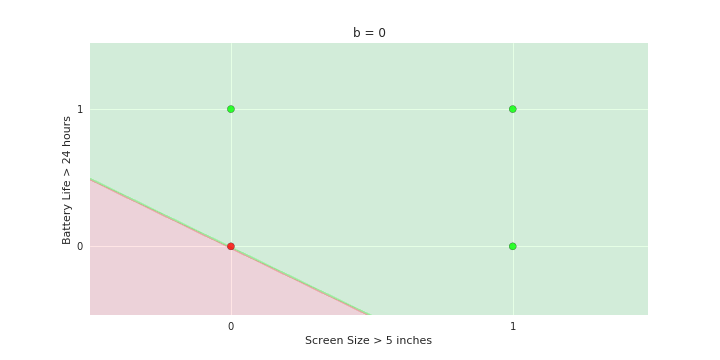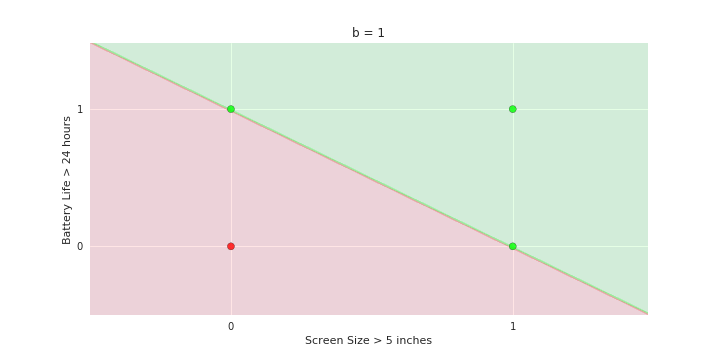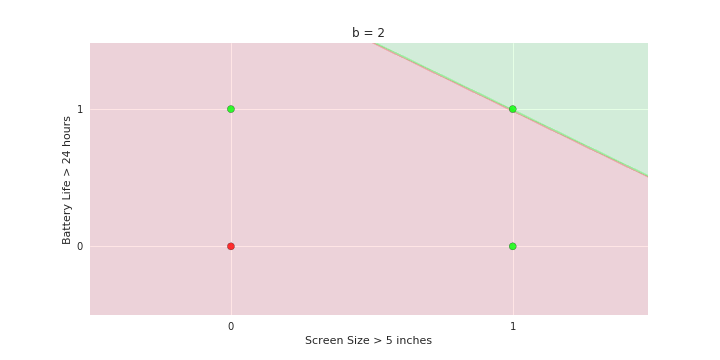
| Screen size (>5 in) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Battery (>2000 mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| Like | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |










Geometric Interpretation
How to interpret the model of MP neuron gemoetrically?
(c) One Fourth Labs

| Screen size (>5 in) | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| Battery (>2000mAh) | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| Like | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
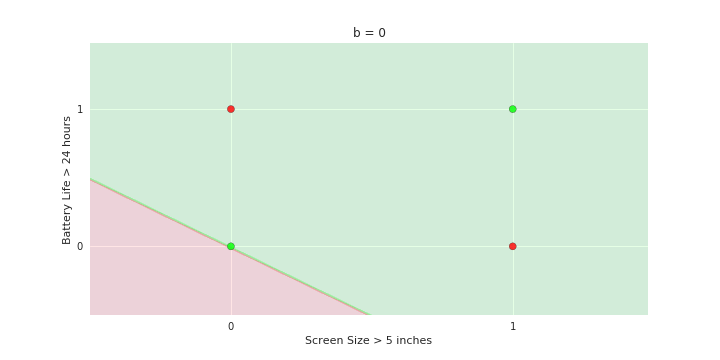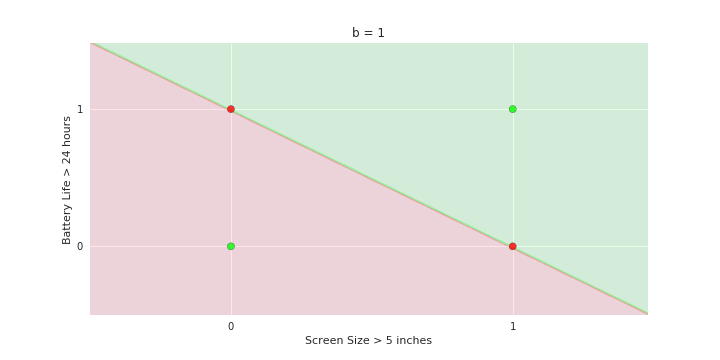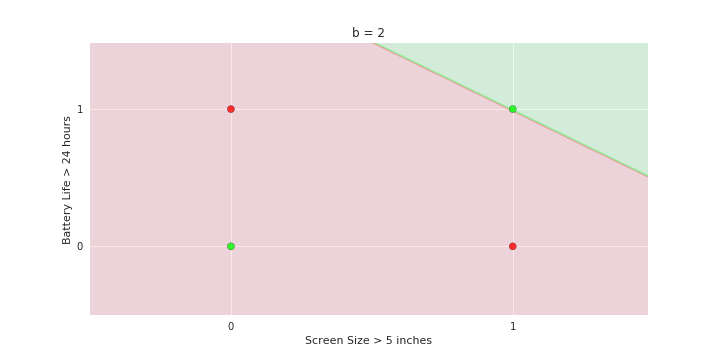
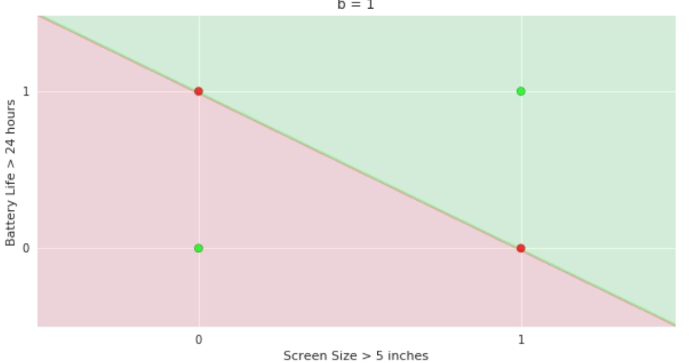
Linear
Fixed Slope
Few possible intercepts (b's)










Take-aways
So will you use MP neuron?
(c) One Fourth Labs

\( \{0, 1\} \)
Boolean







Loss
Model
Data
Task
Evaluation
Learning
Assignment
So will you use MP neuron?
(c) One Fourth Labs

Background of MP neuron
Understood model
Understood implications for data+task and loss function, learning algo
Understood the geometric interpretation to see that MP neuron cannot model complex relations
In the real world, data is not binary and relations are more complex
Hence this course continues
Will a binary search algorithm work?
Copy of Ananya's Copy of 1.5 McCulloch Pitts Neuron
By aakritibudhraja
Copy of Ananya's Copy of 1.5 McCulloch Pitts Neuron
- 766

