Local Composition Models
CHE 2101 - Spring 2022
April 21, 2022
Reference material: Rowley chapters 5 and 9
Lecture 25
van der Waals Mixture Partition Function
Learning Objective
Partition functions are normalization constants
Expectation values of some property
\left\langle J \right\rangle = \sum\limits_k \frac{J_k e^{-\beta U_k}}{Q}
J
Semi-classical partition function
Q = \frac{Z q_{int}^N}{N! \Lambda^{3N}}
What is the meaning of each term?
\frac{q_{int}}{\Lambda^{3}}
Molecular partition function
Q
System partition function
N!
Indistinguishability of molecules
Z
Configurational partition function
Partition functions review
Configurational partition function
That makes sense, right?
Z = \int \cdots \int e^{-\beta U} dq^{3N}
Not to me
Partition functions review
Configurational partition function - Toy system
Angle-averaged interaction energy of water dimer (HW 7)
e^{-\beta U}
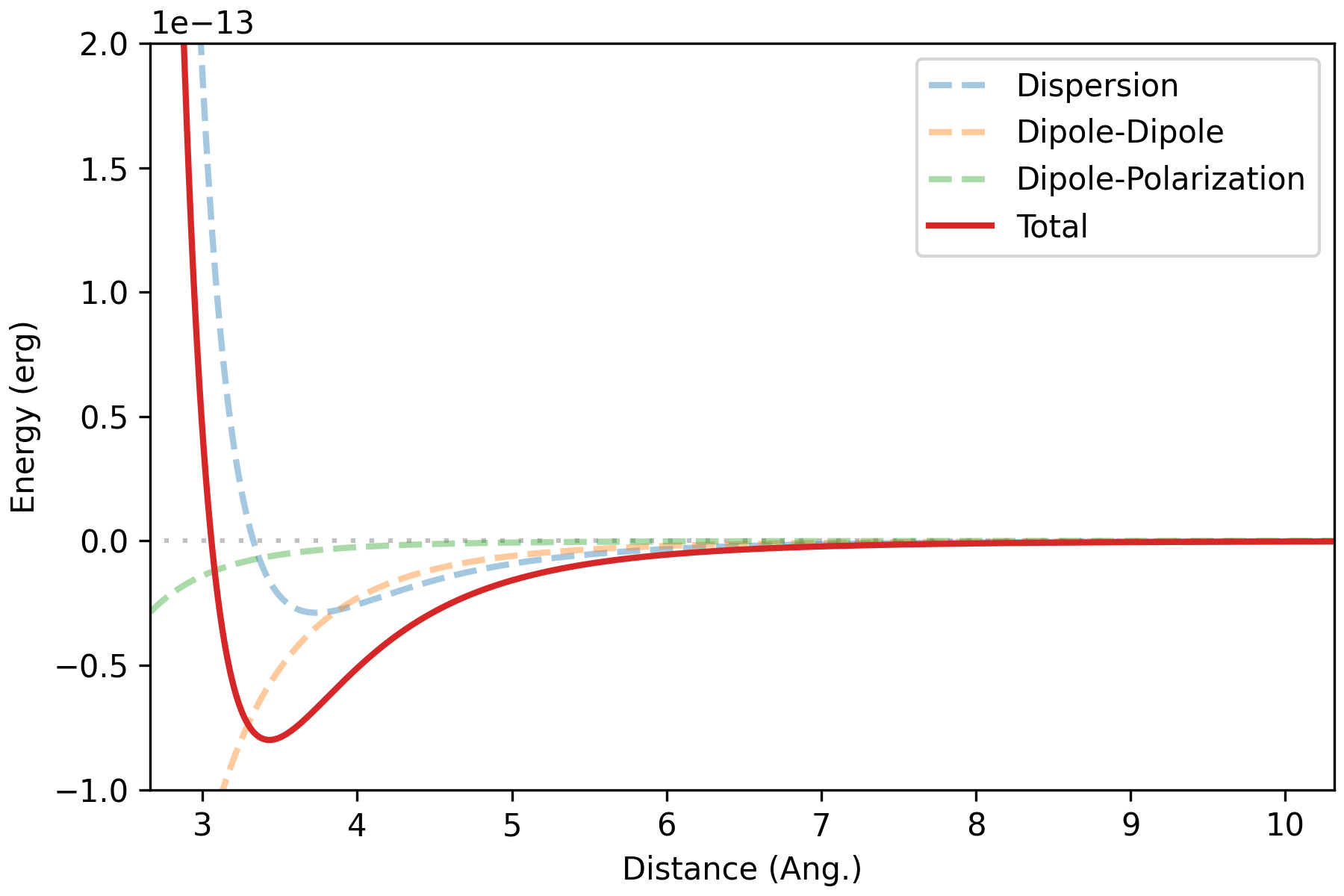
T = 298.15 # K
beta = 1/(kB * T) # 1/erg
bolz_factor = np.exp(-beta*u_total)
Z = np.sum(bolz_factor) # 116691.201
prob = bolz_factor/Z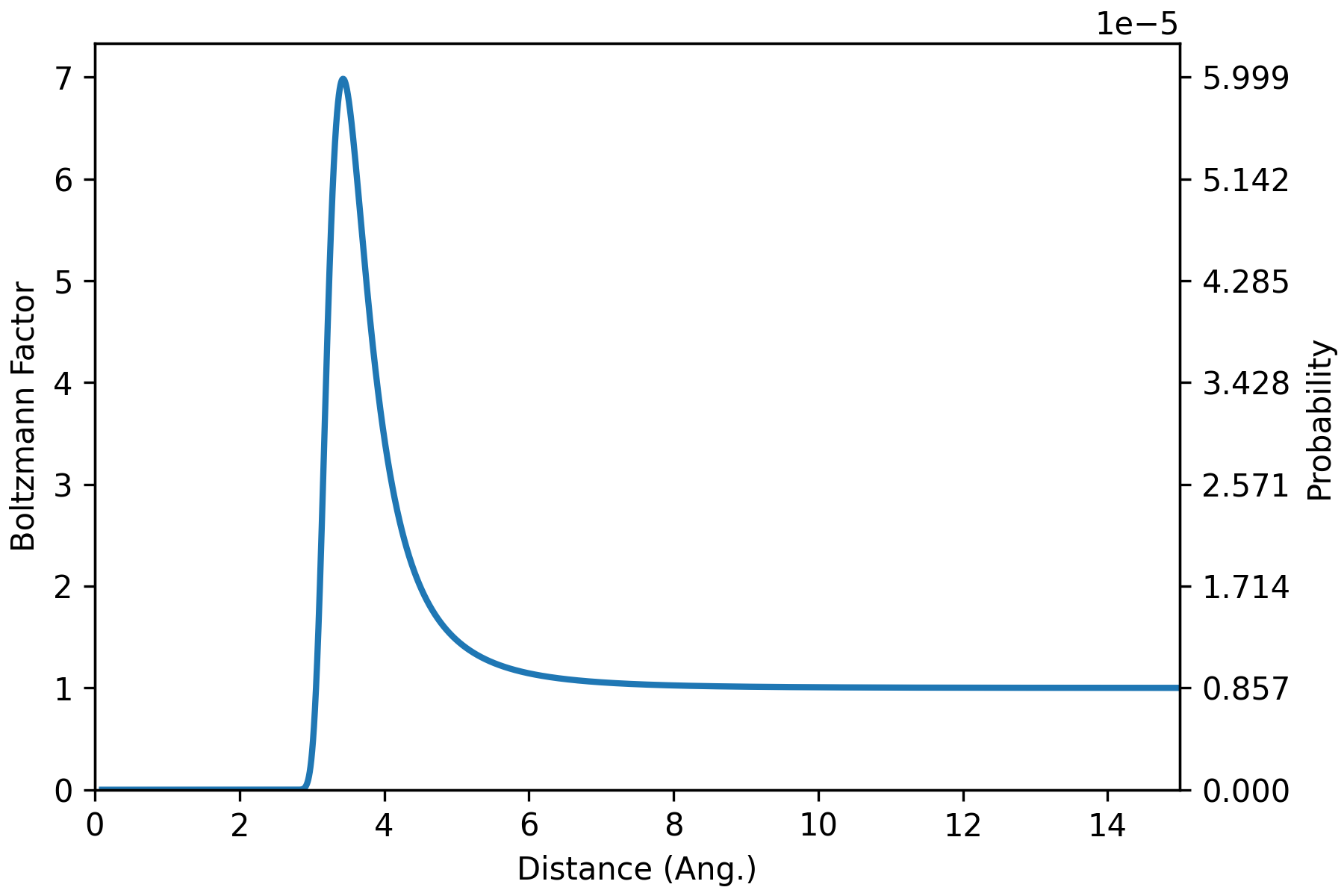
Z = \int \cdots \int e^{-\beta U} dq^{3N}
dq^{3N} = dr
Partition functions review
Partition functions review
Z for real systems would have 3N dimensions
Approximations are needed for analytical expressions
Configurational partition function - Real systems
For example: van der Waals partition function
Approximations/Approach
- Liquid molecules constrained in "lattice" cages
- Total potential energy is pairwise additive
- Mean-field pairwise potential
- No correlation between cages
Review from lecture 20
Partition functions review
Conceptualizing vdW framework
Lattice cage confining some molecule
Molecules do not respond to the motion of neighbors
(i.e., no correlation)
Review from lecture 20
Partition functions review
vdW partition function
Z_{vdW} = V_f^N \exp \left( - \frac{N u_0}{2 k_B T} \right)
V_f = \left[ \frac{4 \pi (a_1 - d)^3}{3} \right]
- Free volume: Cage volume accessible to the center of the hard sphere
- Two parameters
- The exponential term is the lattice potential contribution
- The potential energy of a molecule exploring its cage
Q_{vdW} = \frac{Z_{vdW} q_{int}^N}{N! \Lambda^{3N}}
a_1
d
Lattice information
Molecular diameter
u_0
Averaged lattice potential
Review from lecture 20
Takeaways
- Analytical expressions for Z are challenging
- vdW partition functions provide a framework for approximating Z
I learned
this
You learned
this?
I learned
this
Alex
You
Helmholtz Free energy of Mixing
Learning Objective
Disclaimer: Assuming
\Delta A_{mix} (T, V) \approx \Delta G_{mix} (T, P)
Helmholtz free energy of mixing
Q_{vdW} = \frac{\left( q_{1, int} \right)^{N_1} \left( q_{2, int} \right)^{N_2}}{N_1! N_2! \Lambda_1^{3N_1} \Lambda_2^{3N_2}} V_f^N \exp \left( - \frac{N \beta u_0}{2} \right)
\Delta A_{mix} = A_{m} - A_1^0 - A_2^0\\
= -k_B T \ln \left( \frac{Q_m}{Q_1^0 Q_2^0} \right)
A = - k_B T \ln Q
- vDW partition function for mixtures
- , , all cancel leaving you with
q_{int}
N
\Lambda^{3N}
\Delta A_{mix} = -k_B T \ln \left( \frac{V_{f}^{N}}{V_{f, 1}^{N_1} V_{f, 2}^{N_2}} \right)
+ \frac{1}{2} \left( N u_0 - N_1 u_{0, 1} - N_2 u_{0, 2} \right)
\Delta A_{mix} =
\Delta A_{athermal}
\Delta A_{resid}
+
Entropic effects based on free volume differences
Energetic differences between like and unlike interactions
Calculating
\Delta A_{mix}
- Put final minus initial Helmholtz free energy in terms of partition functions
Helmholtz free energy of mixing
Possible assumption 1/2
Athermal contribution
Free volume is proportional to N
\Delta A_{atherm} = -k_B T \ln \left( \frac{V_{f}^{N}}{V_{f, 1}^{N_1} V_{f, 2}^{N_2}} \right)
\Delta A_{atherm} = - k_B T \ln \left( \frac{N^{N}}{N_1^{N_1} N_2^{N_2}} \right)
\Delta A_{atherm} = - k_B T \ln \left( \frac{N^{N_1 + N_2}}{(x_1 N)^{N_1} (x_2 N)^{N_2}} \right)
= k_B T \ln \left( x_1^{N x_1} x_2^{N x_2} \right)
= N k_B T \ln \left( x_1^{x_1} x_2^{x_2} \right)
Use
N_i = x_i N
Ideal mixture model
\Delta A_{atherm}^{id}
\Delta A_{atherm} = \Delta A_{atherm}^{id} + A_{atherm}^{E}
Would this be always positive, negative, or does it depend? Why?
Helmholtz free energy of mixing
Possible assumption 2/2
Athermal contribution
\Delta A_{atherm} = -k_B T \ln \left( \frac{V_{f}^{N}}{V_{f, 1}^{N_1} V_{f, 2}^{N_2}} \right)
\Delta A_{atherm} = -k_B T \ln \left( \frac{V_{m}^{N}}{V_{1}^{N_1} V_{2}^{N_2}} \right)
Define volume fraction as
= k_B T \ln \left( \frac{V_1^{N_1} V_2^{N_2}}{V_m^{N_1} V_m^{N_2}} \right)
\phi_i = V_i / V_m
= k_B T \ln \left( \phi_1^{N_1} \phi_2^{N_2} \right)
= k_B T \left[ N_1 \ln \left( \phi_1 \right) + N_2 \ln \left( \phi_2 \right) \right]
Flory-Huggins Equation
Free volume if proportional to molar volume
V_{f, i} \propto V_i
Helmholtz free energy of mixing
Residual contribution
Direct expressions are rare, so we use this instead
\Delta A_{resid} =\frac{1}{2} \left( N u_0 - N_1 u_{0, 1} - N_2 u_{0, 2} \right)
\Delta A_{resid} = T \int\limits_0^{1/T} \Delta U_{resid} \; d \left( \frac{1}{T} \right)
Easy, right?
Local composition models can accomplish this
Now we just need to find
\Delta U_{resid}
Ehh
Takeaways
- Use vdW partition function for Helmholtz free energy of mixing
- Ways to compute the athermal contribution
- Can use local composition models for residual contribution
I learned
this
You learned
this?
I learned
this
Alex
You
Local composition models
Learning Objective
Disclaimer: Assuming
\Delta A_{mix} (T, V) \approx \Delta G_{mix} (T, P)
Review: Pair correlation function
Configurational integrals for real systems are challenging
Relative probability of finding a second molecule some distance away
Pair correlation function ( ) is a proxy for configurational information
g
1
Distance
g
Coordnation shells
Review from lecture 20
Review: Pair correlation functions
Number of neighboring molecules
d N_r = \rho g (r) \; d \bold{r}
Differential number of atoms in a shell r distance away
is the numerical density of the system
\rho
is a volume element
d \bf{r}
d \bold{r} = \int\limits_0^{2 \pi} \int\limits_0^\pi r^2 \sin \theta \; d \theta \; d \phi \; dr = 4 \pi r^2 \; dr
= 4 \pi r^2 \rho g (r) \; dr
Total number of atoms within a distance r
N (r) = 4 \pi \rho \int\limits_0^r r^2 g (r) \; dr
What happens if we integrate to ?
\infty
Review from lecture 20
Local composition models
Computing local compositions
N_{21} = 4 \pi \rho_2 \int\limits_0^L g_{21} (r) r^2 \; dr
N_{12} = 4 \pi \rho_2 \int\limits_0^L g_{12} (r) r^2 \; dr
x_{21} = \frac{N_{21}}{\sum\limits_k N_{k1}} = \frac{4}{6}
Type 1
Type 2
Number of type 2 moleucles around type 1
Number of type 1 moleucles around type 2
x_{12} = \frac{N_{12}}{\sum\limits_k N_{k2}} = \frac{4}{6}
Local composition models
Computing local compositions
x_{11} = \frac{4 \pi \rho_1 \int\limits_0^L g_{11} (r) r^2 \: dr}{4 \pi \rho_1 \int\limits_0^L g_{11} (r) r^2 \: dr \; + \; 4 \pi \rho_2 \int\limits_0^L g_{21} (r) r^2 \: dr}
We can use radial distribution functions to compute local mole fractions
For example, the mole fraction of type 1 molecules around another type 1
Local composition models
Computing local compositions
G_{21} = \frac{4\pi \int\limits_0^L g_{21} (r) r^2 \; dr}{4\pi \int\limits_0^L g_{11} (r) r^2 \; dr}
We can simplify this expression by considering differences in random mixing
Probability ratio of finding type 2 molecules over type 1
Example: 50:50 mixture
N_2 = N_1
N_2 > N_1
N_2 < N_1
G_{21} = 1
G_{21} > 1
G_{21} < 1
Number of neighboring molecules
Mixing factor
x_{11} = \frac{x_1}{x_1 + x_2 G_{21}}
x_{21} = \frac{x_2 G_{21}}{x_1 + x_2 G_{21}}
x_{11} = \frac{4 \pi \rho_1 \int\limits_0^L g_{11} (r) r^2 \: dr}{4 \pi \rho_1 \int\limits_0^L g_{11} (r) r^2 \: dr \; + \; 4 \pi \rho_2 \int\limits_0^L g_{21} (r) r^2 \: dr}
Local composition models
Circling back to
We can now estimate using this concept of nonrandom mixing factors
\Delta A_{resid}
\Delta A_{resid}
Wilson Model
Assumptions
- Potentials of mean force are used instead of pair potentials
- Shell thickness is the first coordination shell
\Delta U_{resid} = x_1 x_2 \left[
\frac{\left( \left\langle u \right\rangle_{21} - \left\langle u \right\rangle_{11} \right) G_{21}}{x_1 + x_2 G_{21}}
+ \frac{\left( \left\langle u \right\rangle_{12} - \left\langle u \right\rangle_{22} \right) G_{12}}{x_2 + x_1 G_{12}}
\right]
A_{resid}^E = - RT \left[ x_1 \ln \left( x_1 + x_2 G_{21} \right) + x_2 \ln \left( x_2 + x_1 G_{12} \right)\right]
G_{ji} = \frac{V_{j}}{V_{i}} \exp \left[ - \frac{\lambda_{ij}}{RT} \right]
\lambda_{21} = \left\langle u \right\rangle_{21} - \left\langle u \right\rangle_{11}
Disclaimer: Assuming
\Delta A_{mix} (T, V) \approx \Delta G_{mix} (T, P)
Local composition models
Circling back to
\Delta A_{resid}
Nonrandom two-liquid (NRTL) model
Introduces nonrandom mixture parameters
G_{ij} = \exp \left( - \frac{\alpha a_{ij}}{RT} \right)
\alpha
a_{ij}
A_{resid}^E = RT x_1 x_2 \left( \frac{\tau_{21} G_{21}}{x_1 + x_2 G_{21}} + \frac{\tau_{12} G_{12}}{x_2 + x_1 G_{12}} \right)
Disclaimer: Assuming
\Delta A_{mix} (T, V) \approx \Delta G_{mix} (T, P)
Local composition models
Activity coefficients
Both local models can compute acitivty coefficients
ln \left( \lambda_{1} \right) = - \ln \left( x_1 + x_2 G_{21} \right) - x_2 \left( \frac{G_{12}}{x_2 + x_1 G_{12}} - \frac{G_{21}}{x_1 + x_2 G_{21}} \right)
Wilson
NRTL
ln \left( \lambda_{1} \right) = x_2^2 \left[ \tau_{21} \left( \frac{G_{21}}{x_1 + x_2 G_{21}} \right)^2 + \frac{\tau_{12} G_{12}}{\left( x_2 + x_1 G_{12} \right)^2} \right]
Takeaways (final)
- Pair correlation functions are a proxy for configurational information
- Deviations in spatial compositions provide information on nonideal mixing
- Local models can be used to compute activity coefficients and energy of mixing
I learned
this
You learned
this?
I learned
this
Alex
You
Local composition models
By aalexmmaldonado
