The race to demonstrate quantum supremacy, and onward to quantum computers
Abdullah Khalid
Quantum Information Scientist
HUAIC
5th November 2019

Computational Problems



Decision
Search
Optimization
Decision Problems
Multiplication
Input: integers P and Q
Output: integer R = P x Q


Algorithms
Is left most digit 1 in binary?
Decision Problems
Factorization
Input: integer R
Ouput: prime numbers P and Q
such that R = P x Q
Algorithms
R = 21
digits = 2
R = 498556150811
digits = 12
- Dixon's algorithm
- Continued fraction factorization
- Quadratic sieve
- Rational sieve
- General number field sieve
- Shanks's square forms factorization

Is left most digit of bigger prime 1 in binary?
Cryptography

"Top secret info"
"Top secret info"
"hf72h18v82ja9"
You
You
Military
Bank
Email provider
Military
Sampling Problems
Binomial sampling
Input: n, p
Output: a sample from the binomial probability distribution
A random number generator

Extended Church-Turing Thesis [1]
Any algorithmic process can be simulated efficiently using a probabilistic Turing machine.
Church-Turing Thesis
Any algorithmic process can be computed using a Turing machine.
[1] They didn't actually say it.
Physicist's Extended Church-Turing Thesis
Every finitely realizable physical system can be perfectly simulated by a universal computing machine operating by finite means - Deutsch 1985



Chemistry
Biology
Computer science
Computing Machine = Physical System
Computing Machines = Physical Systems
=> Computational complexity is determined by physical laws

Computational Complexity
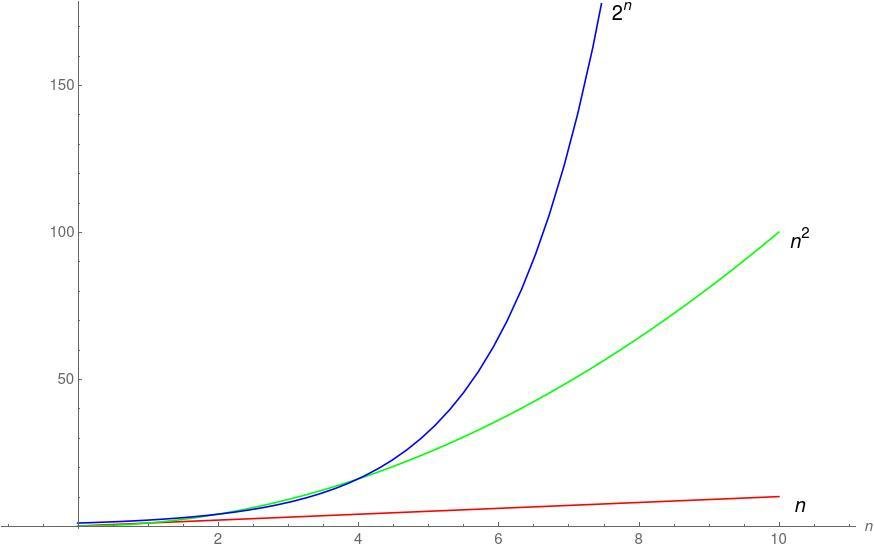
Multiplication
Factorization
Resources
Problem size (n)

Decision Problems Complexity Classes
Factoring
Multiplication
Circuit model of classical computation

Width/Space = n
Depth/Time = m
Input: Any of 2n n-bit strings
Output: 1-bit string
Quantum Computers


Quantum Circuits
Text
Text
n-qubits => 2n outcomes
- Solves same computational problems as classical computer
- Algorithm is different because of architecture difference



Quantum Computers: The transport analogy
Human computer
Super computer
Quantitative
Qualitative
Quantum computer
Solve computational problem = Go from A to B
Quantum computers CANNOT
do industrial optimization
predict the stock market
optimize airline schedules
predict the stock market
optimize airline schedules
NP-Complete problems
exponentially faster than classical computers.

If this was true, quantum computers could solve NP-complete problems efficiently
But they don't!
Quantum computers can
simulate atoms, molecules and materials,
exponentially faster than classical computers.

Quantum computers can
maybe do machine learning and optimization
exponentially faster than classical computers.

Quantum computers can
break all currently used asymmetric encryption protocols
exponentially faster than classical computers.

Quantum vs Classical Computers

Breaking encryption on Quantum Computer
Text
NP-Complete Problems on Classical/Quantum Computer
Breaking encryption on Classical Computer
Resources
Problem size (n)

Decision Problems Complexity Classes
BQP (bounded-error quantum polynomial time )
= set of problems efficiently solvable by a quantum computer
Quantum computers difficult to build due to engineering challenges


Nature | Vol 574 | 24 OCTOBER 2019
| Quantum Supremacy | Quantum Advantage | |
|---|---|---|
| A devices that: | Solves any problem faster than classical | Solves useful problems faster than classical |
| Requires | Non-universal quantum computational device | Universal Quantum Computer |
| Quantum error correction | ||
| Analogies | Fission experiments | Nuclear power stations |
| Wright brothers flight | Commercial/military airplanes |

Depth/Time = m
Width/Space = n
Quantum Random Circuit
Outputs = 2n Output strings, each with different probability
Form a random circuit using √ X , √ Y , √ W , and a combination of iSWAP and C-Z.
,
Quantum Random Circuit

Computation problem
Input: Circuit C
Output: a sample from the output probability distribution of C
Easy for quantum computer
Difficult for classical computer

Google's superconducting chip
53+1 qubits, depth = 20
How to verify a device which you claim can't even be classically simulated?
Linear cross-entropy benchmarking fidelity
- Collect finite samples x1, x2, x3, ...
- Calculate probabilities P(xi) of measuring xi given circuit C
- Calculate FXEB = 2n Avg(P(xi)) - 1
FXEB = 0 => uniform random distribution
FXEB = 1 => error-free quantum random circuit

Verification that device works
Is quantum supreme?
Google's claim: 10,000 years on a state of the art supercomputer, using the best classical algorithm they could think of.
IBM's claim: Sorry, 2.5 days only using our better classical algorithm!
Quantum device performance: 600 seconds to sample 3 million times
The race to demonstrate quantum supremacy, and onward to quantum computers
By abdullahkhalids
The race to demonstrate quantum supremacy, and onward to quantum computers
- 2,124



