Levenshtein
(Edit)
DISTANCE
Algorithm
ABDULLAH ALSHAMMRI
overview
- What is it !?
-
Applications and Usages.
- How it works?
- Example and demo.
-
Complexity.
- Implementation.
- References.
EDIT DISTANCE
-
Measures the similarity between two strings.
- Test is similar to Text
- By replacing ONE character s with x , it becomes the same
-
Levenshtein
is the name of a Russian scientist Vladimir Levenshtein who invented the
algorithm in 1965.
- It is a Dynamic Programming Algorithm.
Applications and usages
- Spell Checkers
- TRST => Do you mean Test?
- DNA Analysis
- Used among other algorithms
- It used in LCS, Longest Common Subsequence.
- I was going to discuss LCS, however, I found LCS depends on Edit Distance.
- LCS useful with File Comparison.
- Refer to the reference in the last slide for more information about LCS.
- Linux diff app depends on LCS witches depends on Edit Distance.
How IT WORKS?
-
S1 is the first string and m is its length.
-
S2 is the second string and n is its length
-
if n==0 return m and exit
-
if m==0 return n and exit
-
create new 2d array called distance
- fill first row (0,1,2...to n) and fill first column (0,1,2,.. to m)
-
and for each distance[i][j] do :
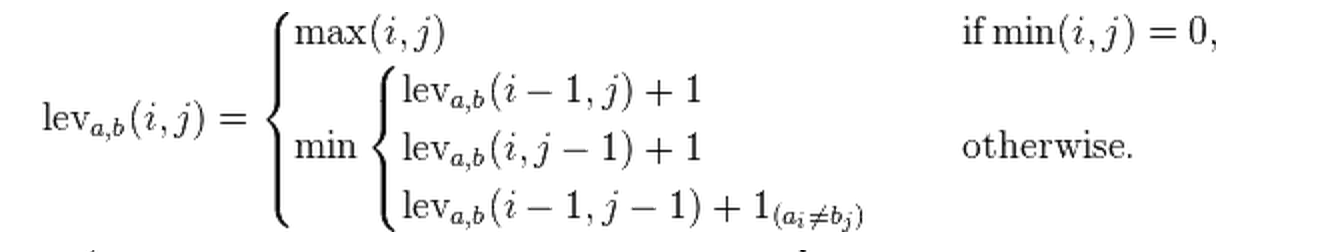
- The distance ( minimal operation needed ) is distance[n][m]
Example
|
|
j=0
|
j=1
|
j=2
|
j=3
|
j=4
|
j=5
|
|
|
|
#
|
E
|
X
|
I
|
T
|
|
i=0
|
#
|
0
|
1
|
2
|
3
|
4
|
|
i=1
|
E
|
1
|
|
|
|
|
|
i=2
|
X
|
2
|
|
|
|
|
|
i=3
|
I
|
3
|
|
|
|
|
|
i=4
|
S
|
4
|
|
|
|
|
|
i=5
|
T
|
5
|
|
|
|
|
|
i=6
|
S
|
6
|
|
|
|
|
Example
|
|
j=0
|
j=1
|
j=2
|
j=3
|
j=4
|
j=5
|
|
|
|
#
|
E
|
X
|
I
|
T
|
|
i=0
|
#
|
0
|
1
|
2
|
3
|
4
|
|
i=1
|
E
|
1
|
0 |
1 |
2 |
3 |
|
i=2
|
X
|
2
|
|
|
|
|
|
i=3
|
I
|
3
|
|
|
|
|
|
i=4
|
S
|
4
|
|
|
|
|
|
i=5
|
T
|
5
|
|
|
|
|
|
i=6
|
S
|
6
|
|
|
|
|
Example
|
|
j=0
|
j=1
|
j=2
|
j=3
|
j=4
|
j=5
|
|
|
|
#
|
E
|
X
|
I
|
T
|
|
i=0
|
#
|
0
|
1
|
2
|
3
|
4
|
|
i=1
|
E
|
1
|
0 |
1 |
2 |
3 |
|
i=2
|
X
|
2
|
1 |
0 |
1 |
2 |
|
i=3
|
I
|
3
|
|
|
|
|
|
i=4
|
S
|
4
|
|
|
|
|
|
i=5
|
T
|
5
|
|
|
|
|
|
i=6
|
S
|
6
|
|
|
|
|
Example
|
|
j=0
|
j=1
|
j=2
|
j=3
|
j=4
|
j=5
|
|
|
|
#
|
E
|
X
|
I
|
T
|
|
i=0
|
#
|
0
|
1
|
2
|
3
|
4
|
|
i=1
|
E
|
1
|
0 |
1 |
2 |
3 |
|
i=2
|
X
|
2
|
1 |
0 |
1 |
2 |
|
i=3
|
I
|
3
|
2 |
1 |
0 |
1 |
|
i=4
|
S
|
4
|
3 |
2 |
1 |
1 |
|
i=5
|
T
|
5
|
4 |
3 |
2 |
1 |
|
i=6
|
S
|
6
|
5 |
4 |
3 |
2 |
Example
So The minimum operations needed to convert EXISTS to EXIT is 2
2 here is two deletion operations
EXISTS => EXIT
COMPLEXITY
- It's a Dynamic Programming paradigm , each iteration depends on the last operation to solve the current one.
- Time Complexity is Big O(MN) , or O(MN+M+N)
- Space Complexity is a 2D array O(MN)
- N and M is the length of tow strings S1 and S2
- Brute Force version is very complex
- HELLO and XXXXX needs more than 2523 STEPS to finish
- However , the Dynamic Programming version need +35 STEPS.
IMPLEMENTATION
REFERENCES
-
Levenshtein, Vladimir I. (February 1966). "Binary codes capable of
correcting deletions, insertions, and reversals". Soviet Physics Doklady.
-
Hirschberg, D. S. (1975). "A linear space algorithm
for computing maximal common subsequences". Communications of the ACM .
-
Levenshtein distance , http://en.wikipedia.org/wiki/Levenshtein_distance
THANKS
Levenshtein (Edit) Distance Algorithm
By abshammeri
