Comet.ml
... and friends
Adam Getchell & Scott Kirkland
University of California, Davis
Data Science Initiative
GitHub for Machine Learning
Demo
Numerical Quantum Gravity
... in 3 easy steps
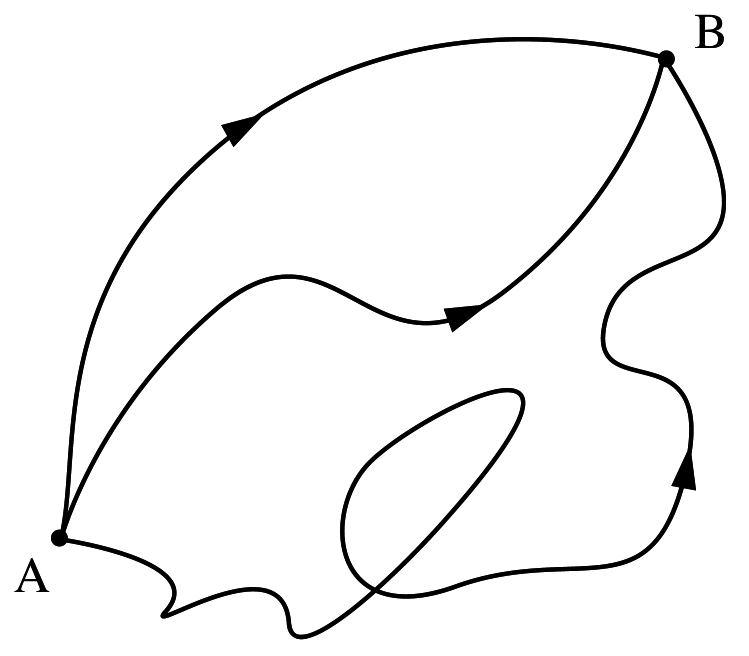
Path Integral
\langle B|T|A\rangle=\int\mathcal{D}[g]e^{iI_{EH}}
I_{EH}=\frac{1}{16\pi G_{N}}\int d^{4}x\sqrt{-g}(R-2\Lambda)
Equations of Motion
\partial S = 0 \rightarrow R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=8\pi G_{N}T_{\mu\nu}
Ricci scalar
Cosmological constant
Ricci tensor
Ricci scalar
Stress-Energy tensor
Transition probability amplitude
Foliation
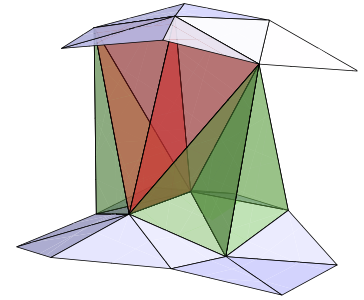
I_{R}=\frac{1}{8\pi G_{N}}\left(\sum\limits_{hinges}A_{h}\delta_{h}-\Lambda\sum\limits_{simplices}V_{s}\right)
Metropolis-Hastings
\langle B|T|A\rangle=\sum\limits_{triangulations}\frac{1}{C(T)}e^{-I_{R}(T)}
Inequivalent Triangulations
Partition Function
Wick rotation
- Pick an ergodic (Pachner) move
- Make that move with a probability of a1a2, where:
a_{1}=\frac{move[i]}{\sum\limits_{i}move[i]}
a_{2}=e^{\Delta S}
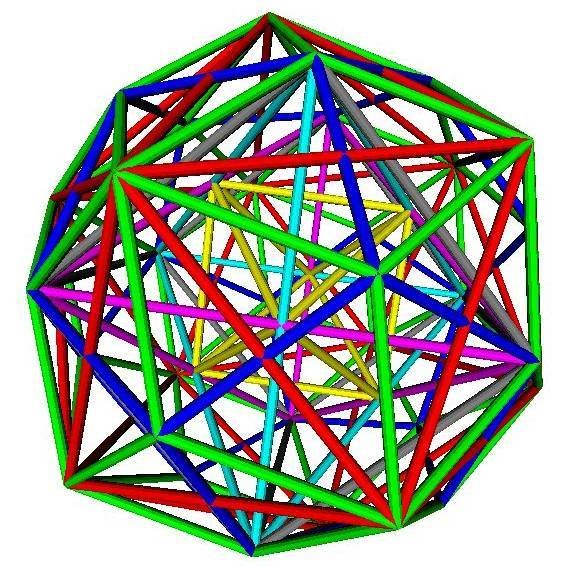
Fast foliated Delaunay Triangulations in CGAL
256 timeslices, 222,132 vertices, 2,873,253 faces, 1,436,257 simplices
Creation time: 284.596s
(MacBook Pro Retina, Mid 2012)
Demo
Comet.ml
By Adam Getchell
