Category Theory
A Category is:
- Some Objects
- Some Functions
- Some Laws
Who cares?
Motivations
People in the scala, f# and especially haskell world seem to use powerful but strange terminology and abstractions to build software.
What is that all about?
A comical example
-
1990 - A committee formed by Simon Peyton-Jones, Paul Hudak, Philip Wadler, Ashton Kutcher, and People for the Ethical Treatment of Animals creates Haskell, a pure, non-strict, functional language. Haskell gets some resistance due to the complexity of using monads to control side effects. Wadler tries to appease critics by explaining that "a monad is a monoid in the category of endofunctors, what's the problem?"
- from a brief and mostly wrong history of programming languages
A digression
1972 - Dennis Ritchie invents a powerful gun that shoots both forward and backward simultaneously. Not satisfied with the number of deaths and permanent maimings from that invention he invents C.
Who Cares
Scala + ScalaZ
a Scala library for functional programming
- Sum types
- Product types
- Functor
- Applicative
- Id
- Monoid
- so on
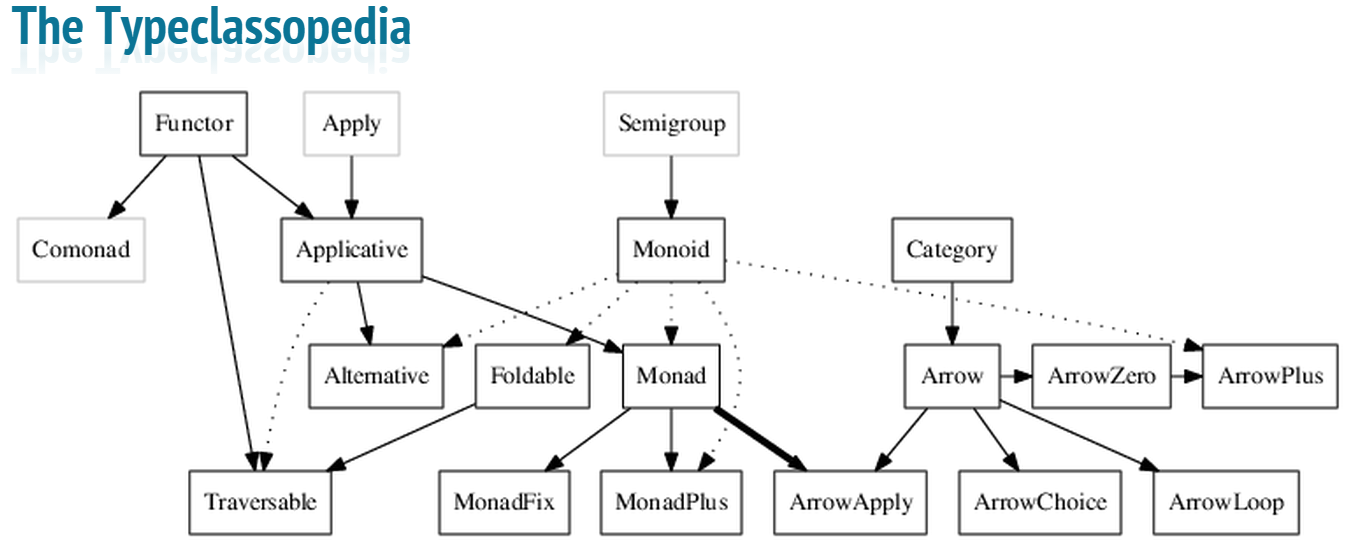
Examples
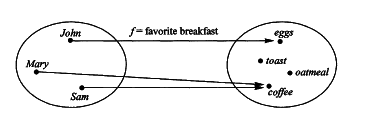
Examples
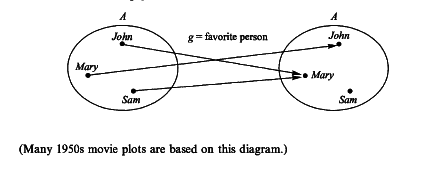
Examples
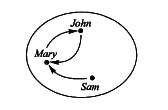
Examples

Examples

Category Theory is:
All about composition
Composition:
- f(g(x)) = f o g x
- o = composition operator
Some Laws:
- The Associative property
- f . (h . g) == (f . h) . g
- The Identity property
- There is a function that does nothing
- fi(a) = a
Addition Of Ints Category
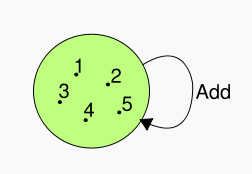
- 1 Object: Set of integers
- 1 function: Addition
Addition Of Ints Category

- Is this associative?
- Is there an identity function?
Addition Of Ints Category

- Is this associative?
- Yes 1 + (2+3) + (1+2) + 3
- Is there an identity function?
- it can be with the addzero function
- addzero(x) = x + 0
A Category is:
- Objects:
- A scala type ( and all its possible values)
- integers, doubles ...
- Functions
- These are normal functions and represent the arrows in our diagrams
- Laws
- some assumptions about the way things work
- ie. assositivity
A Category is:
-
ObjectsTypes - Functions
- Laws
A Category is:
- A way to reason about software using only the data types and function signatures
Monoids
- monoids are a category sometimes described as "string like"
- Once you learn about them, you will see them come up everywhere
Examples
- Lists
- Strings
- Numbers With Plus
- Numbers With Multiplication
Abstractions
In c#, java, scala we have an iterator interface, which exposes hasNext() and next() functions.
Common Interface
All things implementing the iterator interface can now be used equivalently, in for loops, and other library functions
Abstractions
A moniod interface can similarly be written. With 2 methods:
- mappend (monoidal append)
- zero (our identity function)
Common Interface
- All things implementing the monoid interface can now be used equivalently.
- The various monoids are quite differnt things, but can be treated the same.
- This is the power of abstraction Category Theory gives us.
- It is the power to notice related things and name them and abstract over them
Some cool monoid stuff
Some Examples
(go down)
Category Theory
By Adam Bell
Category Theory
- 957