Rust, For Science!
@adamisntdead
Rustfest Rome
\sum_{n=1}^{\infty} n= -\frac{1}{12}
∑n=1∞n=−121
\frac{\partial L}{\partial f} - \frac{d}{dt} \frac{\partial L}{\partial f'} = 0
∂f∂L−dtd∂f′∂L=0
\psi (x) = -i \hbar \frac{\partial}{\partial x}(-i \hbar \frac{\partial \psi}{\partial x})
ψ(x)=−iℏ∂x∂(−iℏ∂x∂ψ)
P(A \lvert B ) = \frac{P(B \lvert A) P(A)}{P(B)}
P(A∣B)=P(B)P(B∣A)P(A)
\sigma = \sqrt{\frac{\sum (x - \bar{x})^2}{n - 1}}
σ=n−1∑(x−xˉ)2
\nabla \times G = J + \frac{\partial D}{\partial t}
∇×G=J+∂t∂D
\rho (\frac{\partial V}{\partial t} + V\cdot \nabla V) = \nabla P + \rho g + \mu \nabla^2 V
ρ(∂t∂V+V⋅∇V)=∇P+ρg+μ∇2V
\hat{f}(\zeta) = \int_{-\infty}^{\infty} f(x) e^{-e \pi i x \zeta} dx
f^(ζ)=∫−∞∞f(x)e−eπixζdx
F_g = \frac{G m_1 m_2}{r^2}
Fg=r2Gm1m2
f(x) = \frac{1}{1 + e^{-x}}
f(x)=1+e−x1
J(\theta_j) \leftarrow 0_j \pm \eta \cdot \frac{\sum (\hat{y} - y)^2 \cdot x}{2n}
J(θj)←0j±η⋅2n∑(y^−y)2⋅x
\frac{d}{{dx}}f\left( x \right) = \mathop {\lim }\limits_{\Delta \to 0} \frac{{f\left( {x + \Delta } \right) - f\left( x \right)}}{\Delta }
dxdf(x)=Δ→0limΔf(x+Δ)−f(x)


@adamisntdead
github.com/adamisntdead
Adam Kelly
What is Scientific Computing?
High-Performance Computing
Data Science
Numerical Analysis & Simulation
Rust?


Let's Start Out With A Demo

What's Going On Here?
- Simulating a Double Pendulum
- Just plain Rust
- Uses a struct for state
- Displaying The Simulation
- Using
GGEZ - Takes values from the struct
- Using
Separate
Enter WebAssembly
pub struct DoublePendulumLagrangian {
/// Gravitational Constant.
pub g: f64,
/// Mass of the first bob.
pub m1: f64,
/// Mass of the second bob.
pub m2: f64,
/// Initial angle of the first bob.
pub t1: f64,
/// Initial angle of the second bob.
pub t2: f64,
/// Angular velocity of the first bob.
pub dt1: f64,
/// Angular velocity of the second bob.
pub dt2: f64,
/// Length of the rod for the first bob.
pub l1: f64,
/// Length of the rod for the second bob.
pub l2: f64,
}
impl DoublePendulumLagrangian {
// ...Enter WebAssembly
const { DoublePendulumLagrangian } = wasm_bindgen;
wasm_bindgen('../out/main_bg.wasm')
.then(runApp)
.catch(console.error)
function runApp() {
const elem = document.getElementById('container')
const two = new Two({ fullscreen: true })
.appendTo(elem)
const g = 9.8
const m1 = 2.0
const m2 = 2.0
const t1 = 2.0
const t2 = 1.5
const l1 = 100
const l2 = 100
const pendulum = DoublePendulumLagrangian.new(
g, m1, m2,
t1, t2, l1, l2
)
drawBobs(two, pendulum)
// ...The Results

Multithreading
Fearless Concurrency Makes Multithreading Easy
Sequential
Parallel
- Rayon
- Built-In threading
- OpenCL
- ArrayFire
Example: Numerical Integration
fn integrate<F>(f: F, a: f64, b: f64, n: u32) -> f64
where
F: Fn(f64) -> f64,
{
let h = (b - a) / n as f64;
let mut result = 0.5 * f(a) + 0.5 * f(b);
for i in 1..n {
result += f(a + i as f64 * h);
}
result * h
}Example: Numerical Integration
extern crate rayon;
use rayon::prelude::*;
Example: Numerical Integration
fn integrate_threaded<F>(f: F, a: f64, b: f64, n: u32) -> f64
where
F: Fn(f64) -> f64 + Sync,
{
let h = (b - a) / n as f64;
let result: f64 = (1..n)
.into_par_iter()
.map(|i| f(a + i as f64 * h))
.sum();
h * result
}Integrating With Standard Tools
Example 1: MPI
#include <mpi.h>
#include <stdio.h>
int main(int argc, char** argv) {
// Initialize the MPI environment
MPI_Init(NULL, NULL);
// Get the number of processes
int world_size;
MPI_Comm_size(MPI_COMM_WORLD, &world_size);
// Get the processes rank
int world_rank;
MPI_Comm_rank(MPI_COMM_WORLD, &world_rank);
// Get the name of the processor
char processor_name[MPI_MAX_PROCESSOR_NAME];
int name_len;
MPI_Get_processor_name(processor_name, &name_len);
// Print off a hello world message
printf("Processor %s, rank %d\n", processor_name, world_rank);
// Finalize the MPI environment
MPI_Finalize();
}Add The Dependency
[dependencies]
mpi = "0.5"Write in Rust
extern crate mpi;
use mpi::traits::*;
fn main() {
// Initialize the MPI environment
let universe = mpi::initialize().unwrap();
let world = universe.world();
// Get the number of processes
let size = world.size();
// Get the processes rank
let rank = world.rank();
// Get the processor name
let processor_name = mpi::environment::processor_name().unwrap();
// Print off a hello world message
println!("Processor {}, rank {}", processor_name, rank);
}Other Tools
- PyO3
- RGSL
- Rust Specific (
nalgebra , alga,nphysics , timely-dataflow, ...)
Interesting Developments
There are some new projects that look very promising.
Jupyter Notebooks

What about in Rust?
EXCVR
EXCVR
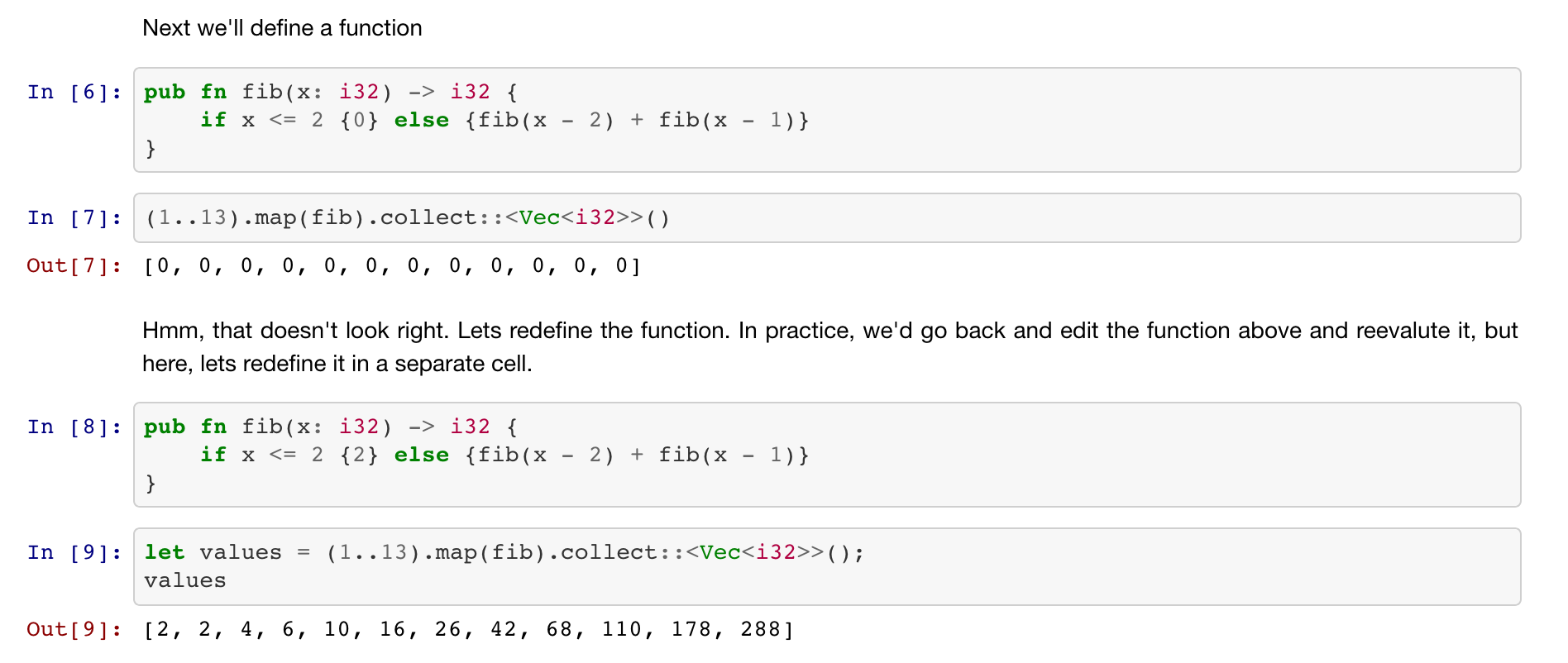
EXCVR
- Evaluation Context
- Jupyter Kernel
- REPL
So What's The Problem?
Resources
github.com/adamisntdead/rustfest-demos
github.com/google/evcxr
github.com/rustwasm
github.com/rust-unofficial/awesome-rust

Thank you!

@adamisntdead
github.com/adamisntdead
Adam Kelly
Rust, For Science!
By Adam Kelly
Rust, For Science!
- 575



