Benchmarking Deletion Metrics With The Principles Explanations
Contributions
Formalization of deletion metrics
New attribution function
Study OOD problem
Formalization of deletion metrics
Formalization
f: \mathbb{R}^d \longrightarrow \mathbb{R}
\begin{array}{lccc}
\varphi_f: & \mathbb{R}^d & \longrightarrow & \mathbb{R}^d \\
& x & \longmapsto & \psi \\
& \text{\tiny (image)} & & \text{\tiny(heatmap)}
\end{array}
The black-box model to study
Attribution function
(i) Delete the most relevant first: MoRF
Two evaluation scenarios of (and therefore of ):
\psi
\varphi_f
MoRF:
small AUC is better
nb area masked
Prediction
(ii) Delete the least relevant first: LeRF
small AUC is better
large AUC is better
Formalization
f: \mathbb{R}^d \longrightarrow \mathbb{R}
\begin{array}{lccc}
\varphi_f: & \mathbb{R}^d & \longrightarrow & \mathbb{R}^d \\
& x & \longmapsto & \psi \\
& \text{\tiny (image)} & & \text{\tiny(heatmap)}
\end{array}
The black-box model to study
Attribution function
Attribution rank
\sigma(\psi) = \text{\texttt{argsort}}(\psi)
(increasing order)
\text{MoRF}(\psi) = \sum_{k=0}^d f( x_{\setminus \sigma[k:]}) %= \sum_{k=0}^d f( x_{\sigma[:k]})
Evaluation function
Formalization
Remarks
(i) Deletion or Insertion is the same problem.
\text{MoRF}(\psi) = \sum_{k=0}^d f( x_{\setminus \sigma[k:]}) %= \sum_{k=0}^d f( x_{\sigma[:k]})
\text{MoRF}(\psi) = \sum_{k=0}^d f( x_{\setminus \sigma[k:]}) = \sum_{k=0}^d f( x_{\sigma[:k]})
(ii) logit vs proba
(iii) MoRF and LeRF are different problems
\text{LeRF}-\text{MoRF}(\psi) = \sum_{k=0}^d f( x_{\sigma[k:]}) - f( x_{\sigma[:k]})
max
min
Average
Treatment Effect?
Contributions
Formalization of deletion metrics
New attribution function
Study OOD problem
New attribution function
TRACE
Current Problem:
Too complicated and too vast.
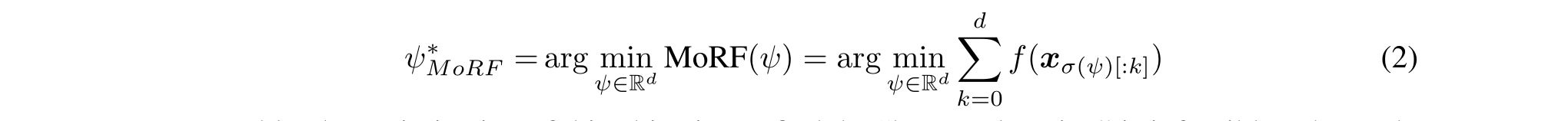
NP-hard
Let's convert the problem in into one in (permutations).
\mathbb{R}^d
\mathcal{S}_d
\mathcal{S}_d
is big ( ) but finite!
d!
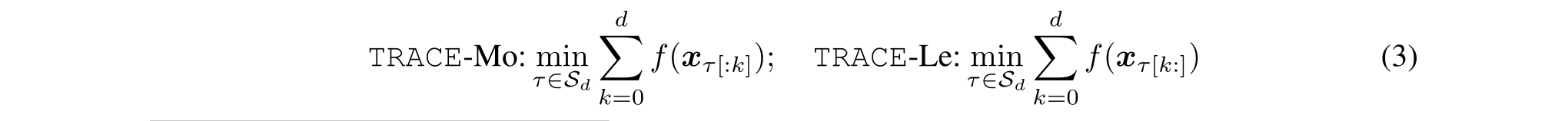
TRACE
for each k finds the set minimizing
f(x_{\setminus s_k})
Optimality
Greedy / SA
Global Optimum
(GO)
Complete Search
(CS)
\geq
\geq
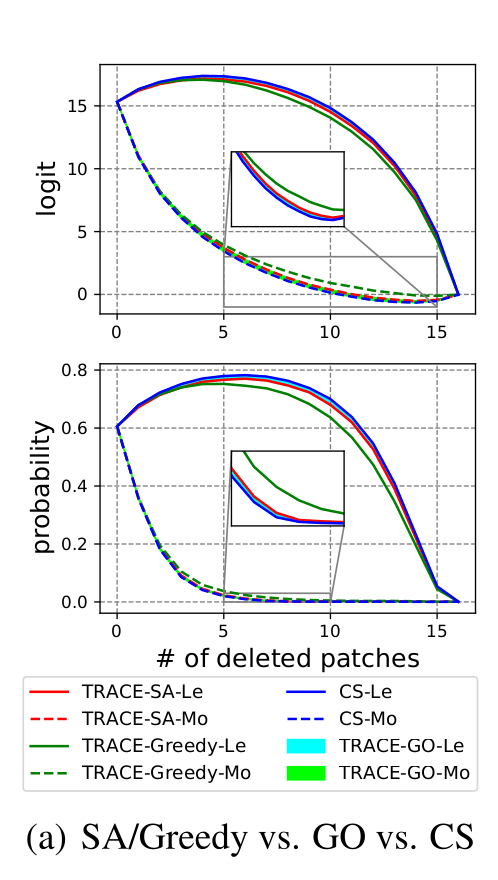
Algorithms
* patches instead of pixels
- Greedy
- Simulated Annealing (SA)
TRACE
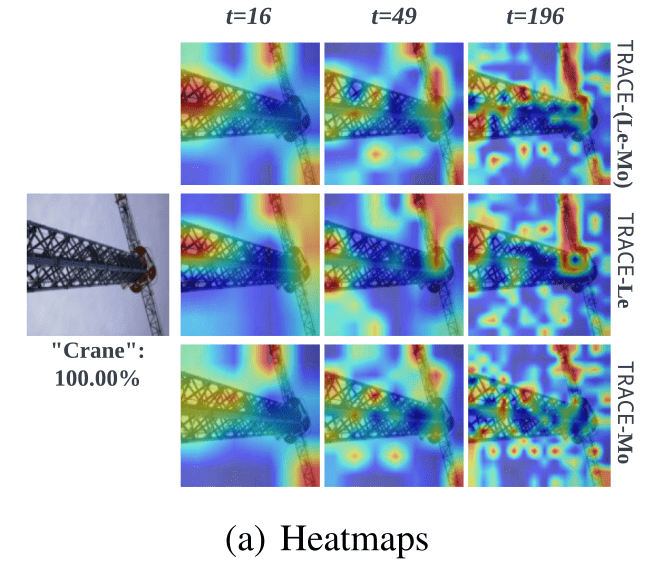
How order
is evaluated
How order
is computed
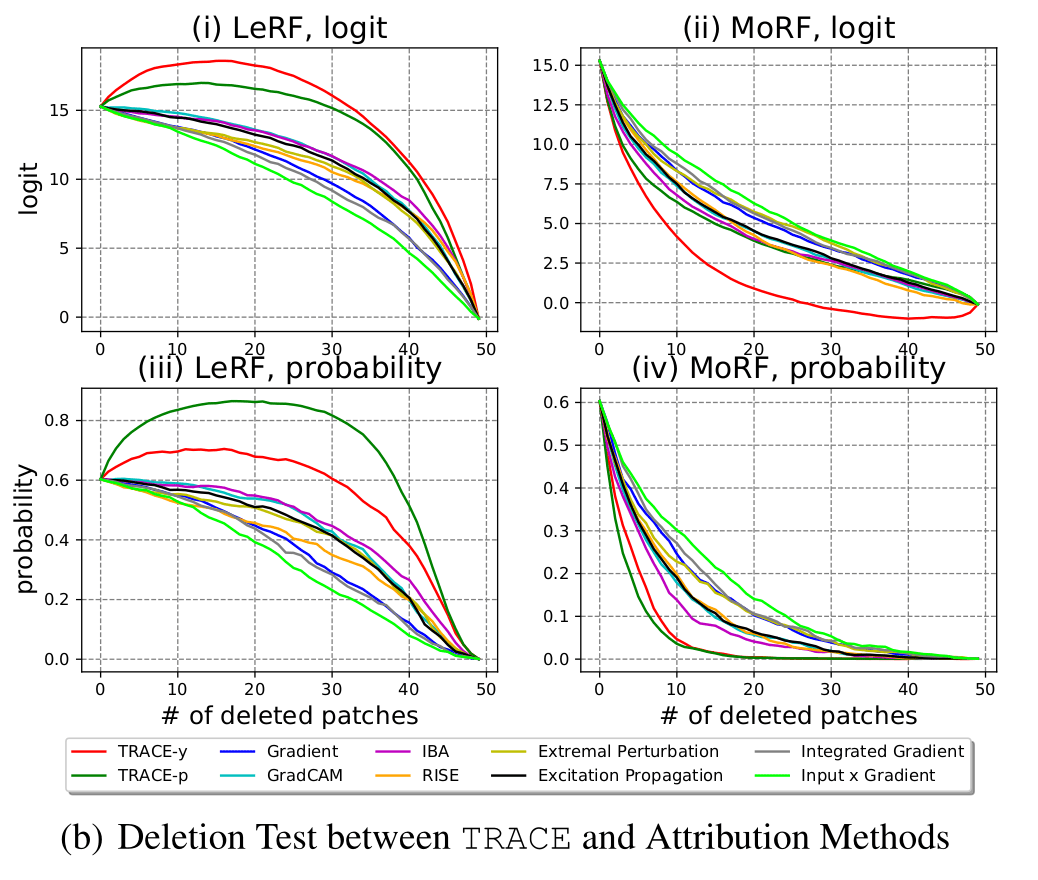
TRACE-Mo performs poorly in the LeRF test.
Recommendation for computing order
LeRF−MoRF > LeRF >> MoRG
TRACE-Mo performs poorly in the LeRF test.
TRACE-Le performs well in the MoRF test.
TRACE-Mo performs poorly in the LeRF test.
TRACE-Le performs well in the MoRF test.
TRACE-Le−Mo is most consistent in both tests.
Contributions
Formalization of deletion metrics
New attribution function
Study OOD problem
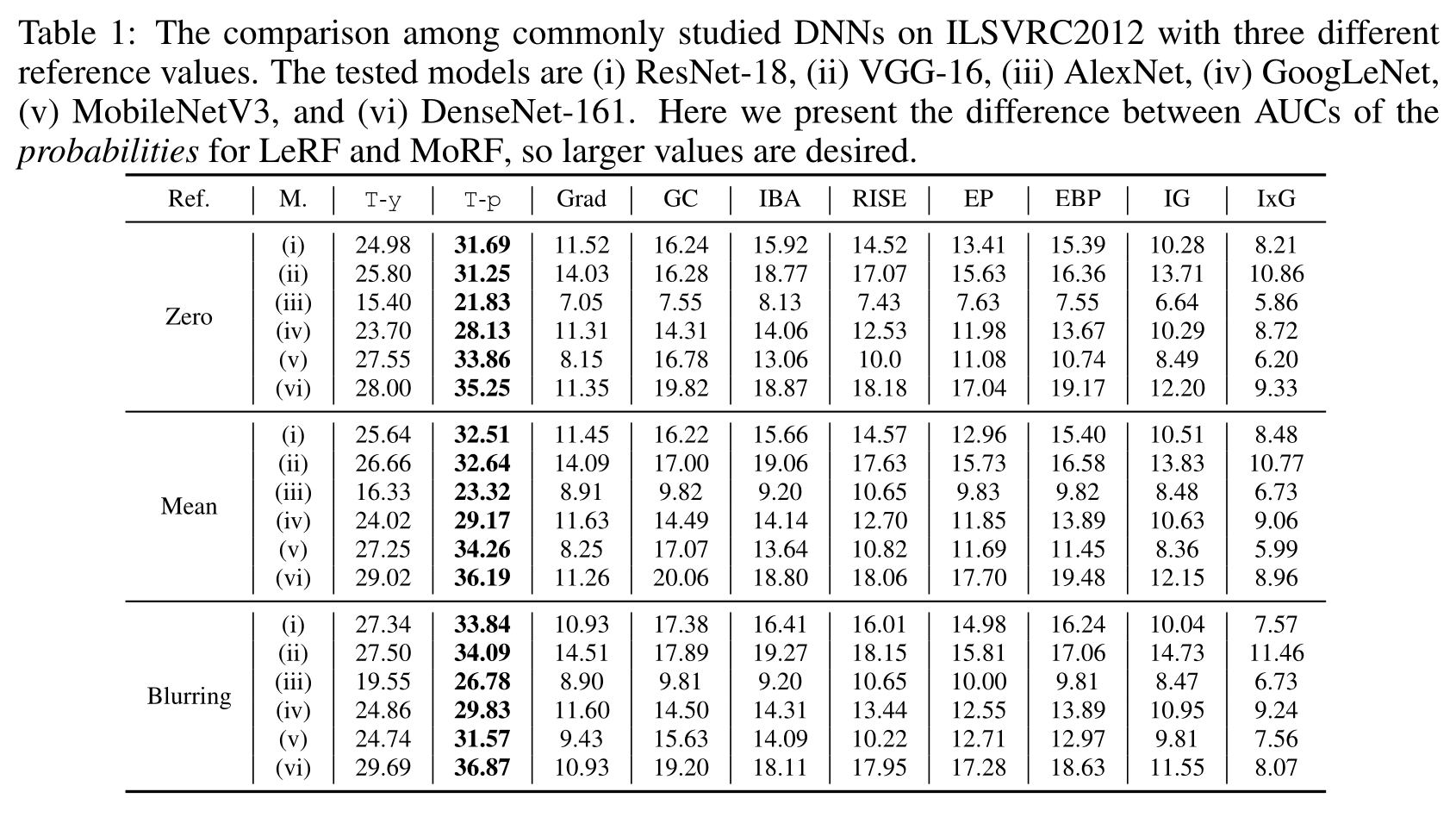
Study OOD problem
OOD Problem
Reference Value and OOD
Benchmarking Deletion Metrics With The Principles Explanations
BenchDelMet
By ahcene
