Ahcène Boubekki
Prototypes and
Self-Explainable Models
UCPH/Pioneer
From CNN to SEM
From CNN to SEM
Standard CNN Classifier
Self-Explainable Model
Centroid clustering ?
Conv.
Lin.Layer
Pool.
z
y
s
\phi
Prototypes
Simil.
Transparent
Classifier
y
y
CNN is an SEM
Ahcène Boubekki
Prototypes and
Self-Explainable Models
UCPH/Pioneer
From CNN to SEM
More prototypes
than classes?
Conv.
Lin.Layer
Pool.
z
y
y
but not a good one...
CNN is an SEM
Cross Entropy!
Not Obvious
Definitions
Properties
Definitions & Properties
Global Explanation
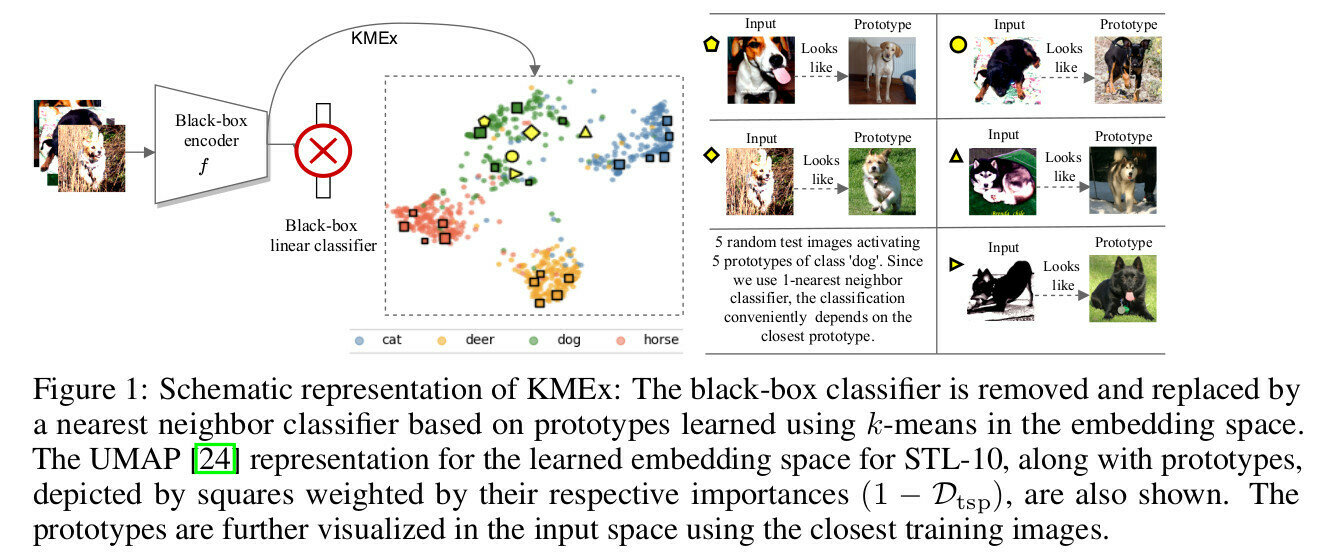
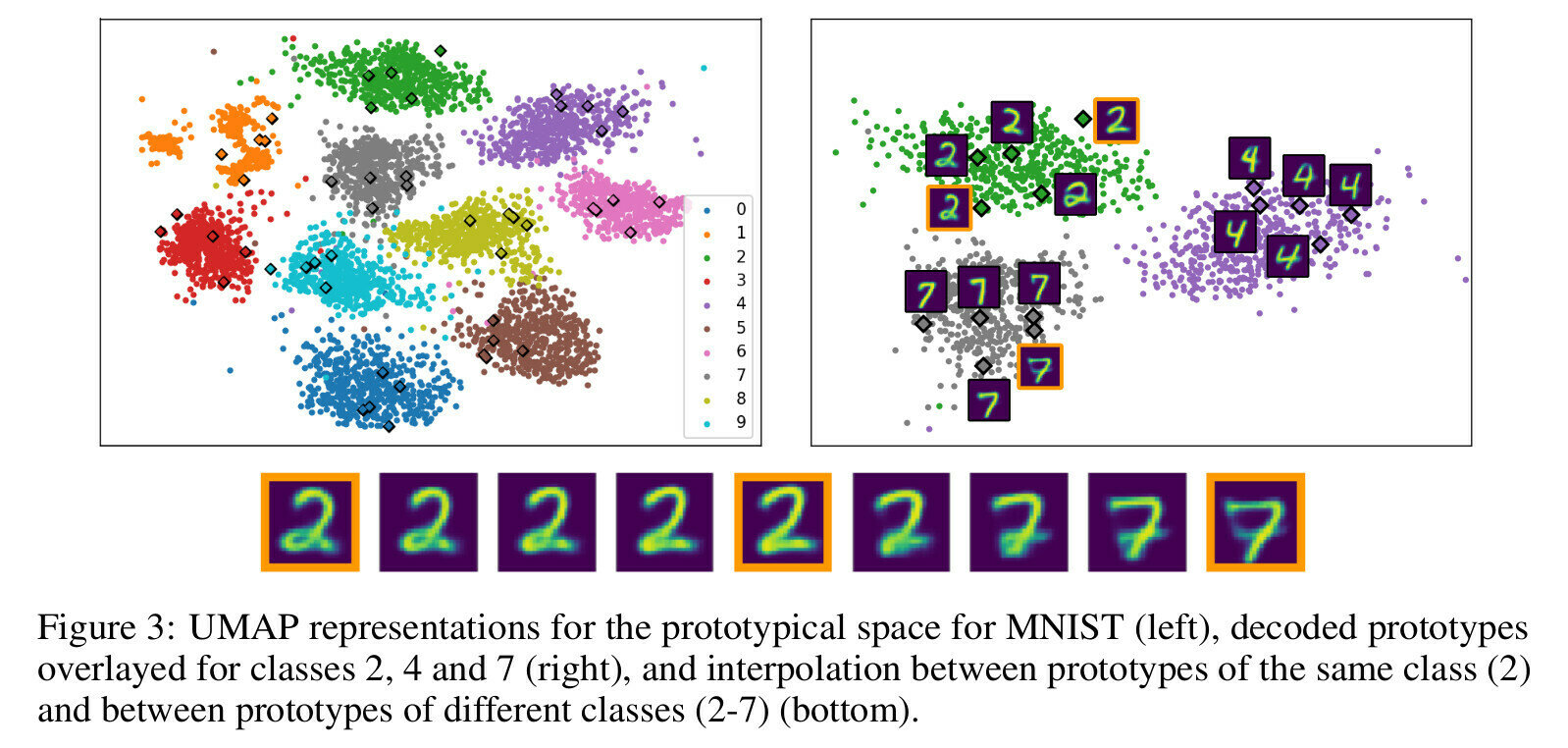
Local Explanation
- Concepts
- Prototypes
- Centroids
- ...
This looks like that
That because of this
- Heat-map
- Saliency
- Attribution
- ...
Local Explanation
Definitions & Properties
Transparency
The relationship between prototypes, embedding and predictions is interpretable.
Trustworthiness
Faithful if its classification accuracy and explanations match its black-box counterpart.
Robust local and global explanations.
Diversity
Non overlapping information between prototypes.
Three Predicates
Definitions & Properties
What is Diversity?
Geometric diversity
In the embedding
Combinatorial diversity
In terms of attributes
High Geometric
Low Combinatorial
Low Geometric
High Combinatorial
High Geometric
High Combinatorial
Celis, L. Elisa, et al. "How to be fair and diverse?." arXiv:1610.07183 (2016)
Self-Explainable Models
Self-Explainable Models
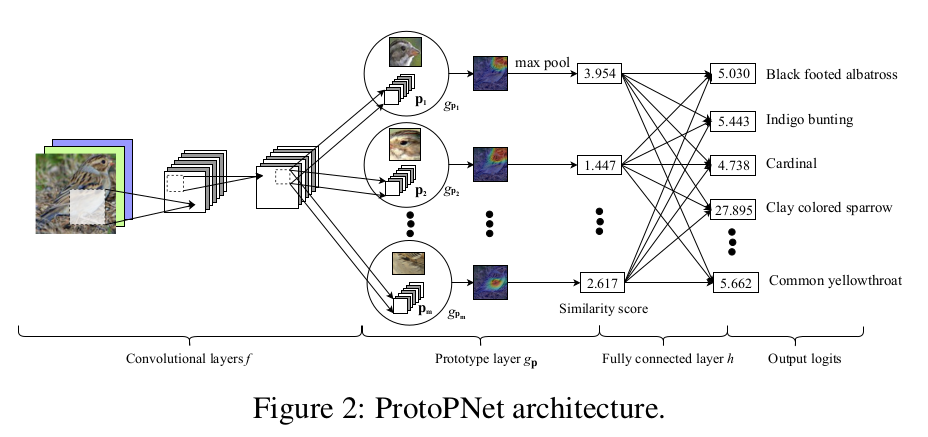
ProtoPNet
Chen, Chaofan, et al. "This looks like that: deep learning for interpretable image recognition." Neurips, 2019.
Loss Function
\mathcal{L} = \mathbf{CE}( h \circ g_p \circ f(x), y ) + \mathcal{L}_\mathrm{Clst}(z,p_y) + \mathcal{L}_\mathrm{Sep}(z,p_{\neg y})
Difficult to train
Brings x closer to
class prototypes
Pushes x away from
other classes' prototypes
Alternating optimization:
GD and Prototypes
Conv.
Pool.
z
s
\phi
Prototypes
y
Self-Explainable Models
FLINT
Parekh, Jayneel, Pavlo Mozharovskyi, and Florence d'Alché-Buc. "A framework to learn with interpretation." Neurips, 2021.
Loss Function
\mathcal{L} = \mathbf{CE}( f(x), y ) + \mathbf{CE}(g(x),f(x)) + \mathcal{L}_\mathrm{cd}(\Psi(x)) + \mathcal{L}_\mathrm{if}(d \circ \Psi,x)
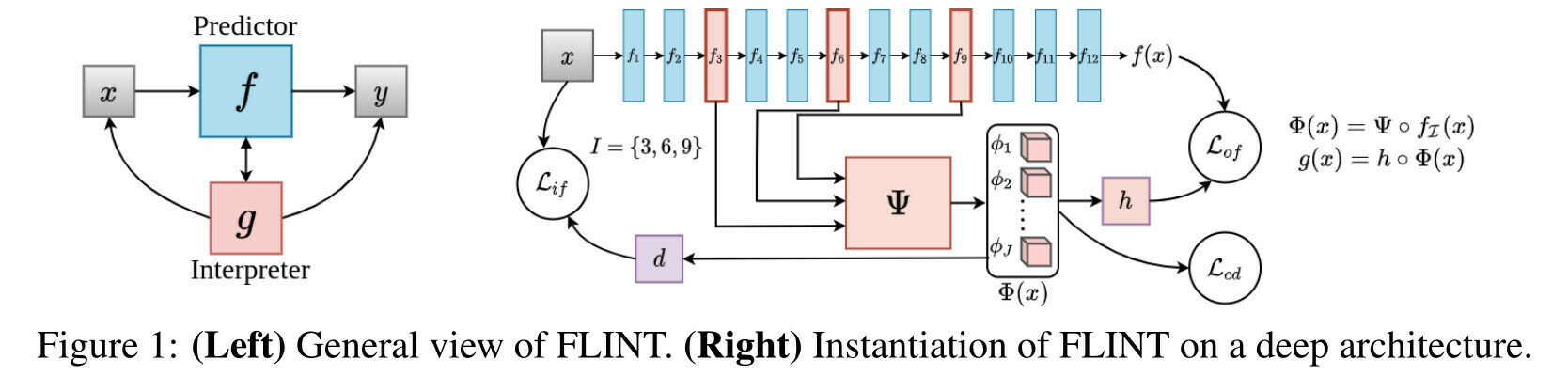
Difficult to train
Regularize the usage
of the prototypes
"Improve the quality"
of the feature activations
Alternating optimization:
Not all losses all the time
Conv.
Pool.
z
s
\phi
Prototypes
y
Self-Explainable Models
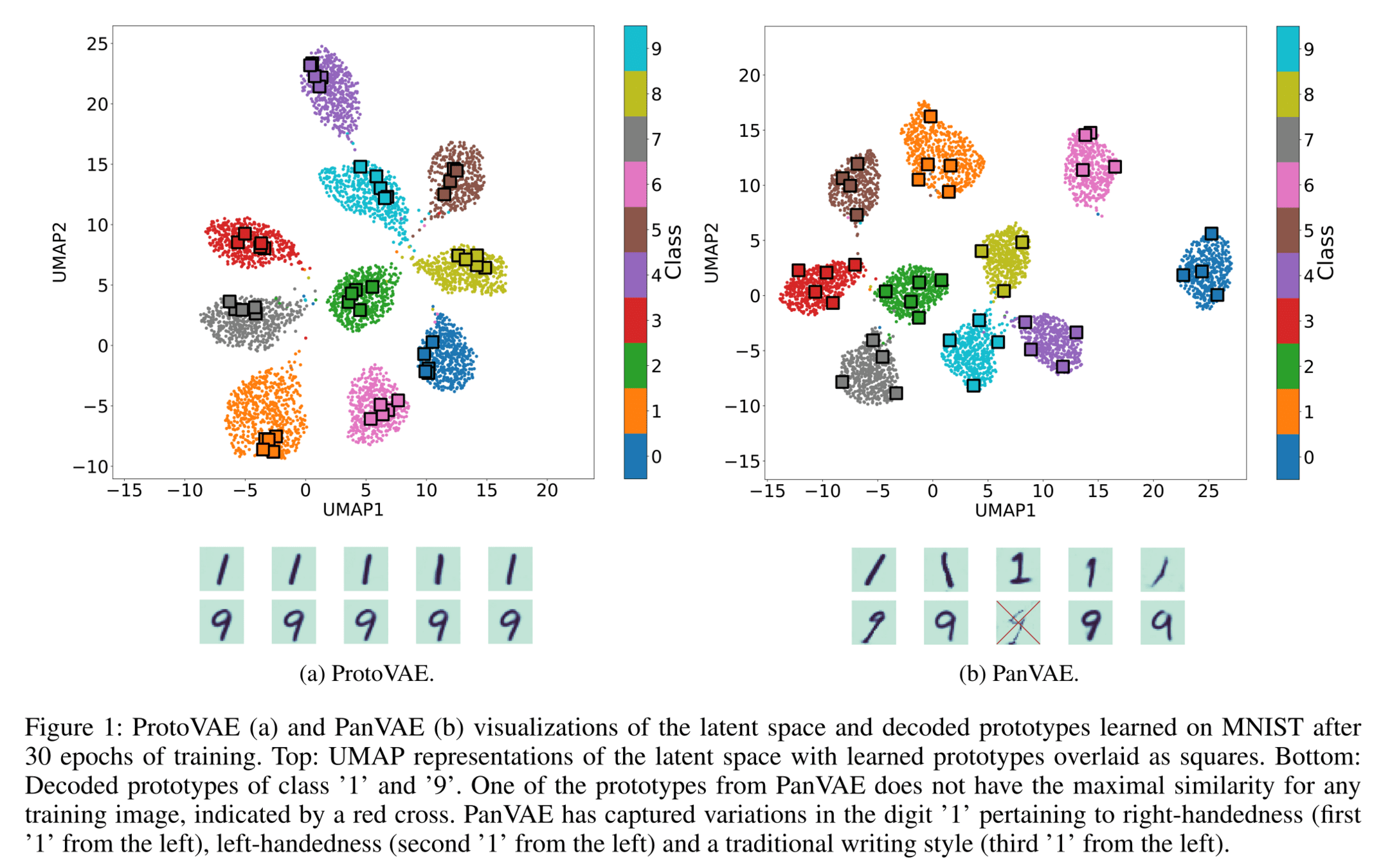
Self-Explainable Models
Pantypes
Kjærsgaard, Rune, Ahcène Boubekki, and Line Clemmensen. "Pantypes: Diverse representatives for self-explainable models." AAAI, 2024.
Loss Function
\mathcal{L}_{\mathrm{Pantypes}}=\mathcal{L}_{\mathrm{pred}} + \mathcal{L}_{\mathrm{VAE}} + \frac{1}{K} \sum_{k} \frac{1}{|\mathbf{G}_k|^\frac{1}{2}}
Conv.
Pool.
z
s
\phi
Prototypes
y
Self-Explainable Models
Pantypes loss function:
\mathcal{L}_{\mathrm{Pantypes}}=\mathcal{L}_{\mathrm{pred}} + \mathcal{L}_{\mathrm{VAE}} + \frac{1}{K} \sum_{k} \frac{1}{|\mathbf{G}_k|^\frac{1}{2}}
\text{with} \: \mathbf{G}_k = \mathbf{\Phi}^T_k \mathbf{\Phi}_k
Maximize the volume
of the prototypical Gram matrix.
⇝ Maximize norm and rank of .
\mathbf{\Phi}_k
IF USED!
Regularized by the VAE loss
Maximize the volume
of the prototypical Gram matrix.
⇒ Maximize norm and rank of .
\mathbf{G}_k
"Unused" prototypes diverge out-of-distribution
maximizes the norm and rank of the prototypes
\mathcal{L}_\mathrm{vol}
regularizes the norm of "used" prototypes
\mathcal{L}_\mathrm{VAE}
\mathcal{L}_{\mathrm{Pantypes}}=\mathcal{L}_{\mathrm{pred}} + \mathcal{L}_{\mathrm{VAE}} + \mathcal{L}_{\mathrm{vol}}
Self-Explainable Models
Norm constraint
too strong
Missing
OOD prototype
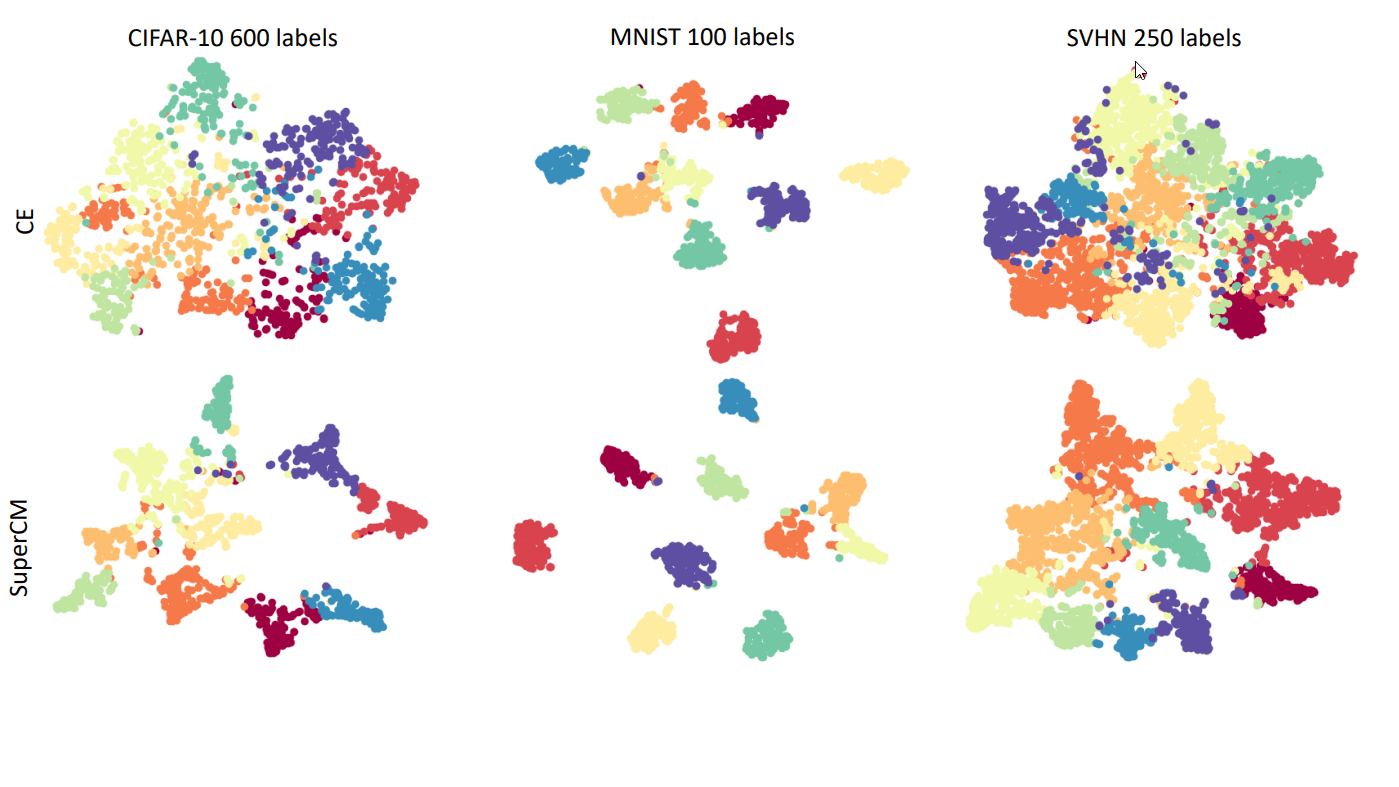
Evaluation
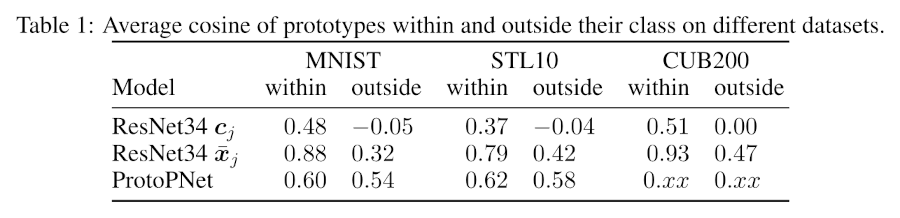
Quantitative
Evaluation
Baseline
z
y
y
s
\phi
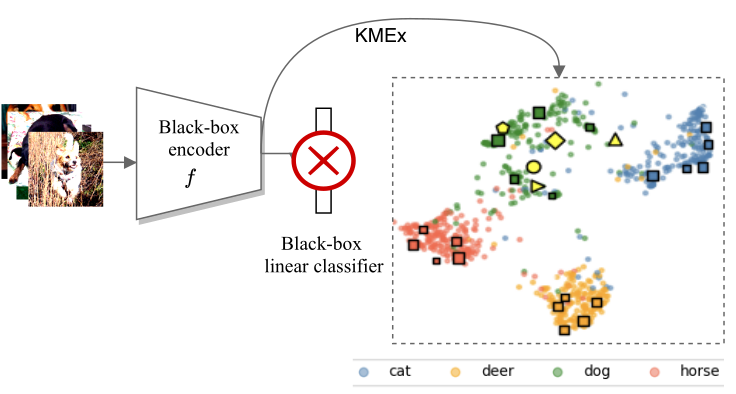
Prototypes
Simil.
Transparent
Classifier
y
Such prototypes are not good
How to learn the prototypes with minimum impact?
k-means
Transparent Classifier?
Nearest neighbor
Dist.
1NN Clf.
Prototypes/Centroids
Frozen
KMeX
Definitions & Properties
Transparency
The relationship between prototypes, embedding and predictions is interpretable.
Trustworthiness
Faithful if its classification accuracy and explanations match its black-box counterpart.
Robust local and global explanations.
Diversity
Non overlapping information between prototypes.
Three Predicates
Evaluation
The relationship between prototypes, embedding and predictions is interpretable.
Transparency
Some prototypes are never used
Breach
Evaluation
Performs on par with black-box models while providing robust explanations.
Trustworthiness
Evaluate the difference between the explanations
Missing
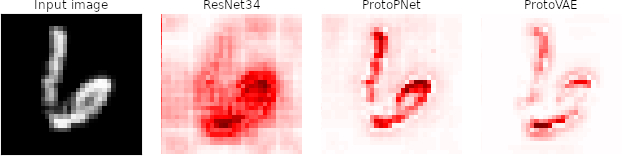
Evaluation
Non overlapping information between prototypes.
Diversity
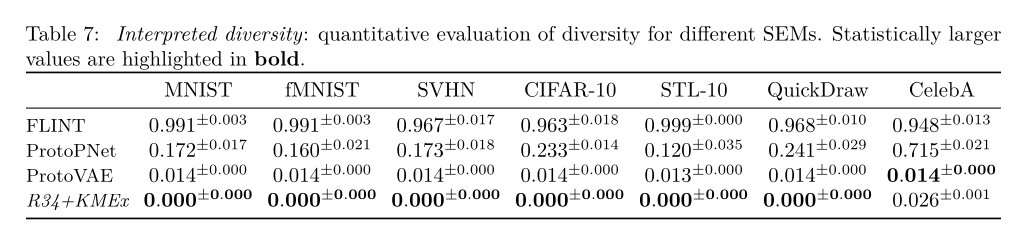
Missing
Quantitative Evaluation
with respect to the similarity measure
Distance and dot-product-based similarity yield different embeddings.
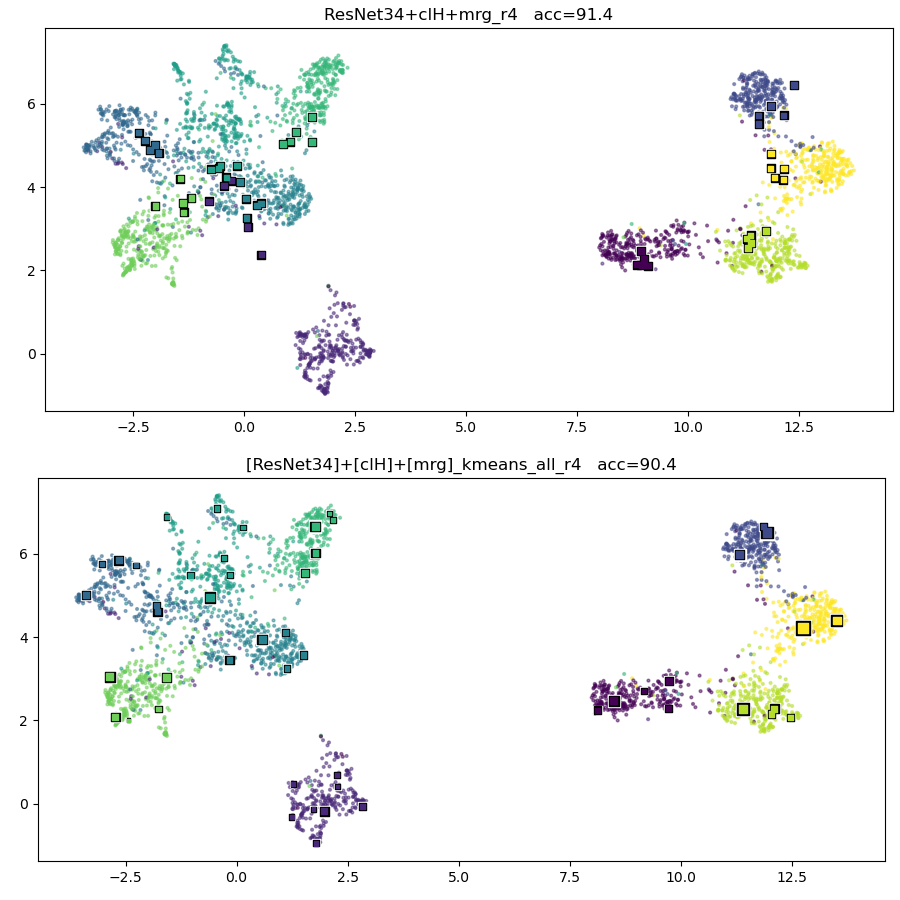
dot-product simil.
distance simil.
Evaluation
Summary
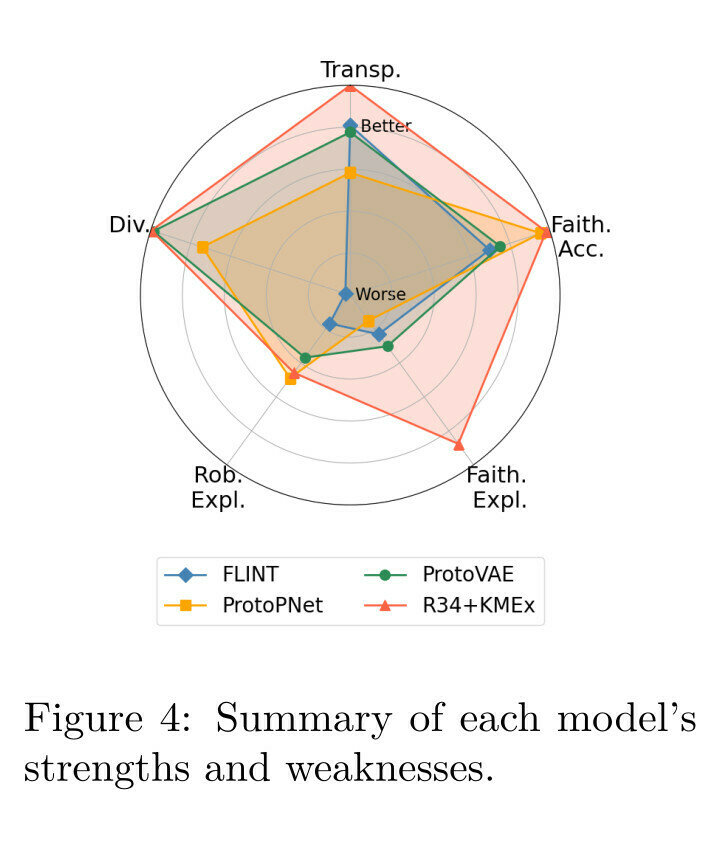
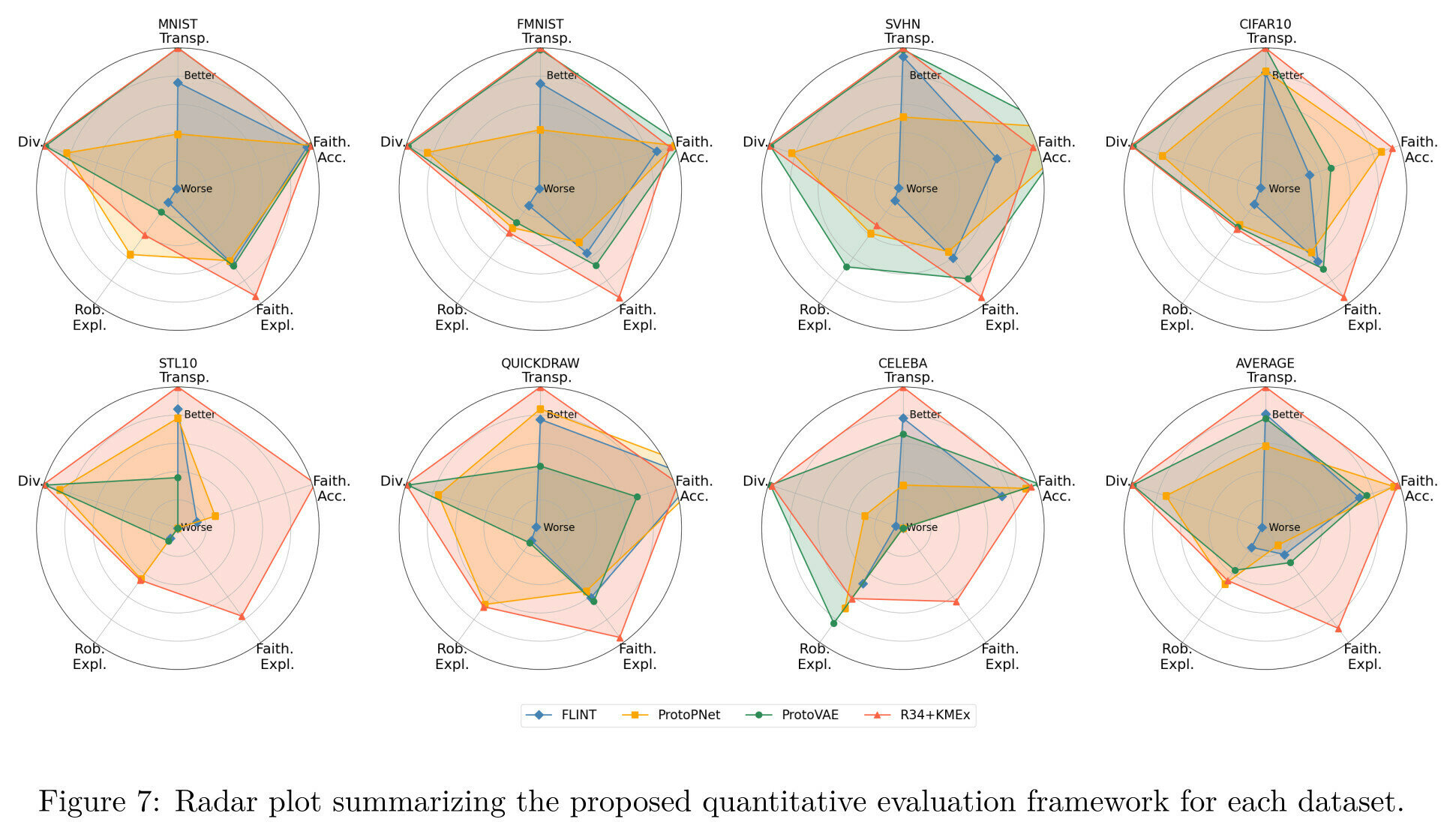
Summary
Summary
Evaluation
- A training-free baseline: KMeX.
- Pay attention to ghosting/fidelity/diversity
- No need to be best at everything!
Architectures
- A CNN is an SEM
- Consistent architectures
- Training is difficult
- Diversity is the most difficult requirement
Summary
Conv.
Pool.
z
s
\phi
Prototypes
y
Conv.
Pool.
z
s
\phi
Prototypes
y
Conv.
Pool.
z
s
\phi
Prototypes
y
ProtoVAE, Pantypes, KMeX
ProtoPNet, KMeX
FLINT ... KMeX?
Future Work
Future Work
Extending KMeX to Feature Activations
Dataset:
DeepGlobe Land Cover.
803 images of size 2448×2448.
80300 patches of size 224×224.
7 labels (type of land).
Model:
ResNet34 trained for multi-label predictions.
Explanations:
Outputs of blocks 2, 3 and 4.
k-means with 20 clusters.
Future Work
Extending KMeX to Feature Activations
Ahcène Boubekki
Prototypes and
Self-Explainable Models
UCPH/Pioneer
Self Explainable Models
By ahcene
