DECISION TREES ASSIGNMENT

September 20, 2016

CODE

TASK 1

Exploring the Dataset

EXCEL / CALC / NUMBERS

use filters and functions

USE A SCRIPTING LANGUAGE

PYTHON

RUBY

JS

OPEN CSV IN RUBY

 require 'csv'

 csv = File.read('/path/to/titanic.csv')

 dataset = CSV.parse(csv, :headers => true)
 puts dataset.count # => 891

FILTERING RECORDS

died = dataset.select { |e| e['survived'] == '0' }.count
# => 549

survived = dataset.select { |e| e['survived'] == '1' }.count 
# => 342

ENTROPY

AND

GINI

ENTROPY

  def entropy(probablities)
    probablities.reduce(0.0) do |sum,p|       if p > 0
        sum += p * Math.log2(p)      else        sum += 0      end
    end * -1
  end

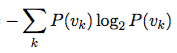
GINI

  def gini(probablities)
    probablities.reduce(0.0) do |sum,p| 
      sum += p * (1 - p)
    end
  end

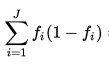
PURITY

 def purity(mixtures, &block)
   purity = mixtures.reduce(0.0) do |sum,m|
     size = m.reduce(:+).to_f
     measure = yield(m.collect { |n| n/size })
     sum += size > 0 ? size * measure : 0
   end
   purity / mixtures.flatten.reduce(:+)
 end

ENTROPY & GINI OF DATASET

  died     = dataset.select { |e| e['survived'] == '0' }.count
  survived = dataset.select { |e| e['survived'] == '1' }.count

  dataset_entropy = purity([[died,survived]]) { |ps| entropy(ps) }
  dataset_gini    = purity([[died,survived]]) { |ps| gini(ps) }

  puts "Entropy of dataset = #{dataset_entropy}"
  puts "Gini of dataset    = #{dataset_gini}"

  # Entropy of dataset = 0.9607079018756469
  # Gini of dataset    = 0.4730129578614427

IG after pclass split using Entropy

IG after pclass split using Gini   

IG after embarked split using Entropy 

0.024047090707960517

IG after embarked split using Gini    

0.015751498294317823

TASK 2

BUILD SIMPLE 

DECISION TREE

IG(GENDER) 

> 

IG(PCLASS) 

> 

IG(EMBARKED)

ROOT NODE

SPLIT MALES BY

EMBARKED

AND

PCLASS

IG(MALE-PCLASS) 

>

IG(MALE-EMBARKED)

TREE

WE JUST NEED 2 LEVEL TREE

PLURALITY-VALUE

TREE

SPLIT FEMALES BY

EMBARKED

AND

PCLASS

FIND IG IN EACH CASE

IG(FEMALE-PCLASS) 

>

IG(FEMALE-EMBARKED)

TREE

USE PLURALITY-VALUE

PERFORMANCE

if the test example 

is a female then she will survive 

else if male he dies. 

For simplicity if we use our entire training set as the test set, 

predicted outcome will be 

577 will die 

and

314 will live

But from the data we know that actually only 

549 dies

342 survives

Number of incorrectly predicted 
109 male + 81 female = 190

Error percentage = 21%

Success percentage = 79%

WEKA

FIN.