Sistema de control sobre Robot Diferencial
Alejandro Daniel José Gómez Flórez
Estudiante de Ingeniería de Control

Objetivo
La finalidad es implementar un sistema de control, que permita controlar las trayectorias sobre un robot móvil, cuya tracción está dada por la diferencia de velocidades de dos ruedas.
Trabajo Previo
En el semestre 2014-02 se realizó un estudio sobre el modelado de robots diferenciales, en un Proyecto Academico Especial dirigido por la profesora Eliana Arango y realizado por las estudiantes Verónica Londoño y Maria Clara Salazar.
Trabajo Previo
Se destaca el uso del modelado del sistema mecánico a partir de las ecuaciones de Euler-Lagrange:
Energía cinética
Energía Potencial
Lagrangiano
Fuerzas externas
Trabajo Previo
Variables de estado:
Modificaciones Trabajo Previo
Modificaciones Trabajo Previo
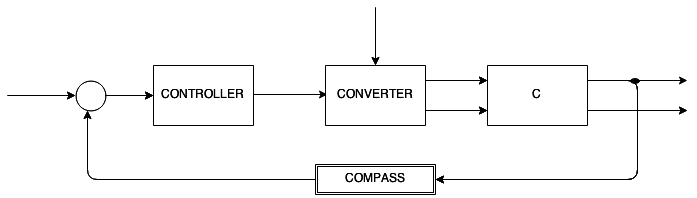
Modificaciones Trabajo Previo
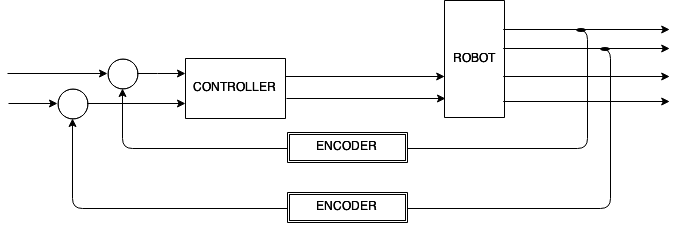
Modificaciones Trabajo Previo
la velocidad lineal y la velocidad angular de cuerpo del robot puede representarse como el promedio de la suma de las velocidades angulares
Modificaciones Trabajo Previo
La señal de salida:
Controlador:
Un polo más rápido para la solución de la ecuación de Diphantine.
Electrónica: Sensores
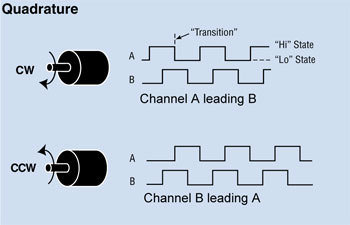
#define encoder0PinA 2
#define encoder0PinB 3
int encoder0Pos = 0;
unsigned int tmp_Pos = 1;
boolean A_set;
boolean B_set;
boolean flag = true;
void setup() {
pinMode(encoder0PinA, INPUT);
pinMode(encoder0PinB, INPUT);
pinMode(13, OUTPUT);
// encoder pin on interrupt 0 (pin 2)
attachInterrupt(0, doEncoderA, CHANGE);
// encoder pin on interrupt 1 (pin 3)
attachInterrupt(1, doEncoderB, CHANGE);
Serial.begin (9600);
}
void loop(){
digitalWrite(13, flag);
Serial.print("Index:"); Serial.print(encoder0Pos, DEC); Serial.println();
encoder0Pos = 0;
flag = !flag;
delay(100);
}
// Interrupt on A changing state
void doEncoderA(){
// Low to High transition?
if (digitalRead(encoder0PinA) == HIGH) {
A_set = true;
if (!B_set) {
encoder0Pos = encoder0Pos + 1;
}
}
// High-to-low transition?
if (digitalRead(encoder0PinA) == LOW) {
A_set = false;
}
}
// Interrupt on B changing state
void doEncoderB(){
// Low-to-high transition?
if (digitalRead(encoder0PinB) == HIGH) {
B_set = true;
if (!A_set) {
encoder0Pos = encoder0Pos - 1;
}
}
// High-to-low transition?
if (digitalRead(encoder0PinB) == LOW) {
B_set = false;
}
}
"The encoders provide a resolution of 1000 counts per three revolutions of the wheel."
Electrónica: Sensores
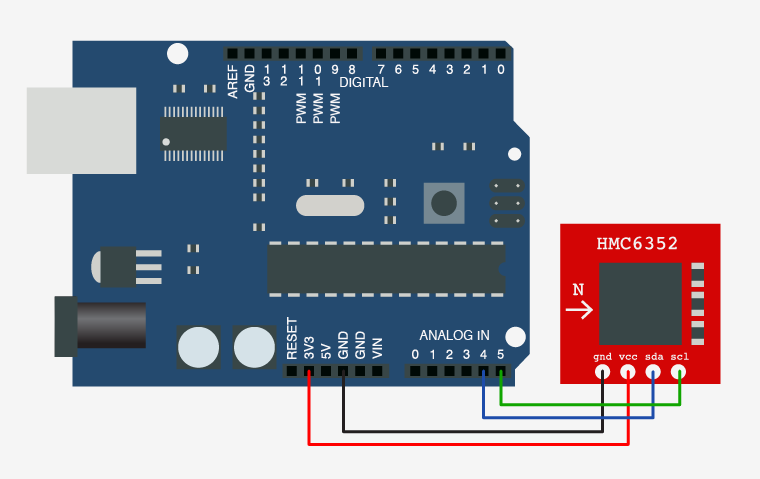
#include <Wire.h>
int compassAddress = 0x42 >> 1; // From datasheet compass address is 0x42
// shift the address 1 bit right, the Wire library only needs the 7
// most significant bits for the address
int reading = 0;
void setup()
{
Wire.begin(); // join i2c bus (address optional for master)
Serial.begin(9600); // start serial communication at 9600bps
}
void loop()
{
// step 1: instruct sensor to read echoes
Wire.beginTransmission(compassAddress); // transmit to device
// the address specified in the datasheet is 66 (0x42)
// but i2c adressing uses the high 7 bits so it's 33
Wire.write('A'); // command sensor to measure angle
Wire.endTransmission(); // stop transmitting
// step 2: wait for readings to happen
delay(10); // datasheet suggests at least 6000 microseconds
// step 3: request reading from sensor
Wire.requestFrom(compassAddress, 2); // request 2 bytes from slave device #33
// step 4: receive reading from sensor
if (2 <= Wire.available()) // if two bytes were received
{
reading = Wire.read(); // receive high byte (overwrites previous reading)
reading = reading << 8; // shift high byte to be high 8 bits
reading += Wire.read(); // receive low byte as lower 8 bits
reading /= 10;
Serial.println(reading); // print the reading
}
delay(100); // wait for half a second
}
Electrónica: Controlador



Electrónica: Encoders
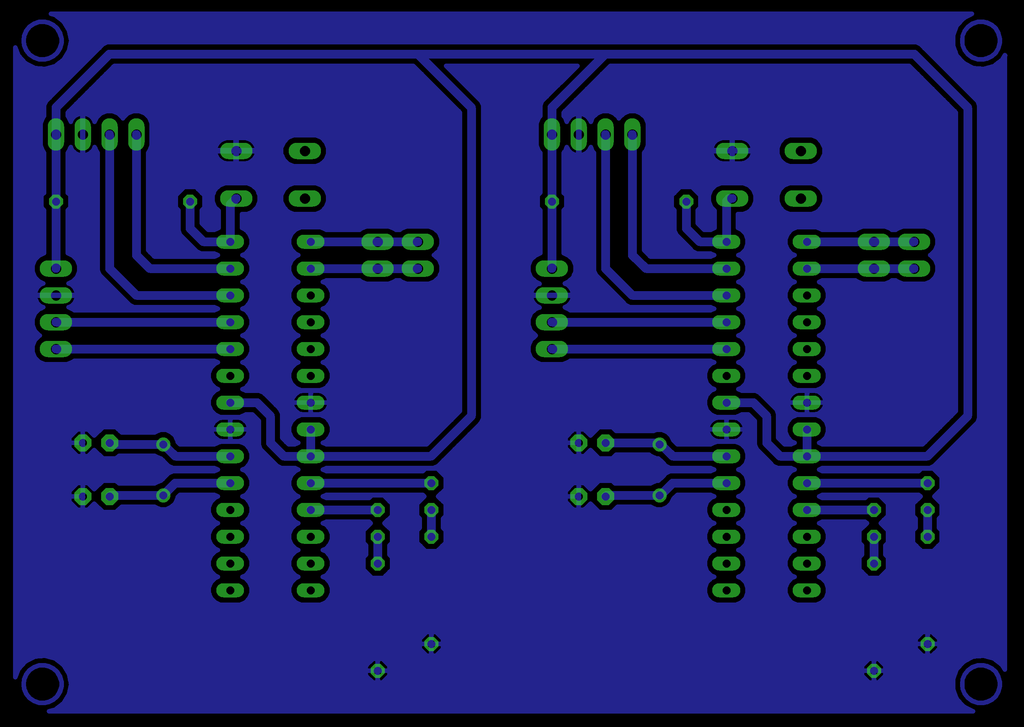


Uso de Encoders
By Alejandro Daniel Jose Gomez Florez
Uso de Encoders
- 928



