KD Tree

Outline

  • Introduction
  • Build
  • Insert
  • FindMin
  • Delete
  • K-Nearest
  • Query Range
  • Segment Tree

Introduction

KD-Tree = k-dimensional tree

一種在k維歐幾里德空間的資料結構

主要用於 範圍詢問 / 最鄰近詢問

Introduction

Build

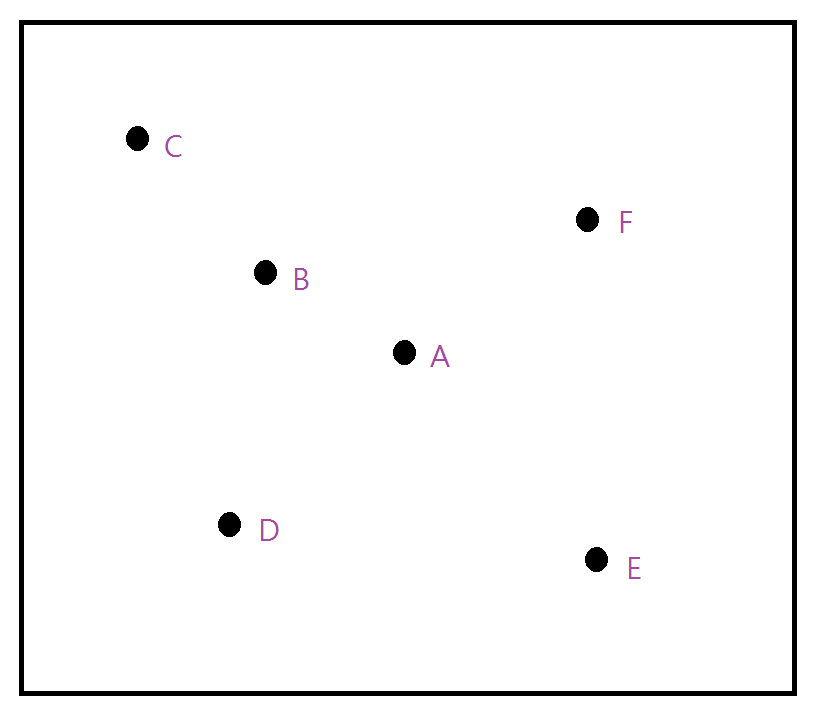
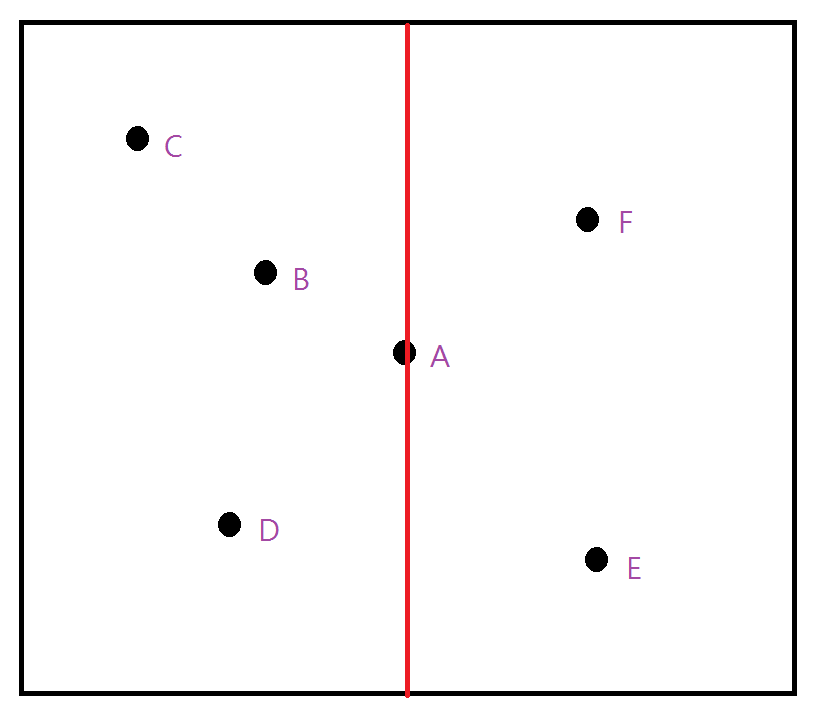
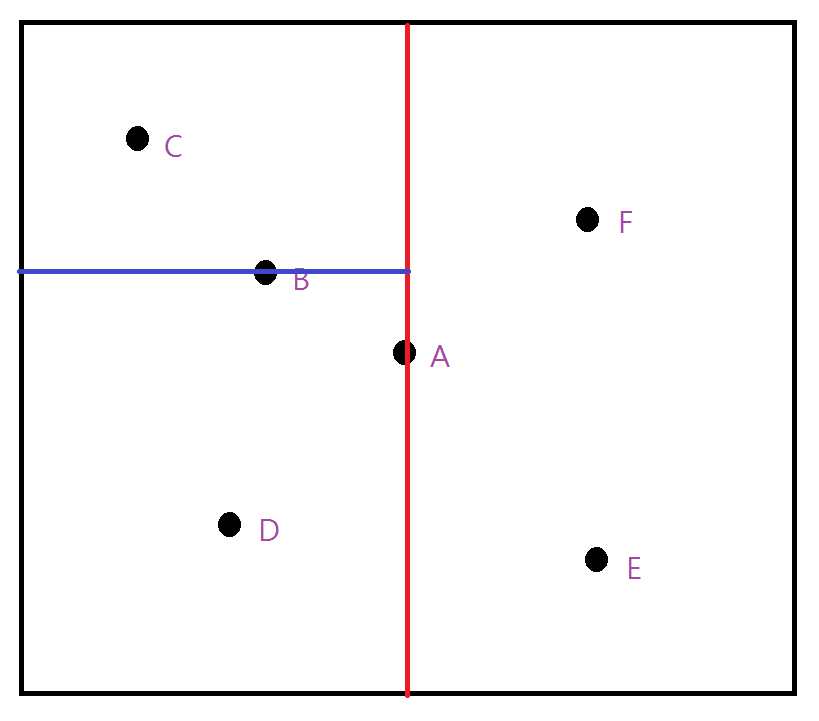
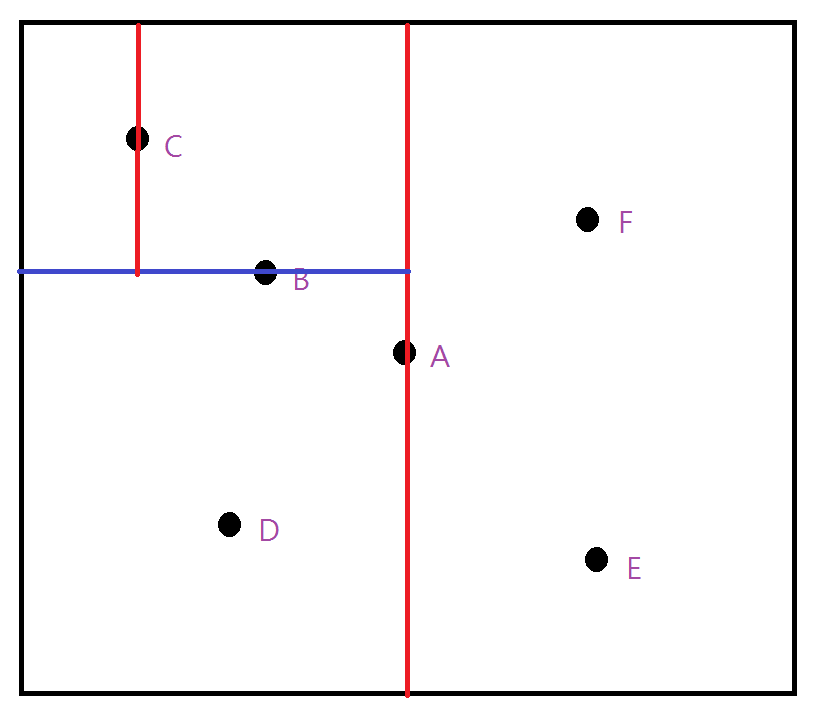
以二元樹儲存

將範圍內的點以不同的維度輪流切割

以中位數作為該子樹的樹根

Build

Build

Build

Build

Build

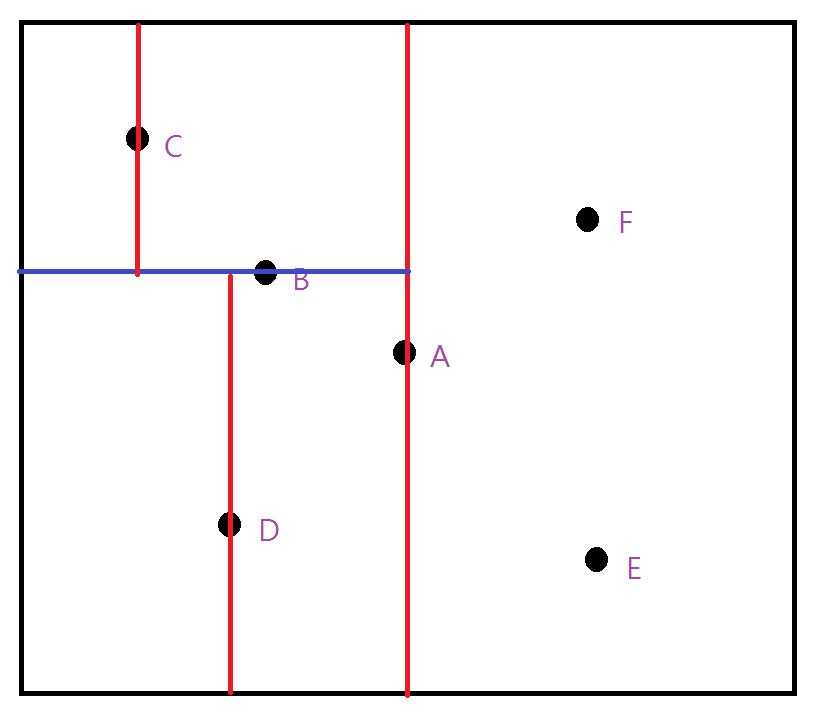
Build

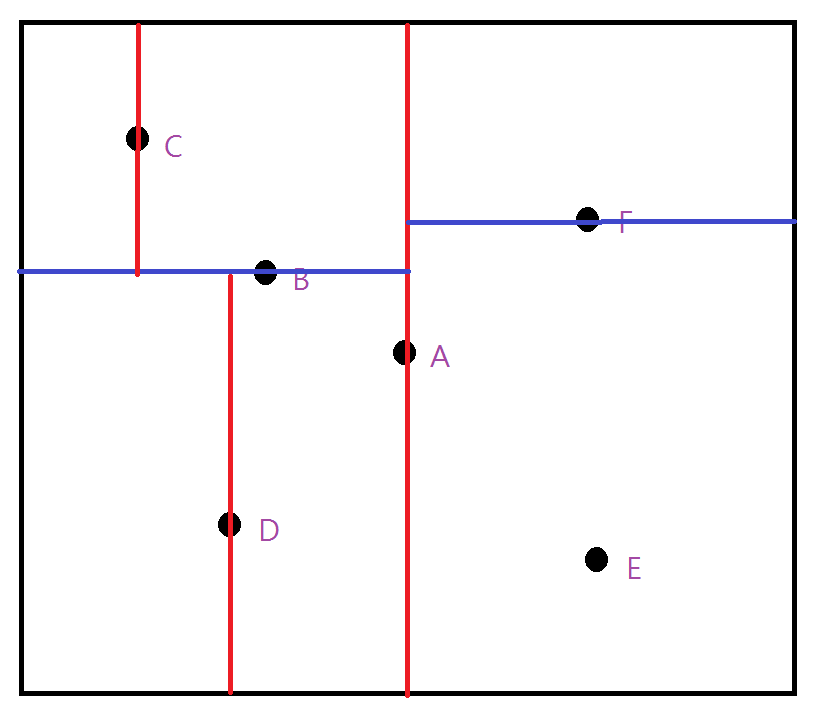
Build

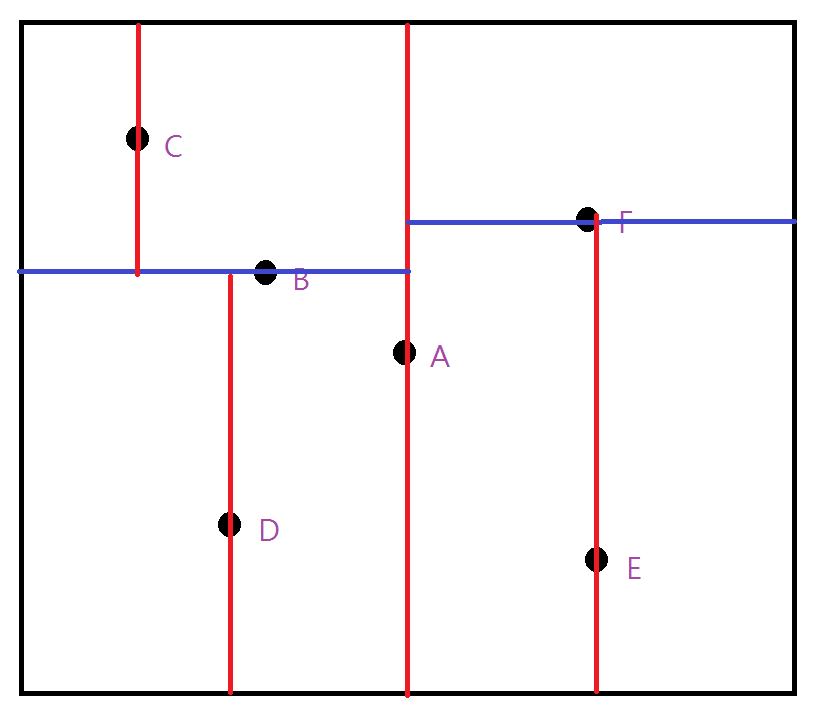
Build

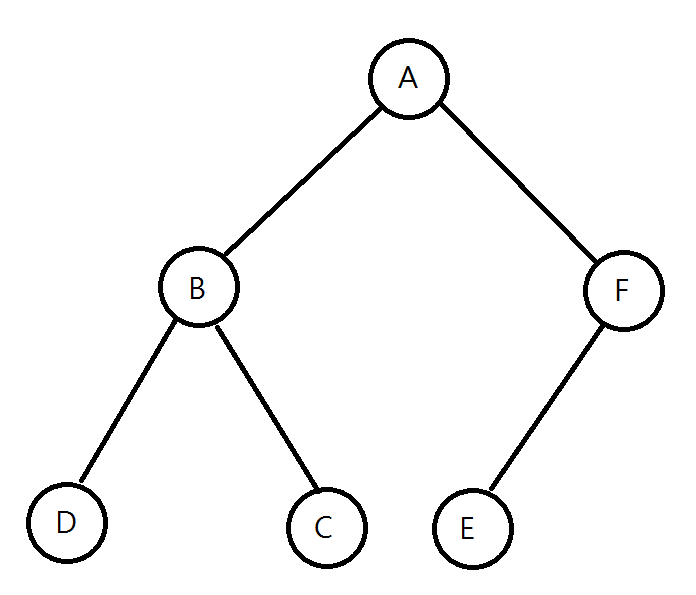
構造出的二元樹

Build

時間複雜度: O(NlogN)

找中位數: O(N) --- nth_element()

O(NlogN)
O(NlogN)O(NlogN)
O(N)
O(N)O(N)

   --- nth_element()

T(N) = 2 * T(\frac{N}{2}) + O(N) = O(NlogN)
T(N)=2∗T(N2)+O(N)=O(NlogN)T(N) = 2 * T(\frac{N}{2}) + O(N) = O(NlogN)

Insert

和一般二元樹的插入相同

依序用不同維度比較大小直到找到葉子

Insert

最壞複雜度: O(樹的高度)  = O(N)

二元樹的平衡可能會被破壞

經典解法: 替罪羊樹

均攤後複雜度: O(logN)

O(N)
O(N)O(N)
O(logN)
O(logN)O(logN)

FindMin

找到該子樹在第k維下的最小點

Delete的時候會用到

FindMin

如果該子樹是用目標維度分割

左子樹不為空 => 遞迴左子樹

左子樹為空 => 回傳該子樹的根

FindMin

如果該子樹不是用目標維度分割

分別往左右子樹遞迴取最小值

FindMin

複雜度分析

最多會經過 

複雜度: O(N1-1/k)

\alpha^{(k - 1) * \frac{log_{\alpha}{N}}{k}} = N^{1 - \frac{1}{k}}
α(k−1)∗logαNk=N1−1k\alpha^{(k - 1) * \frac{log_{\alpha}{N}}{k}} = N^{1 - \frac{1}{k}}
O(N^{1-\frac{1}{k}})
O(N1−1k)O(N^{1-\frac{1}{k}})

Delete

有兩種方法

第一種: 真的刪除

第二種: 標記刪除

Delete

真的刪除

找到要刪除的點後有三種情況

右子樹不為空 => Delete 右子樹的 Min Node

左子樹不為空 => Delete 左子樹的Min Node

並把剩下的左子樹變成右子樹

左右子樹都為空 => 直接砍掉該子樹

Delete

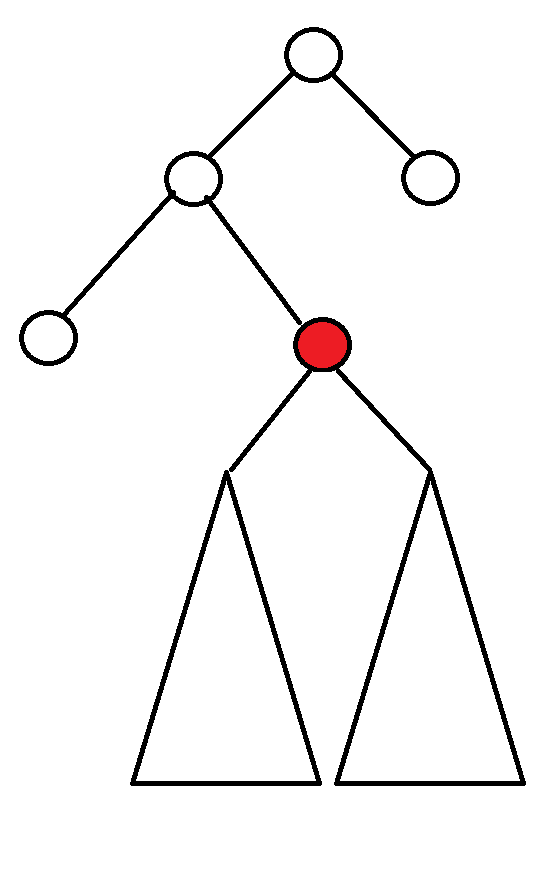
右子樹不為空

Delete

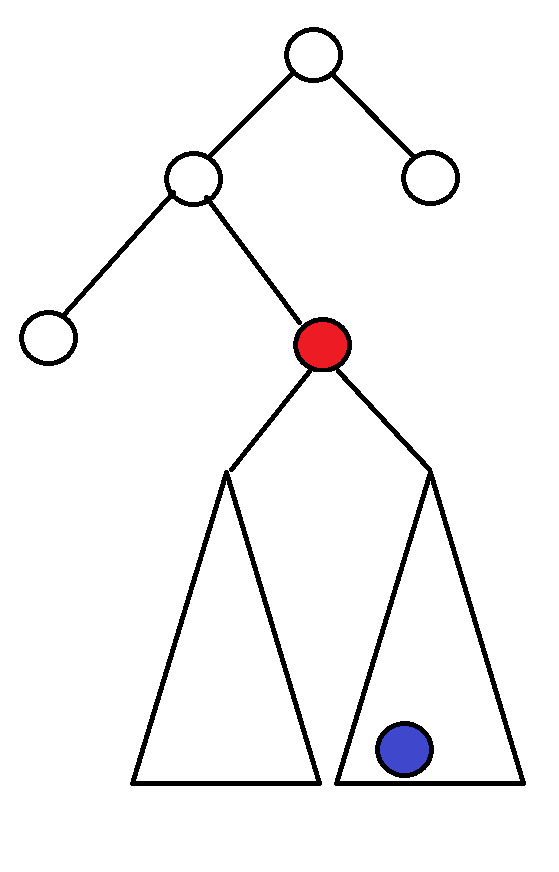
右子樹不為空

Delete

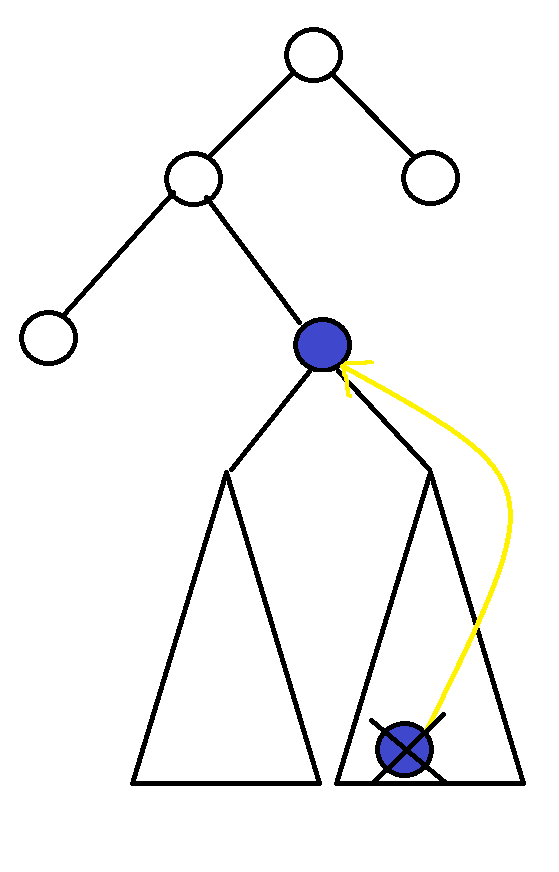
右子樹不為空

Delete

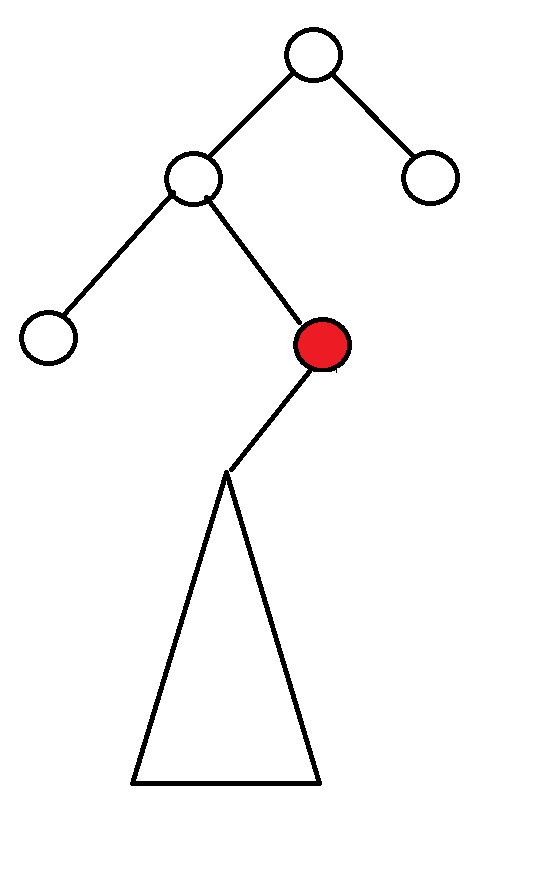
左子樹不為空

Delete

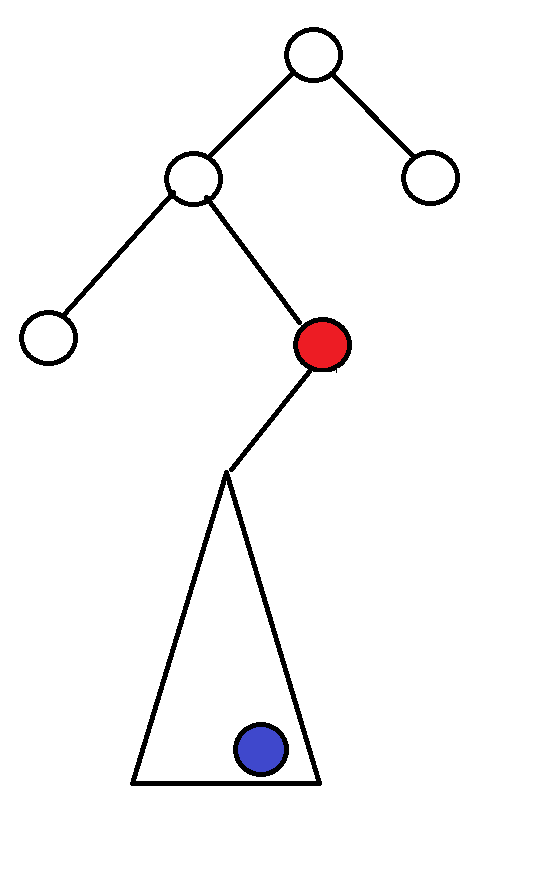
左子樹不為空

Delete

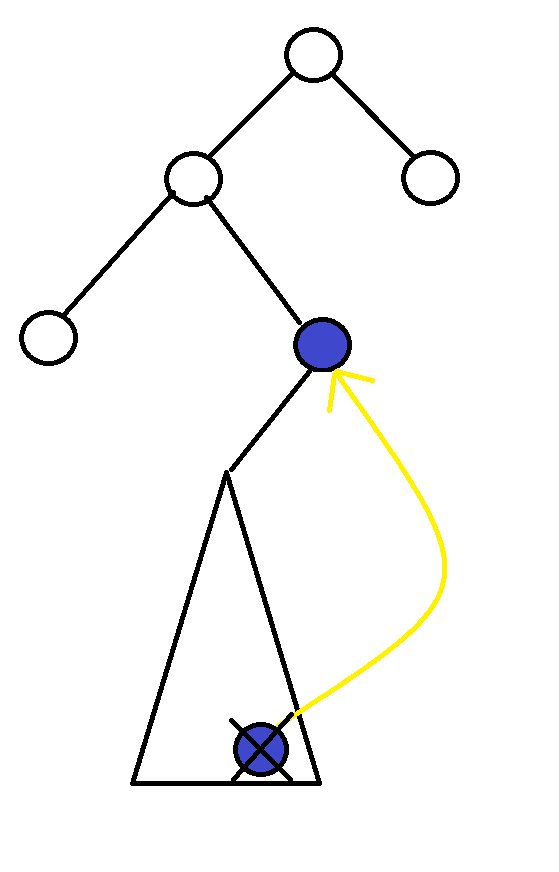
左子樹不為空

Delete

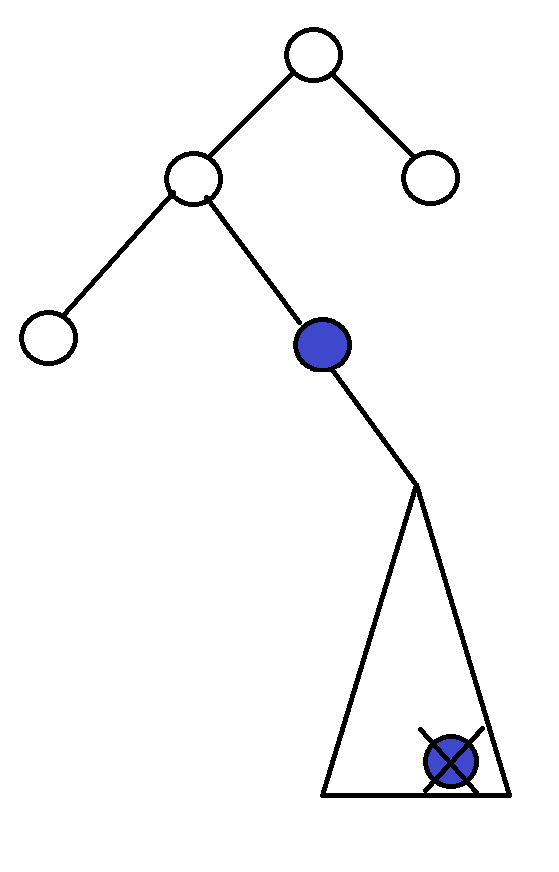
左子樹不為空

Delete

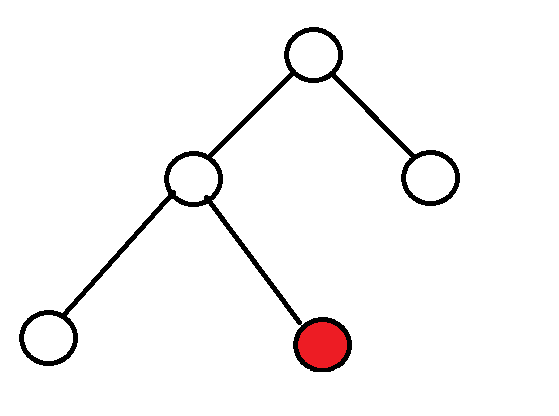
左右子樹都為空

Delete

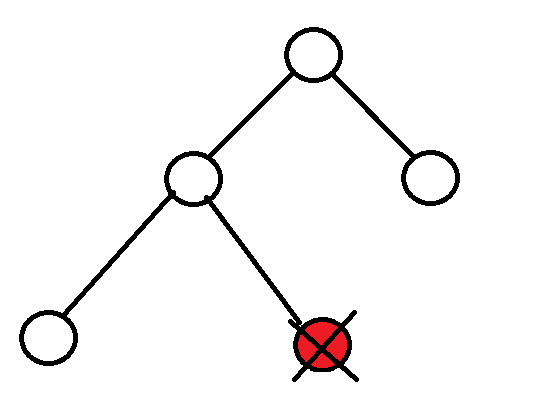
左右子樹都為空

Delete

複雜度分析

H = 樹的高度

O(FindMin + H)
O(FindMin+H)O(FindMin + H)

複雜度 = O(findmin + h)

=

O(N^{1-\frac{1}{k}}+H)
O(N1−1k+H)O(N^{1-\frac{1}{k}}+H)

Delete

標記刪除

找到要刪除的點後做標記

等重建的時候再把刪除的點拔掉

這方法在K-Nearest的時候會退化

但是有時候很方便

複雜度 = O(logN)

O(logN)
O(logN)O(logN)

K-Nearest

給定一個點 P

求距離 P 最近的 K 個點

K-Nearest

可以用 priority_queue 維護最近的 K 個點

比較 P 和該子樹的點，判斷左子樹和右子樹誰比較近

和 Insert 類似

K-Nearest

如果左子樹比較近

如果搜尋結果不足 K 個

先往左子樹遞迴搜尋

先把此子樹的點放進結果並往右子樹搜尋

否則將此子樹的點放入結果並把結果中最遠的拔掉

如果右子樹的點有可能比結果中的更好就往右子樹遞迴

K-Nearest

result = priority_queue

Search(node, P, K)
    if P is closer to left child:
        Search(node->left, P, K)
        if(size(result) < K):
            push node->point into result
            Search(node->right, P, K)
        else:
            if P is better than the farthest in result:
                push node->point into result
            if nodes in node->right may be better then point in result:
                Search(node->right, P, K)
    else:
        pass

K-Nearest

複雜度分析

最差複雜度還是 O(N^1-1/k)

平均複雜度 O(logN)

O(logN)
O(logN)O(logN)
O(N^{1-\frac{1}{k}})
O(N1−1k)O(N^{1-\frac{1}{k}})

Range Query

給定一個高維矩形

求矩形內的所有點

result = []
RangeQuery(node, L, R):
    if node->point in [L, R]:
        push node->point into result
    if range of node->left is included by [L, R]:
        RangeQuery(node->left, L, R)
    if range of node->right is included by [L, R]:
        RangeQuery(node->right, L, R)

Range Query

複雜度分析

P = 答案的數量

複雜度 = O(N^1-1/k + P)

O(N^{1-\frac{1}{k}}+P)
O(N1−1k+P)O(N^{1-\frac{1}{k}}+P)

Segment Tree

可以用高維 KD-Tree 模擬高維線段樹

Segment Tree

單點更新

Update(node, P, v):
    if node->point == P:
        update node->point with v
        return
    if P is in node->left:
        Update(node->left, P, v)
    else:
        Update(node->right, P, v)

Segment Tree

單點查詢

Query(node, P):
    if node->point == P:
        return data of node->point
    if P is in node->left:
        Query(node->left, P)
    else:
        Query(node->right, P)

Segment Tree

區間更新

Query(node, P):
    if node->point == P:
        return data of node->point
    if P is in node->left:
        Query(node->left, P)
    else:
        Query(node->right, P)
Update(node, L, R, v):
    if range of node in [L, R]:
        update lazy tag of node with v
        return
    if node->point in [L, R]:
        update data of node->point with v
    if range of node->left is included by [L, R]:
        Update(node->left, L, R, v)
    if range of node->right is included by [L, R]:
        Update(node->right, L, R, v)

Segment Tree

區間查詢

Query(node, L, R):
    if range of node in [L, R]:
        return data of node
    result = None
    if node->point in [L, R]:
        update result with data of node->point
    if range of node->left is included by [L, R]:
        update result with Query(node->left, L, R)
    if range of node->right is included by [L, R]:
        update result with Query(node->right, L, R)

KD Tree

By allenwhale

Made with Slides.com

KD Tree

  • 642

More from allenwhale