Drzewa Obszarów
Piotr Moczurad
Opis problemu
Mamy podany obszar w przestrzeni R^2 (jako [x_min, x_max] x [y_min, y_max]) oraz chmurę punktów. Interesują nas wszystkie punkty, które są zawarte w podanym obszarze.
Naiwny algorytm wyszukiwania działa w czasie liniowym względem ilości punktów (musimy wykonać dwa sprawdzenia dla każdego punktu).
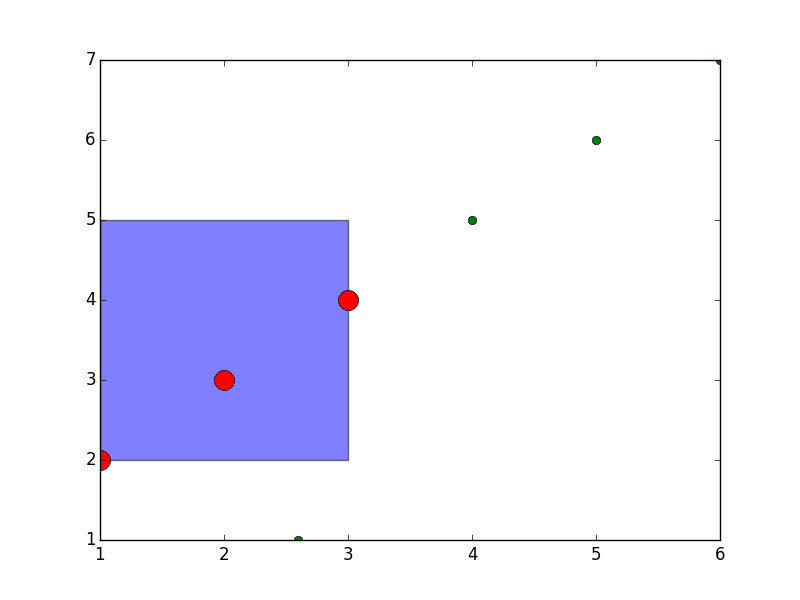
Drzewa obszarów -- pomysł
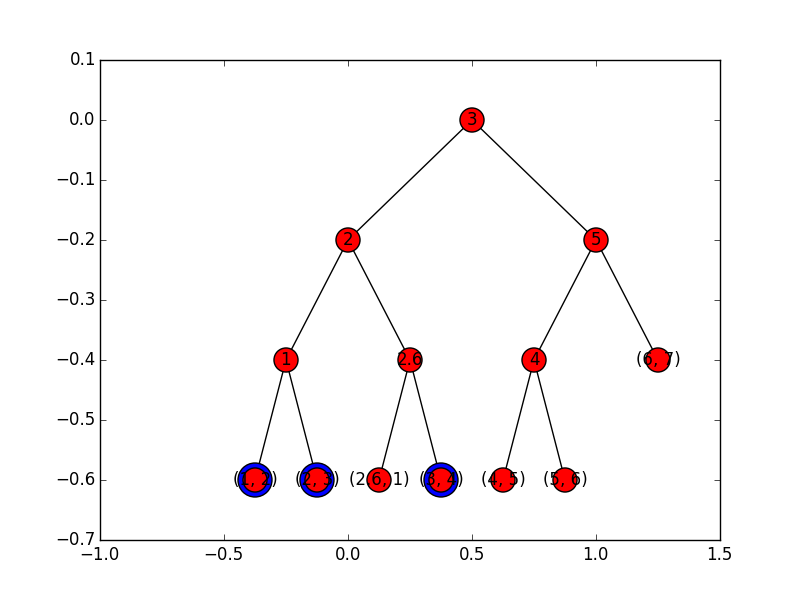
Tworzymy binarne drzewo wyszukiwań (BST), które w liściach trzyma nasze punkty.
Tworzone jest przez rekurencyjne podziały zbioru punktów na mniejsze lub równe medianie i większe od mediany (dzięki temu drzewo jest zawsze zrównoważone).
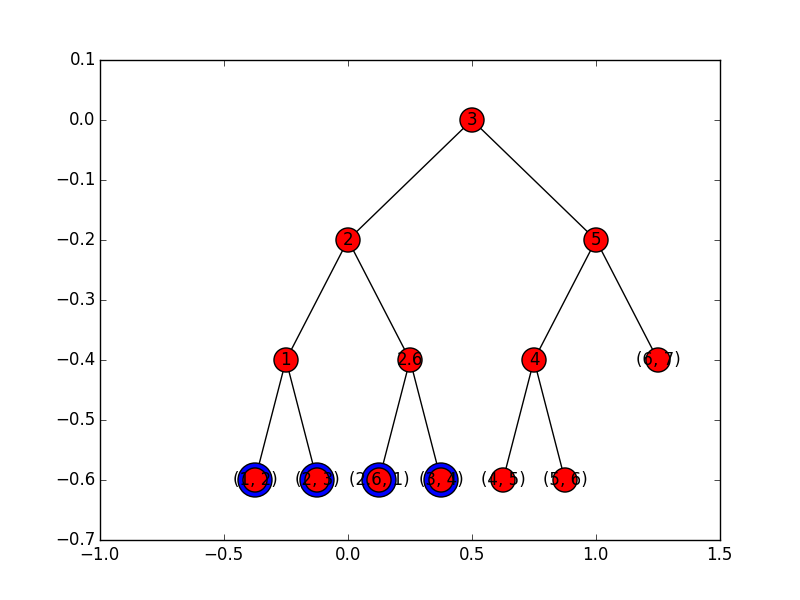
Drzewa obszarów -- pomysł cd
Wyszukiwanie opiera się na prostym pomyśle: dla dolnego końca przedziału (x_min) schodzimy ścieżką w drzewie do x_min, ale za każdym razem, gdy wykonujemy ruch do lewego poddrzewa, dołączamy do wyniku liście prawego poddrzewa. Jeśli dojdziemy do liści przy kroku w lewo, musimy sprawdzić, czy punkt mieści się w przedziale.
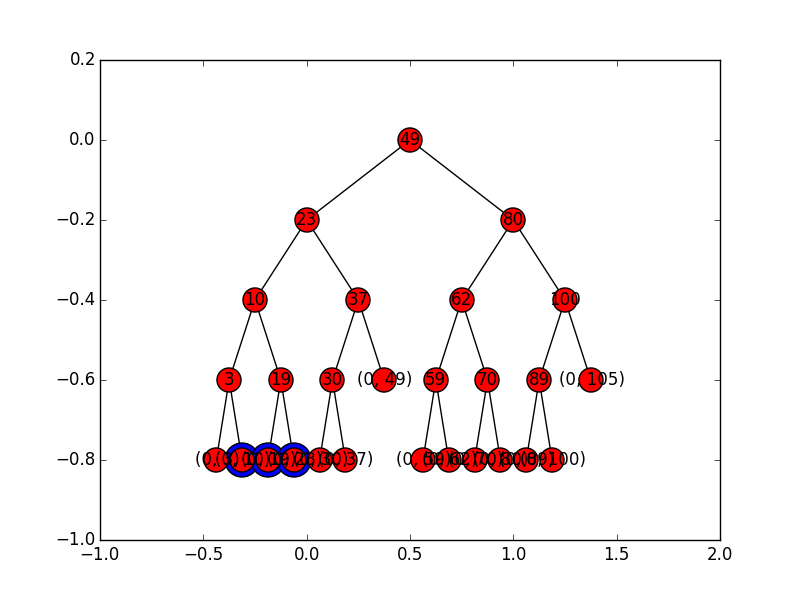
Drzewa obszarów -- 2D
Uogólnienie do dwóch wymiarów jest stosunkowo proste: drzewo wyszukiwań po pierwszej współrzędnej budujemy analogicznie, ale dla każdego węzła budujemy drzewo wyszukiwań po drugiej współrzędnej, ale tylko dla tych punktów, które znajdują się w poddrzewie obecnego węzła.
Drzewa obszarów -- 2D c.d.
Wyszukiwanie również przebiega podobnie:
jeśli znajdujemy się w liściu, to wystarczy sprawdzić, czy ma odpowiednie współrzędne;
w przeciwnym wypadku analogicznie do 1D schodzimy ścieżkami do x_min i x_max, ale zamiast dodawać liście poddrzew leżących "pod" ścieżką, wykonujemy zapytania w drzewie drugich współrzędnych.

Pseudokod (budowa)
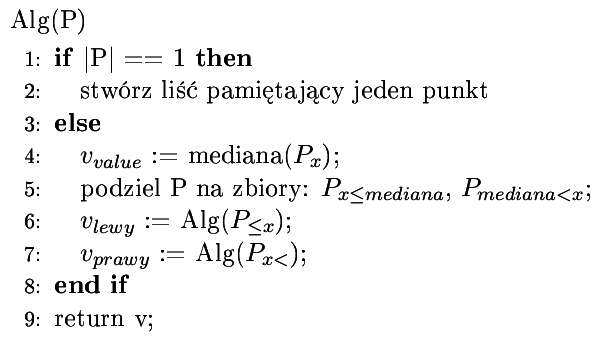
Pseudokod (przeszukiwanie)

Czasy działania
Naiwne przeszukiwanie działa liniowo względem każdej współrzędnej, a drzewa obszarów pozwalają nam ten czas zredukować do logarytmicznego względem ilości wierzchołków i liniowego względem liczby punktów w szukanym obszarze.
W związku z tym dla przestrzeni dwuwymiarowej naiwne przeszukiwanie potrzebuje O(n^2) kroków, a drzewa obszarów: O(log^2(n) + k).
Bibliografia
Zarówno algorytm jak i jego opis zostały napisane na podstawie jednej pracy. Jest ona również źródłem obrazków z pseudokodem.
https://www.ii.uni.wroc.pl/~prz/2010zima/zsd/zasoby/DrzewaObszarow.pdf
Drzewa Obszarów
By ambrozyk
Drzewa Obszarów
- 926



