Finding the ground state of spin Hamiltonians with reinforcement learning
Amin Mohamadi
Feb 5 2025
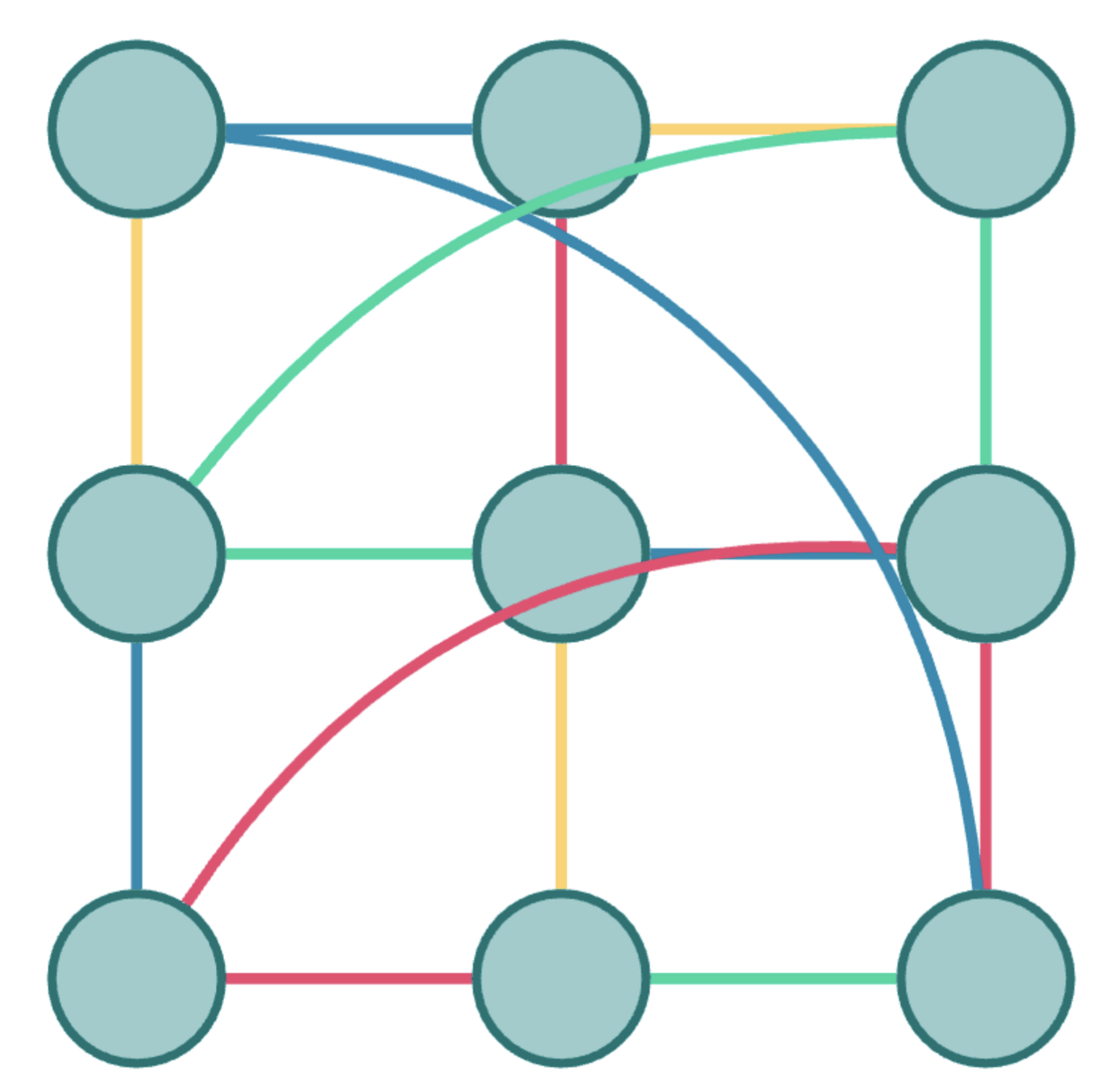
Spin Glass Problems
A graphical model, used for modelling a system as a set of binary spins, connected through interactions and exhibiting a certain bias for each spin.
- TSP
- Max-Cut
- Protein Folding
The Hamiltonian
- The Hamiltonian defines the energy of the system in a given state.
- The goal is to find global minima of the Hamiltonian, called Ground State. (NP-Hard due to non-convexity)
- Simulated Annealing (SA) is the go-to approach for finding ground state.
\mathcal{H} = - \sum_{i < j} J_{ij}\,\sigma_i\,\sigma_j \;-\; \sum_{i} h_i\,\sigma_i, \qquad \sigma_i = \pm 1, J_{ij} \in \mathbb{R}
Simulated Annealing
-
Inspired by metallurgy, where controlled heating and cooling help find a stable low-energy state.
-
An Optimization approach that mimics this process to solve NP-hard problems like spin glasses.
- At high temperatures, the system explores a wide range of states, avoiding local minima.
- As the temperature decreases, the system settles into an optimal (or near-optimal) solution.
Simulated Annealing
- Let \( s = s_0 \)
- For \( k = 0 \) through \( k_{\max} \) (exclusive):
- \( T \leftarrow \text{temperature} \left( 1 - \frac{k+1}{k_{\max}} \right) \)
- Pick a random neighbor, \( s_{\text{new}} \leftarrow \text{neighbour}(s) \)
- If \( P(E(s), E(s_{\text{new}}), T) \geq \text{random}(0,1) \):
- \( s \leftarrow s_{\text{new}} \)
- Output: the final state \( s \)
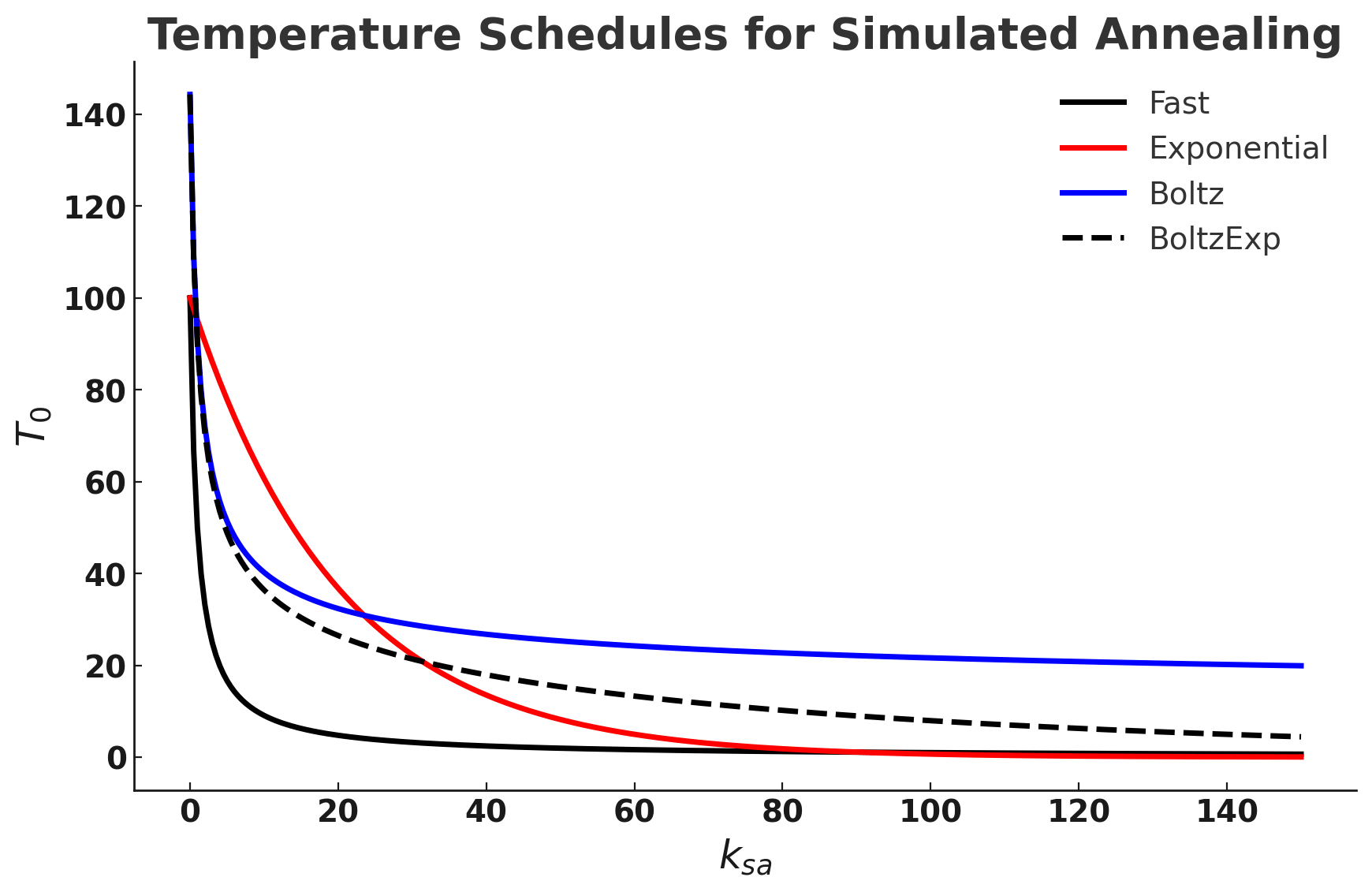
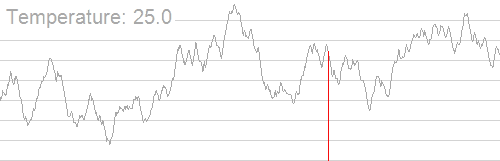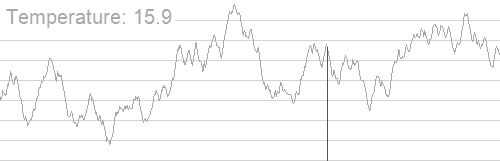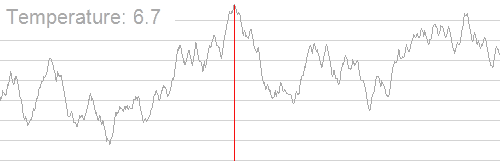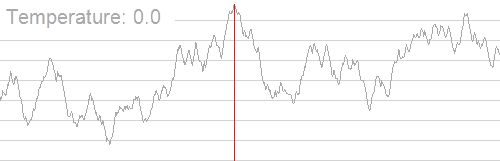
The Problem
- The success of Simulated Annealing is completely dependent on the temperature schedule.
- Temperature schedules are mostly based on heuristics:
- No adaptation according to specific instances.
- Requires manual tuning for different Hamiltonians.
- Scaling to higher problem complexities is cumbersome.
The Solution: RL
- Reinforcement Learning (RL) is a proven method for optimizing a procedure with a well-defined success measure.
- Deep reinforcement learning is now used to train agents with superhuman performance that play video games, board games, conduct protein folding and chip design.
- Main Idea: Use RL to control the temperature schedule of simulated annealing.
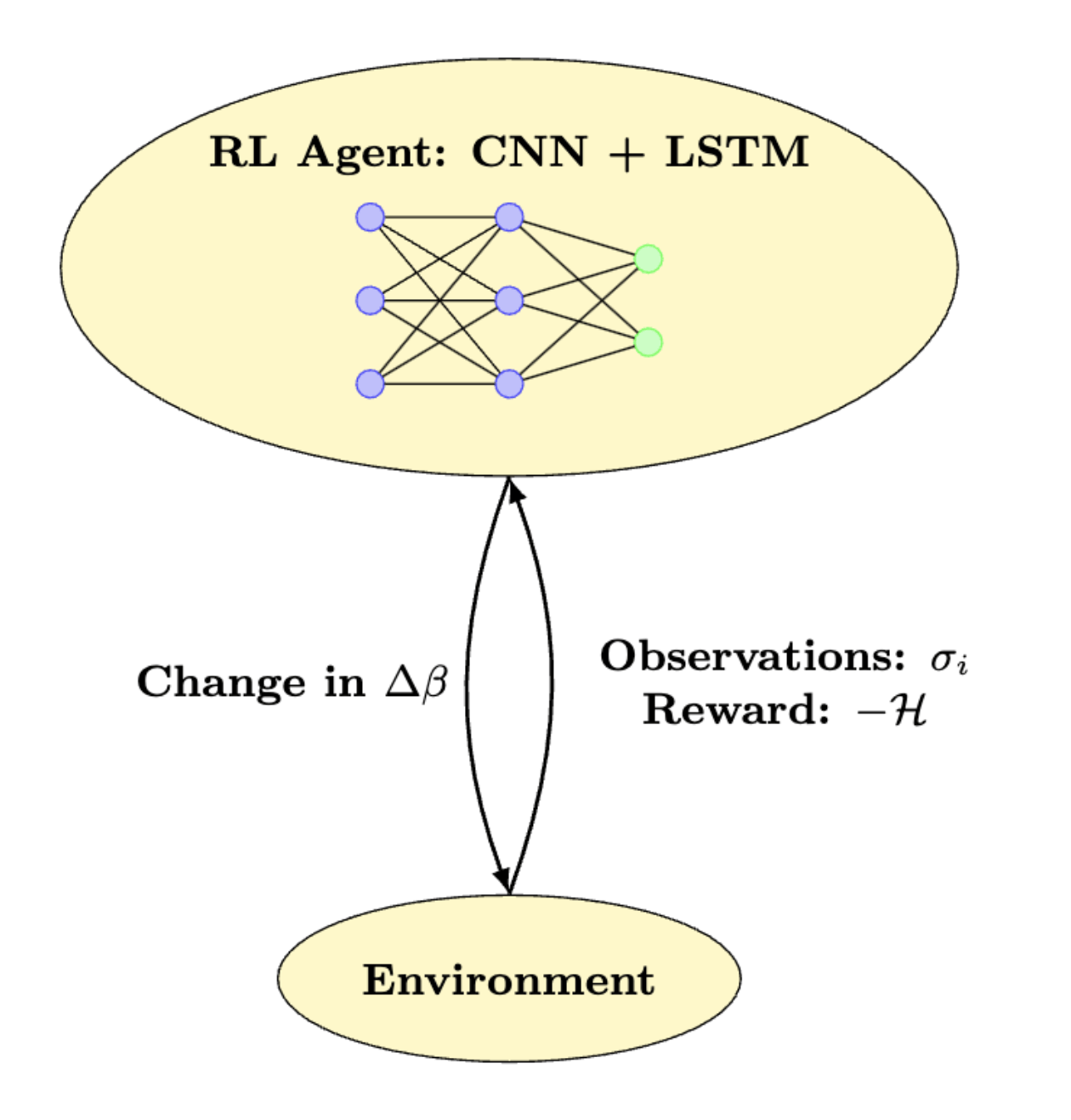
RL for Simulated Annealing
-
An RL agent receives an input state \(s_t\) at time \(t\), and decides to take action \(a_t\) based on a learnt policy function \(\pi_\theta(a_t \vert s_t)\) parameterized by \(\theta\) to obtain a reward \(R_t\).
- In Deep RL, policy function is represented by a neural network.
- In controlling Simulated Annealing, the agent observes the spins \(\sigma_i\) at time \(t\) and decides to change the inverse temperature by \(\Delta \beta\) to obtain a reward proportionate to negative of the energy of the system.
- An RL agent receives an input state \(s_t\) at time \(t\), and decides to take action \(a_t\) based on a learnt policy function \(\pi_\theta(a_t \vert s_t)\) parameterized by \(\theta\) to obtain a reward \(R_t\).
- In Deep RL, policy function is represented by a neural network.
RL for SA
-
State:
- \(N_{reps}\) replicas of randomly initialized spin glasses with \(L\) binary spins.
-
Action:
- A change in inverse temperature, sampled from \(\mathcal{N}(\mu, \sigma^2)\), where \(\mu, \sigma^2\) are outputs of agent.
-
Reward:
- Negative of minimum energy achieved across replicas.

RL Optimization Process
-
The agent (neural network) is optimized using a well-known RL algorithm: Proximal Policy Optimization (PPO).
- \(L^{CLIP}\) represents the policy loss: how likely is the network to take actions that maximize the reward?
- \(L^{VF}\) represents the value estimation: how well can the agent estimate the future rewards?
- \(S[\pi_\theta]\) represents the entropy of the outcomes: how diverse are the actions that agent takes?
L^{\text{PPO}} (\theta) = \hat{\mathbb{E}}_t \left[ L^{\text{CLIP}} (\theta) - c_1 L^{\text{VF}} (\theta) + c_2 S[\pi_{\theta}](s_t) \right]


Experimental Results:
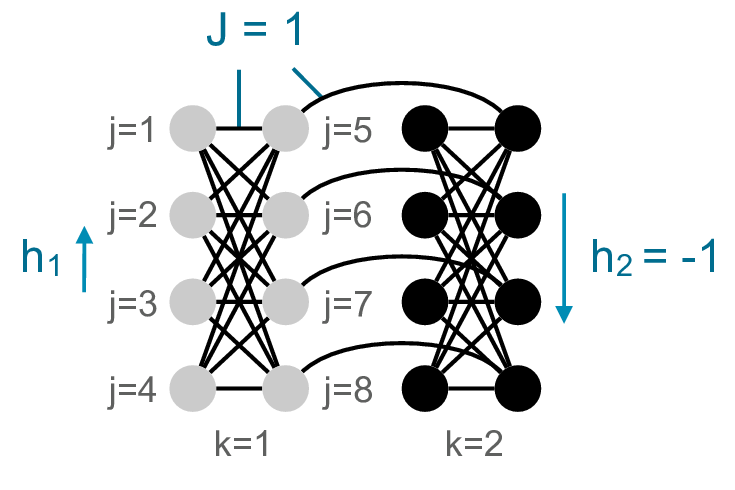
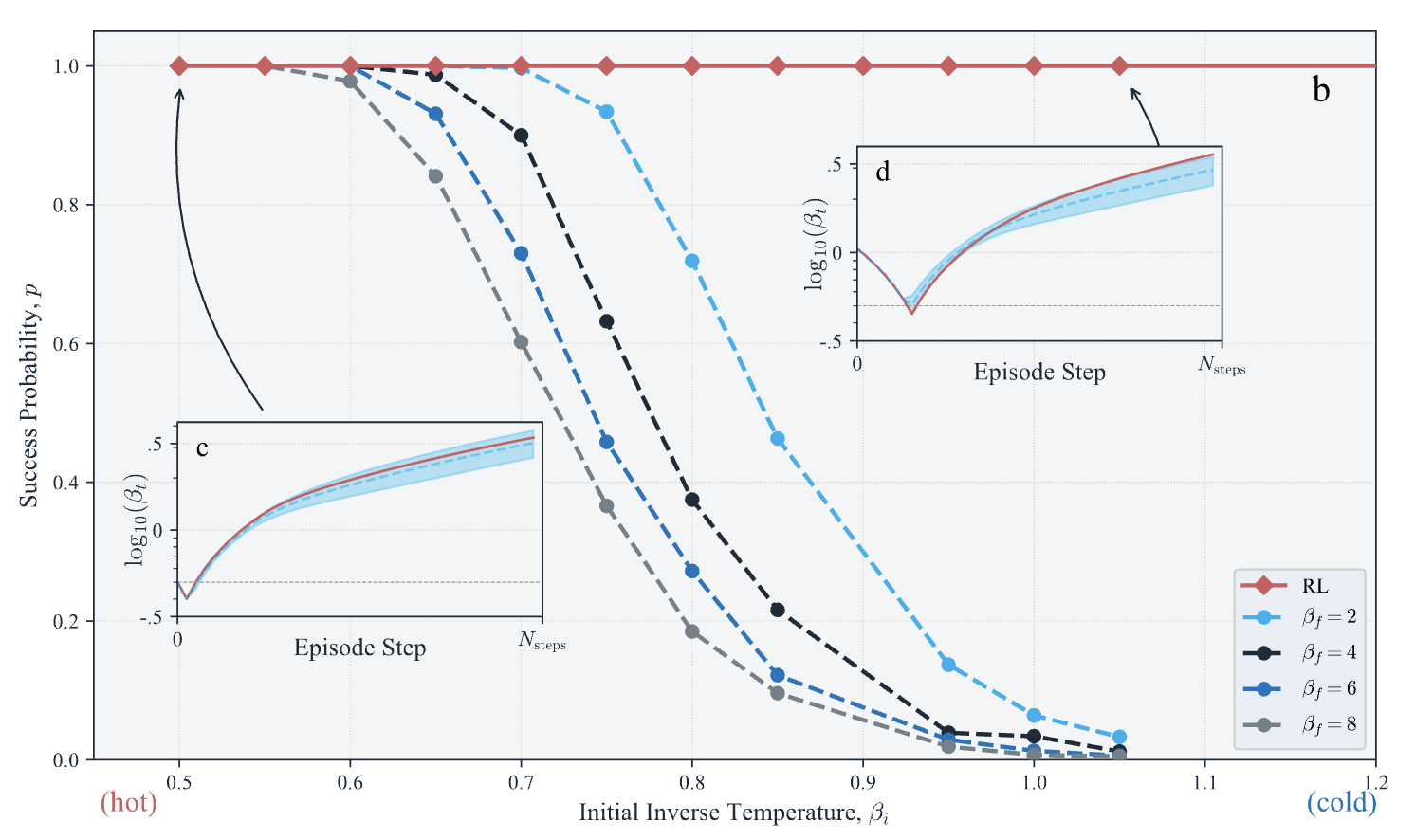
Weak-Strong Clusters
-
Weak-Strong Clusters (WSC) are a specific class of spin-glasses known for having a severe local minima next to their global minima.
- In evaluation, all WSC
instances were initialized
in a local minima.
- The initial temperature
can be cool or hot.
Experimental Results:
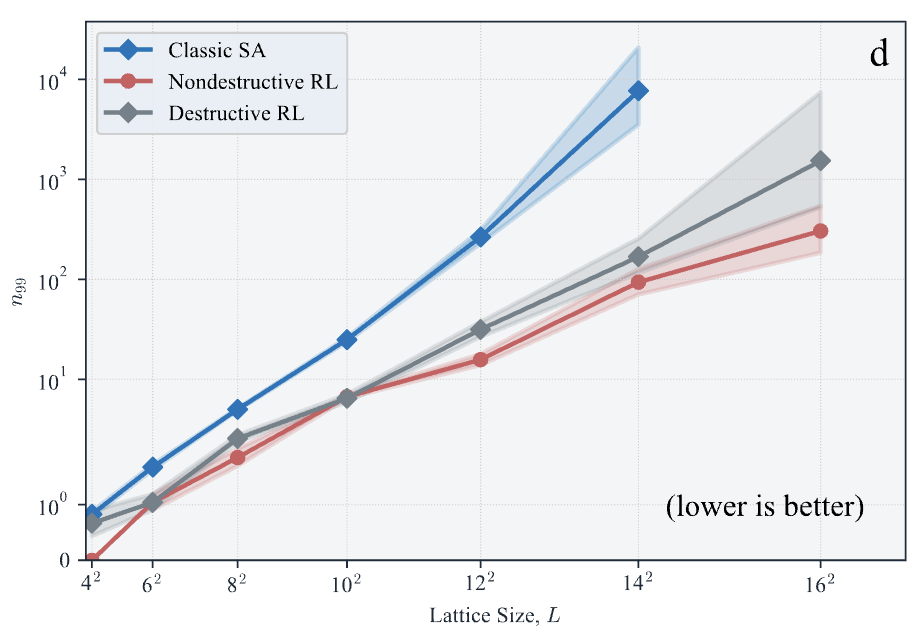
Spin Glass
-
The agent has also been tested on general spin-glass problems without specific structures.
- Apart from specific instances,
the scaling capability of the
proposed algorithm was also
investigated.
- Surprisingly, RL scales better
than classical SA schedules.

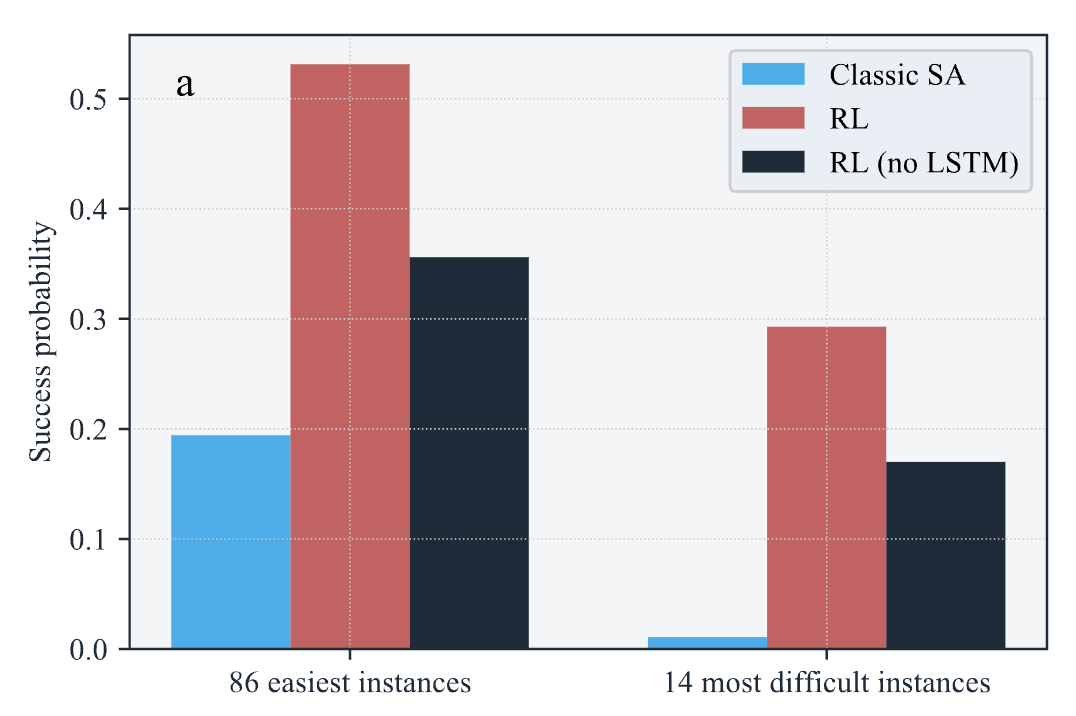
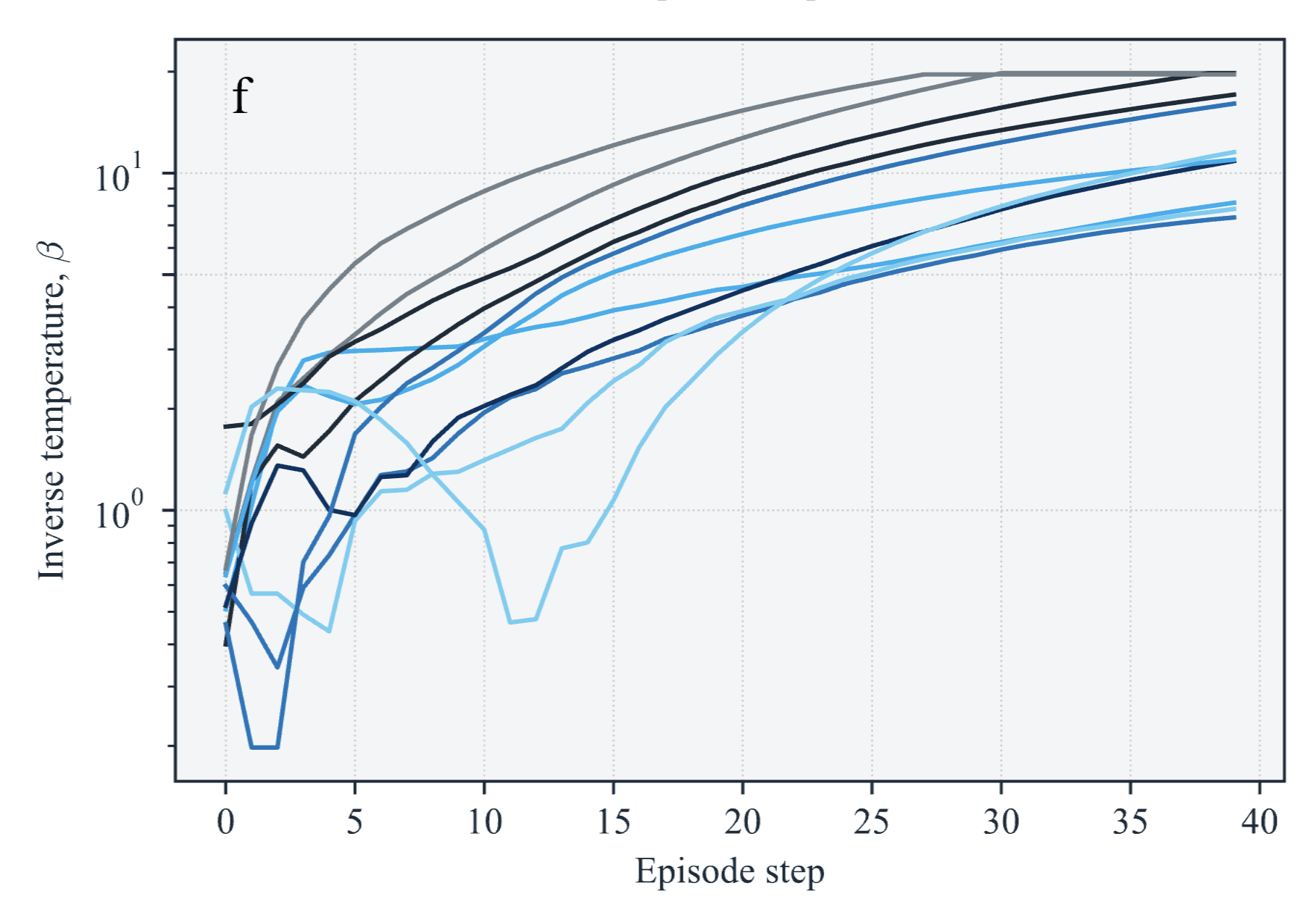
Analyzing the learnt policy
- Analysis of the learnt policy and taken actions strongly suggests that the RL agent relies on observed states to take actions.
- This indicates that the dynamical decision making has indeed achieved better results.
Conclusion
- Reinforcement Learning (RL) agents can be learnt to enhance classical Simulated Annealing (SA) strategies in solving Spin Glass problems.
- RL dynamically learns temperature schedules rather than relying on predefined heuristics that
- Achieves higher success rates in finding the ground state.
- Scales better with increasing system size.
- Generalizes well to different Hamiltonians.
Thanks!
deck
By Amin Mohamadi
deck
- 166



