Big O Notation/Time Complexity - Space Complexity
Andrés Bedoya G.
Social Engineering Specialist / Social Analyzer / Web Developer / Hardcore JavaScript Developer / Python - Nodejs enthusiastic
Big O Notation
WARNING
This section contains some math
Don't worry, we'll survive
Big O Notation
Imagine we have multiple implementations of the same function.
How can we determine which one is the "best"?
Big O Notation
Suppose we want to write a function that calculates the sum of all numbers from 1 up to (and including) some number n.
function addUpTo(n) {
let total = 0;
for (let i = 1; i <= n; i++) {
total += i;
}
return total;
}function addUpTo(n) {
return n * (n + 1) / 2;
}Which one is better?
Big O Notation
addUpTo(n) = 1 + 2 + 3 + ... + (n - 1) + n
+ addUpTo(n) = n + (n - 1) + (n - 2) + ... + 2 + 1
2addUpTo(n) = (n + 1) + (n + 1) + (n + 1) + ... + (n + 1) + (n + 1)
n copies
2addUpTo(n) = n * (n + 1)
addUpTo(n) = n * (n + 1) / 2
Big O Notation
function addUpTo(n) {
let total = 0;
for (let i = 1; i <= n; i++) {
total += i;
}
return total;
}
let t1 = performance.now();
addUpTo(1000000000);
let t2 = performance.now();
console.log(`Time Elapsed: ${(t2 - t1) / 1000} seconds.`)Timers...
Big O Notation
If not time, then what?
Rather than counting seconds, which are so variable...
Let's count the number of simple operations the computer has to perform!
Big O Notation
Counting Operations
function addUpTo(n) {
return n * (n + 1) / 2;
}3 simple operations, regardless of the size of n
1 multiplication
1 addition
1 division
Big O Notation
Counting Operations
function addUpTo(n) {
let total = 0;
for (let i = 1; i <= n; i++) {
total += i;
}
return total;
}n additions
n assignments
n additions and
n assignments
1 assignment
1 assignment
n comparisions
????
Big O Notation
Big O Notation is a way to formalize fuzzy counting
It allows us to talk formally about how the runtime of an algorithm grows as the inputs grow
Big O Notation
We say that an algorithm is O(f(n)) if the number of simple operations the computer has to do is eventually less than a constant times f(n), as n increases
- f(n) could be linear (f(n) = n)
- f(n) could be quadratic (f(n) = n2)
- f(n) could be constant (f(n) = 1)
- f(n) could be something entirely different!
Big O Notation
function addUpTo(n) {
return n * (n + 1) / 2;
}Always 3 operations
O(1)
function addUpTo(n) {
let total = 0;
for (let i = 1; i <= n; i++) {
total += i;
}
return total;
}Number of operations is (eventually) bounded by a multiple of n (say, 10n)
O(n)
Big O Notation
O(2n)
O(500)
O(13n2)
O(n)
O(1)
O(n2)
Big O Notation
function countUpAndDown(n) {
console.log("Going up!");
for (let i = 0; i < n; i++) {
console.log(i);
}
console.log("At the top!\nGoing down...");
for (let j = n - 1; j >= 0; j--) {
console.log(j);
}
console.log("Back down. Bye!");
}O(n)
O(n)
Number of operations is (eventually) bounded by a multiple of n (say, 2n)
O(n)
Big O Notation
function printAllPairs(n) {
for (var i = 0; i < n; i++) {
for (var j = 0; j < n; j++) {
console.log(i, j);
}
}
}O(n)
O(n)
O(n) operation inside of an O(n) operation.
O(n * n)
O(n2)
Big O Notation
- Arithmetic operations are constant
- Variable assignment is constant
- Accessing elements in an array (by index) or object (by key) is constant
- In a loop, the complexity is the length of the loop times the complexity of whatever happens inside of the loop
Big O Notation
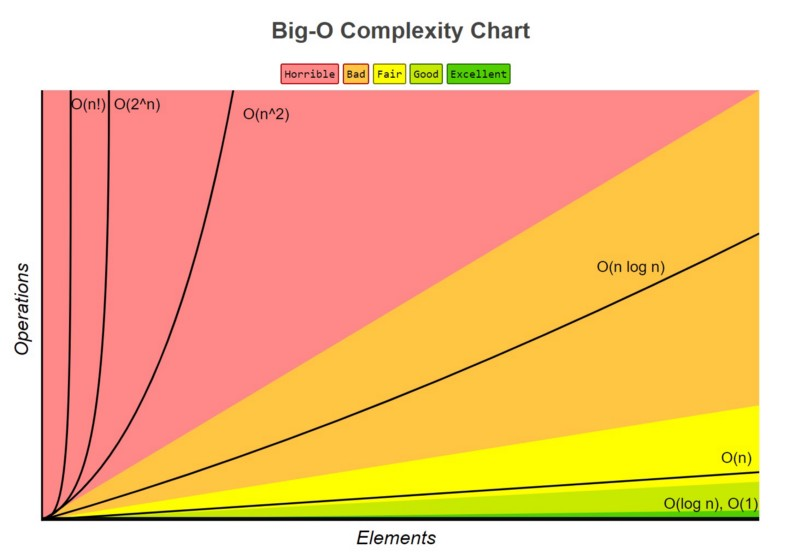
Big O Notation
Big O of Objects
- Insertion - O(1)
- Removal - O(1)
- Updating O(1)
- Searching - O(N)
- Access - O(1)
Big O of Object Methods
- Object.keys - O(N)
- Object.values - O(N)
- Object.entries - O(N)
- hasOwnProperty - O(1)
Big O of Arrays
- Insertion - It depends
- Removal - It depends
- Searching - O(N)
- Access - O(N)
Big O of Array Methods
- push - O(1)
- pop - O(1)
- shift - O(N)
- unshift - O(N)
- concat - O(N)
- slice - O(N)
- splice - O(N)
- sort - O(N * log N)
- forEach/map/filter/reduce/etc. - O(N)
Space Complexity
So far, we've been focusing on time complexity: how can we analyze the runtime of an algorithm as the size of the inputs increases?
We can also use big O notation to analyze space complexity: how much additional memory do we need to allocate in order to run the code in our algorithm?
Space Complexity
- Most primitives (booleans, numbers, undefined, null) are constant space
- Strings require O(n) space (where n is the string length)
- Reference types are generally O(n), where n is the length (for arrays) or the number of keys (for objects)
Space Complexity
function sum(arr) {
let total = 0;
for (let i = 0; i < arr.length; i++) {
total += arr[i];
}
return total;
}one number
another number
O(1) Space
Space Complexity
function double(arr) {
let newArr = [];
for (let i = 0; i < arr.length; i++) {
newArr.push(2 * arr[i]);
}
return newArr;
}n numbers
O(n) Space
Recap
- To analyze the performance of an algorithm, we use Big O Notation
- Big O Notation can give us a high level understanding of the time or space complexity of an algorithm
- Big O Notation doesn't care about precision, only about general trends (linear? quadratic? constant?)
- The time or space complexity (as measured by Big O) depends only on the algorithm, not the hardware used to run the algorithm
- Big O Notation is everywhere, so get lots of practice!
More info
Big O Notation
By Andrés BG
Big O Notation
Big O Notation/Time Complexity - Space Complexity
- 1,355



