Coloring of the graphs
Anna Powolny
dwdw
Subtitle
Graph Coloring?
- Special case of graph labeling
- Assignment of labels - colors - to elements of a graph
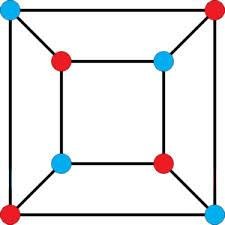
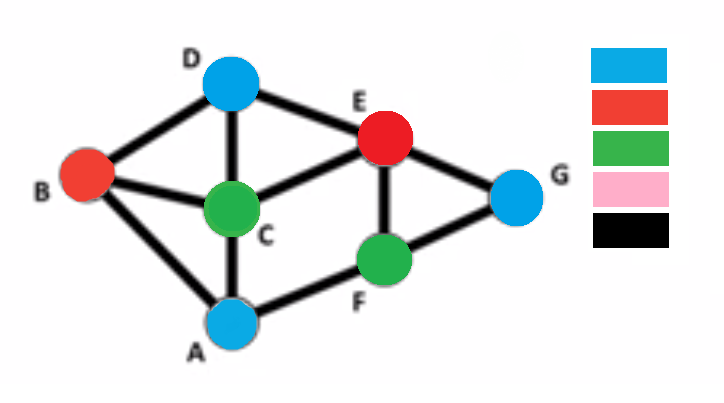
Vertex Coloring
Vertex Coloring
- no two vertices sharing the same edge have the same color.
- Graphs are loopless. (connection never directly back to itself)
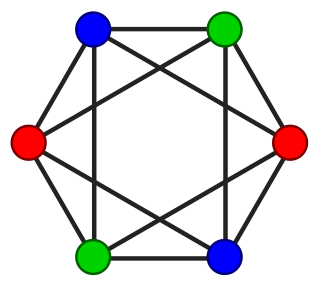
k-coloring
- coloring using at most k colors
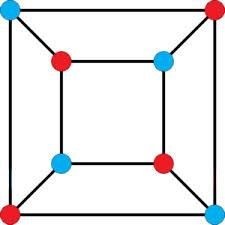
k-colorable
- graph having k-coloring (chromatic number χ(G)<=k)
chromatic number
- χ(G) - the smallest number of colors needed to color a graph G.
k-chromatic graph
- chromatic number χ(G) = k
one-colorable
Empty graph - isolated nodes with no edges.

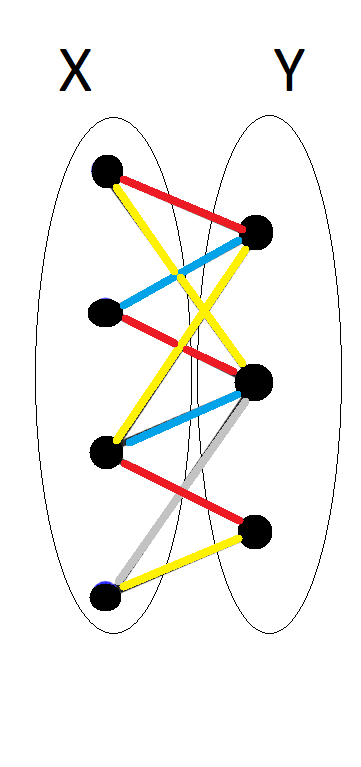
Bipartite Graph
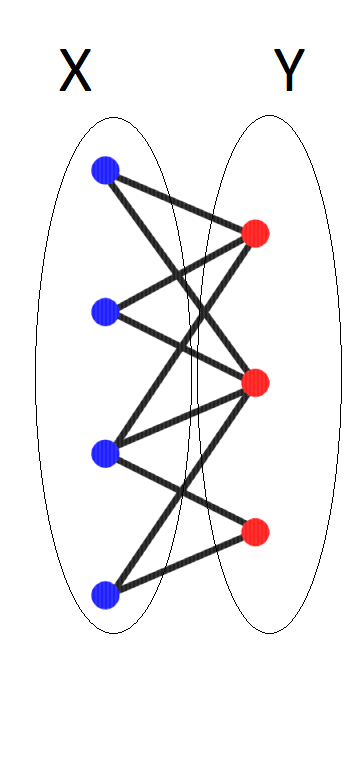
Two-colorable graph.
- vertices can be partioned into two sets X and Y
- each edge has one vertex in X and one in Y
color class
a subset of verticies assigned to the same color, every such a class forms an independent set.
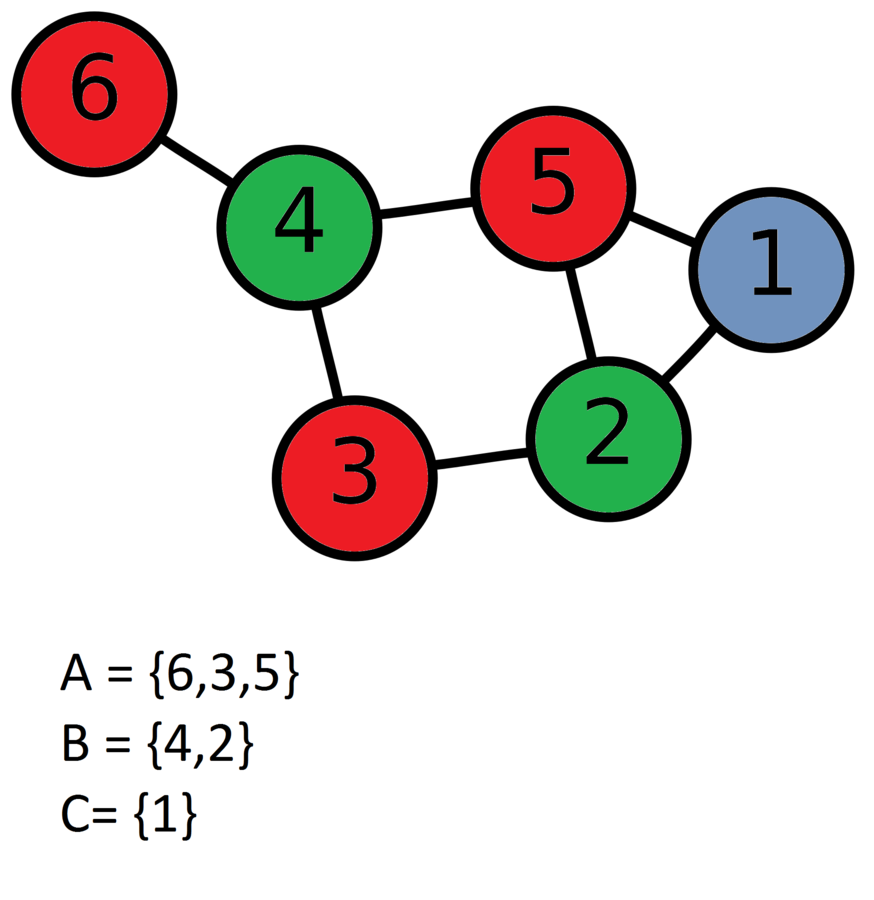
Edge Coloring
Edge Coloring
- no two adjacent edges share the same color
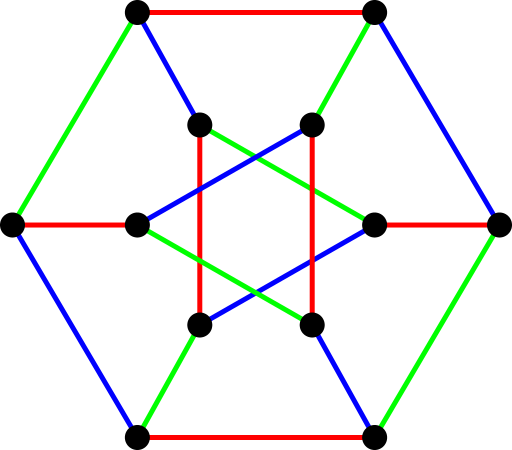
k-edge-coloring
coloring using at most k colors
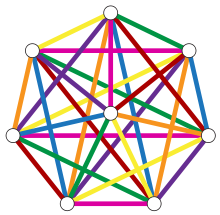
chromatic index
(edge chromatic number)
χ'(G) - the smallest number of colors needed for an edge coloring of a graph G.
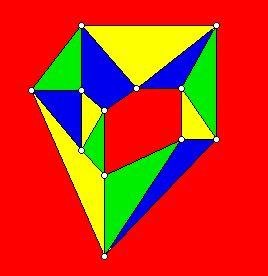
Face Coloring
Face Coloring
- no two faces that share a boundary have the same color
- Note the red color that goes to infinity.
Theorems
König's theorem for Bipartite Graph
χ'(G) = Δ(G)
χ'(G) - the smallest number of colors needed for an edge coloring of a graph G.
Δ(G) - maximum vertex degree
(maximum number of edges that vertex in graph G has.)
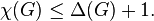
χ(G) - the smallest number of colors needed to color a graph. G.
Δ(G) - maximum vertex degree
(maximum number of edges that vertex in graph G has.)
Brooks Theorem
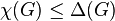
for a connected, simple graph G, unless G is a complete graph or an odd cycle.
Simple Graph
is an unweighted, undirected graph containing no graph loops or multiple edges

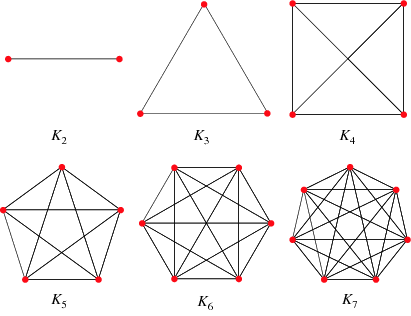
Complete Graph
is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge
Odd Cycle Graph
a cycle graph with an odd number of vertices.
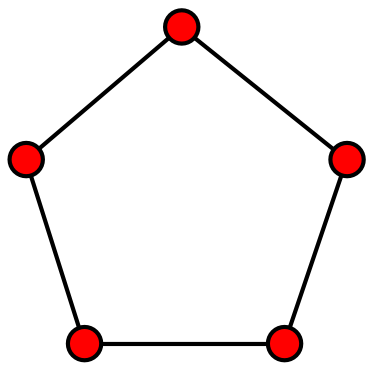
The Greedy Algorithm
- Choose an order for the vertices
- Choose a list of colors, also in some order
- In order, color each vertex using the first available color on the list, making sure that no two adjacent vertices have the same coloring
- Continue in this way until each vertex is colored
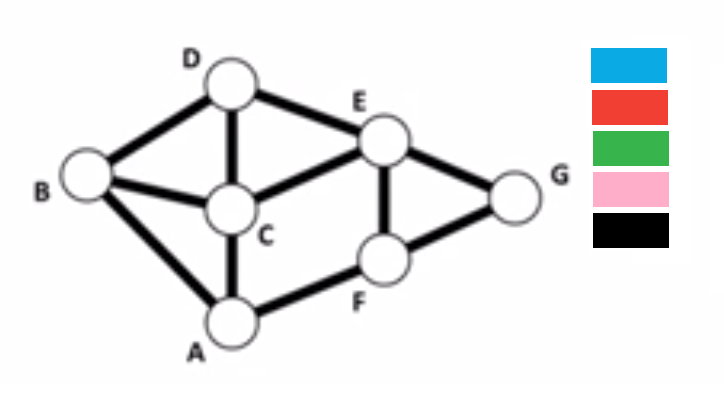
- Choose an order for the vertices
- Choose a list of colors, also in some order
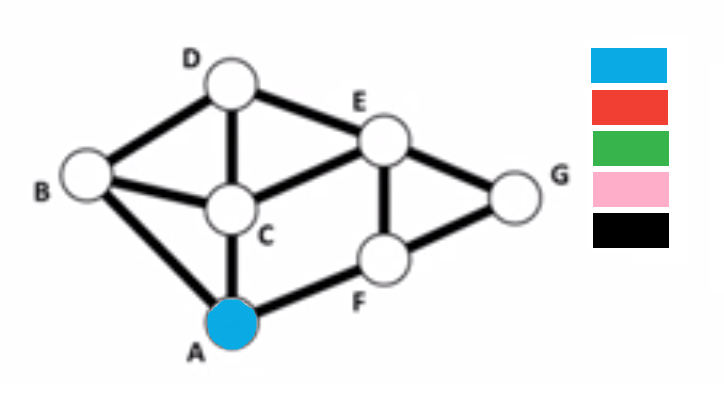
3. In order, color each vertex using the first available color on the list, making sure that no two adjacent vertices have the same coloring
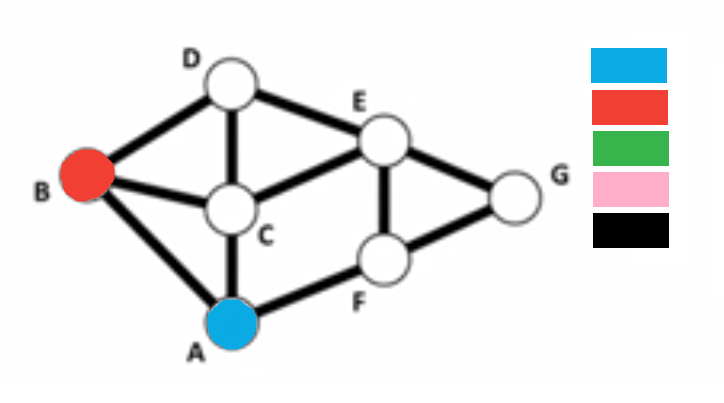
4. Continue in this way until each vertex is colored
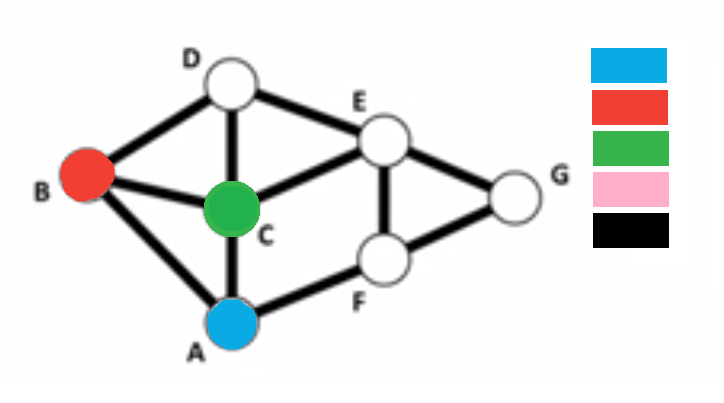
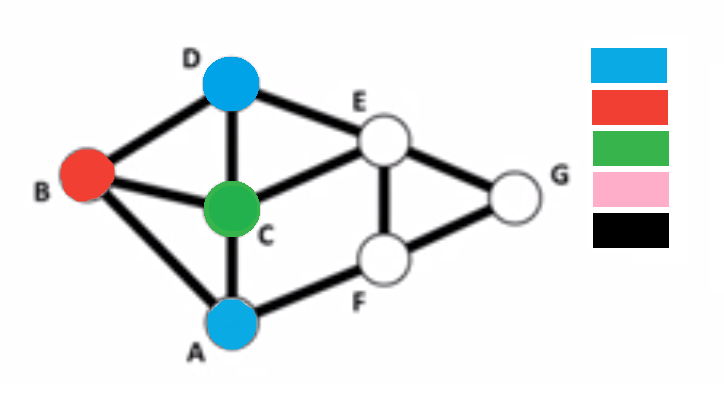
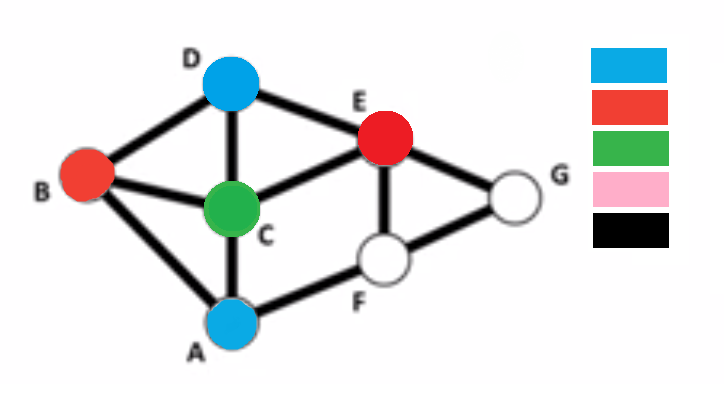
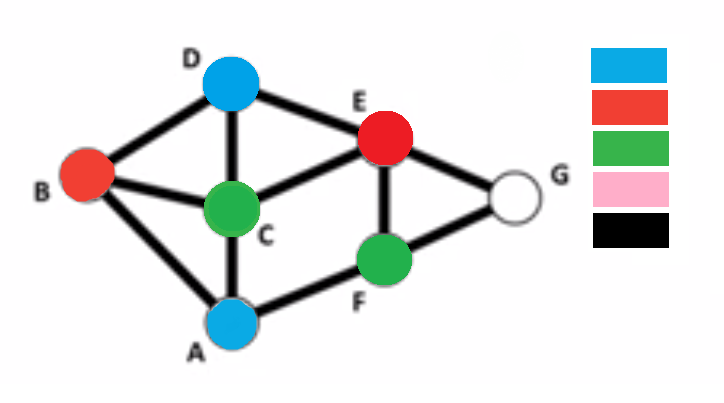
Applications
Scheduling
- a given set of jobs need to be assigned to time slots
- pairs of jobs may be in conflict in the sense that they may not be assigned to the same time slot
- vertex for every job and an edge for every conflicting pair of jobs
The chromatic number of the graph is the optimal time to finish all jobs without conflicts
Sudoku
- 81 blocks as 81 verticies
- digits from 1 to 9 as a 9 different colors
completing a 9-coloring on given specific graph with 81 vertices.
The End
Copy of deck
By aniamakota
Copy of deck
- 649



