Cellular Automata
What is it?
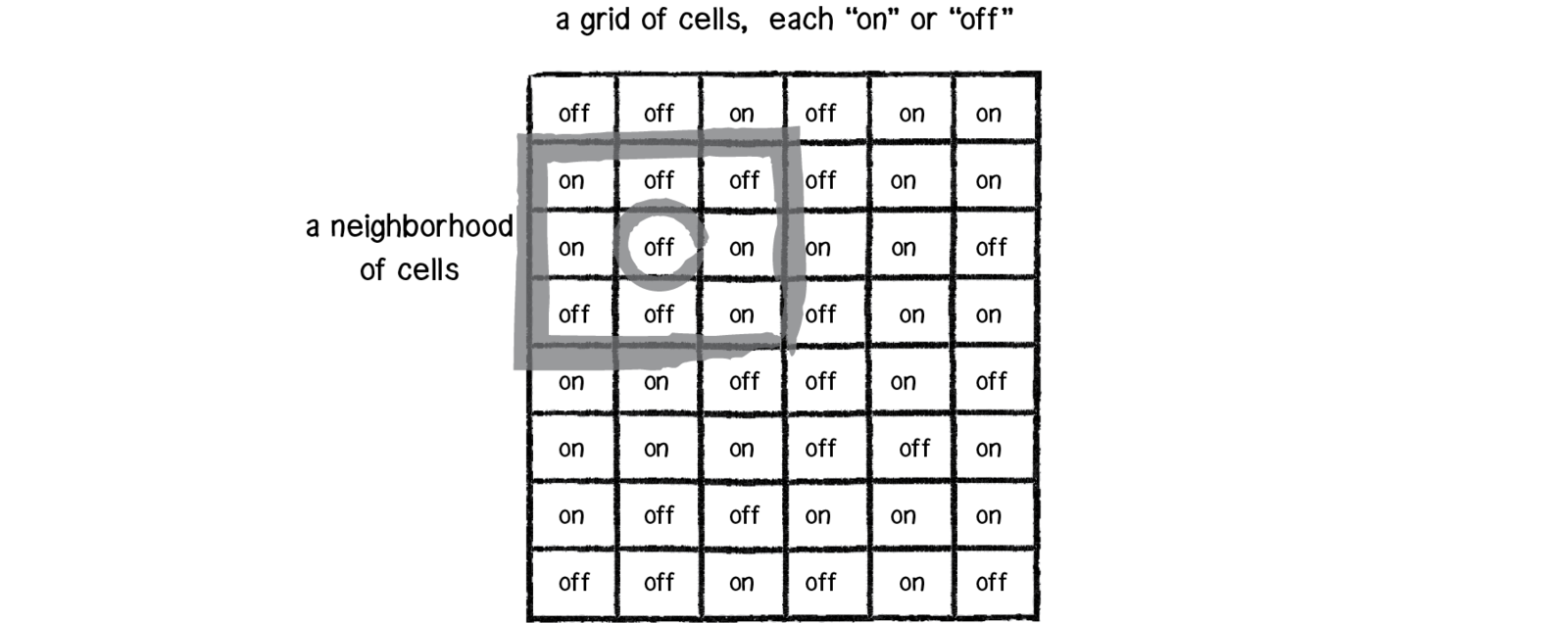
- The cells live on a grid.
- Each cell has a state. The number of state possibilities is typically finite. ( usually off and on )
- Each cell has a neighborhood. This can be defined in any number of ways, but it is typically adjacent cells.
Stanisław Ulam
Studying growth of crystals
John von Neumann
Imagining a world of self-replicating robots.
A New Kind of Science
Stephen Wolfram
Discusses how CA are not simply neat tricks, but are relevant to the study of biology, chemistry, physics, and all branches of science.
What is the simplest cellular automaton we can imagine?
Elementary CA
Grid. The simplest grid would be one-dimensional: a line of cells.

States. The simplest set of states would be two states: 0 or 1.

Neighborhood. The simplest neighborhood in one dimension for any given cell would be the cell itself and its two adjacent neighbors: one to the left and one to the right.

Time
Generations

CELL state at generation = f(CELL, neighbourhood at (generation - 1))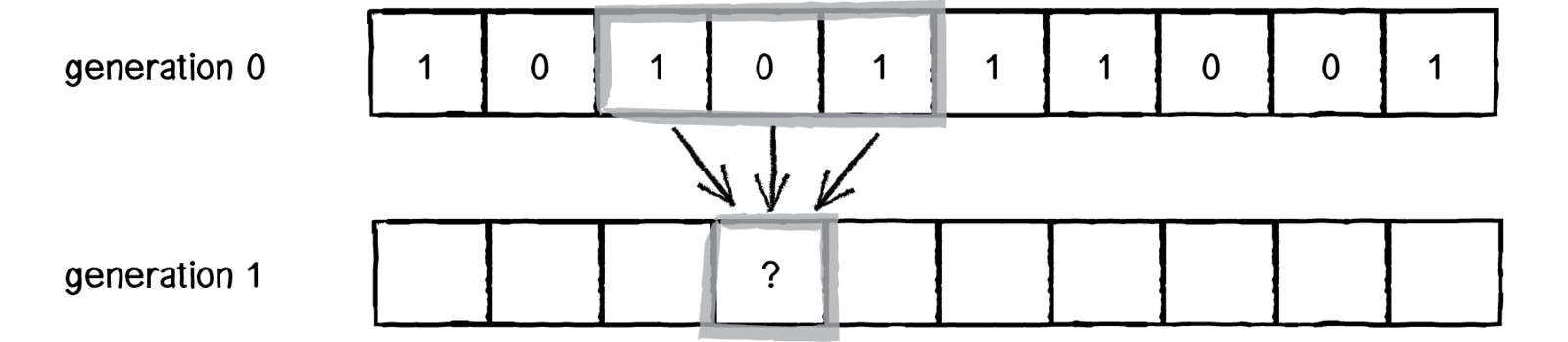
Blurring an image
A pixel’s new state (i.e. its color) is the average of all of its neighbors’ colors.
For Example
A cell’s new state is the sum of all of its neighbors’ states.
Another Example
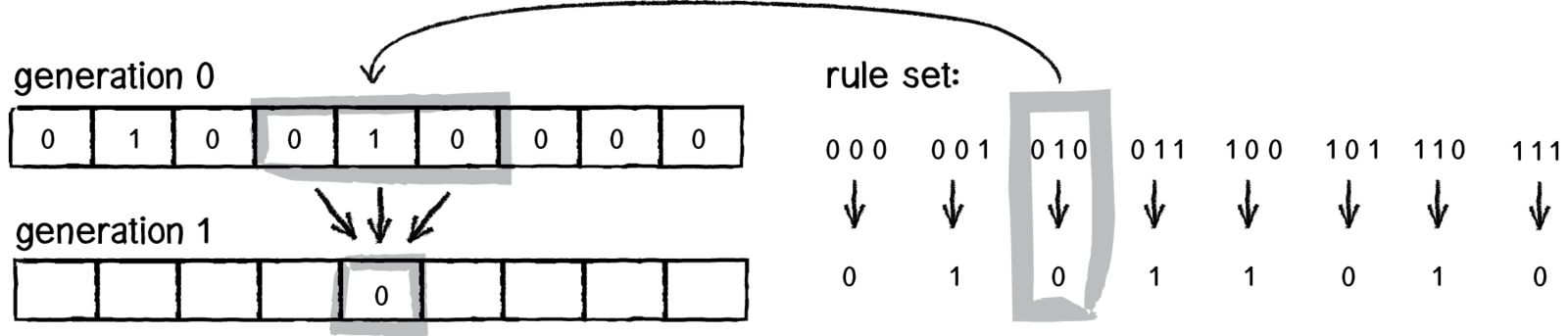
Wolfram’s elementary CA
Look at all the possible configurations of a cell and its neighbour and define the state outcome for every possible configuration.
Seems ridiculous?
We have three cells
How many possible ways can we configure the states?
Three cells define a 3 bit number

How high can you count with 3 bits?
Up to 8
Once we have defined all the possible neighborhoods,
we need to define an outcome (new state value: 0 or 1) for each neighbourhood configuration.

Standard Wolfram Model


Cellular Automata
By ..
Cellular Automata
- 2,224



