Maxout Networks

ICML'13

Ian J. Goodfellow - David Warde-Farley - Mehdi Mirza - Aaron Courville - Yoshua Bengio

Café de la Recherche #1 @Sicara

3 mai 2018 - Antoine Toubhans

Abstract

We consider the problem of designing models to leverage a recently introduced approximate model averaging technique called dropout. We define a simple new model called maxout (so named because its output is the max of a set of inputs, and because it is a natural companion to dropout) designed to both facilitate optimization by dropout and improve the accuracy of dropout’s fast approximate model averaging technique. We empirically verify that the model successfully accomplishes both of these tasks. We use maxout and dropout to demonstrate state of the art classification performance on four benchmark datasets: MNIST, CIFAR-10, CIFAR100, and SVHN.

A regularization technique for NN

The paper's thesis

Benchmarks

Maxout Networks

  1. Introduction
  2. Review of dropout
  3. Description of maxout
  4. Maxout is a universal approximator
  5. Benchmark results
  6. Comparison to rectifiers
  7. Model averaging
  8. Optimization
  9. Conclusion

Maxout Networks

  1. Introduction
  2. Review of dropout
  3. Description of maxout
  4. Maxout is a universal approximator
  5. Benchmark results
  6. Comparison to rectifiers
  7. Model averaging
  8. Optimization
  9. Conclusion

Maxout Networks

  1. Introduction
  2. Review of dropout
  3. Description of maxout
  4. Maxout is a universal approximator
  5. Benchmark results
  6. Comparison to rectifiers
  7. Model averaging
  8. Optimization
  9. Conclusion

Dropout: a bagging technique

Dropout training is similar to bagging. [2]

[2] Breiman, Leo. Bagging predictors. Machine Learning, 24 (2):123–140, 1994

BAGGING = Bootstrap AGGregatING

 

Train different models on different subsets of the data

e.g. random forest is bagging of decision trees

 Bagging overview

\mathbb{E}\left[\left(\frac{1}{N}\sum_i\varepsilon_i\right)^2\right] = \frac{1}{N^2} \mathbb{E}\left[ \sum_i \varepsilon_i^2 + \sum_{i \neq j}\varepsilon_i\varepsilon_j \right]
E[(1N∑iεi)2]=1N2E[∑iεi2+∑i≠jεiεj]\mathbb{E}\left[\left(\frac{1}{N}\sum_i\varepsilon_i\right)^2\right] = \frac{1}{N^2} \mathbb{E}\left[ \sum_i \varepsilon_i^2 + \sum_{i \neq j}\varepsilon_i\varepsilon_j \right]
  • a regularization technique
  • key idea: different models will not make the same errors on the test set
= \frac{1}{N} V + \frac{N-1}{N} C
=1NV+N−1NC= \frac{1}{N} V + \frac{N-1}{N} C
\mathbb{E}\left[\varepsilon_i\right] = 0 \quad V = \mathbb{E}\left[\varepsilon_i^2\right] \quad C = \mathbb{E}\left[\varepsilon_i\varepsilon_j\right]
E[εi]=0V=E[εi2]C=E[εiεj]\mathbb{E}\left[\varepsilon_i\right] = 0 \quad V = \mathbb{E}\left[\varepsilon_i^2\right] \quad C = \mathbb{E}\left[\varepsilon_i\varepsilon_j\right]

Error of the i-th model on the test set: 

\varepsilon_i
εi\varepsilon_i

 Dropout overview

Approximation of bagging an exponentially large number of neural networks.

  • the sub-models share parameters
  • approximated inference (weight scaling inference rule)

 Dropout overview

Training an ensemble of NN

For each training example:

  • randomly sample a mask      
  • the probability of each entry being 1 is a hyperparameter
  • stochastic training
  • feedforward and backprop as usual
p(y\vert x; \theta)
p(y∣x;θ)p(y\vert x; \theta)
\mu
μ\mu
p(y\vert x;\theta,\mu)
p(y∣x;θ,μ)p(y\vert x;\theta,\mu)

 Dropout inference

p(y\vert x;\theta) = \sum_\mu p(\mu) p(y\vert x;\theta,\mu)
p(y∣x;θ)=∑μp(μ)p(y∣x;θ,μ)p(y\vert x;\theta) = \sum_\mu p(\mu) p(y\vert x;\theta,\mu)

Arithmetic mean:

Untractable!

 Dropout inference

\hat{p}(y\vert x;\theta) = \Pi_\mu p(y\vert x;\theta,\mu)^{p(\mu)}
p^(y∣x;θ)=Πμp(y∣x;θ,μ)p(μ)\hat{p}(y\vert x;\theta) = \Pi_\mu p(y\vert x;\theta,\mu)^{p(\mu)}

Geometic mean:

The trick: use geometric mean instead

p(y\vert x;W, b,\mu) = \text{softmax}(W^T(x \circ \mu)+b)_y
p(y∣x;W,b,μ)=softmax(WT(x∘μ)+b)yp(y\vert x;W, b,\mu) = \text{softmax}(W^T(x \circ \mu)+b)_y

If

Then

p(y\vert x;W,b) = \text{softmax}(\frac{1}{2}W^Tx+b)_y
p(y∣x;W,b)=softmax(12WTx+b)yp(y\vert x;W,b) = \text{softmax}(\frac{1}{2}W^Tx+b)_y

Approximations:

  • Geometric mean vs arithmetic mean
  • Theoretical proof for one layer only 

the weight scaling rule

works well empirically

 Dropout inference - Sketch of proof

p(\mu) = \frac{1}{2^d}
p(μ)=12dp(\mu) = \frac{1}{2^d}
\propto \left( \Pi_\mu \text{softmax}(W^T(x \circ \mu)+b)_y \right) ^{2^{-d}}
∝(Πμsoftmax(WT(x∘μ)+b)y)2−d\propto \left( \Pi_\mu \text{softmax}(W^T(x \circ \mu)+b)_y \right) ^{2^{-d}}
p(y\vert x;W,b) \propto \Pi_\mu p(y\vert x;W,b,\mu)^{p(\mu)}
p(y∣x;W,b)∝Πμp(y∣x;W,b,μ)p(μ)p(y\vert x;W,b) \propto \Pi_\mu p(y\vert x;W,b,\mu)^{p(\mu)}
\text{softmax}(z)_y = \frac{e^{z_y}}{\sum_{y'}e^{z_{y'}}}
softmax(z)y=ezy∑y′ezy′\text{softmax}(z)_y = \frac{e^{z_y}}{\sum_{y'}e^{z_{y'}}}
\propto \left( \Pi_\mu \text{exp}(W^T(x \circ \mu)+b)_y \right) ^{2^{-d}}
∝(Πμexp(WT(x∘μ)+b)y)2−d\propto \left( \Pi_\mu \text{exp}(W^T(x \circ \mu)+b)_y \right) ^{2^{-d}}
\propto \text{exp} \left( 2^{-d} \sum_\mu (W^T(x \circ \mu)+b)_y \right)
∝exp(2−d∑μ(WT(x∘μ)+b)y)\propto \text{exp} \left( 2^{-d} \sum_\mu (W^T(x \circ \mu)+b)_y \right)
\propto \text{exp} \left( \frac{1}{2} (W^Tx+b )_y \right)
∝exp(12(WTx+b)y)\propto \text{exp} \left( \frac{1}{2} (W^Tx+b )_y \right)
= \text{softmax} \left( \frac{1}{2} (W^Tx+b ) \right)_y
=softmax(12(WTx+b))y= \text{softmax} \left( \frac{1}{2} (W^Tx+b ) \right)_y

Maxout Networks

  1. Introduction
  2. Review of dropout
  3. Description of maxout
  4. Maxout is a universal approximator
  5. Benchmark results
  6. Comparison to rectifiers
  7. Model averaging
  8. Optimization
  9. Conclusion

"Maxout units can be seen as learning the activation function itself" [2]

Maxout units: a generalization of ReLU

 [2] Deep Learning Book,  p188.

"The maxout model is simply a feed-forward architecture[...] that uses a new type of activation function: the maxout unit." [1]

[1] ICML'13, Maxout networks, Goodfellow and Al.

Maxout units: a generalization of ReLU

\text{ReLU}(z) = \text{max}(0, z)
ReLU(z)=max(0,z)\text{ReLU}(z) = \text{max}(0, z)

How to compare activation functions:

  • saturation
  • piecewise linear
  • bounded
  • sparse activation [3]

 [3] Deep Sparse Rectifier Neural Networks, Bengio and Al.

x \in \mathbb{R}^d, \quad W \in \mathbb{R}^{d \times m}, \quad b \in \mathbb{R}^m
x∈Rd,W∈Rd×m,b∈Rmx \in \mathbb{R}^d, \quad W \in \mathbb{R}^{d \times m}, \quad b \in \mathbb{R}^m

Hidden Layer + ReLU

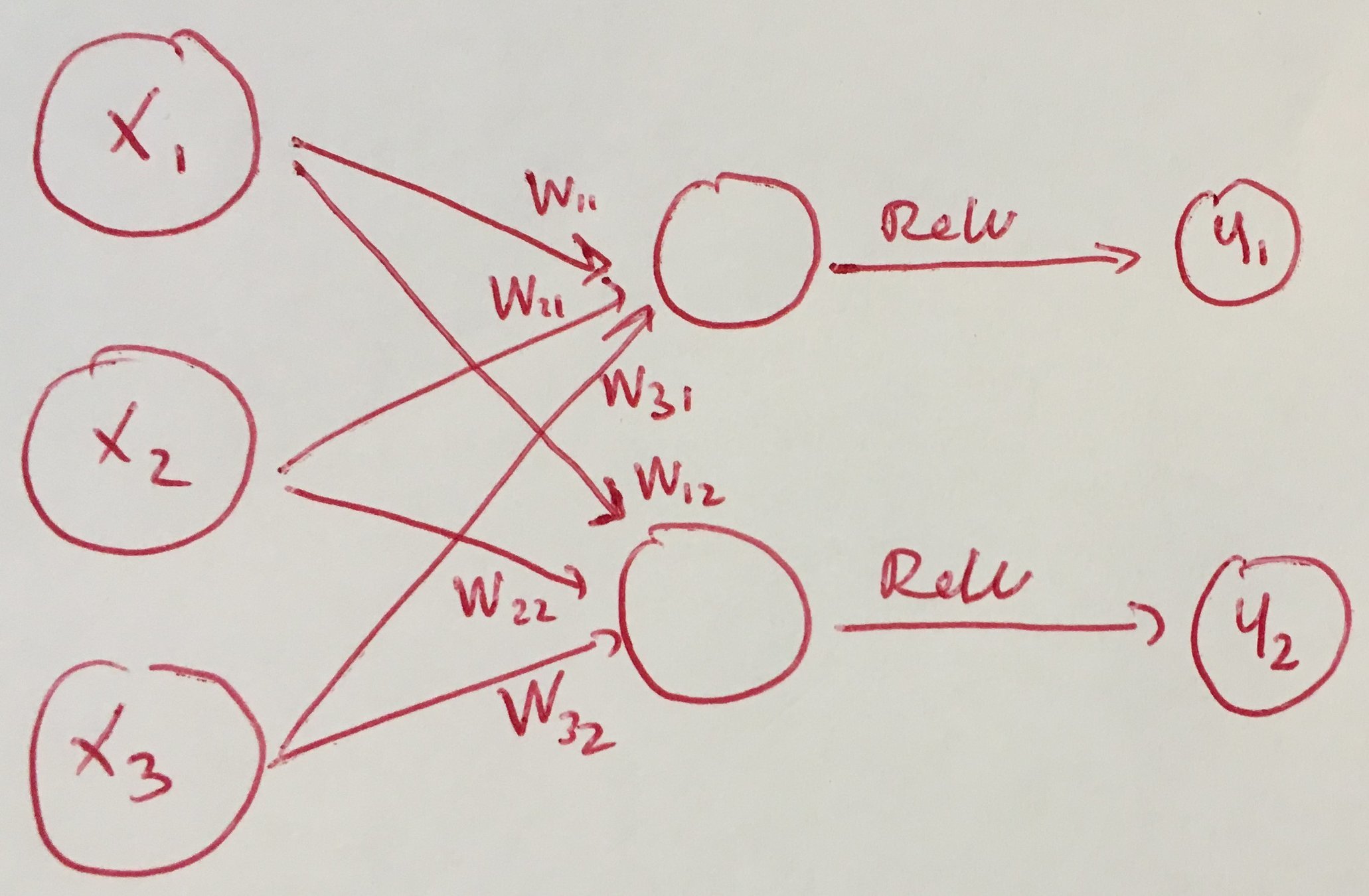
y = \text{ReLU}\left( W^Tx + b \right) \in \mathbb{R}^m
y=ReLU(WTx+b)∈Rmy = \text{ReLU}\left( W^Tx + b \right) \in \mathbb{R}^m

Maxout definition

z = x^TW + b \in \mathbb{R}^{m \times k} \quad y_i = \text{max}_{j\in[1, k]}(z_{ij})
z=xTW+b∈Rm×kyi=maxj∈[1,k](zij)z = x^TW + b \in \mathbb{R}^{m \times k} \quad y_i = \text{max}_{j\in[1, k]}(z_{ij})
x \in \mathbb{R}^d, \quad W \in \mathbb{R}^{d \times m \times k}, \quad b \in \mathbb{R}^{m \times k}
x∈Rd,W∈Rd×m×k,b∈Rm×kx \in \mathbb{R}^d, \quad W \in \mathbb{R}^{d \times m \times k}, \quad b \in \mathbb{R}^{m \times k}

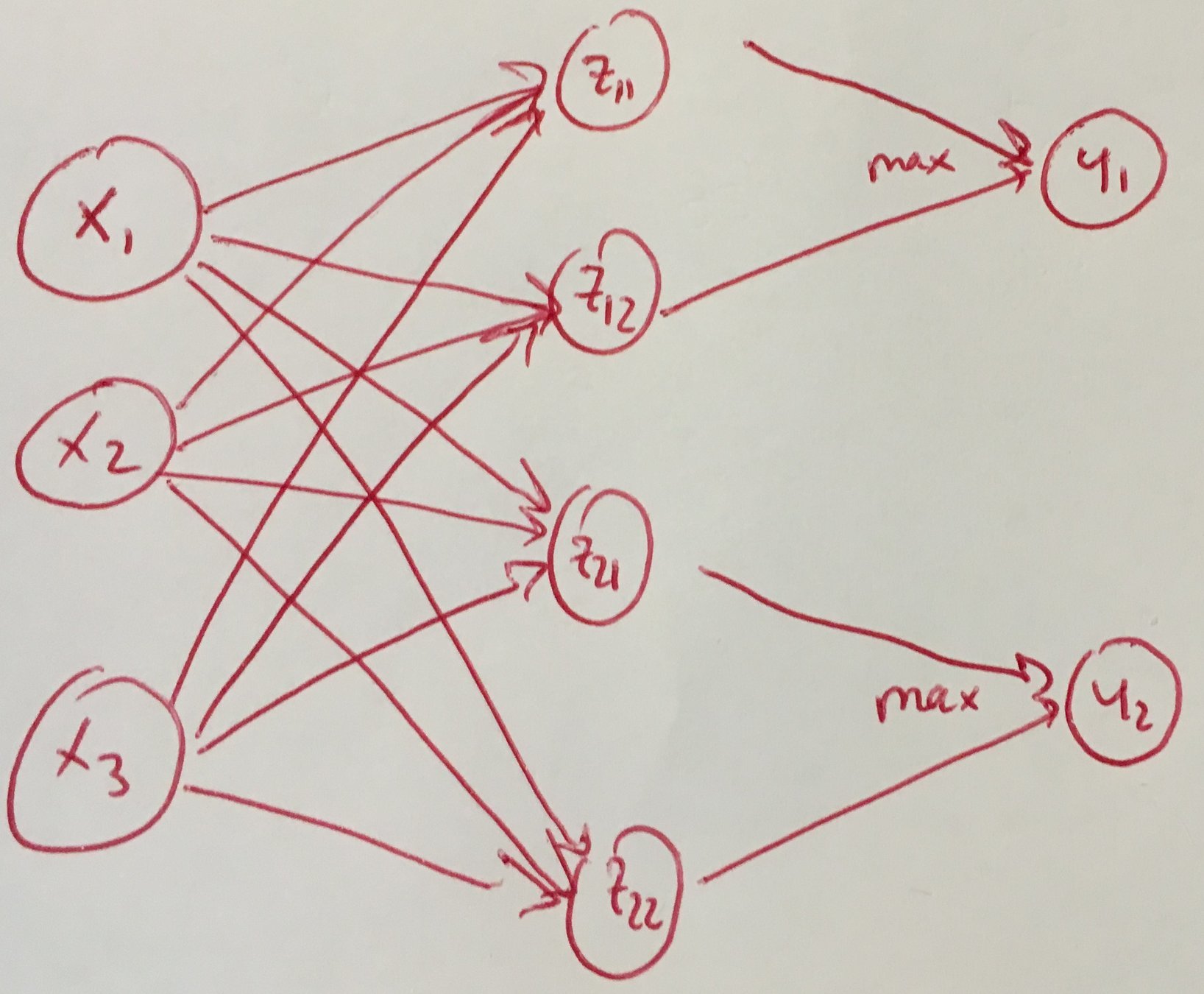
Maxout definition

Maxout for CNN

In a convolutional network, a maxout feature map can be constructed by taking the maximum across k affine feature maps (i.e., pool across channels, in addition spatial locations).

Maxout      Max-pooling !

\neq
≠\neq
  • (2D) Max-pooling: only across spatial dimensions
  • Maxout: across all dimension (channels and spacial)

Channel pooling

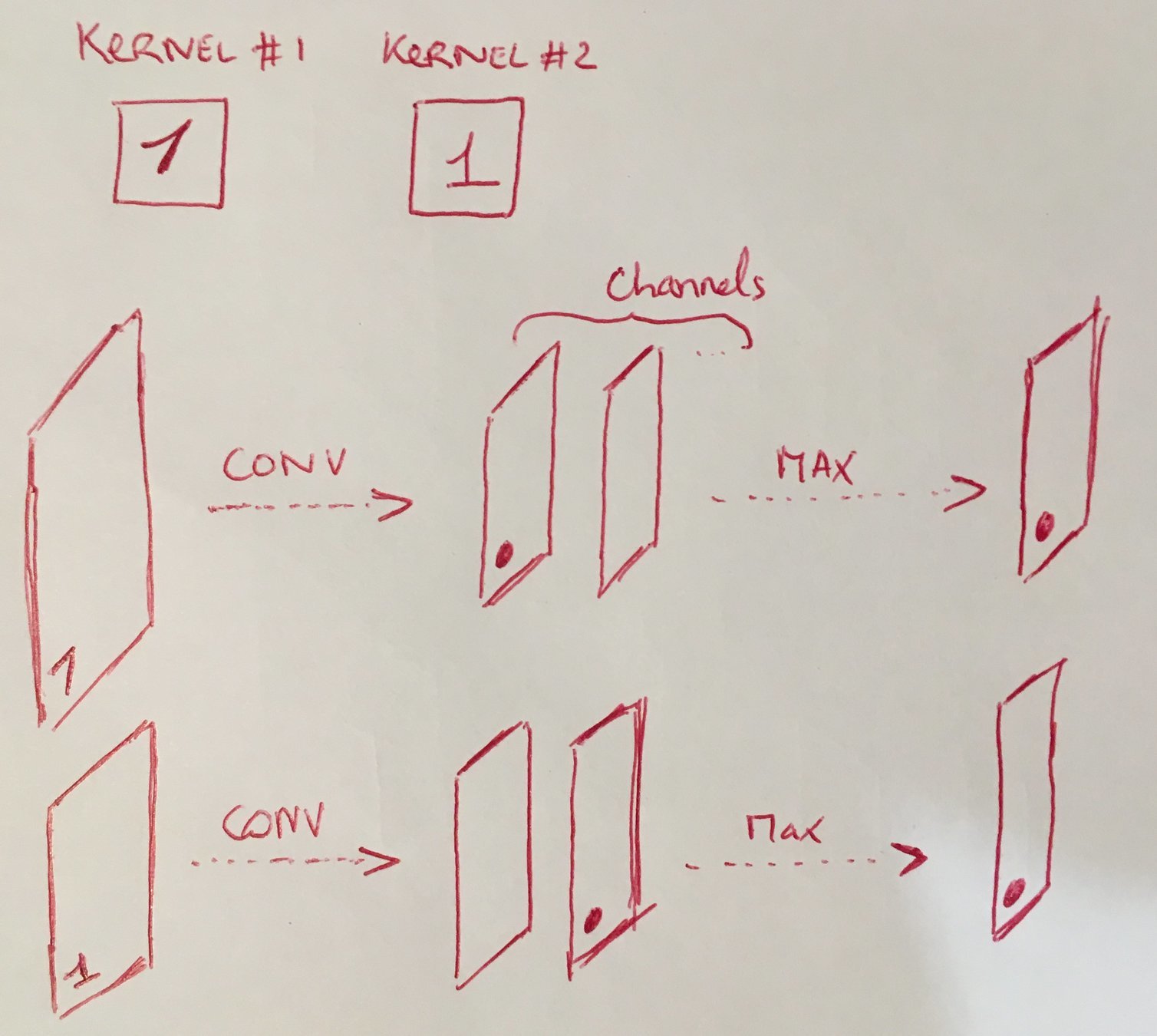
Maxout for CNN

Maxout Networks

  1. Introduction
  2. Review of dropout
  3. Description of maxout
  4. Maxout is a universal approximator
  5. Benchmark results
  6. Comparison to rectifiers
  7. Model averaging
  8. Optimization
  9. Conclusion

A Universal Approximator

Any feedforward NN with one hidden layer with any "squashing" activation function and a linear out is a universal approximator [5]

 [5] Multilayer feedforward networks are universal approximators, Hornik and Al., 1989

 One-layer perceptron can not represent the Xor function [4]

 [4] Minsky and Papert, 1969

*

(*) provided sufficiently many hidden units are available

A Universal Approximator

Sketch of proof

Sketch of proof

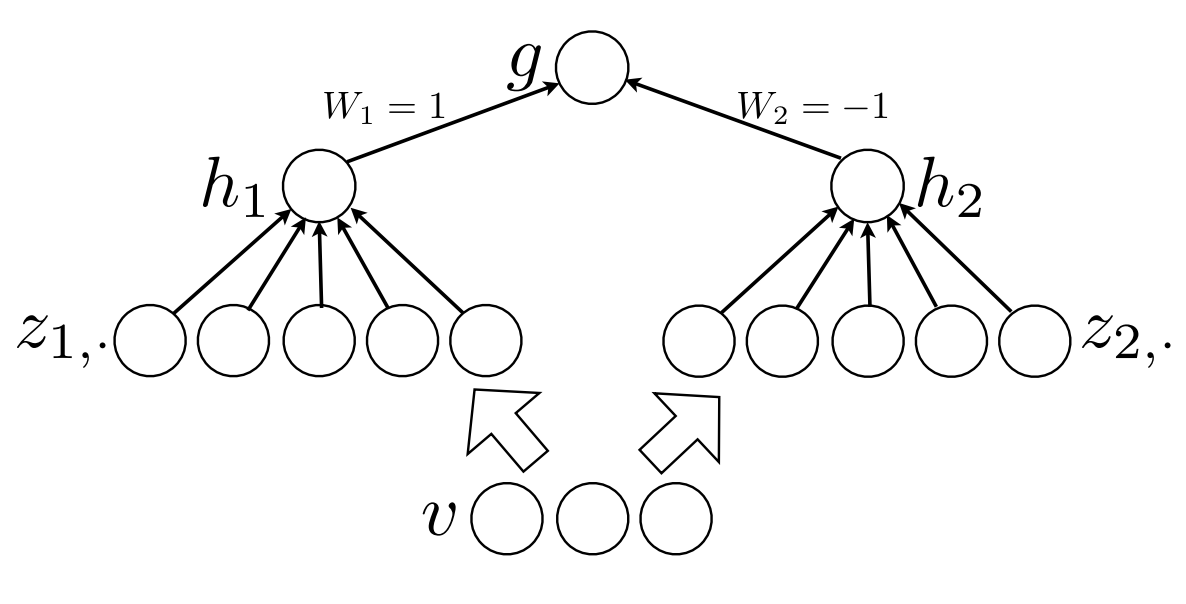
Maxout Networks

  1. Introduction
  2. Review of dropout
  3. Description of maxout
  4. Maxout is a universal approximator
  5. Benchmark results
  6. Comparison to rectifiers
  7. Model averaging
  8. Optimization
  9. Conclusion

Benchmark results

MNIST

60000 x 28 x 28 x 1

10 classes

4 datasets, comparison to the state of the art (2013)

CIFAR-10

60000 x 32 x 32 x 3

10 classes

CIFAR-100

60000 x 32 x 32 x 3

100 classes

SVHN

>600K x 32 x 32 x 3

Identify digits in the images

Benchmark results - MNIST

The permutation invariant version:

  • should be unaware of the 2D structure, meaning no convolution
  • 2 dense Maxout layers + softmax
  • dropout regularization
  • best result without the use of unsupervised pretraining.

Benchmark results - MNIST

The CNN version:

  • 3 convolutional maxout layers + 1 dense layer + softmax

Benchmark results

  • Other results in the paper
  • Dropout + Maxout achieve state of the art performance

Maxout Networks

  1. Introduction
  2. Review of dropout
  3. Description of maxout
  4. Maxout is a universal approximator
  5. Benchmark results
  6. Comparison to rectifiers
  7. Model averaging
  8. Optimization
  9. Conclusion

Comparison to rectifiers

Why are the results better?

  • improved preprocessing
  • larger models
  • use of Maxout?

Comparison to rectifiers

4 models

  1. Medium-size Maxout network
  2. Rectifier network wit cross-channel pooling with the same # of parameters
  3. Rectifier network with the same # of units (fewer parameters)
  4. Large rectifier with the same # of parameters

Cross-validation for choosing learning rate and momentum

Maxout Networks

  1. Introduction
  2. Review of dropout
  3. Description of maxout
  4. Maxout is a universal approximator
  5. Benchmark results
  6. Comparison to rectifiers
  7. Model averaging
  8. Optimization
  9. Conclusion

Model averaging

Having demonstrated that maxout networks are effective models, we now analyze the reasons for their success. We first identify reasons that maxout is highly compatible with dropout’s approximate model averaging technique

Dropout averaging sub-models = divide weight by 2

  • Exact for a single layer + softmax
  • Approximation for multilayers​​
  • ​​But it remains exact for multiple linear layers

The author's hypothesis:  dropout training encourages Maxout units to have large linear regions around inputs that appear in the training data.

Model averaging

Empirical verification:

Maxout Networks

  1. Introduction
  2. Review of dropout
  3. Description of maxout
  4. Maxout is a universal approximator
  5. Benchmark results
  6. Comparison to rectifiers
  7. Model averaging
  8. Optimization
  9. Conclusion

Optimization

The second key reason that maxout performs well is that it improves the bagging style training phase of dropout.

The author hypothesis: when trained with dropout, Maxout is easier to optimize than rectified linear units with cross-channel pooling.

  • Maxout unit does not include 0
  • Performance gets worse when including 0

Optimization

Empirical verification I:

Optimization - Saturation

Empirical verification II:

Who's next? What's next?

 

You decide.

Café de la Recherche #1 - Maxout networks

Café de la Recherche #2 - ???

Maxout Networks

By Antoine Toubhans

Made with Slides.com

Maxout Networks

  • 1,150

More from Antoine Toubhans