module 2 : Comparer plusieurs séries statistiques
Y-a-t-il une relation entre les séries (statistiques) ?
1 jour
2 + 2 jours
5 jours
module 2.1 : Y-a-t-il une relation entre les séries (statistiques) ?
Support de formation en ligne:
Suivre le diaporama en direct:
Télécharger LibreOffice (si nécessaire):
https://fr.libreoffice.org/download/telecharger-libreoffice/
Télécharger
et
(si nécessaire)
jour 1- présentation, rappels, vocabulaire, théorie
jour 2 - Deux variables Quantitatives
- Deux séries d'une même variable
Jour 3 - exercices pratiques sur les variables quantitatives
- Une variable Quantitative & une variable Qualitative (ANOVA)
jour 4 - Deux variables Qualitatives
jour 5 - Super Exo
module 2.1 : Y-a-t-il une relation entre les séries (statistiques) ?
1.1.1. Rappel stat 1: Vocabulaire
POPULATION
C’est l’ensemble des individus sur lesquels porte notre étude
Ex: les céramiques antiques, les tombes d’une nécropole,…
ÉCHANTILLON
C’est un sous-ensemble de la population, réellement accessible à l’expérimentateur.
Ex: les tombes fouillées, les céramiques prélevées et enregistrées
Attention on parle parfois de population pour désigner notre échantillon statistique
INDIVIDU
C’est une entité élémentaire sur laquelle on va mesurer ou observer des phénomènes
Ex: le tesson de bord de la dressel 234 qui fait 2cm d’épaisseur, la tombe 312
i
1.1.1. Vocabulaire
VARIABLE ou CARACTÈRE
C’est une propriété commune à tous les individus d’une population.
Ex: pour des céramiques: le type, la datation / pour des squelettes: leur sexe, leur taille, leur position,…
MODALITÉ
C’est la valeur ou la situation prise par une variable pour un individu
Ex: pour une céramique: dressel 657, LT2b pour un squelette: M, 180 cm, NE
TABLEAU ÉLÉMENTAIRE
C’est un tableau à double entrée où les lignes correspondent aux individus et les colonnes aux variables décrivant ces éléments.
1.1.1. Vocabulaire
ROBUSTESSE
En statistiques, la robustesse d'un estimateur est sa capacité à ne pas être perturbé par une modification dans une petite partie des données.
FIABILITÉ
C'est un indicateur de confiance. Il sert à confirmer que les différences enregistrées entre les versions testées ne sont pas le fruit du hasard.
PUISSANCE
La puissance statistique d'un test est la probabilité de rejeter l'hypothèse nulle.
1.1.1. Vocabulaire
VARIANCE
La variance est une mesure qui permet de tenir compte de la dispersion de toutes les valeurs d'un ensemble de données.
TABLEAU DE DÉNOMBREMENT
Le tableau de dénombrement donne un résumé numérique d'une distribution statistique. La construction du tableau de dénombrement et des représentations graphiques sera différente selon que le caractère étudié quantitatif discret, quantitatif continu, ou qualitatif.
1.1.2. Nature d'une variable
une variable peut être
Qualitative
Les modalités expriment l'appartenance à une catégorie.
Ex: type de fait, période chrono, présence ou absence d’une carie sur une dent
Quantitative
Les modalités s'expriment en nombres réels.
Il est possible de les ordonner et de faire des calculs dessus.
Ex: longueur d’un fait, NR, NMI, Taux de fragmentation
Vocabulaire: exercice
-
Définir la population ?
-
Définir l'échantillon ?
-
Les individus ?
-
Déterminer la nature de chaque variable ?
clic pour visualiser le tableau d'exercice
1.1.3. Distribution des données quantitatives
DISTRIBUTION
Une distribution correspond à la répartition dans son ensemble de toutes les valeurs possibles d’une même variable.
1.1.3 Distribution des données quantitatives
Variable Quantitative Continue :
LA LOI NORMALE
La loi normale (gaussienne, cloche…) est une loi de probabilité utilisée pour rendre compte des variations aléatoires.
1.1.3 Distribution des données quantitatives
LA LOI NORMALE
Elle est théorisée à partir du 17e siècle lorsque les mathématiciens s’intéressent aux lois de probabilité avec pour modèle les jeux de hasard (dés, pile/face..).
Carl Friedrich Gauss (1777-1855)
Tableau de Gottlieb Biermann (1887), d'après un portrait par Christian Albrecht Jensen (1840).
Abraham de Moivre (1667-1754)
portrait d'après un buste e Bloomsbanp square, relevé par Faber et imprimé par Jos Highmore en 1736.
Pierre Simon de Laplace (1749-1827)
gravure de James Posselwhite (XIXe s.)
1.1.3 Distribution des données quantitatives
LA LOI NORMALE
Sa formule est :
Elle est définie par deux paramètres : l’espérance (μ) et l’écart-type (σ)
Elle est unimodale : la moyenne, la médiane et le mode y sont égaux
Elle est symétrique autour de la moyenne
1.1.3 Distribution des données quantitatives
LA LOI NORMALE
Entre 1 écart-type avant et 1 écart-type après la moyenne correspond à 68 % de l’aire sous la courbe
Entre 2 écart-types avant et 2 écart-types après la moyenne correspond à 95 % de l’aire sous la courbe
Entre 3 écart-types avant et 3 écart-types après la moyenne correspond à 99 % de l’aire sous la courbe
1.1.3 Distribution des données quantitatives
LA LOI NORMALE
Sa modélisation par d'une expérience binomiale (problème à deux solutions)
répétée plusieurs fois, comme le lancer d’une pièce de monnaie
1.1.3 Distribution des données quantitatives
LA LOI NORMALE
1.1.3 Distribution des données quantitatives
LA LOI NORMALE
1.1.3 Distribution des données quantitatives
LA LOI NORMALE
On peut visualiser la courbe en vrai avec l'expérience de la planche de Galton
https://duckduckgo.com/?q=Probability+Demonstration%3A+the+Galton+Board&t=ffab&iar=videos&iax=videos&ia=videos
1.1.3 Distribution des données quantitatives
LA LOI NORMALE
La loi normale sert de référence pour étudier, modéliser ou comparer toute distribution dont on suppose qu'elle est soumise à des variations aléatoire, "au hasard"
1.1.3 Distribution des données quantitatives
Le théorème central limite :
est la convergence de la somme d'une suite de variables aléatoires vers la loi normale
Par Cmglee — Travail personnel, CC BY-SA 3.0
Exemple obtenu à partir de jets
de 1 à plusieurs dés (n)
1.1.4. Rappel: utilisation de R
1. Ouvrir Rstudio
2. Définir le répertoire de travail:
3. Importer le tableau
3. Quelle est la fonction pour visualiser les variables ?
4. Isoler "stature" dans un objet nommé taille et déterminer la nature de cette variable.
5. Calculer la moyenne, la médiane, les quartiles avec une seule fonction et l'écart-type.
6. Faire une Représentation graphique de la variable "taille".
clic pour télécharger Rstudio
C:/stat2
1.1.4. Rappel: utilisation de R
sexstat <- read.csv2("114_rappel_sexe_stature.csv")ou
Importer un fichier .csv
sexstat <- read.csv2("https://gitlab.com/formationsig/stat2/-/raw/main/donnees/114_rappel_sexe_stature.csv")
ou
> sexstat <- read.csv2("114_rappel_sexe_stature.csv"
, stringsAsFactors = T)
> str(sexstat)
$ fait : num [1:54] 2069 2070 2071 2072 2087 ...
$ sexe : Factor w/ 3 levels "F","I","M": 2 2 2 2 1 2 2 2 2 2 ...
$ stature: num [1:54] 161 NA NA NA 148 ...
> taille <- sexstat$stature
> summary(taille)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
147.6 160.2 163.8 164.5 169.7 178.0 11
> sd(taille, na.rm = TRUE)
> boxplot(taille)
> boxplot(taille~sexstat$sexe, col = c("coral", "gold", "darkturquoise"), horizontal = T)
1.1.4. Rappel: utilisation de R
Analyse et représentation graphique d'une variable quantitative
1.2. La statistique bivariée
La statistique bivariée : pourquoi ?
1
2
Résumer/décrire une grande série de donnée
en quelques chiffres ou en une figure.
Aide à la décision quant à un
possible lien entre deux variables.
Comparer deux séries de données :
égalité et discrimination
1.2 : exemple introductif
La comparaison a pour but de démontrer l'égalité de deux séries (observée/théorique), d'exclure cette égalité ou d'attester d'un lien entre elles.
L'exemple de la loterie :
module 1.2 : exemple introductif
L'exemple de la loterie :
tirage de 5 numéro parmi 49 :
La probabilité pour chaque numéro d'être tiré est identique pourtant,
les résultats réels montrent des fréquences d'apparition des numéros qui divergent
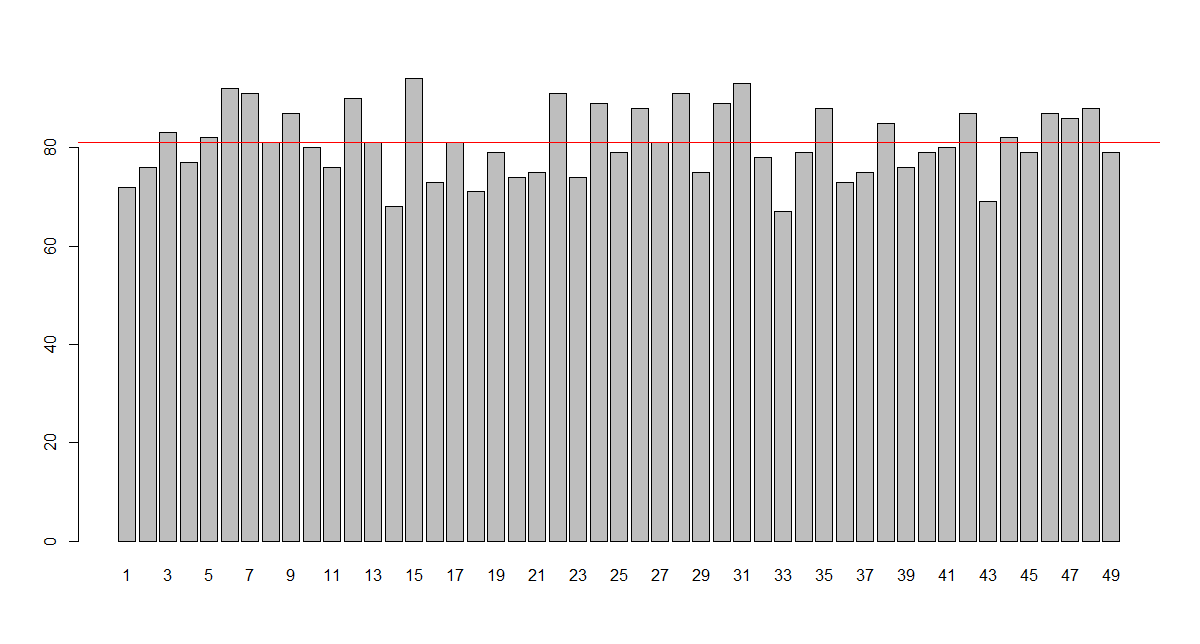
Nb de tirage = 794 soit 3970 numéro
Nb d'apparition moyen de chaque n° = 81
minimum = 67
maximum = 94
1.2 : exemple introductif
L'exemple de la loterie :
cette différence illustre les écarts d'échantillonnage (la part du hasard) que nous détaillerons ensuite et les difficultés à démontrer ou exclure des égalités
N = 3970
N = 29148
1.2. La statistique bivariée
Question de l'archéologue
La statistique bivariée : pourquoi ?
Choix du test statistique
Réalisation du test
Lire le résultat
1.2. La statistique bivariée
la nature des variables :
- 2 variables quantitatives ;
- 1 quantitative sur 2 espaces ou 2 temps distincts ;
- 1 qualitative et 1 quantitative ;
- 2 variables qualitatives.
La statistique bivariée : comment ?
1.2. L'analyse bivariée
Étape 1 : poser l'hypothèse
1.2. La statistique bivariée
1.2.2. La statistique bivariée: la procédure
1.2. L'analyse bivariée
Hypothèse nulle (H0) = premier rôle au hasard
(absence de différence)
Hypothèse alternative (H1) = différence notable
(les séries sont liées)
Il s'agit de transformer le questionnement de départ en affirmation théorique, objet du test.
L'hypothèse de travail
1.2.2. La statistique bivariée: la procédure
1.2. L'analyse bivariée
Tous les cygnes sont-ils blancs?
K. Popper (1902-1994)
1.2. La statistique bivariée
1.2.2. La statistique bivariée: la procédure
La statistique bi-variée
Tous les cygnes sont-ils blancs?
K. Popper (1902-1994)
H0 = Tous les cygnes sont blancs
H1 = Tous les cygnes ne sont pas blancs
1.2.2. La statistique bivariée: la procédure
La statistique bi-variée
Si dans notre population étudiée, il n’y a que des cygnes blancs, l’absence de preuve n’étant pas une preuve de l’absence :
il y a peut-être un cygne noir ailleurs dans le monde
1.2.2. La statistique bivariée: la procédure
La statistique bi-variée
Étape 1 : poser l'hypothèse
Formuler H0 pour qu'elle soit rejetée
1.2.2. La statistique bivariée: la procédure
La statistique bi-variée
Étape 1 : poser l'hypothèse
Formuler H0 pour qu'elle soit rejetée
Étape 2 : définir le seuil de significativité
1.2.2. La statistique bivariée: la procédure
1.2.2. La statistique bivariée: la procédure
Étape 2 : seuil de significativité
seuil de significativité (α)
degrés de liberté (ddl/df)
1.2.2. La statistique bivariée: la procédure
α est la probabilité de rejet de H0 à tort, alors que H0 est vraie
De manière conventionnelle le seuil de significativité α se situe à 95% soit 0,05 ou 99% (0,01)
Au-dessous on est dans le vert
On regarde où se place valeur calculée
au-dessus on est dans le rouge
le seuil de significativité α
La statistique bi-variée
Étape 1 : poser l'hypothèse
Formuler H0 pour qu'elle soit rejetée
Étape 2 : définir le seuil de significativité
Étape 3 : choisir le test
(variables, effectifs, distributions)
1.2.2. La statistique bivariée: la procédure
La statistique bi-variée
Étape 1 : poser l'hypothèse
Formuler H0 pour qu'elle soit rejetée
Étape 2 : définir le seuil de significativité
par exemple:
Étape 3 : choisir le test
(variables, effectifs, distributions)
Étape 4 : lire le résultat
1.2.2. La statistique bivariée: la procédure
\alpha > 0.05
1.2.2. La statistique bivariée: la procédure
le degré de liberté (ddl/df)
ddl est le nombre d'observations moins le nombre de paramètres à estimer entre ces observations.
ddl = (nbre de ligne -1) x (nbre de colonne - 1)
1.2.2. La statistique bivariée: la procédure
le p-value
ou p-valeur, "petit p", "probabilité critique"
P-value est la valeur qui "mesure l'accord entre l'hypothèse H0 et le résultat obtenu.
Plus [elle] est proche de zéro, plus forte est la contradiction [avec] H0".
Bennani Dosse M. - Statistique bivariée avec R, Rennes, PUR, 2011, p.20.
La statistique bi-variée
Étape 1 : poser l'hypothèse
Formuler H0 pour qu'elle soit rejetée
Étape 2 : définir le seuil de significativité
par exemple:
Étape 3 : choisir le test
(variables, effectifs, distributions)
Étape 4 : lire le résultat
1.2.2. La statistique bivariée: la procédure
\alpha > 0.05
Expliquer la formulation du résultat
1.2.2. La statistique bivariée: la procédure
Étape 1 : poser l'hypothèse
Formuler H0 pour qu'elle soit rejetée
Étape 2 : définir le seuil de significativité
Étape 3 : choisir le test
variable, effectif, distribution
Étape 4 : lire le résultat
p-value<α= rejet de H0
Étape 5 : interprétation
1.2.2. La statistique bivariée: la procédure
Attention : corrélation n'est pas causalité
interprétation
1.2.2. La statistique bivariée: la procédure
Attention : corrélation n'est pas causalité
interprétation
1.2.2. La statistique bivariée: la procédure
Étape 1 : poser l'hypothèse
Formuler H0 pour qu'elle soit rejetée
Étape 2 : choisir le test
variable, effectif, distribution
Étape 3 : lire le résultat
p-value<α= rejet de H0
Étape 4 : interprétation
corrélation et causalité
2. Deux variables quantitatives
2. Deux variables quantitatives
2.1 : rapport simple
Les données suivent une loi normale
Jeux de données :
- décrire chaque tableau rapidement
- quelles questions on pourrait poser à ces données?
Relation entre deux variables quantitatives
Pour notre exemple => On veut savoir si les longueurs et les largeurs des tombes sont liées
Nous pouvons commencer par estimer visuellement la corrélation avec un graphique à deux entrées
(nos deux variables)
Relation entre deux variables quantitatives
Nous pouvons commencer par estimer visuellement la corrélation avec un graphique à deux entrées
(nos deux variables)
Relation entre deux variables quantitatives
On veut savoir si les longueurs et les largeurs des tombes sont liées
commençons par regarder les variables du tableau :
#import des données
dimfos <- read.csv2("212_bavay_dim_fosse.csv", stringsAsFactors = T)
#visualisation de la structure des données
str(dimfos)
#résumé des variables longueur et largeur de fosse
summary(dimfos$long)
summary(dimfos$larg)
#graphique de la largeur de fosse en fonction de la longueur
plot(dimfos$larg~dimfos$long, pch=16, col="blue")
Relation entre deux variables quantitatives
On veut savoir si les longueurs et les largeurs des tombes sont liées
graphique de corrélation
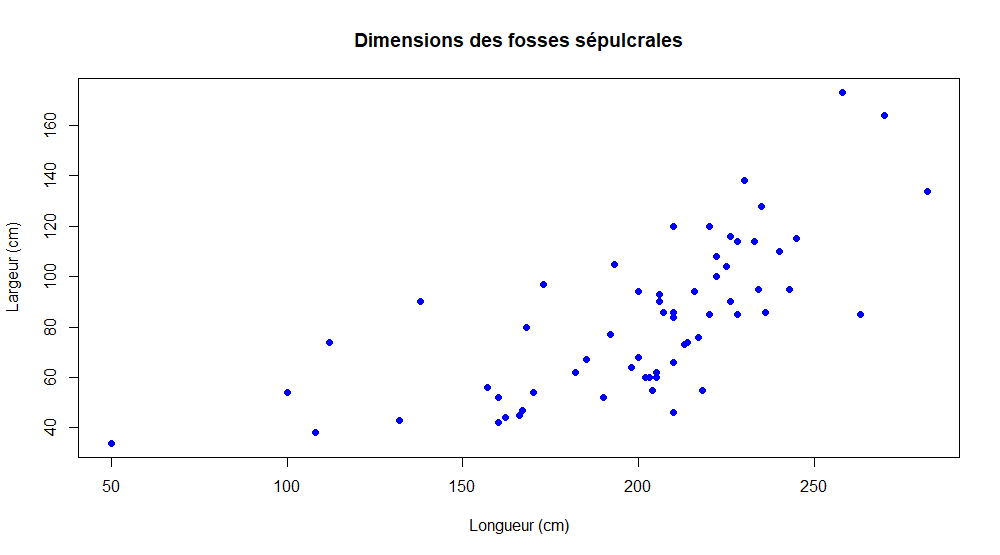
Relation entre deux variables quantitatives
Pour notre exemple => On veut savoir si les longueurs et les largeurs des tombes sont liées
On va là encore utiliser des tests d'hypothèses car les tests d’hypothèse permettent d’aider à la validation d’hypothèses.
Relation entre deux variables quantitatives
Étape 1- Poser une hypothèse
En déduire ce qu’on devrait
observer si l’hypothèse est vraie
Étape 2 - Choisir le test adapté selon si les données suivent ou non une loi normale
Étape 3 - Lire le résultat : On en conclut si on accepte ou rejette l’hypothèse initiale
Étape 4 - Interprétation
Relation entre deux variables quantitatives
"Le lien entre longueur et largeur est-il lié au hasard" ?
Relation entre deux variables quantitatives
Hypothèse nulle (H0) = premier rôle au hasard
(absence de différence)
Hypothèse alternative (H1) = différence notable
(les séries sont liées)
Il s'agit de transformer le questionnement de départ en affirmation théorique, objet du test.
L'hypothèse de travail
Relation entre deux variables quantitatives
Quand on souhaite comparer :
-
deux variables quantitatives paramétriques La distribution de la variable suit une loi normale et peut être approximée par les paramètres caractérisant une loi normale, à savoir la moyenne et la variance.
On effectuera un test paramétrique => test de Pearson
- deux variables quantitatives non paramétriques
La distribution de la variable ne ressemble pas à une distribution normale, on ne pourra pas caractériser cette distribution par des paramètres
On effectuera un test non paramétrique => test de Spearman
Relation entre deux variables quantitatives
Comment savoir si la distribution de ma variable est normale ?
Relation entre deux variables quantitatives
Comment savoir si la distribution de ma variable est normale ?
Le caractère normal de la distribution aura une influence sur le choix du test statistique. Il existe plusieurs méthodes pour déterminer si la distribution est normale
-
1ère méthode graphique : l’histogramme
-
2ème méthode graphique : le diagramme Quantile-Quantile
-
une méthode statistique : le test de Shapiro-Wilk
Relation entre deux variables quantitatives
Comment savoir si la distribution de ma variable est normale ?
Limites de ces méthodes
Ces 3 méthodes ont leurs limites, il faut les interpréter avec précaution :
Les méthodes graphiques ne permettent pas de trancher de manière objective sur la normalité de la distribution. On regarde à l’œil nu si la distribution suit à peu près une loi normale, on décide de manière subjective
La méthode statistique permet de trancher mais avec les risques d’erreur inhérents à tout test statistique. Ainsi, si p > alpha, on ne rejette pas H0 mais on ne peut pas l’accepter pour autant. C’est d’autant plus vrai que l’échantillon est faible car la puissance le sera aussi.
Il n’y a pas de critère absolu. Dans le doute, pour un cas intermédiaire, le mieux est de pratiquer les deux types de tests (paramétrique et non paramétrique) et de comparer les résultats.
Relation entre deux variables quantitatives
α est la probabilité de rejet de H0 à tort, alors que H0 est vraie
De manière conventionnelle le seuil de significativité α se situe à 95% soit 0,05 ou 99% (0,01)
Au-dessous on est dans le vert
On regarde où se place valeur calculée
au-dessus on est dans le rouge
le seuil de significativité α
Relation entre deux variables quantitatives
le p-value
ou p-valeur, "petit p", "probabilité critique"
P-value est la valeur qui "mesure l'accord entre l'hypothèse H0 et le résultat obtenu.
Plus [elle] est proche de zéro, plus forte est la contradiction [avec] H0".
Bennani Dosse M. - Statistique bivariée avec R, Rennes, PUR, 2011, p.20.
Relation entre deux variables quantitatives
Exercice : corrélation entre longueur et largeur des fosses sépulcrales de Bavay
Graphique a double entrée :
plot(bavay$long,bavay$larg)Relation entre deux variables quantitatives
Exercice : corrélation entre longueur et largeur des fosses sépulcrales de Bavay
Calcul de la droite de régression :
p-value = 3.221e-12
rho = 0.7467021
lm(bavay$larg~bavay$long) reg1<-lm(bavay$long~bavay$larg) plot(bavay$larg,bavay$long) abline(reg1,col=”red”)
Relation entre deux variables quantitatives
Exercice : corrélation entre longueur et largeur des fosses sépulcrales de Bavay
Calcul de la droite de régression : ce n'est pas une droite !
Un autre facteur peut expliquer
cette double droite
library(car) scatterplot(long~larg, data=bavay)
Relation entre deux variables quantitatives
Exercice : corrélation entre longueur et largeur des fosses sépulcrales de Bavay
plot(bavay$long, bavay$larg, pch=18, col=c("blue","orange","green")[bavay$age_simpl]) legend("topleft", legend =c("NA","Adulte","Immature"), fill=c("blue","orange","green"))
Séparons les individus par âge :
deux groupes se séparent
Relation entre deux variables quantitatives
immat <- subset(bavay, age_simpl=="immature") adulte <- subset(bavay, age_simpl=="adulte") reg2 <- lm(immat$larg~immat$long) abline(reg2, col="green") reg3 <- lm(adulte$larg~adulte$long) abline(reg3, col="orange")
Refaisons la corrélation par âge
immatures :
p-value = 0.05021
cor = 0.5319941
adultes :
p-value = 1.462e-10
rho = 0.7814843
meilleure corrélation adulte
moins bonne
p-value
2.2 Plusieurs variables quantitatives: lire une ACP
Lire une ACP (analyse en composante principale) :
L'exemple des notes d'élèves dans quatre disciplines
Relation entre deux variables quantitatives
Interro surprise :
ouvrez le fichier "exo_TP_Pompéi.csv" et déterminez s'il y a un lien significatif entre le diamètre et la profondeur des poteaux
1 3. variable quantitative/2 espaces ou périodes
Quand on souhaite comparer :
-
une même variable quantitative sur deux sites différents (exemple, les volumes des silos du site A vs ceux du site B) ;
-
une même variable quantitative pour deux périodes chronologiques distinctes (exemple, les volumes des silos de la phase 1 vs ceux de la phase 2) ;
-
une même variable quantitative par rapport à une seconde variable qualitative à deux modalités (exemple, les volumes des silos piriformes vs ceux des coniques) ;
-
un échantillon par rapport à une population donnée via une même variable quant. (exemple, les volumes des silos du secteur 1 vs ceux du reste du site),
On utilise un grand classique des statistiques : le test t de Student
qui s’intéresse aux moyennes de chaque série.
1 3. variable quantitative/2 espaces ou périodes
William S. Gosset (1876-1937)
alias Student
1 3. variable quantitative/2 espaces ou périodes
1 3. variable quantitative/2 espaces ou périodes
Le test t de Student
Étape 1 : poser l'hypothèse
H0 : La différence d'altitude des fosses sépulcrales
entre les phases 3 et 4 est due au hasard.
1 3. variable quantitative/2 espaces ou périodes
variable quantitatives/2 espaces ou périodes
Le test t de Student
Étape 1 : poser l'hypothèse
H0 : il n'y a pas de différence statistiquement significative entre les altitudes des fonds de fosses sépulcrales des tombes des phases chronologiques 3 et 4.
Étape 2 : choisir le test
2 conditions de validité :
- les deux séries se distribuent selon la loi normale
- les deux variances sont égales (homoscédastique)
1 3. variable quantitative/2 espaces ou périodes
Le test f de Fisher
Étape 1 : poser l'hypothèse
H0 : la différence entre les variances est due au hasard
Étape 2 : choisir le test
une condition de validité :
- les deux distributions d'alti inf suivent la loi normale
var.test(alti$z_inf[alti$phase==3],alti$z_inf[alti$phase==4])1 3. variable quantitative/2 espaces ou périodes
Le test f de Fisher
Étape 3 : lire le résultat
On ne peut pas rejeter H0
Il est acceptable de considérer les variances comme égales
Étape 1 : poser l'hypothèse
H0 : la différence entre les variances est due au hasard
Étape 2 : choisir le test
une condition de validité :
- les deux distributions d'alti inf suivent la loi normale
1 3. variable quantitative/2 espaces ou périodes
var.test(alti$z_inf[alti$phase==3],alti$z_inf[alti$phase==4])Le test f de Fisher
Étape 1 : poser l'hypothèse
H0 : la différence entre les variances est due au hasard
Étape 2 : choisir le test
une condition de validité :
- les deux distributions d'alti inf suivent la loi normale
Étape 3 : lire le résultat
On ne peut pas rejeter H0
Il est acceptable de considérer les variances comme égales
Étape 4 : Interprétation
1 3. variable quantitative/2 espaces ou périodes
var.test(alti$z_inf[alti$phase==3],alti$z_inf[alti$phase==4])Le test t de Student
1 3. variable quantitative/2 espaces ou périodes
Le test t de Student
Commandes R :
- Condition 1: loi normale :
- Condition 2: égalité des variances :
- Tests : si 2 conditions remplies:
si condition 1 non remplie :
hist(alti$z_inf[alti$phase==3]) ggpubr::ggqqplot(alti$z_inf[alti$phase==3]) shapiro.test(alti$z_inf[alti$phase==3])
var.test(alti$z_inf[alti$phase==3],
alti$z_inf[alti$phase==4])1 3. variable quantitative/2 espaces ou périodes
t.test(alti$z_inf[alti$phase==3],alti$z_inf[alti$phase==4],var.equal = TRUE)wilcox.test(alti$z_inf[alti$phase==2],alti$z_inf[alti$phase==5]3.5. Relation entre 1 variable qual. et 1 variable quant.
anova : c'est l'analyse de la variance
3.5. Relation entre 1 variable qual. et 1 variable quant.
La variance c'est « La moyenne de la somme des carrés des écarts par rapport à la moyenne arithmétique. »
-
Calculer la moyenne.
-
Calculer pour chaque modalité, son écart à la moyenne (parfois les écarts seront positifs parfois négatifs).
-
Mettre ces écarts au carré (pour qu'ils soient tous positifs et pour accentuer les écarts-importants).
-
Faire la somme de ces écarts au carré.
-
C'est une moyenne, il faut donc diviser le tout par l'effectif.
-
→ Bravo vous avez calculé la Variance !
3.5. Relation entre 1 variable qual. et 1 variable quant.
ANOVA : dépendance des variables
L'ANOVA permet de tester la dépendance d'une variable quantitative à une variable qualitative
3.5. Relation entre 1 variable qual. et 1 variable quant.
L'ANOVA permet de tester la dépendance d'une variable quantitative à une variable qualitative
> Variable qualitative = facteur (expliquant la dépendance)
> ANOVA à 1 seul facteur : analyse bivariée
> ANOVA à 2 facteurs : analyse multivariée
ANOVA : dépendance des variables
3.5. Relation entre 1 variable qual. et 1 variable quant.
Question : La dépendance des séries étudiées est-elle significative pour le facteur considéré?
ANOVA : dépendance des variables
3.5. Relation entre 1 variable qual. et 1 variable quant.
Question : La dépendance des séries étudiées est-elle significative pour le facteur considéré?
Pour répondre à cette question, l'ANOVA va comparer les moyennes des séries et tester leur variance (par un test de Fisher).
ANOVA : dépendance des variables
3.5. Relation entre 1 variable qual. et 1 variable quant.
Question : La dépendance des séries étudiées est-elle significative pour le facteur considéré?
Hypothèse nulle (H0) = égalité des moyennes
(donc non dépendance)
Hypothèse alternative (H1) = 1 moyenne au moins s'écarte
(donc dépendance)
ANOVA : dépendance des variables
3.5. Relation entre 1 variable qual. et 1 variable quant.
1. Ouvrir Rstudio
2. Ouvrir un nouveau script
3. L'enregistrer en script_anova.R
4. Renommer le tableau bilansoc
5. On regarde la structure de notre tableau
ANOVA : dépendance des variables
3.5. Relation entre 1 variable qual. et 1 variable quant.
Question : La dépendance entre le sexe et le salaire à l'Inrap est-elle significative?
Hypothèse nulle (H0) = ?
Hypothèse alternative (H1) = ?
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
Question : La dépendance entre le sexe et le salaire à l'Inrap est-elle significative ?
Hypothèse nulle (H0) = non il n'y a pas de lien de dépendance entre sexe et salaire (égalité des moyennes)
Hypothèse alternative (H1) = oui il existe au moins une distribution dont la moyenne s'écarte des autres
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
6. on fait une boîte à moustache pour visualiser notre question : le sexe a-t-il une influence sur le salaire ?
boxplot(bilansoc$salaire~bilansoc$sexe)
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
On reprend le tableau, on réimporte,
renomme : bilansoc2
visualise la structure...
Nouveau boxplot, qu'on peut rendre un peu plus joli
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
On reprend le tableau
On réimporte
On renomme : bilansoc2
On visualise la structure...
Nouveau boxplot, qu'on peut rendre un peu plus joli
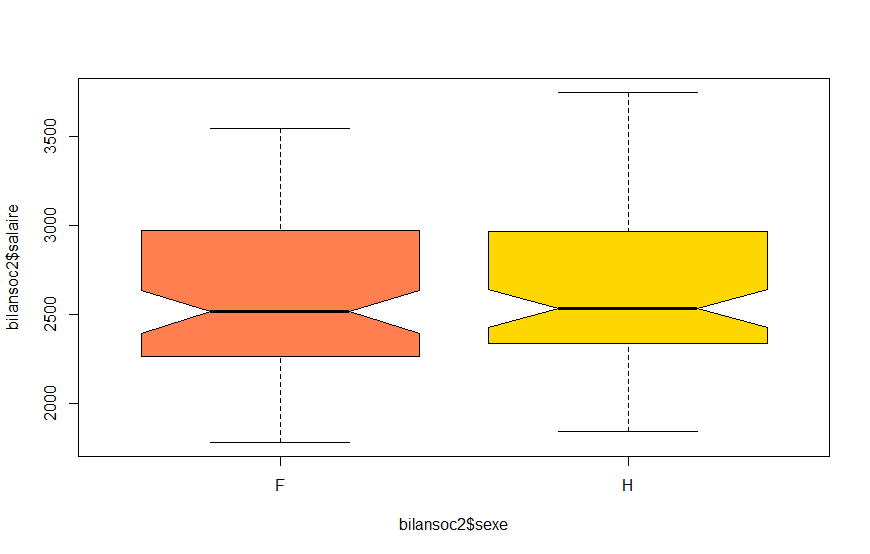
boxplot(bilansoc2$salaire~bilansoc2$sexe , notch=TRUE
, col=c("coral","gold"))ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
Les salaires des femmes et hommes ne semblent pas différents (pas de dépendance).
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
Pour cela nous allons faire une analyse de la variance (tester l'égalité des moyennes)
ANOVA
ANalysis Of VAriance
ANOVA : dépendance des variables
Question : La dépendance entre le sexe et le salaire à l'Inrap est-elle significative ?
4. Relation entre 1 variable qual. et 1 variable quant.
Question : La dépendance entre le sexe et le salaire à l'Inrap est-elle significative ?
ANOVA : dépendance des variables
Hypothèse nulle (H0) = non il n'y a pas de lien de dépendance entre sexe et salaire (égalité des moyennes)
Hypothèse alternative (H1) = oui il existe au moins une distribution dont la moyenne s'écarte des autres
4. Relation entre 1 variable qual. et 1 variable quant.
ANOVA : dépendance des variables
aov(bilansoc2$salaire~bilansoc2$sexe)Question : La dépendance entre le sexe et le salaire à l'Inrap est-elle significative ?
4. Relation entre 1 variable qual. et 1 variable quant.
ANOVA : dépendance des variables
ANOVA : dépendance des variables
bilansoc2$sexe Residuals
Sum of Squares 336265 44571213
Deg. of Freedom 1 172
Residual standard error: 509.053
Question : La dépendance entre le sexe et le salaire à l'Inrap est-elle significative ?
4. Relation entre 1 variable qual. et 1 variable quant.
aov(bilansoc2$salaire~bilansoc2$sexe)Pour avoir le résultat du test, il nous faut le Pvalue, pour cela on va d'abord renommer notre analyse avant de faire summary
ANOVA : dépendance des variables
Question : La dépendance entre le sexe et le salaire à l'Inrap est-elle significative ?
4. Relation entre 1 variable qual. et 1 variable quant.
bilansoc2$sexe Residuals
Sum of Squares 336265 44571213
Deg. of Freedom 1 172
Residual standard error: 509.053
aov(bilansoc2$salaire~bilansoc2$sexe)anova<-aov(bilansoc2$salaire~bilansoc2$sexe)
summary(anova)4 une variable qualitative et une quantitative : ANOVA
moyenne
des carrés
somme
des carrés
test de
Fisher
P value
degrés de liberté
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
moyenne
des carrés
somme
des carrés
test de
Fischer
P value
degrés de liberté
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
Cela signifie qu’elle permet d’identifier une différence ou pas...
mais ne dit pas quels groupes spécifiques sont statistiquement
différents les uns des autres
moyenne
des carrés
somme
des carrés
test de
Fischer
P value
degrés de liberté
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
Exercice
A vous de jouer !
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
anova2 <- donnees_exo_anova2
str(anova2)
boxplot(anova2$poids~anova2$magnetisme
,horizontal = T)
summary(aov(anova2$poids~anova2$magnetisme))ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
Y a-t-il un lien entre le magnétisme et le poids des culots?
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
anova2 <- donnees_exo_anova2
str(anova2)
boxplot(anova2$poids~anova2$magnetisme
,horizontal = T)
summary(aov(anova2$poids~anova2$magnetisme))> anova2=donnees_exo_anova2
> str(anova2)
> boxplot(anova2$poids~anova2$magnetisme,horizontal = T)
> summary(aov(anova2$poids~anova2$magnetisme))
ANOVA : dépendance des variables
4. Relation entre 1 variable qual. et 1 variable quant.
Qu'est-ce qu'une variable qualitative ?
4. Relation entre deux variables qualitatives
Rappel : comment étudie t-on une variable qualitative ?
Relation entre deux variables qualitatives
Catégories fonctionnelles de céramique
Rappel : comment étudie t-on une variable qualitative ?
Relation entre deux variables qualitatives
Tableau de dénombrement :
246 !
Rappel : comment étudie t-on une variable qualitative ?
Relation entre deux variables qualitatives
Tableau de dénombrement :
Fréquence absolue (NMI)
table(ceram$Fonction)
Fréquence relative (%)
table(ceram$Fonction)/length(ceram$Fonction)*100
Rappel : comment étudie t-on une variable qualitative ?
Relation entre deux variables qualitatives
Tableau de dénombrement :
Représentation graphique :
Fréquence absolue (NMI)
Fréquence relative (%)
Tester le lien entre deux variables qualitatives :
le khi²
Relation entre deux variables qualitatives
Tester le lien entre deux variables qualitatives :
le khi²
Relation entre deux variables qualitatives
un moustachu
Tester le lien entre deux variables qualitatives : le khi²
Relation entre deux variables qualitatives
Proposé par Karl Pearson en 1900 dans l'article :
Sur le critère de décider si, dans le cas d'un système de variables en corrélation, un ensemble donné de déviations par rapport à la valeur probable est tel qu'il peut être raisonnablement supposé avoir été obtenu par un échantillonnage au hasard.
dans Phylosophical Magazine
Relation entre deux variables qualitatives
Pour étudier la relation entre 2 variables qualitatives,
la démarche est toujours identique :
1- Formuler une hypothèse
2- En déduire ce qu’on devrait observer si l’hypothèse est vrai
3- Choisir le test adapté
4- On en conclut si on accepte ou rejette l’hypothèse initiale
Relation entre deux variables qualitatives
1er exemple : sexe / catégorie professionnelle
Le jeu de données est tiré du bilan social de l'Inrap (2018) duquel ont été extraites deux variables : le sexe et la catégorie des agents
Relation entre deux variables qualitatives
Hypothèses :
Que cherche t-on à voir à partir de ces deux variables ?
Relation entre deux variables qualitatives
Hypothèses :
Que cherche t-on à voir à partir de ces deux variables ?
Si un lien existe entre le sexe et la catégorie
=
si ce lien est suffisamment marqué pour exclure qu’il s’agisse simplement de variations liées au hasard
Relation entre deux variables qualitatives
Hypothèses :
Que cherche t-on à voir à partir de ces deux variables ?
Est-ce que le sexe d'un agent a une influence sur sa catégorie professionnelle (l'inverse n'étant pas possible) ?
H0: NON, les différences de catégories salariales entre hommes et femmes peuvent être dues au hasard
H1 : OUI, la catégorie salariale est liée à l’identité sexuelle des agents
Relation entre deux variables qualitatives
Comment fait-on pour mettre en évidence l'interaction ?
Un tableau de dénombrement !
Relation entre deux variables qualitatives
Comment fait-on pour mettre en évidence l'interaction ?
Il nous faut une référence, un cas parfait auquel comparer notre échantillon
Relation entre deux variables qualitatives
Comment fait-on pour mettre en évidence l'interaction ?
Il nous faut une référence, un cas parfait auquel comparer notre échantillon
Ca n'existe pas, il faut le créer, il sera théorique
Relation entre deux variables qualitatives
Cette valeur théorique est :
Par exemple, pour les femmes de catégorie 2 :
S'il n'y a pas de lien entre sexe est catégorie, la probabilité d'être une femme de catégorie 2 est égale à la probabilité d'être une femme (à l'Inrap) x la probabilité d'avoir un poste de catégorie 2 soit :
Σligne×Σcolonne / Σtotal
Relation entre deux variables qualitatives
A partir de ce tableau de référence, nous pouvons calculer les écarts à l'indépendance pour chaque paire de variable
Effectif observé - Effectif théorique
(n-n')
Cela renvoie à la matrice de variance co-variance pour les données quantitatives
Relation entre deux variables qualitatives
A partir de ce tableau il est possible de calculer la valeur du Khi² :
la somme de carrés des écarts observé/théorique sur l'effectif théorique par couple de variable
χ2= Σ(Effectif observé - Effectif théorique)²/
Effectif théorique
C'est un calcul de variance !
Relation entre deux variables qualitatives
On compare avec la table du khi² :
Le degré de liberté :
en simplifiant, c'est le nombre d'autres possibilités offertes à un individu
Pour le X² = nb de colonne-1
x nb ligne-1
Relation entre deux variables qualitatives
On compare avec la table du khi² :
6,54 < 7,81 donc
avec une probabilité de 95 % la distribution des catégories par sexe
à l'Inrap peut être expliquée par des variations d'échantillonnage (au recrutement) liées au hasard
On ne rejette pas H0, on ne peut pas conclure !
Relation entre deux variables qualitatives
Le même exercice avec R :
#j'importe le tableau des sexes et catégories à l'Inrap #dans un objet nommé catsex inrap <- read.csv2("420_cat_sex.csv",stringsAsFactors = T) #je regarde la structure du tableau str(inrap)
Relation entre deux variables qualitatives
Le même exercice avec R :
#je transforme la variable catégorie en facteur inrap$categorie <- as.factor(inrap$categorie) #tableau de contigence table(inrap$sexe,inrap$categorie)
Relation entre deux variables qualitatives
Le même exercice avec R :
#les conditions du test du khi² sont remplies (effectif > ou = à 5 pour # chaque combinaison de variable) #je lance le test et le stock dans l'objet res res <- chisq.test(inrap$sexe,inrap$categorie) #je peux voir le tableau de contingence observé res$observed
Relation entre deux variables qualitatives
Le même exercice avec R :
#je peux voir le tableau de contingence esperé res$expected
#et enfin le résultat du test res
Relation entre deux variables qualitatives
Le même exercice avec R :
#je fais un diagramme en ballon #je charge la librairie gplots library(gplots) #je fais un diagramme en ballon balloonplot(table(inrap$sexe,inrap$categorie))
#et enfin le résultat du test res
Relation entre deux variables qualitatives
Les pré-requis du khi² :
-
Il faut avoir un effectif minimum de 5 pour chacune des combinaisons de variable (dans chaque case du tableau de contingence)
-
pour les très petits tableaux de contingence (2 lignes, 2 colonnes, une correction dite de Yates est nécessaire, R le fait tout seul, il s'agit de retrancher 0,5 à la différence observé/théorique)
Relation entre deux variables qualitatives
Les pré-requis du khi² :
-
Il faut avoir un effectif minimum de 5 pour chacune des combinaisons de variable (dans chaque case du tableau de contingence)
Si au moins une des combinaisons de variable
a un effectif inférieur à 5 :
Relation entre deux variables qualitatives
Les post-requis du khi² :
Si au moins une des combinaisons de variable
a un effectif inférieur à 5 :
test exact de Fisher :
fisher.test(variable1,variable2)
Relation entre deux variables qualitatives
Les différents test du khi² :
- Test du χ2 d'indépendance :
permet d'évaluer le lien entre deux variables
- Test du χ2 d'adéquation :
permet d'évaluer la correspondance entre un échantillon et une distribution de référence (par exemple le sex-ratio)
! le choix de cette référence est primordiale
- Test du χ2 d'homogénéité :
compare deux échantillons de même effectif
Relation entre deux variables qualitatives
C'est à vous !
A partir du fichier ceram_categorie_fonction.csv
- Regarder les données
- formuler les hypothèses
- faire un test
Relation entre deux variables qualitatives
Pour aller plus loin : l'AFC
exemple d'utilisation en ligne :
http://analyse.univ-paris1.fr/
on importe le tableau de contingence
Relation entre deux variables qualitatives
AFC : le graphique
Relation entre deux variables qualitatives
CAH: le graphique
Stat "a la carte" 2.1
By Formation_SIG
