QCross: Quantum
Cross-Platform Testing
Supervisors:
Dr. Shaukat Ali and Dr. Christoph Laaber
Simula Research Laboratory
Applying differential and metamorphic testing techniques to test IBM Qiskit, Rigetti PyQuil, and Google Cirq

About me
Arfat Salman
Master in Informatics: Programming and System Architecture

Arrange
Assert
Act
Arrange
Assert
Act
Quantum Computer
Uses quantum physics concepts like superposition and entanglement to achieve computation

IBM Quantum scientist Dr. Maika Takita in lab
Proposed in the 1980s by Richard Feynman and Yuri Manin
A new kind of computing machine
*Not a replacement for classical computer
Why?
Due to their unique computational paradigm, quantum computers can solve certain problems exponentially faster and more efficiently than their classical counterparts.
Examples
- Shor's Algorithm: Factors an integer N in polylogarithmic time.
- Deutsch–Jozsa algorithm: determines whether a binary function is constant or balanced (returning equal numbers of 0s and 1s) one single operation
Why?
Deutsch–Jozsa algorithm
def balanced_fn(n_bit_arg):
if some_condition(n_bit_arg):
return 0
return 1
balanced_fn('001') # => 1
balanced_fn('011') # => 0
balanced_fn('010') # => 0balanced: Half of inputs return 1, other half 0
constant: 0 or 1 on all inputs
Classical Computer:
Quantum Computer:
We shouldn’t be asking ‘where do quantum speedups come from?’ we should say ‘all computers are quantum, [...]’ and ask ’where do classical slowdowns come from?’
How?
https://quantum.country/
Qubit
Quantum Bit
Qubit
Quantum Bit
dead
alive
Qubit
Quantum Bit
dead
alive
Qubit
Quantum Bit
dead
alive
Ket
Qubit
Quantum Bit
Superposition
dead
alive
Qubit
Quantum Bit
Superposition
dead
alive
Qubit
Quantum Bit
Superposition
dead
alive
Qubit
Quantum Bit
Superposition
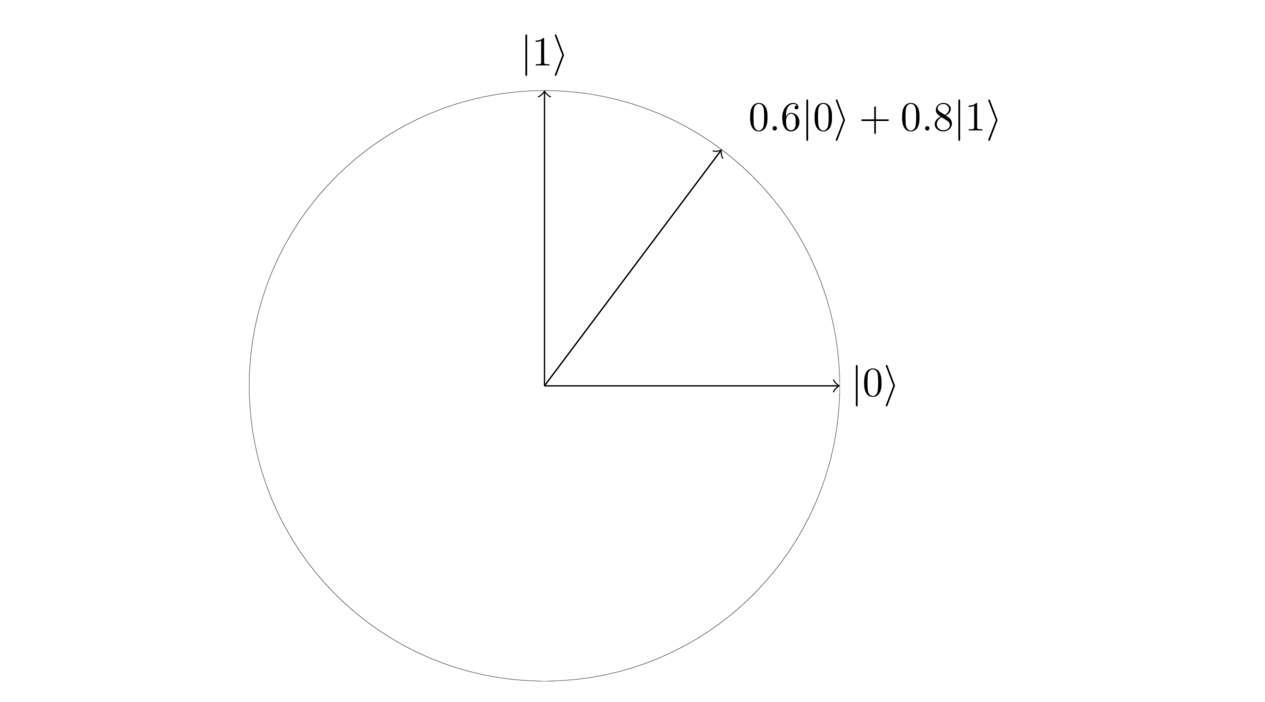
dead
alive
Qubit
Quantum Bit
Superposition
probability of observing a 0
probability of observing a 1
Schrödinger's cat
dead
alive
Quantum Gate
A quantum gate is a unitary matrix that acts on a quantum state and changes it.
Qubit
Flipped Probailities
Other quantum gates
Hadamard Gate (H):
Single qubit gate that puts a quantum state in superposition
Controlled-NOT gate:
Two-qubit quantum gate
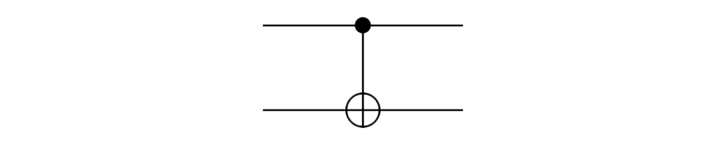
Other quantum gates
Hadamard Gate (H):
Single qubit gate that puts a quantum state in superposition
Controlled-NOT gate:
Two-qubit quantum gate

Other quantum gates
Hadamard Gate (H):
Single qubit gate that puts a quantum state in superposition
Controlled-NOT gate:
Two-qubit quantum gate

Quantum Computation
Quantum computation is a change in the quantum state (i.e., the state of a qubit, the quantum bit).
- A pure quantum computation is reversible. (applying the reverse of the gate will inverse the operation)
- A quantum state cannot be copied due to No-cloning theorem (most assignment operations become impossible)
- Intermediate quantum state cannot be read as it leads to collapse of quantum state (no debugging or print statements)
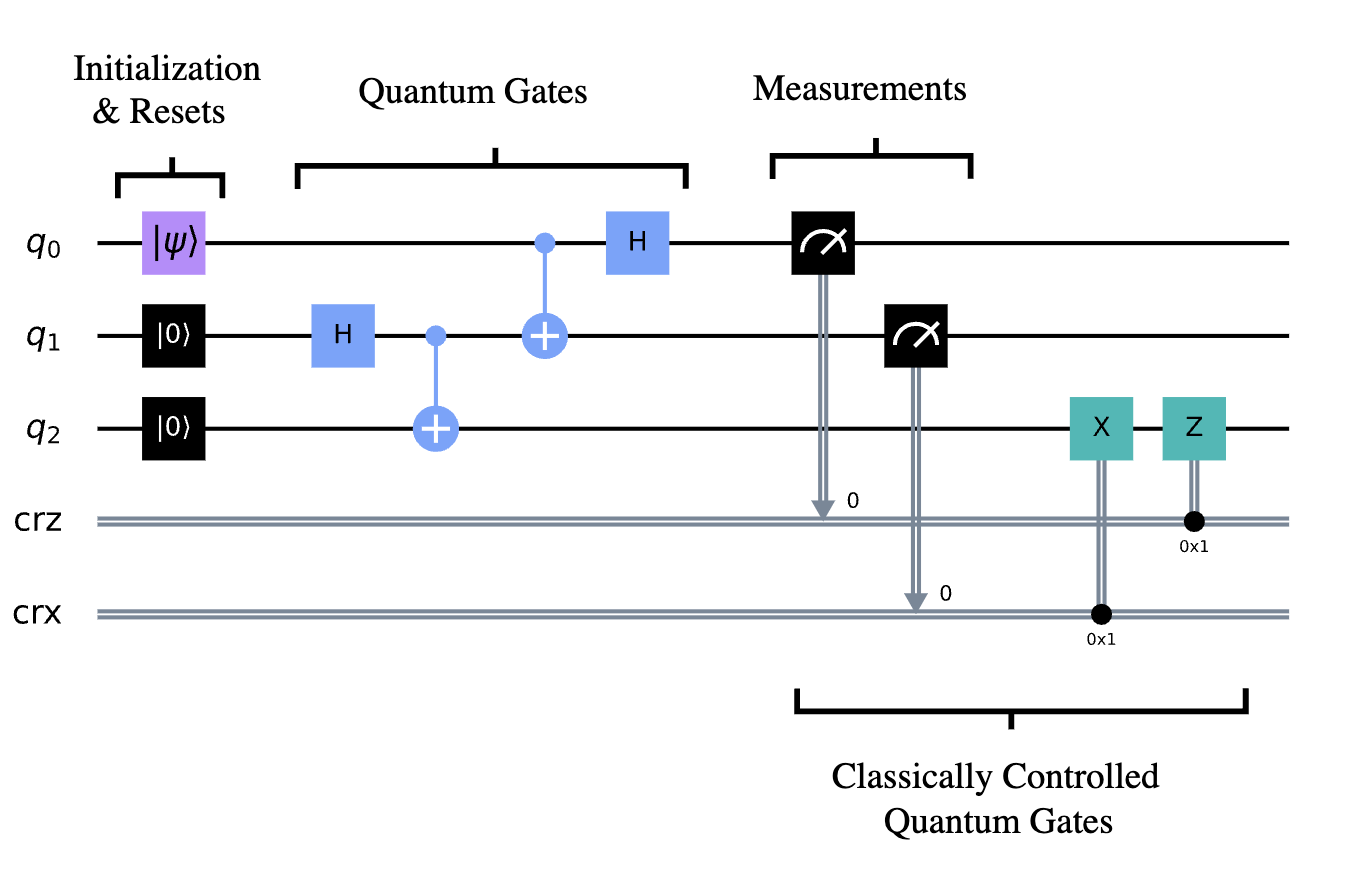
Quantum Circuit
QSP
Quantum Software Platforms
https://thequantuminsider.com/2022/09/05/quantum-computing-companies-ultimate-list-for2022/
Standalone or embedded quantum programming language or API
Quantum simulator that emulates instructions on a classical device
Optimizing compiler that translates high-level language into quantum gate instructions
Software controller that sends analog signals to quantum hardware

pyQuil

Cirq
Bugs in QSPs
Microsoft Q#
Google Cirq
Rigetti PyQuil
IBM Qiskit
% of bug-labelled GitHub issues
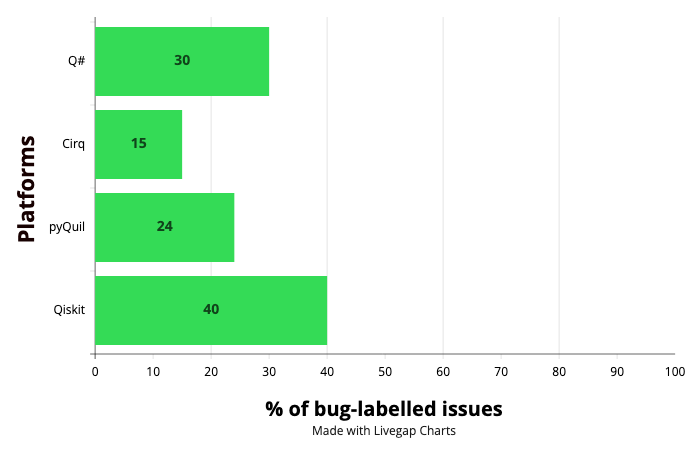
Bugs in QSPs

Microsoft Q#
Google Cirq
Rigetti PyQuil
IBM Qiskit
% of bug-labelled GitHub issues
30
15
24
40
😵
Challenges in Testing QSPs
C1: The need for a significant quantity of quantum test programs.
C2: Cross-platform testing is hard due to varying support and APIs, needing manual porting.
C3: Presence of stochasticity.
Lack of generalised automated testing techniques within quantum settings
Testing Overview
Quantum Software Testing (and testing at large) is facing two fundamental problems:
Oracle Problem
The Reliable Test-Set problem
Testing Overview
Quantum Software Testing (and testing at large) is facing two fundamental problems:
Oracle Problem
The Reliable Test-Set problem
situations where it is extremely difficult, or impossible, to verify the test result of a given test case
the challenge of creating a set of tests that can adequately and accurately assess the functionality and performance of a software system.
Differential Testing
This technique involves supplying identical input to comparable applications or distinct implementations of the same application and observing discrepancies in their performance and behaviour.
Solves the Oracle Problem
Python
Source
CPython
PyPy
Same Result
Differential Testing
This technique involves supplying identical input to comparable applications or distinct implementations of the same application and observing discrepancies in their performance and behaviour.
Solves the Oracle Problem
Quantum
Algorithm
Qiskit
Cirq
Same Result
after necessary translations
Metamorphic Testing
property-based software testing technique
Metamorphic Testing
property-based software testing technique
Algorithm
passing
test case
Metamorphic Testing
property-based software testing technique
Algorithm
new test case
using algorithm property
passing
test case
Metamorphic Testing
property-based software testing technique
Algorithm
new test case
using algorithm property
Same Result
passing
test case
Metamorphic Testing
property-based software testing technique
min
min(4,5)
min(5,4)
swapping arguments order does not change answer
Same Result
Algorithm
passing
test case
new test case
using algorithm property
Same Result
Metamorphic Testing
property-based software testing technique
min
min(4,5)
min(5,4)
swapping arguments order does not change answer
Same Result
Algorithm
passing
test case
new test case
using algorithm property
Same Result
Source
Follow-up
Prior Work
QDiff
MorphQ
- 6 hand-written quantum programs
- Evaluated on 3 platforms( Qiskit, Cirq, PyQuil) and quantum hardware
- Uses mutation testing to create increased program divergence
- Generates random Qiskit quantum programs
- Establishes 10 metamorphic relations
-
Uses metamorphic testing to test
- Only Qiskit
Contribution of the thesis
- Used MorphQ to generate random Qiskit Programs
- Provide basis for translating metamorphic relations in Cirq and PyQuil.
- Built a MR-aware quantum program translator that translates MorphQ Qiskit programs to Cirq and PyQuil programs.
- As part of translation, created a cross-platform quantum gate library (bloqs)
Research Questions
-
RQ1: How many syntactically different but correct programs can be translated by QCross’s converter?
-
RQ2: What has QCross found via cross-platform testing of the widely-used QSSes? i.e., how many warnings and errors do QCross produce?
-
RQ3: How does QCross compare to prior work on testing quantum computing platforms?
- RQ4: How useful is Bloqs?
QCross's Program Translation Process
Each quantum program can be logically divided into six parts:
- import statements
- Declaration of circuits / qubits / classical bits
- Application of gates and addition of terminal measurements
- Preparation of the circuit to be executed on simulators / optimiziations
- Execution of the program
- Collection of the results
qr = QuantumRegister(7, name='qr')
cr = ClassicalRegister(7, name='cr')
qc = QuantumCircuit(qr, cr, name='qc')qc = cirq.Circuit()
qr = [cirq.NamedQubit('q' + str(i)) for i in range(7)]qc = Program()
cr = qc.declare("ro", "BIT", 7)Declarations
Cirq
Qiskit
PyQuil
qr = QuantumRegister(7, name='qr')
cr = ClassicalRegister(7, name='cr')
qc = QuantumCircuit(qr, cr, name='qc')qc = cirq.Circuit()
qr = [cirq.NamedQubit('q' + str(i)) for i in range(7)]qc = Program()
cr = qc.declare("ro", "BIT", 7)Declarations (Circuit)
Cirq
Qiskit
PyQuil
qr = QuantumRegister(7, name='qr')
cr = ClassicalRegister(7, name='cr')
qc = QuantumCircuit(qr, cr, name='qc')qc = cirq.Circuit()
qr = [cirq.NamedQubit('q' + str(i)) for i in range(7)]qc = Program()
cr = qc.declare("ro", "BIT", 7)Declarations (Quantum Register)
Cirq
Qiskit
PyQuil
qr = QuantumRegister(7, name='qr')
cr = ClassicalRegister(7, name='cr')
qc = QuantumCircuit(qr, cr, name='qc')qc = cirq.Circuit()
qr = [cirq.NamedQubit('q' + str(i)) for i in range(7)]qc = Program()
cr = qc.declare("ro", "BIT", 7)Declarations (Classical Register)
Cirq
Qiskit
PyQuil
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
qr = QuantumRegister(7, name='qr')
cr = ClassicalRegister(7, name='cr')
qc = QuantumCircuit(qr, cr, name='qc')import cirq
qc = cirq.Circuit()
qr = [cirq.NamedQubit('q' + str(i)) for i in range(7)]from pyquil import Program
qc = Program()
cr = qc.declare("ro", "BIT", 7)Import statements
Cirq
Qiskit
PyQuil
Application of gates
from qiskit.circuit.library.standard_gates import *
qc.append(ZGate(), qargs=[qr[2]], cargs=[])
qc.append(CHGate(), qargs=[qr[2], qr[0]], cargs=[])
qc.append(RYYGate(5.398622178940033), qargs=[qr[0], qr[2]], cargs=[])import cirq
qc.append(cirq.Z( qr[2] ))from pyquil.gates import *
qc.inst(Z(2))Cirq
Qiskit
PyQuil
Application of gates
from qiskit.circuit.library.standard_gates import *
qc.append(ZGate(), qargs=[qr[2]], cargs=[])
qc.append(CHGate(), qargs=[qr[2], qr[0]], cargs=[])
qc.append(RYYGate(5.398622178940033), qargs=[qr[0], qr[2]], cargs=[])import cirq
qc.append(cirq.Z( qr[2] ))from pyquil.gates import *
qc.inst(Z(2))Cirq
Qiskit
PyQuil
Application of gates
from qiskit.circuit.library.standard_gates import *
qc.append(ZGate(), qargs=[qr[2]], cargs=[])
qc.append(CHGate(), qargs=[qr[2], qr[0]], cargs=[])
qc.append(RYYGate(5.398622178940033), qargs=[qr[0], qr[2]], cargs=[])import cirq
qc.append(cirq.Z( qr[2] ))
qc.append(cirq.H.controlled()( qr[2], qr[0] ))from pyquil.gates import *
qc.inst(Z(2))
# control qubit 2 and target qubit 0
qc.inst(H(0).controlled(2))Cirq
Qiskit
PyQuil
Application of gates
from qiskit.circuit.library.standard_gates import *
qc.append(ZGate(), qargs=[qr[2]], cargs=[])
qc.append(CHGate(), qargs=[qr[2], qr[0]], cargs=[])
qc.append(RYYGate(5.398622178940033), qargs=[qr[0], qr[2]], cargs=[])import cirq
qc.append(cirq.Z( qr[2] ))
qc.append(cirq.H.controlled()( qr[2], qr[0] ))
# ??from pyquil.gates import *
qc.inst(Z(2))
# control qubit 2 and target qubit 0
qc.inst(H(0).controlled(2))
# ??Cirq
Qiskit
PyQuil
Application of gates (using bloqs)
from qiskit.circuit.library.standard_gates import *
qc.append(ZGate(), qargs=[qr[2]], cargs=[])
qc.append(CHGate(), qargs=[qr[2], qr[0]], cargs=[])
qc.append(RYYGate(5.398622178940033), qargs=[qr[0], qr[2]], cargs=[])import cirq
from bloqs.ext.cirq import Gates
qc.append(cirq.Z( qr[2] ))
qc.append(cirq.H.controlled()( qr[2], qr[0] ))
qc.append(Gates.RYYGate(5.398622178940033)( qr[0], qr[2] ))from pyquil.gates import *
from bloqs.ext.PyQuil import Gates
qc.inst(Z(2))
# control qubit 2 and target qubit 0
qc.inst(H(0).controlled(2))
qc.inst(Gates.RYYGate(5.398622178940033)( 0, 2 ))Cirq
Qiskit
PyQuil
Application of gates (using bloqs)
from qiskit.circuit.library.standard_gates import *
qc.append(ZGate(), qargs=[qr[2]], cargs=[])
qc.append(CHGate(), qargs=[qr[2], qr[0]], cargs=[])
qc.append(RYYGate(5.398622178940033), qargs=[qr[0], qr[2]], cargs=[])import cirq
from bloqs.ext.cirq import Gates
qc.append(cirq.Z( qr[2] ))
qc.append(cirq.H.controlled()( qr[2], qr[0] ))
qc.append(Gates.RYYGate(5.398622178940033)( qr[0], qr[2] ))from pyquil.gates import *
from bloqs.ext.PyQuil import Gates
qc.inst(Z(2))
# control qubit 2 and target qubit 0
qc.inst(H(0).controlled(2))
qc.inst(Gates.RYYGate(5.398622178940033)( 0, 2 ))Cirq
Qiskit
PyQuil
Application of gates (using bloqs)
from qiskit.circuit.library.standard_gates import *
qc.append(ZGate(), qargs=[qr[2]], cargs=[])
qc.append(CHGate(), qargs=[qr[2], qr[0]], cargs=[])
qc.append(RYYGate(5.398622178940033), qargs=[qr[0], qr[2]], cargs=[])import cirq
from bloqs.ext.cirq import Gates
qc.append(cirq.Z( qr[2] ))
qc.append(cirq.H.controlled()( qr[2], qr[0] ))
qc.append(Gates.RYYGate(5.398622178940033)( qr[0], qr[2] ))from pyquil.gates import *
from bloqs.ext.PyQuil import Gates, get_custom_get_definitions
qc = Program()
ryy_defn = get_custom_get_definitions("RYYGate")
qc += ryy_defn
qc.inst(Z(2))
qc.inst(H(0).controlled(2))
qc.inst(Gates.RYYGate(5.398622178940033)( 0, 2 ))Cirq
Qiskit
PyQuil
Application of gates (measurement gates)
qc.append(ZGate(), qargs=[qr[2]], cargs=[])
qc.append(CHGate(), qargs=[qr[2], qr[0]], cargs=[])
qc.append(RYYGate(5.398622178940033), qargs=[qr[0], qr[2]], cargs=[])
qc.measure(qr, cr)qc.append(cirq.Z( qr[2] ))
qc.append(cirq.H.controlled()( qr[2], qr[0] ))
qc.append(Gates.RYYGate(5.398622178940033)( qr[0], qr[2] ))
qc.append(cirq.measure(qr[0], key='q0'))
qc.append(cirq.measure(qr[1], key='q1'))qc.inst(Z(2))
qc.inst(H(0).controlled(2))
qc.inst(Gates.RYYGate(5.398622178940033)( 0, 2 ))
qc += MEASURE(0, qr[0])
qc += MEASURE(1, qr[1])Cirq
Qiskit
PyQuil
Preparation of the circuit
from qiskit import transpile
qc = transpile(qc, optimization_level=2)
# other options are coupling_map, basis_gates etc.import cirq
qc = cirq.drop_empty_moments(qc)
qc = cirq.merge_k_qubit_unitaries(qc)
qc = cirq.eject_z(qc)
qc = cirq.drop_negligible_operations(qc)
executable = qvm.compile(qc, protoquil=True, optimize=True)
# some optimization available via quilc and qvm programsCirq
Qiskit
PyQuil
Execution of the circuit
from qiskit import Aer, execute
qasm_sim_backend = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=qasm_sim_backend, shots=2048)import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)from pyquil import get_qc
qc.wrap_in_numshots_loop(2048)
qc = get_qc("11q-qvm")
result = qc.run(executable)Cirq
Qiskit
PyQuil
Execution of the circuit
from qiskit import Aer, execute
qasm_sim_backend = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=qasm_sim_backend, shots=2048)import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)from pyquil import get_qc
qc.wrap_in_numshots_loop(2048)
qc = get_qc("11q-qvm")
result = qc.run(executable)Cirq
Qiskit
PyQuil
[
AerSimulator("aer_simulator"),
AerSimulator("aer_simulator_statevector"),
AerSimulator("aer_simulator_density_matrix"),
AerSimulator("aer_simulator_stabilizer"),
AerSimulator("aer_simulator_matrix_product_state"),
AerSimulator("aer_simulator_extended_stabilizer"),
AerSimulator("aer_simulator_unitary"),
AerSimulator("aer_simulator_superop"),
QasmSimulator("qasm_simulator"),
StatevectorSimulator("statevector_simulator"),
UnitarySimulator("unitary_simulator"),
PulseSimulator("pulse_simulator"),
]
Execution of the circuit
from qiskit import Aer, execute
qasm_sim_backend = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=qasm_sim_backend, shots=2048)import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)from pyquil import get_qc
qc.wrap_in_numshots_loop(2048)
qc = get_qc("11q-qvm")
result = qc.run(executable)Cirq
Qiskit
PyQuil
import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)Execution of the circuit
from qiskit import Aer, execute
qasm_sim_backend = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=qasm_sim_backend, shots=2048)import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)from pyquil import get_qc
qc.wrap_in_numshots_loop(2048)
qc = get_qc("11q-qvm")
result = qc.run(executable)Cirq
Qiskit
PyQuil
import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)Execution of the circuit
from qiskit import Aer
qasm_sim_backend = Aer.get_backend('qasm_simulator')
result = execute(qc, backend=qasm_sim_backend, shots=2048)import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)from pyquil import get_qc
qc.wrap_in_numshots_loop(2048)
qc = get_qc("11q-qvm")
result = qc.run(executable)Cirq
Qiskit
PyQuil
import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)Collection of results
result = execute(qc, backend=qasm_sim_backend, shots=2048)
counts = result.get_counts(qc)
# {'010': 66, # '000': 198, # '110': 63 ... }import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)result = qc.run(executable)
counts = result.readout_data.get('ro')
# [ [0, 1, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], ... ]Cirq
Qiskit
PyQuil
result = simulator.run(circuit, repetitions=2048)
print(result)
# q0=11011110100010101111
# q1=01100101011001110001Collection of results
result = execute(qc, backend=qasm_sim_backend, shots=2048)
counts = result.get_counts(qc)
# {'010': 66, # '000': 198, # '110': 63 ... }import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)result = qc.run(executable)
counts = result.readout_data.get('ro')
# [ [0, 1, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], ... ]Cirq
Qiskit
PyQuil
result = simulator.run(circuit, repetitions=2048)
print(result)
# q0=11011110100010101111
# q1=01100101011001110001Little- and Big-endian
qr = QuantumRegister(3, name='qr')
cr = ClassicalRegister(3, name='cr')
qc = QuantumCircuit(qr, cr, name='qc')
qc.append(HGate(), qargs=[qr[2]], cargs=[])
qc.measure(qr, cr)
# ... backend selection ...
counts = execute(qc, backend=b, shots=1024)
.result()
.get_counts(qc)
# {'100': 505, '000': 519}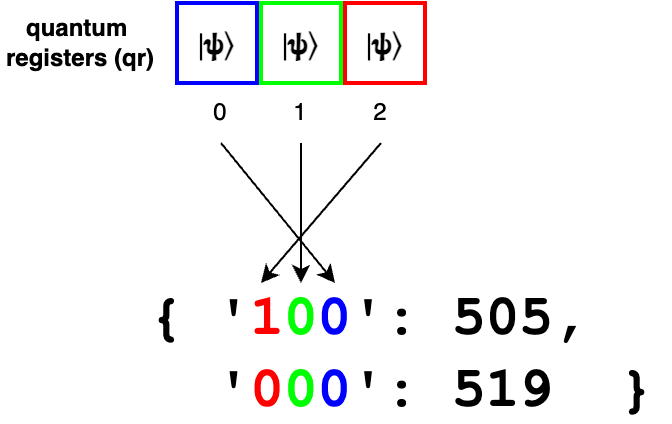
Collection of results (using bloqs)
result = execute(qc, backend=qasm_sim_backend, shots=2048)
counts = result.get_counts(qc)
# {'010': 66, # '000': 198, # '110': 63 ... }import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)from bloqs.ext.PyQuil.utils import get_qiskit_like_output
result = qc.run(executable)
counts = result.readout_data.get('ro')
output = get_qiskit_like_output(data)
# { ... }Cirq
Qiskit
PyQuil
from bloqs.ext.cirq.utils import get_qiskit_like_output
result = simulator.run(circuit, repetitions=2048)
counts = get_qiskit_like_output(result, keys=['cr0', 'cr1', 'cr2'])
# {'010': 65, # '000': 199, # '110': 66 ... }Collection of results
result = execute(qc, backend=qasm_sim_backend, shots=2048)
counts = result.get_counts(qc)
# {'010': 66, # '000': 198, # '110': 63 ... }import cirq
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=2048)from bloqs.ext.PyQuil.utils import get_qiskit_like_output
result = qc.run(executable)
counts = result.readout_data.get('ro')
output = get_qiskit_like_output(data)
# { ... }Cirq
Qiskit
PyQuil
from bloqs.ext.cirq.utils import get_qiskit_like_output
result = simulator.run(circuit, repetitions=2048)
counts = get_qiskit_like_output(result, keys=['cr0', 'cr1', 'cr2'])
# {'010': 65, # '000': 199, # '110': 66 ... }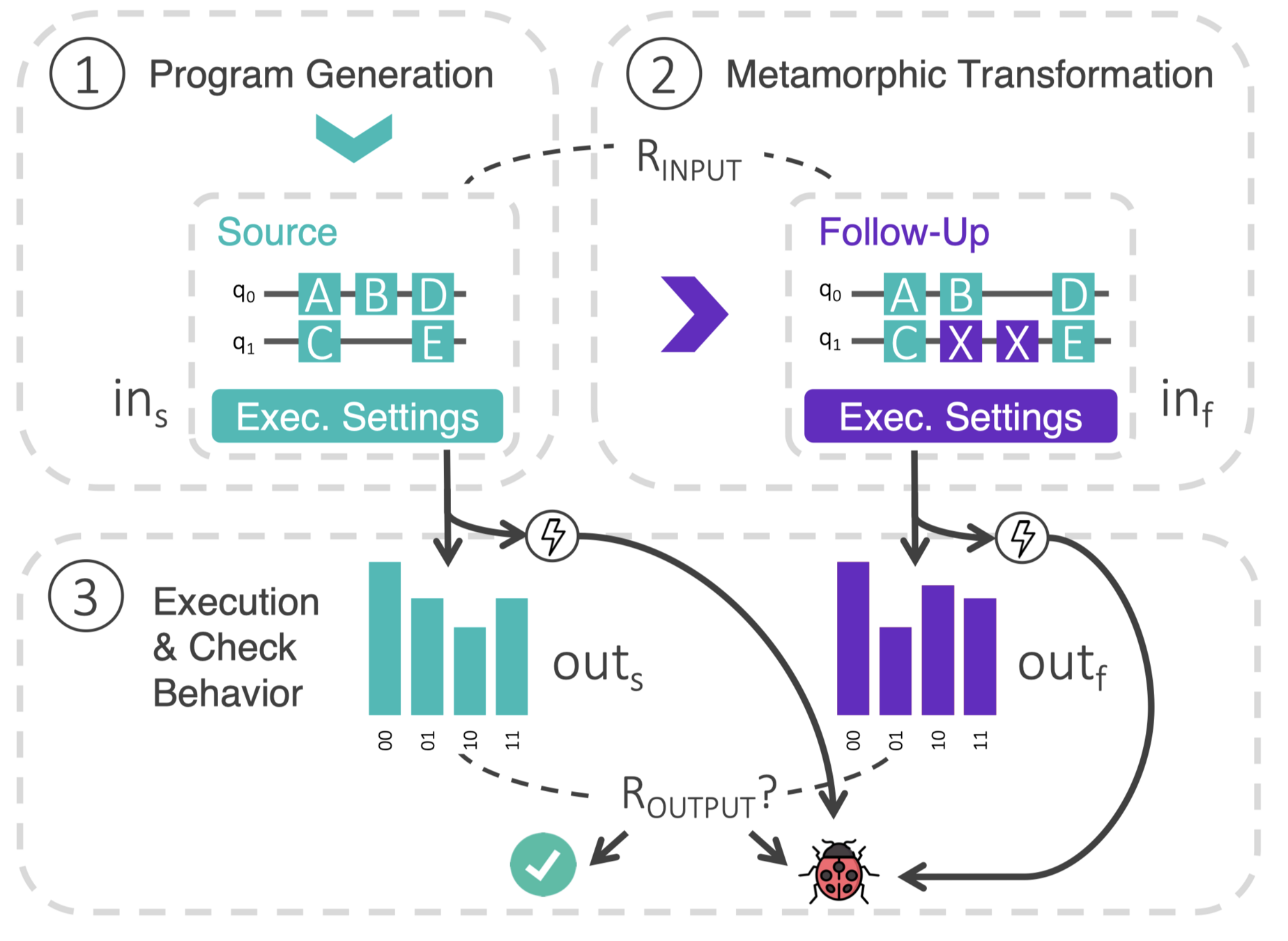
MorphQ Paper
Source Program
as passing test case
Metamorphic Testing

MorphQ Paper
Source Program
as passing test case
based on the previous MRs
Metamorphic Testing
Follow-up Porgram

MorphQ Paper
Source Program
as passing test case
Follow-up Porgram
based on the previous MRs
Execute
both and
compare
Metamorphic Testing
Metamorphic Relations (MR)
| MR | Qiskit | Cirq | PyQuil |
|---|---|---|---|
| Change Qubit Order | Y | Y | Y |
| Inject null-effect operation | Y | Y | Y |
| Add quantum register | Y | N | - |
| Inject parameters | Y | N | Y |
| Partitioned execution | Y | Y | Y |
| Intermediary language roundtrip | Y | Y | Y |
| Roundtrip conversion via QASM3 | Y | - | - |
| Serialization roundtrip | Y | Y | - |
| Change of coupling map | Y | Y | N |
| Change of gate set | Y | N | N |
| Change of optimization level | Y | Y | Y |
| Change of backend | Y | Y | Y |
Y = QSP supports given MR
N = No valid API
- = Not a valid MR in the given platform
Change Qubit Order
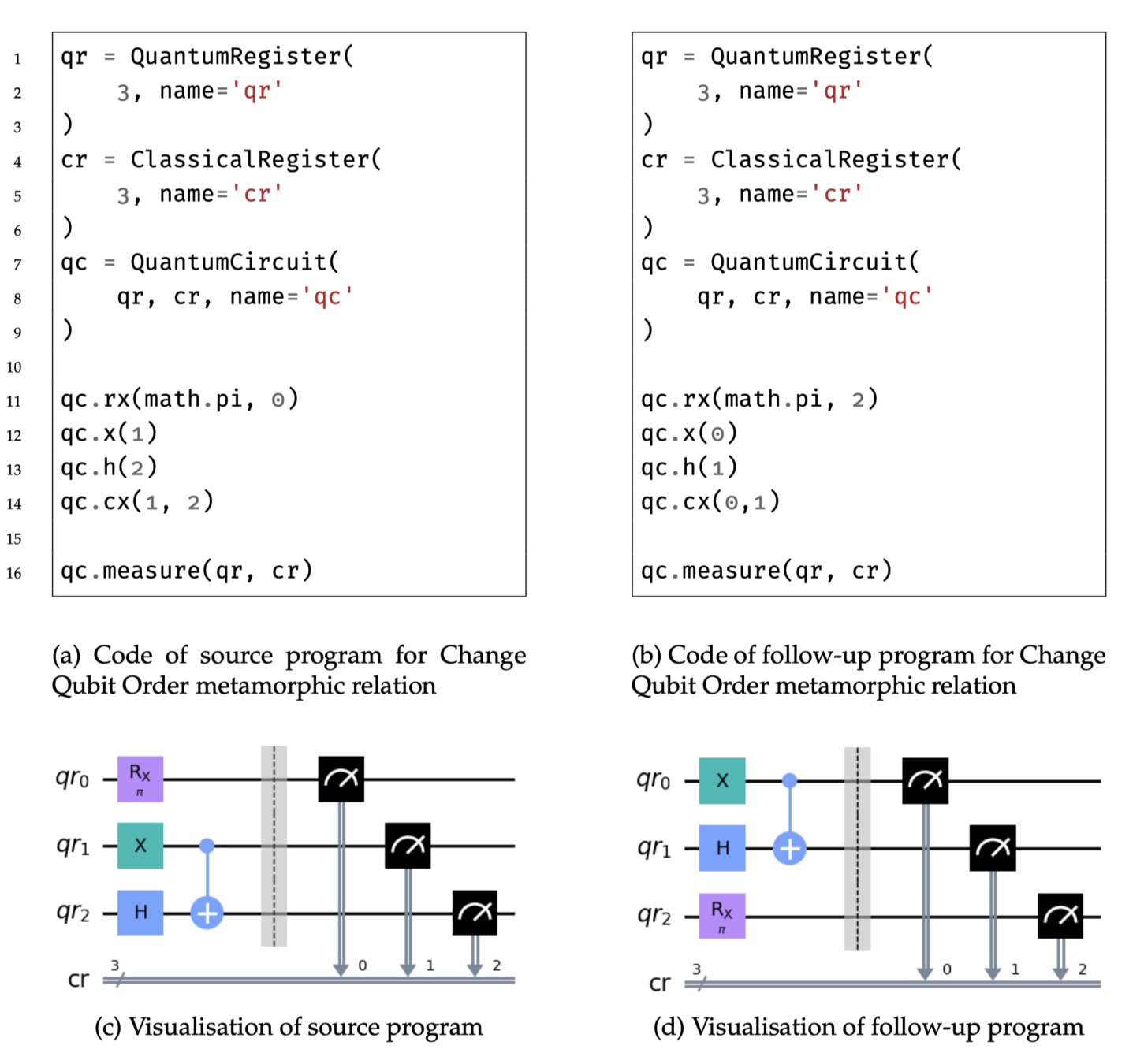
requires post-processing of the result
maps the qubit indices of source program to new positions and then creates a follow up program by adapting the sequence of gates to the newly mapped qubit indices.
Change Qubit Order

requires post-processing of the result
Change Qubit Order

requires post-processing of the result
Change Qubit Order

requires post-processing of the result
Change Qubit Order

requires post-processing of the result
Change Qubit Order

requires post-processing of the result
Change Qubit Order

requires post-processing of the result
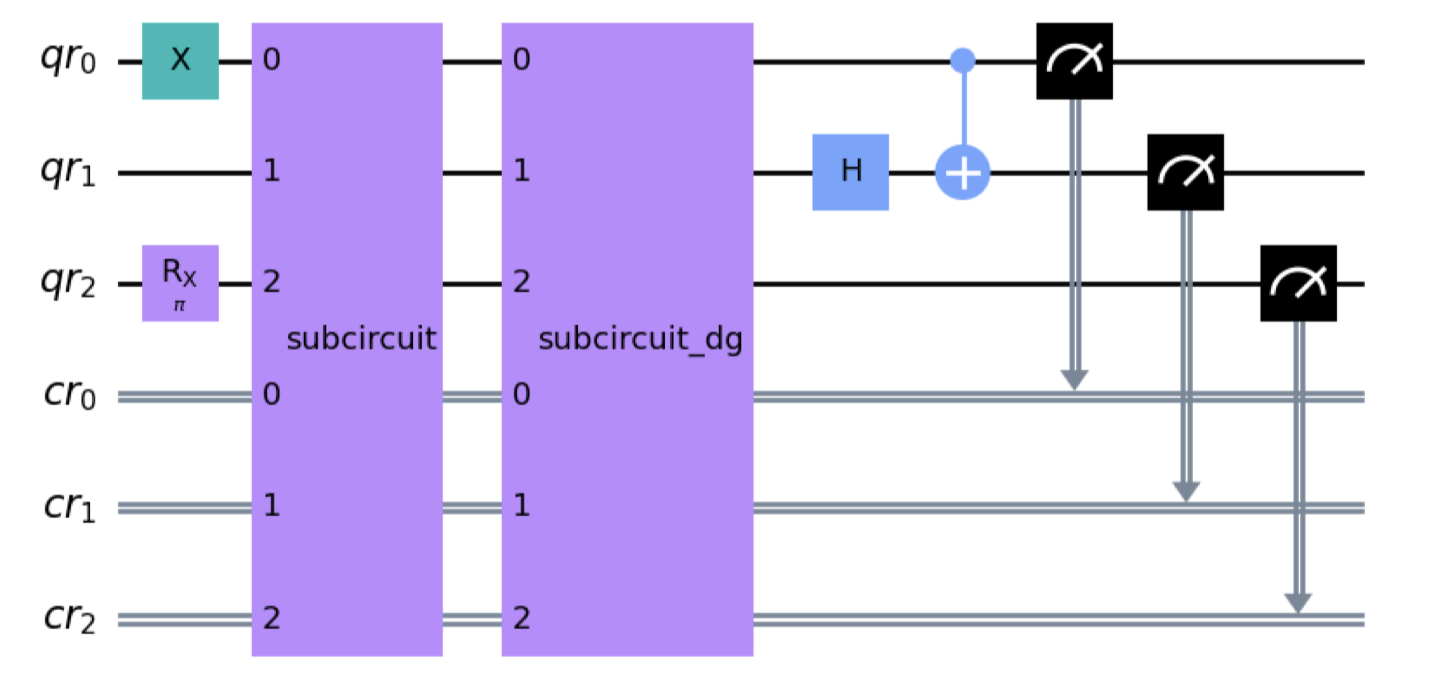
Inject null-effect operation

Inserting into the main circuit a sub-circuit that performs a sequence of gate operations followed by its inverse

Inject null-effect operation


Inserting into the main circuit a sub-circuit that performs a sequence of gate operations followed by its inverse

Inject null-effect operation


qc.rx(math.pi, 2)
qc.x(0)
subcircuit = QuantumCircuit(qr, cr, name='subcircuit')
subcircuit.append(HGate(), qargs=[qr[0]], cargs=[])
qc.append(subcircuit, qargs=qr, cargs=cr)
qc.append(subcircuit.inverse(), qargs=qr, cargs=cr)
qc.h(1) qc.cx(0,1)Inserting into the main circuit a sub-circuit that performs a sequence of gate operations followed by its inverse
Cirq
Qiskit
PyQuil
qc.append(subcircuit, qargs=qr, cargs=cr)
qc.append(subcircuit.inverse(), qargs=qr, cargs=cr)subcircuit = Program()
# add gates to sub-circuit
qc.inst(subcircuit)
qc.inst(subcircuit.dagger())qc = cirq.Circuit() # add gates to qc
subcircuit = cirq.Circuit() # add gates to sub-circuit
qc.append(subcircuit)
qc.append(cirq.inverse(subcircuit))Inject null-effect operation
Add quantum register
Enlarging the set of available qubits by adding a new and unused quantum register should not affect the computation on the existing qubits.
# Qiskit
unused_register = QuantumRegister(5, name='extra_registers')
qc.add_register(unused_register)A comparable API does not exist in Cirq and PyQuil.
Inject parameters
Parameterized quantum circuits are quantum circuits that contain one or more parameters (for example, the angle provided to RXGate) that can be adjusted without changing the overall structure of the circuit.
There are some advantages to using parameters:
- Efficiency: When using parameters, the circuit structure remains fixed, and only the parameter values change.
- Circuit Compilation: Parametrized circuits can be transpiled and optimized before the parameters are bound to specific values.
Qiskit
from qiskit.circuit import Parameter
theta = Parameter('theta')
gamma = Parameter('gamma')
qc.append(RZGate(theta), qargs=[qr[0]], cargs=[])
qc.append(U2Gate(theta, 2.12), qargs=[qr[2]], cargs=[])
qc.append(CRZGate(gamma), qargs=[qr[1], qr[0]], cargs=[])
qc.measure(qr, cr)
# before execution
qc = qc.bind_parameters({
theta: 4.2641612072511235,
gamma: 2.5163050709890156,
})Inject parameters
Qiskit
from qiskit.circuit import Parameter
theta = Parameter('theta')
gamma = Parameter('gamma')
qc.append(RZGate(theta), qargs=[qr[0]], cargs=[])
qc.append(U2Gate(theta, 2.12), qargs=[qr[2]], cargs=[])
qc.append(CRZGate(gamma), qargs=[qr[1], qr[0]], cargs=[])
qc.measure(qr, cr)
# before execution
qc = qc.bind_parameters({
theta: 4.2641612072511235,
gamma: 2.5163050709890156,
})Inject parameters
Qiskit
from qiskit.circuit import Parameter
theta = Parameter('theta')
gamma = Parameter('gamma')
qc.append(RZGate(theta), qargs=[qr[0]], cargs=[])
qc.append(U2Gate(theta, 2.12), qargs=[qr[2]], cargs=[])
qc.append(CRZGate(gamma), qargs=[qr[1], qr[0]], cargs=[])
qc.measure(qr, cr)
# before execution
qc = qc.bind_parameters({
theta: 4.2641612072511235,
gamma: 2.5163050709890156,
})Inject parameters
Qiskit
from qiskit.circuit import Parameter
theta = Parameter('theta')
gamma = Parameter('gamma')
qc.append(RZGate(theta), qargs=[qr[0]], cargs=[])
qc.append(U2Gate(theta, 2.12), qargs=[qr[2]], cargs=[])
qc.append(CRZGate(gamma), qargs=[qr[1], qr[0]], cargs=[])
qc.measure(qr, cr)
# before execution
qc = qc.bind_parameters({
theta: 4.2641612072511235,
gamma: 2.5163050709890156,
})Inject parameters
Cirq
Qiskit
from qiskit.circuit import Parameter
theta = Parameter('theta')
gamma = Parameter('gamma')
qc.append(RZGate(theta), qargs=[qr[0]], cargs=[])
qc.append(U2Gate(theta, 2.12), qargs=[qr[2]], cargs=[])
qc.append(CRZGate(gamma), qargs=[qr[1], qr[0]], cargs=[])
qc.measure(qr, cr)
# before execution
qc = qc.bind_parameters({
theta: 4.2641612072511235,
gamma: 2.5163050709890156,
})import cirq from sympy import Symbol
theta = Symbol('theta')
gamma = Symbol('gamma')
qc.append(cirq.rz(theta)(qr[0]))
qc.append(Gates.CRZGate(gamma)( qr[1], qr[2] ))
qc = cirq.resolve_parameters(qc, {
"theta": 4.2641612072511235,
"gamma": 2.5163050709890156,
"_lambda": 2.586208953975239,
})Inject parameters
Cirq
Qiskit
PyQuil
from qiskit.circuit import Parameter
theta = Parameter('theta')
gamma = Parameter('gamma')
qc.append(RZGate(theta), qargs=[qr[0]], cargs=[])
qc.append(U2Gate(theta, 2.12), qargs=[qr[2]], cargs=[])
qc.append(CRZGate(gamma), qargs=[qr[1], qr[0]], cargs=[])
qc.measure(qr, cr)
# before execution
qc = qc.bind_parameters({
theta: 4.2641612072511235,
gamma: 2.5163050709890156,
})theta = qc.declare('theta', 'REAL')
gamma = qc.declare('gamma', 'REAL')
qc.inst(RZ(theta, 0))
qc.inst(Gates.CRZGate(gamma, 1, 2 ))
params = {
"theta": 4.2641612072511235,
"gamma": 2.5163050709890156,
}
for param, value in params.items():
qc.write_memory(region_name=param, value=value)import cirq from sympy import Symbol
theta = Symbol('theta')
gamma = Symbol('gamma')
qc.append(cirq.rz(theta)(qr[0]))
qc.append(Gates.CRZGate(gamma)( qr[1], qr[2] ))
qc = cirq.resolve_parameters(qc, {
"theta": 4.2641612072511235,
"gamma": 2.5163050709890156,
"_lambda": 2.586208953975239,
})Inject parameters
Partitioned execution
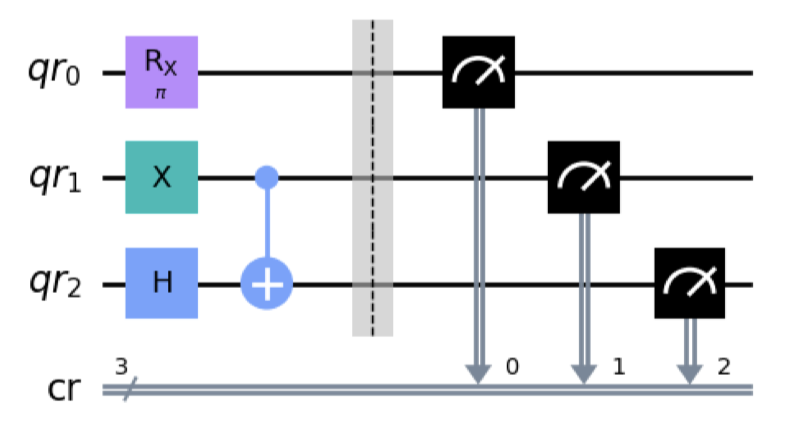
Source programs might have two subsets of qubits that never interact with each other.
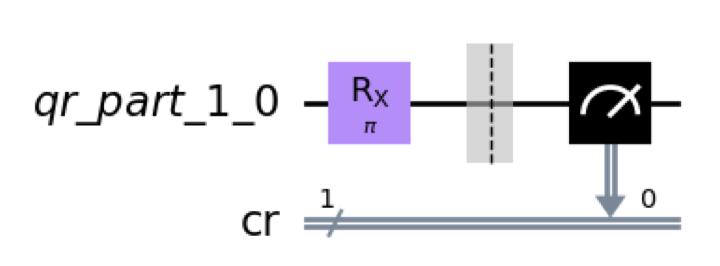
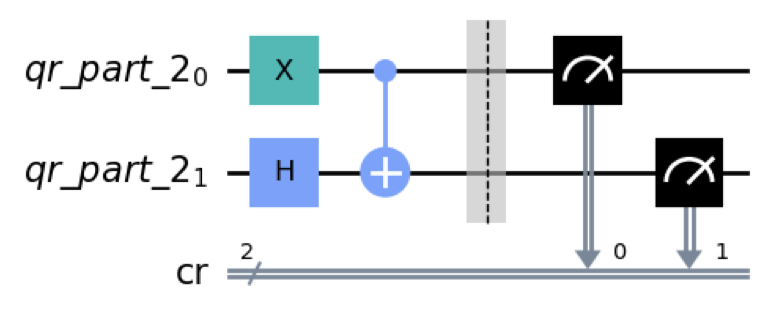
Partitioned execution

Source programs might have two subsets of qubits that never interact with each other.


- Post-Processing of results required
- No extra API required as QCross calls the circuit generation function twice.
Intermediary language roundtrip
-
Qiskit has OpenQASM2.
-
Cirq has parital support for OpenQASM2
-
PyQuil has QUIL
Cirq
Qiskit
PyQuil
qc = qc.from_qasm_str(
qc.qasm()
)from PyQuil.parser import parse
quil_str = qc.out()
qc = parse(quil_str)import cirq
from cirq.contrib.qasm_import import circuit_from_qasm
qasm_out = cirq.qasm(qc)
qc = circuit_from_qasm(qasm_out)
Round-trip conversion via QASM3
QASM 3 format is anticipated to supersede QASM 2 in the near future
Qiskit
from qiskit.qasm3 import loads, dumps
qasm3_out = dumps(qc)
qc = loads(qasm3_out)Serialization roundtrip
Serialization is defined as the process of converting the state of an object into a form that can be persisted or transported.
Cirq
Qiskit
from qiskit.circuit import QuantumCircuit from qiskit import qpy
qc = QuantumCircuit(2, name='Bell')
qc.h(0)
qc.cx(0, 1)
qc.measure_all()
with open('bell.qpy', 'wb') as fd:
qpy.dump(qc, fd)
with open('bell.qpy', 'rb') as fd:
new_qc = qpy.load(fd)[0]qc = cirq.read_json(
cirq.to_json(qc)
)Change of coupling map
- A coupling map is defined as a representation of the connectivity between the qubits in a quantum computing device.
- It describes which qubits are physically connected and can directly interact with each other through two-qubit gates, such as the controlled NOT (CNOT) gate.
q0
q1
q2
Change of coupling map
- A coupling map is defined as a representation of the connectivity between the qubits in a quantum computing device.
- It describes which qubits are physically connected and can directly interact with each other through two-qubit gates, such as the controlled NOT (CNOT) gate.
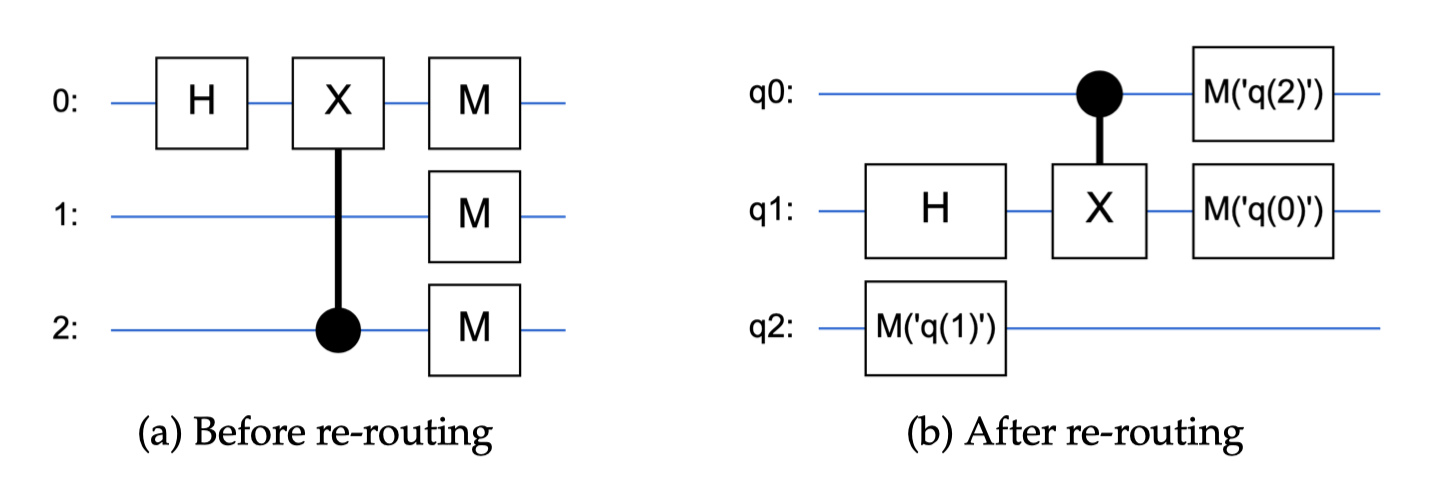
q0
q1
q2
Change of coupling map
- A coupling map is defined as a representation of the connectivity between the qubits in a quantum computing device.
- It describes which qubits are physically connected and can directly interact with each other through two-qubit gates, such as the controlled NOT (CNOT) gate.

q0
q1
q2
Change of coupling map
Cirq
Qiskit
# Define a custom coupling map
custom_coupling_map = [[0, 1], [1, 2], [2, 3]]
# Transpile the circuit using the custom coupling map
transpiled_qc = transpile(qc, coupling_map=custom_coupling_map)import networkx as nx
def edge_list_to_cirq_graph(edge_list, nodes=None):
if nodes is None:
num_qubits = len(
set(item for sublist in edge_list for item in sublist)
)
nodes = [
cirq.NamedQubit("q" + str(i)) for i in range(num_qubits)
]
graph = nx.Graph()
for n in nodes:
graph.add_node(n)
for e in edge_list:
graph.add_edge(nodes[e[0]], nodes[e[1]])
return graph
graph = edge_list_to_cirq_graph(qc)
router = cirq.RouteCQC(graph)
routed_qc = router(qc)Change of gate set
This transformation exercise this translation step by replacing the circuit gates in the program with a universal gate set, such as ["rx", "ry", "rz", "p", "cx"]
Qiskit
from qiskit import QuantumCircuit, transpile
qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)
custom_basis_gates = ['rx', 'ry', 'rz', 'p', 'cx']
transpiled_qc = transpile(qc, basis_gates=custom_basis_gates)Change of optimization level
Similar to modifying the optimization level of a traditional compiler, we can change the optimization level of the quantum transpilation process.
Qiskit
from qiskit import QuantumCircuit, transpile
qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)
transpiled_qc = transpile(qc, optimization_level=1)Cirq
qc = cirq.eject_phased_paulis(qc)- cirq.align_left / cirq.align_right
- cirq.drop_empty_moments / cirq.drop_negligible_operations
- cirq.eject_phased_paulis
- cirq.eject_z
- cirq.expand_composite
- cirq.merge_k_qubit_unitaries
- cirq.stratified_circuit
Change of backend
Different simulators typically have completely different implementations, such as one based on state vectors or density matrices.
- Qiskit
- many
- Cirq
- Simulator
- DensityMatrixSimulator
- PyQuil
- 9q-square-qvm
- Xq-qvm
Differential Testing
- Unitary Matrix Comparison
- Cirq Qiskit Rountrip
- Output comparison
- All Source Output
- All Follow-up Outputs
Unitary Matrix Comparison
- A quantum gate can be represented by a unitary matrix.
- The application of multiple quantum gates preserves unitarity.
- When two quantum circuits possess the same gates and an equal number of qubits, their respective unitary matrices will be equivalent, modulo a global phase and a same starting qubit states.
Qiskit
Cirq
UNITARY = cirq.unitary(qc)backend = Aer.get_backend('unitary_simulator')
result = execute(qc.reverse_bits(), backend=backend).result()
UNITARY = result.get_unitary(qc).datafrom pyquil.simulation.tools import program_unitary
# 6 is the number of qubits
UNITARY = program_unitary(circuit, 6)PyQuil
numpy.allcose or cirq.equal_up_to_global_phase
Cirq Qiskit Rountrip
- Cirq’s follow-up program is converted to QASM using the cirq.qasm function.
- It is ingested by QuantumCircuit.from_qasm_str to create a Qiskit circuit.
- The Qiskit circuit is then exported to QASM using the qasm method.
- Finally, Qiskit’s QASM is fed into Cirq to generate a Cirq circuit using the circuit_from_qasm.
Cirq has limited but growing support for QASM 2 interoperability. Therefore, this rountrip tests Cirq QASM’s generation capabilities, and Qiksit’s foreign QASM ingestion capabilities.
import cirq
from cirq.testing import *
expanded_circuit = cirq.expand_composite(circuit)
qasm_from_qiskit = qiskit.QuantumCircuit.from_qasm_str(
cirq.qasm(expanded_circuit)
).qasm()
cirq_circuit_from_qiskit_qasm = circuit_from_qasm(
qasm_from_qiskit
)
# since, importing in cirq uses different qubit names,
# we need to change the qubit names
circuit_transformed = cirq_circuit_from_qiskit_qasm.transform_qubits(
lambda q: cirq.NamedQubit(q.name.replace("q_", "q"))
)
assert_circuits_with_terminal_measurements_are_equivalent(
circuit_transformed,
circuit
)Outputs Equivalence Check
Given that each set contains three programs (3 sources and 3 followfups), we carry out pairwise assessments per set, resulting in a total of six comparisons.
Comparing Execution Behavior
- We use the Kolmogorov-Smirnov test to assess the statistical significance of the difference between the two distributions, as done in previous work, using a significance level of α = 5%. We call any pair of programs with a p-value below α a statistically significant distribution difference.
- Source or follow-up crash is termed as crash difference.
Arrange
Assert
Act


We expanded MorphQ’s Qiskit gate-set by incorporating following new available gates: CCZGate, CSGate, CSdgGate, RGate, and RVGate.























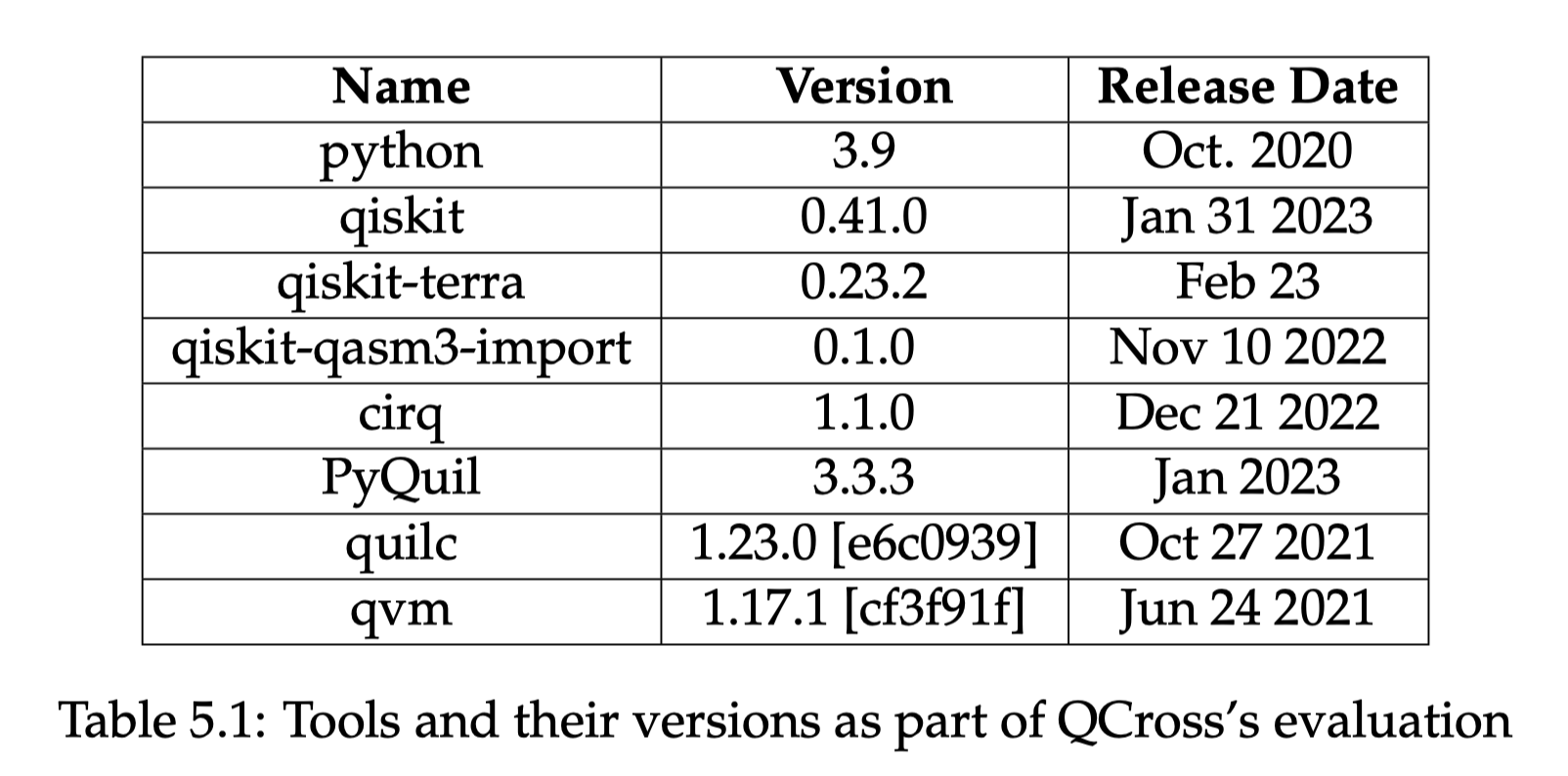
Tools and Test-bed
All experiments were run on an Apple M1 Pro 14-inch (2021 model) machine. It has ten cores (eight high-performance and two energy efficient), and 16 GB RAM. The OS at the time of evaluation was MacOS Ventura 13.3.1 (22E261)






Arrange
Assert
Act
Research Questions
-
RQ1: How many syntactically different but correct programs can be translated by QCross’s converter?
-
RQ2: What has QCross found via cross-platform testing of the widely-used QSSes? i.e., how many warnings and errors do QCross produce?
-
RQ3: How does QCross compare to prior work on testing quantum computing platforms?
- RQ4: How useful is Bloqs?
RQ1
We did not record any crashes during the translation process.
How many syntactically different but correct programs can be translated by QCross’s converter?
The program converter successfully translates only valid quantum programs, ensures that any possible metamorphic relation is maintained, and QCross is effective in producing numerous warnings and crashes in follow-up programs of different platforms when executed.
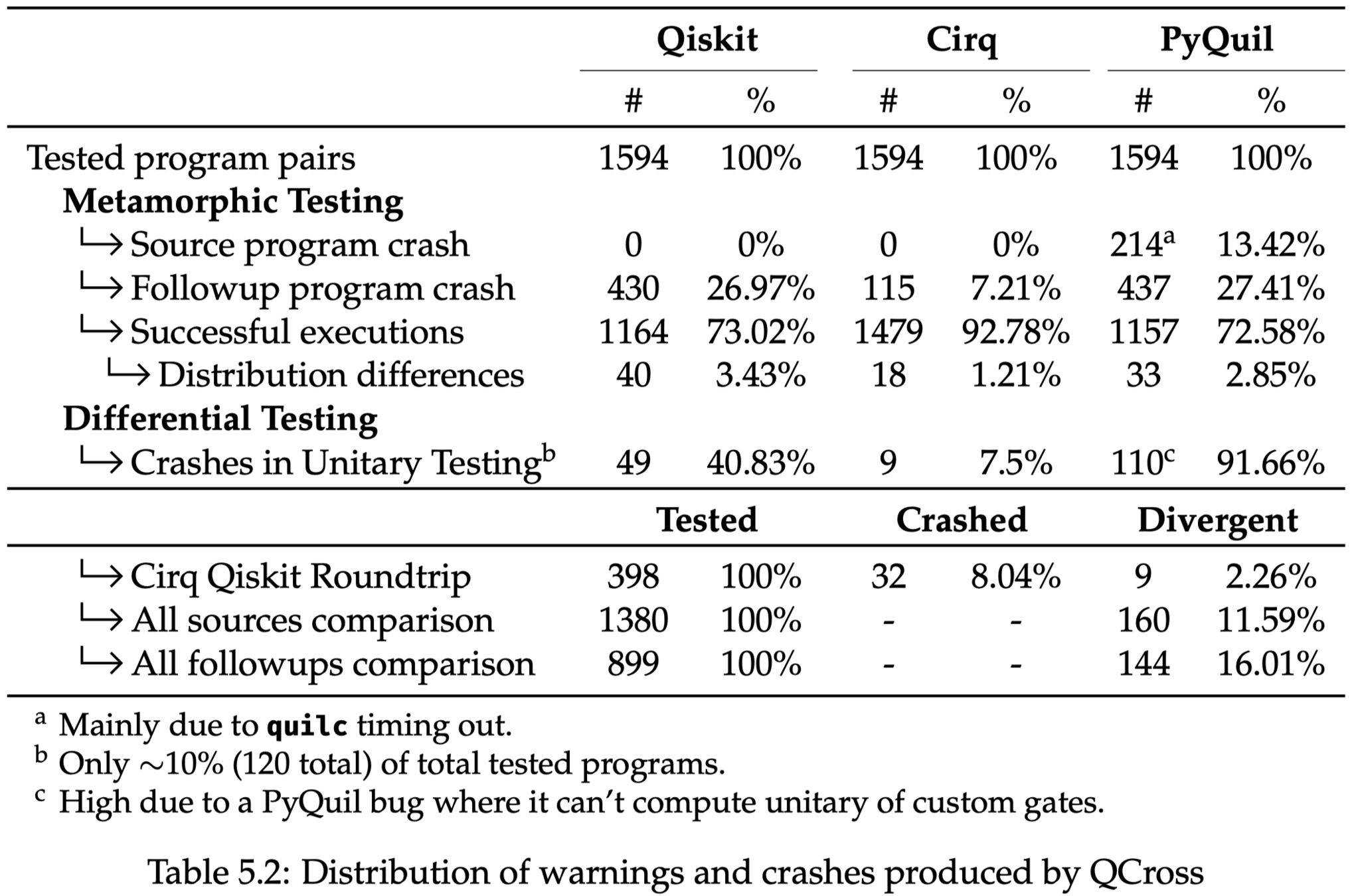
RQ2
QCross identified 14 bugs and 2 potential issues across quantum programming platforms, with Qiskit (8) having the most bugs, followed by PyQuil (4) and Cirq (2).
What has QCross found via cross-platform testing of the widely-used QSSes? i.e., how many warnings and errors do QCross produce?















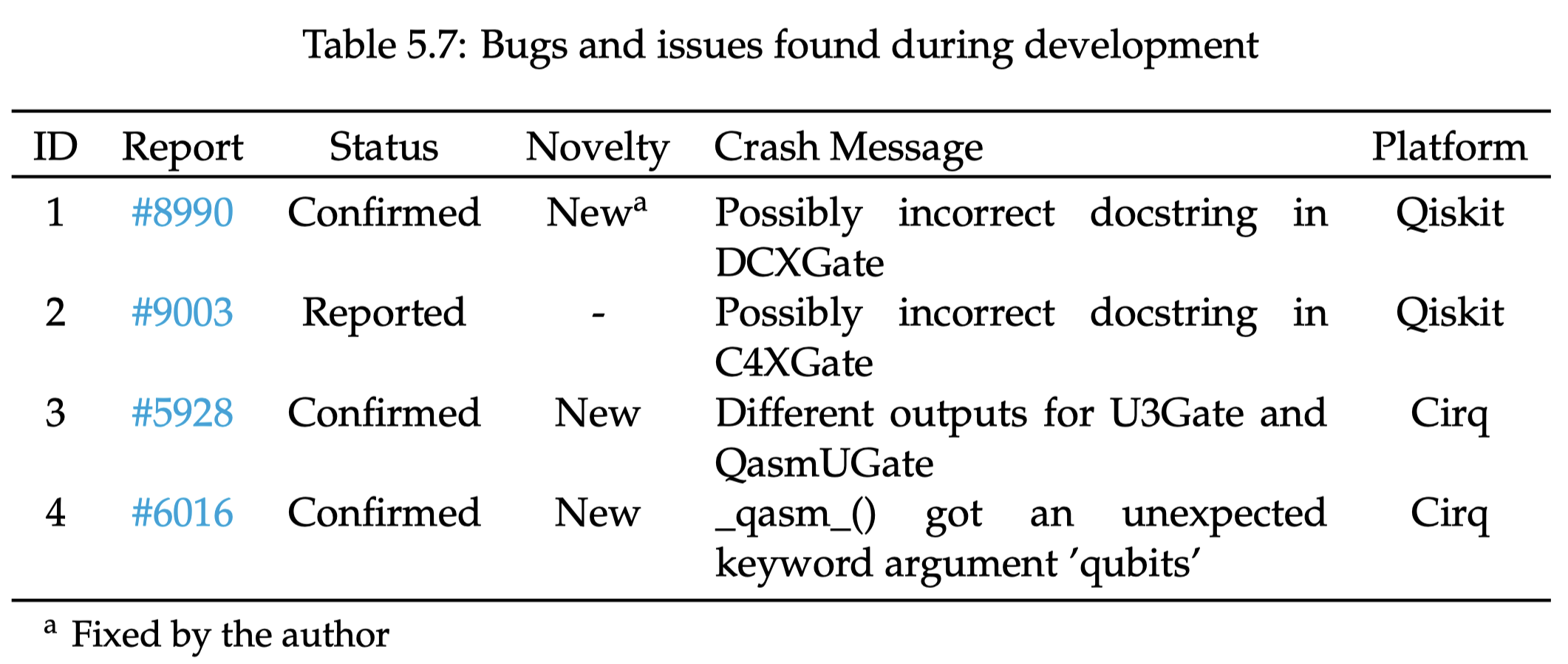
QCross identified 14 bugs and 2 potential issues across quantum programming platforms, with Qiskit (8) having the most bugs, followed by PyQuil (4) and Cirq (2).
Metamorphic testing proved more effective than differential testing, and ten of the reported bugs have been confirmed as novel by developers.
RQ3
We regard QCross as an "evolutionary successor" to MorphQ and QDiff. It has uncovered new bugs that were not detected in the previous works, demonstrating its complementary value to the existing research.
How does QCross compare to prior work on testing quantum computing platforms?
- More platforms
- New bugs
- New MRs and extra gates
- bloqs as a utility library
RQ4
The bloqs library was developed to overcome gate set limitations in Cirq and PyQuil, enabling successful translation of Qiskit programs. The library proved essential, as it was required in approximately 94% of translations.
How useful is Bloqs?
Future Works
- Ensure the generated programs are more "real-world" programs.
- Extend the number of tested platforms to include non-python platforms as well.
- Execute the programs on quantum hardware to establish a source of truth or to find bugs in the hardware.
-
Devise a method to better test the divergence of program outputs such that false positives are minimized.
-
Analyse the existing divergent programs to find out the source of divergence.
Thank you!
QCross
By Arfat Salman
QCross
This presentation introduces QCross, a quantum cross-platform testing framework. Learn why quantum computing is important, see examples of quantum algorithms, and discover the challenges of testing quantum circuits. Explore differential and metamorphic testing methods.
- 404



