Functional Programming
Armin Taheri
Contents
- Functional vs. Imperative Programming
- Hindley-Milner type system and Currying (Haskell Types)
- Type Classes (Eq, Ord, Num, Functor, Monad, Applicative)
- Useful functional programming libraries in Javascript
Imperative
Functional
double mysqrt(int n, double x) {
double x_last = 1.0;
double f = x_last * x_last - x;
double df = (2 * x_last);
for (int i = 0; i < n; i++) {
x_last = x_last - f / df ;
f = x_last * x_last - x;
df = 2 * x_last;
}
return x_last;
}
sqrt(1000, 5) // 2.236068mysqrt 0 x = 1.0
mysqrt n x = x_last - f / df
where
x_last = mysqrt (n-1) x
f = x_last * x_last - x
df = 2 * x_last
mysqrt 1000 5 -- 2.23606797749979Imperative
double mysqrt(int n, double x) {
First assign 1.0 to x_last
Then compute x_last*x_last - x and store it into f
Then compute 2 * x_last and store it into df
then for n iterations do:
compute x_last - f / df and store it into x_last
return x_last
}
Functional
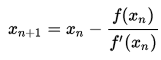
You declare what your function maps its arguments to and nothing more.
Imperative
Pros:
- Full control over execution of code.
- A perfect programmer can yield the highest performance code with optimal memory requirements.
- Simpler to compile into a sequence of machine code steps.
Functional
Pros:
- Code is declarative so execution strategy is not meant to be a concern.
- Pure functions (side effect free) always map arguments to the same thing so functions can be cached.
- The function's dependencies are made explicit in the arguments. There is no global state or references to an object's state.
- Pure functions can run in parallel since they only operate within their stack frame and have read only access to inputs.
Imperative
Cons:
- You can mutate memory anytime anywhere
- You have to explicitly state what steps yield the correct execution of your program.
- You cannot assume functions will map the same input to the same output after several calls
- Inlining a function is a complex static analysis problem.
Functional
Cons:
- Not always clear how much memory an expression requires.
- Very steep learning curve especially with complicated type systems.
- Very different from what most current developers do in practice. (for now)
- Very difficult without a good type system and good language support.
Functional Programming in Object Oriented Languages
- We want reusable, composable, and low coupled codebases.
- We want cohesion in our codebase.
- We want abstractions to deal with at most one concern.
- We want explicit dependency passing.
- We don't want singletons and global variables.
- We want to effectively unit test our abstractions.
class Stack {
constructor() {
this.stack = []
}
push(a) {
this.stack[this.stack.length] = a;
}
pop() {
var out = this.stack[this.stack.length-1];
delete this.stack[this.stack.length-1];
this.stack.length -= 1;
return out;
}
}
// We now have to test
// many possible execution paths
var s = new Stack();
s.push(3)
s.pop() // 3
s.pop() // Error!// General
var copyArray = function (array) {
return array.slice(0, array.length);
}
var append = function (value, array) {
var newArr = copyArray(array);
newArr[newArr.length] = value;
return newArr
}
var removeAt = function (n, array) {
var newArr = copyArray(array);
newArr.splice(n, 1);
return [array[n], newArr];
}
// Stack
var push = append;
var pop = function (array) {
return removeAt(array.length-1, array);
}
// Queue
var queue = append;
var dequeue = function (array) {
return removeAt(0, array);
}Hindley Milner Type System
- We need a way to communicate a function's type as efficiently as possible.
- We would like to immediately know if a function or value could be composed or used as a dependency of another function.
- We want to do this without reading a paragraph of documentation.
Hindley Milner Type System
4.0 * 4.0 :: Double
mysqrt :: Double -> Double
toUpper :: String -> String
strLength :: [Char] -> Int
(+) :: Number -> Number -> NumberWe either have values or functions. Value types are denoted as:
expression :: Type
Function types are denotes as
expression :: Type -> ... -> Type
Parametric Polymorphism
identity :: a -> a
identity x = xFunctions do not need to have a concrete type for its arguments. Think of the identity function:
The type 'a' could be anything as long as we are consistent whenever 'a' shows up in the type.
Function application and composition
When a function f :: a -> b is applied to an expression e :: a,
we get an expression (f e) :: b
When a function f :: a -> b
and a function g :: b -> c
are composed, we get a function
(f . g) :: a -> c
Composition is how pipelines are created in functional programs.
Function application and composition
With these laws it does not take more than knowing the type of a function to know how to apply and compose it in a larger abstraction.
Often we can debug a dynamically typed programming language just by logically applying the application and composition inference rules for function types.
Currying
add :: (Number, Number) -> Number
add (1, 1) :: Number
(addCurry) :: Number -> (Number -> Number)
(addCurry 1) :: Number -> Number
((addCurry 1) 1) :: NumberFunctions are typically seen as taking a tuple (x1, x2, ..., xn) and mapping to a result.
These functions can be "curried" so that they can be partially applied. We can see this as "configuring" a function before applying it to it's final argument.
Type Classes
Type classes allow us to add assumptions to the type of a function without restricting the actual type of the function.
It is good practice to create data structures that conform to one or more type classes so libraries can be written more generally.
Type Classes
Javascript does not have type classes but we can still keep them in mind when coding. Examples are:
Eq a
-- the type 'a' must have a way to equate two values of type 'a'.
Ord a
-- the type 'a' must have a way to order elements of 'a'.
Num a
-- the type 'a' must have arithmetic operations defined.Type Classes
We can now add assumtions about the inputs of our function:
addNums :: Num a => a -> a -> a
sort :: Ord a => [a] -> [a]Type Classes
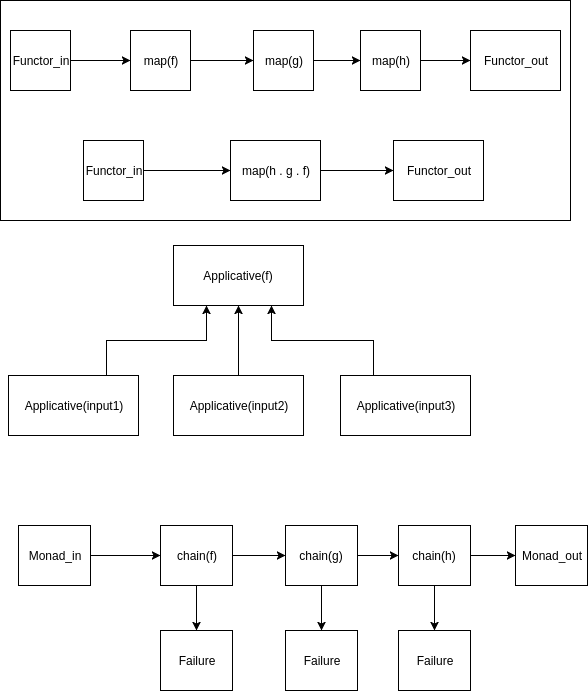
In functional programming we have more abstract type classes which allow us to write more modular functions.
One of these is the Functor typeclass. A functor instance wraps another type inside a context.
map :: Functor f => (a -> b) -> f a -> f b
map(identity, list) === list
map(f, map(g, list)) === map((f . g), list)
-- Examples:
data List a = Cons a (List a) | Nil
-- Cons 1 (Cons 2 (Cons 3 (Nil)))
instance Functor List where
map f Nil = Nil
map f Cons x xs = Cons (f x) (map f xs)
data Maybe a = Just a | Nothing
instance Functor Maybe where
map f Nothing = Nothing
map f (Just x) = Just (f x)Form Example
We will implement a form in javascript using the functional programming approach.
We start by defining the Maybe Functor
var Just = function (value) {
return {
value: value,
map: function (f) {
return Just(f(value));
}
};
};
var Nothing = {
map: function() {
return Nothing;
}
};Form Example
We then define a general map function for all functors
// map: Functor f => (a -> b) -> f a -> f b
var map = function (f){
return function (m) {
return m.map(f);
}
};Form Example
Now we define a function that checks of a string's first letter is capitalized and return Just(string) if it's valid and Nothing if it's invalid
// nameValidation: String -> Maybe String
var nameValidation = function (s) {
if (s.match('[A-Z]\w*') === null) {
return Nothing;
}
return Just(s);
};Form Example
Our Side-Effecting code are seperated into their own functions
// print: String -> Effect ()
var print = function (message) {
document.querySelector('#log').innerHTML += '<li>' + message + '</li>';
};
// clearLog: () -> Effect ()
var clearLog = function () {
document.querySelector('#log').innerHTML = '';
};Form Example
Our main form code runs in the submit function. It attemps to validate the name and map the print function on the ouput. If the output is Nothing then the mapped function is not called.
// submit: Maybe (Effect ())
function submit () {
var vname = nameValidation(document.querySelector('.name-input').value);
clearLog();
map(print)(vname);
}Form Example
We now have a validated input field.
Applicative Functors
Often we would like to validate inputs and combine them in a function that takes many arguments. Applicative functors are used to wrap these functions when we want to apply them on wrapped values.
ap :: Applicative m => m (a -> b) -> m a -> m b
of :: Applicative m => a -> m a
ap(of(identity), m) === m
ap(of(f), of(x)) = of(f(x))
-- Example:
data Maybe a = Just a | Nothing
instance Applicative Maybe where
of x = Just x
ap Nothing any = Nothing
ap any Nothing = Nothing
ap (Just f) (Just x) = Just (f x)
-- ap(of(+), (Just 1)) === (Just 3)
-- ap(of(+), Nothing) === Nothing
Form Example
Let's try to validate emails too.
We extend the definition of Just and Nothing to include the 'ap' function
var Just = function (value) {
return {
type: 'JUST',
value: value,
...
ap: function (m) {
return m.map(value);
}
};
};
var Nothing = {
type: 'NOTHING',
...
ap: function() {
return Nothing
}
};Form Example
We define a general 'ap' function for Applicative Functors.
// ap: Applicative f => f (a -> b) -> f a -> f b
var ap = function (m1) {
return function (m2) {
return m1.ap(m2);
}
};
// ES6 arrow functions:
const ap = m1 => m2 => m1.ap(m2);Form Example
We generalize validation:
// validate: Regex -> String -> Maybe String
var validate = function(r) {
return function (s) {
if (s.match(r) === null) {
return Nothing;
}
return Just(s);
}
}
// nameValidation: String -> Maybe String
var nameValidation = validate(/[A-Z]\w*/);
// emailValidation: String -> Maybe String
var emailValidation = validate(/\w+\@\w+/);
// ES6:
const validate = r => s => {
if (s.match(r) === null) {
return Nothing;
}
return Just(s);
}Form Example
And we have our input combiner:
// userToString: String -> String -> String
var userToString = function (name) {
return function (email) {
return '[Name: ' + name + ', Email: ' + email + ']';
};
};
// ES6:
const userToString = name => email =>
'[Name: ' + name + ', Email: ' + email + ']';Notice in our types: We don't expect Maybe String
Our function does not assume anything about its input except that it's a String.
Form Example
We need to upgrade our combiner to type:
Maybe String -> Maybe String -> Maybe String
// lift: Applicative f => (a -> b -> c) -> (f a -> f b -> f c)
var lift = function (op) {
return function (m1) {
return function (m2) {
return ap(map(op)(m1))(m2);
}
}
};
// ES6:
const lift = op => m1 => m2 => ap(map(op)(m1))(m2);'lift' is a general transformation from binary operators to Applicative operators
Form Example
We can then print our wrapped user and email using the map function
var userString = lift(userToString)(vname)(vemail);
map(print)(userString);Form Example
Now we can combine validated input fields!
Form Example
We can use a more descriptive Applicative called Validated:
var Success = function (value) {
return {
type: 'SUCCESS',
value: value,
map: function (f) {
return Success(f(value));
},
ap: function (m) {
return m.map(value);
}
};
};
var Failure = function (errors) {
return {
type: 'FAILURE',
value: errors,
map: function() {
return Failure(errors);
},
ap: function(m) {
switch (m.type) {
case 'SUCCESS':
return Failure(errors);
case 'FAILURE':
return Failure(errors.concat(m.value));
}
}
};
};Form Example
We can now return error values from our validation functions.
// validate: (Regex, [String]) -> String -> Validated String
var validate = function(r, errors) {
return function (s) {
if (s.match(r) === null) {
return Failure(errors);
}
return Success(s);
};
};
// nameValidation: String -> Validated String
var nameValidation = validate(/[A-Z]\w*/, ['Name must begin capitalized']);
// emailValidation: String -> Validated String
var emailValidation = validate(/\w+\@\w+/, ['Email must have form XXX@XXX']);Form Example
The Validated implementation for 'ap' handles error accumulation for us to log later:
// printValidated: Validated String -> Effect ()
var printValidated = function (validated) {
switch (validated.type) {
case 'SUCCESS':
return print(validated.value);
case 'FAILURE':
return validated.value.forEach(print);
}
};
var userString = lift(userToString)(vname)(vemail);
printValidated(userString);Form Example
And our errors will now log!
Monads
We often need to call API's from systems that may fail. The Monad typeclass can model these failures in a datatype and sequence operations that may fail.
chain :: Monad m => m a -> (a -> m b) -> m b
of :: Monad m => a -> m a
chain(of(x), f) === f(x)
chain(m, of) === m
-- join flattens nested monads
join :: Monad m => m (m a) => m a
-- Example:
data Maybe a = Just a | Nothing
instance Applicative Maybe where
of x = Just x
chain Nothing any = Nothing
chain (Just x) f = f x
join m = chain m identity
Form Example
We extend the Validated typeclass to allow chaining:
var Success = function (value) {
return {
type: 'SUCCESS',
value: value,
...
chain: function (f) {
return f(value);
}
};
};
var Failure = function (errors) {
return {
type: 'FAILURE',
value: errors,
...
chain: function () {
return Failure(errors);
}
};
};Form Example
We wrap our DBMS API with functions that handle failure using the Validated monad.
var getUsersDB = function (db) {
try {
return Success(db.getAll());
} catch (e) {
return Failure([e.message]);
}
};
// createUserDB: DB -> String -> Validated Number
var createUserDB = function (db) {
return function (name) {
try {
return Success(db.addUser(name));
} catch (e) {
return Failure([e.message])
}
};
};Form Example
We wrap our DBMS API with functions that handle failure using the Validated monad.
// setEmailDB: DB -> String -> Number -> Validated Number
var setEmailDB = function (db) {
return function (email) {
return function (id) {
try {
return Success(db.setEmail(id, email));
} catch (e) {
return Failure([e.message]);
}
};
};
};Form Example
We have our combining function that takes name and email and creates a user in the database:
// newUserDB: DB -> String -> String -> Validated Number
var newUserDB = function (db) {
return function (name) {
return function (email) {
return createUserDB(db)(name).chain(setEmailDB(db)(email));
// Or equivelently
// createUserDB(db)(name).chain(function (id) {
// return setEmailDB(db)(email)(id);
// })
//
};
};
};Notice the type: We don't assume the input is wrapped in Validated. We need to lift the newUserDB function.
Form Example
lift(newUserDB(db))(vname)(vemail) :: Validated (Validated [String])
join(lift(newUserDB(db))(vname)(vemail)) :: Validated [String]But this means if we lift newUserDB we will get a nested monad:
'join' will flatten the monad so that if input validation fails, we see those errors, otherwise we'll see errors if the DB fails. If all goes well the DB is updated.
Form Example
// userToString: User -> String
var userToString = function (user) {
return '[ Name: ' + user.name + ', Email:' + user.email + ' ]'
};
// printUsers: Validated [User] -> Effect()
var printUsers = function (users) {
switch(users.type) {
case 'SUCCESS':
var userStrings = map(userToString)(users.value)
return map(print)(userStrings);
case 'FAILURE':
return users.value.map(print);
}
};We now need a way to print the users in the database or the errors that accumulate.
Form Example
// db: DB
var db = new Database();
// submit: Validated (Effect ())
function submit() {
var vname = nameValidation(document.querySelector('.name-input').value);
var vemail = emailValidation(document.querySelector('.email-input').value);
var users =
join(lift(newUserDB(db))(vname)(vemail))
.chain(function() { return getUsersDB(db); });
clearLog();
printUsers(users);
}We can initialize our database and wait for input:
Form Example
We now have a form that saves to the database and shows errors:
Where to go from here
- Fantasy Land Specification
- Ramda
- Ramda Fantasy
- ImmutableJS
- safety-lens
- Examples:
Functional Programming
By Armin Taheri
Functional Programming
- 168


