DESI 2024: Cosmological Parameters from the Baryon Acoustic Oscillations
Arnaud de Mattia
on behalf of the DESI collaboration
Key Project led by Eva Mueller and Dragan Huterer
Moriond, April 4th
Thanks to our sponsors and
72 Participating Institutions!
- transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
BAO measures ratios of distances over the sound horizon scale at the drag epoch ["standard ruler"] \(r_\mathrm{d}\)
z
\theta_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{M}(z)
BAO measurements
- transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
- along the line-of-sight: \(D_\mathrm{H}(z) / r_\mathrm{d} = c / (H(z) r_\mathrm{d}) \)
z
\Delta z_\mathrm{BAO} = r_\mathrm{d} / D_\mathrm{H}(z)
BAO measurements
BAO measures ratios of distances over the sound horizon scale at the drag epoch ["standard ruler"] \(r_\mathrm{d}\)
- transverse to the line-of-sight: \(D_\mathrm{M}(z) / r_\mathrm{d}\)
- along the line-of-sight: \(D_\mathrm{H}(z) / r_\mathrm{d} = c / (H(z) r_\mathrm{d}) \)
- isotropic average: \( D_\mathrm{V}(z) / r_\mathrm{d} = (z D_{\mathrm{M}}^{2}(z) D_\mathrm{H}(z))^{1/3} / r_\mathrm{d}\)
BAO measurements
BAO measures ratios of distances over the sound horizon scale at the drag epoch ["standard ruler"] \(r_\mathrm{d}\)
Let's factor out the \(h\) terms:
- \(\color{blue}{[D_\mathrm{M}(z) h] (\Omega_\mathrm{m}, \Omega_\mathrm{K}, ...)} \color{black}{/} \color{orange}{[r_\mathrm{d}(\Omega_\mathrm{m} h^{2}, \Omega_\mathrm{b} h^{2}) h]} \)
- \( \color{blue}{[D_\mathrm{H}(z) h] (\Omega_\mathrm{m}, \Omega_\mathrm{K}, ...)} \color{black}{/} \color{orange}{[r_\mathrm{d}(\Omega_\mathrm{m} h^{2}, \Omega_\mathrm{b} h^{2}) h]} \)
BAO measurements at different \(z\) constrain:
- energy content \( \color{blue}{(\Omega_\mathrm{m}, \Omega_\mathrm{K}, ...)} \)
- constant-over-\(z\) product \(\color{orange}{r_\mathrm{d} h}\) i.e. \(\color{orange}{H_{0} r_\mathrm{d}}\)
These quantities directly relate to base cosmological parameters
BAO measurements
Dark energy equation of state:
\(P = w \rho\)
- \(w\) = constant
BAO measurements: dark energy
BAO measurements: dark energy
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
DESI Y1 BAO
DESI BAO measurements
Consistent with each other,
and complementary
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.295 \pm 0.015 & \mathbf{(5.1\%)} \\
H_{0} r_\mathrm{d} &= (101.8 \pm 1.3) \, [100 \, \mathrm{km} \, \mathrm{s}^{-1}] & \mathbf{(1.3\%)}
\end{align*}}_{\textstyle \text{\color{black}{DESI}}}
Consistency with other probes
DESI Y1 BAO consistent with:
Consistency with other probes
DESI Y1 BAO consistent with:
Consistency with other probes
DESI Y1 BAO consistent with:
- SDSS (eBOSS Collaboration, 2020)
- primary CMB: Planck Collaboration, 2018 and CMB lensing: Planck PR4 + ACT DR6 lensing ACT Collaboration, 2023, Carron, Mirmelstein, Lewis, 2022
Consistency with other probes
DESI Y1 BAO consistent with:
- SDSS (eBOSS Collaboration, 2020)
- primary CMB: Planck Collaboration, 2018 and CMB lensing: Planck PR4 + ACT DR6 lensing ACT Collaboration, 2023, Carron, Mirmelstein, Lewis, 2022
\underbrace{
\Omega_\mathrm{m} = 0.3069 \pm 0.0050 \; \mathbf{(1.6\%)}
}_{\textstyle \text{\green{DESI + CMB}}}
- BAO constrains \( r_\mathrm{d}(\Omega_\mathrm{m} h^{2}, \Omega_\mathrm{b} h^{2}) h \)
Hubble constant
- BAO constrains \( r_\mathrm{d}(\blue{\Omega_\mathrm{m}} h^{2}, \Omega_\mathrm{b} h^{2}) h \)
- \( \blue{\Omega_\mathrm{m}} \) constrained by BAO at different \(z\)
Hubble constant
- BAO constrains \( r_\mathrm{d}(\blue{\Omega_\mathrm{m}} h^{2}, \orange{\Omega_\mathrm{b} h^{2}}) h \)
- \( \blue{\Omega_\mathrm{m}} \) constrained by BAO at different \(z\)
- \(\orange{\Omega_\mathrm{b}h^2}\) can be constrained by BBN: Schöneberg et al., 2024
Hubble constant
- BAO constrains \( r_\mathrm{d}(\blue{\Omega_\mathrm{m}} h^{2}, \orange{\Omega_\mathrm{b} h^{2}}) h \)
- \( \blue{\Omega_\mathrm{m}} \) constrained by BAO at different \(z\)
- \(\orange{\Omega_\mathrm{b}h^2}\) can be constrained by BBN: Schöneberg et al., 2024
\(\implies\) constraints on \(h\) i.e. \(H_0\)
Hubble constant
\underbrace{
H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
Hubble constant
\underbrace{
H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}
\(\theta_\ast\) CMB angular acoustic scale
- Consistency with SDSS
\underbrace{
H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
Hubble constant
\underbrace{
H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}
- Consistency with SDSS
- In agreement with CMB
\underbrace{
H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
Hubble constant
\underbrace{
H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}
- Consistency with SDSS
- In agreement with CMB
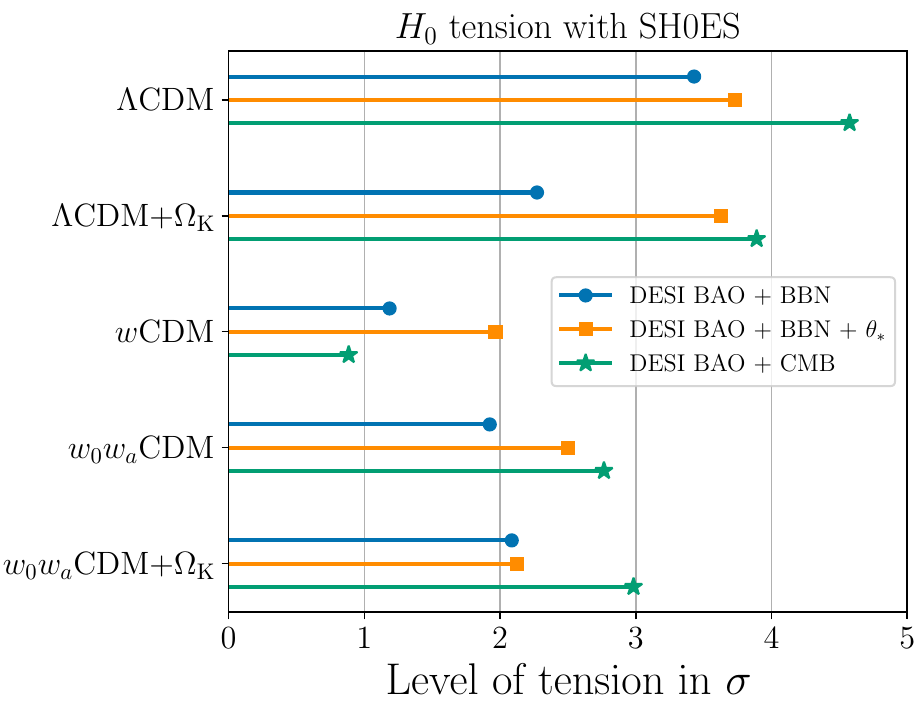
- In \(3.7 \sigma\) tension with SH0ES
\underbrace{
H_0 = (68.53 \pm 0.80) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \text{BBN}}}
Hubble constant
\underbrace{
H_0 = (68.52 \pm 0.62) \, {\rm km\,s^{-1}\,Mpc^{-1}}
}_{\textstyle \color{darkblue}{\text{DESI} + \theta_\ast + \text{BBN}}}
DESI + CMB measurements favor a flat Universe
\Omega_\mathrm{K} = 0.0024 \pm 0.0016 \; \green{(\text{DESI} + \text{CMB})}
Spatial curvature
Dark Energy Equation of State
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w\)
Dark Energy Equation of State
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w\)
Dark Energy Equation of State
SNe:
- Pantheon+ Brout, Scolnic, Popovic et al., 2022
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w\)
Dark Energy Equation of State
SNe:
- Pantheon+ Brout, Scolnic, Popovic et al., 2022
- Union3 Rubin, Aldering, Betoule et al. 2023
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w\)
Dark Energy Equation of State
SNe:
- Pantheon+ Brout, Scolnic, Popovic et al., 2022
- Union3 Rubin, Aldering, Betoule et al. 2023
- DES-SN5YR DES Collaboration et al. 2024
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w\)
Dark Energy Equation of State
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.3095 \pm 0.0065 & \mathbf{(2.1\%)} \\
w &= -0.997 \pm 0.025 & \mathbf{(2.5\%)}
\end{align*}}_{\textstyle \text{\color{orange}{DESI + CMB + Pantheon+}}}
Assuming a constant EoS, DESI BAO fully compatible with a cosmological constant...
\underbrace{\begin{align*}
\Omega_\mathrm{m} &= 0.293 \pm 0.015 & \mathbf{(5.1\%)} \\
w &= -0.99^{+0.15}_{-0.13} & \mathbf{(15\%)}
\end{align*}}_{\textstyle \text{\color{darkblue}{DESI}}}
Constant EoS parameter \(w\)
w(a) = w_{0} + (1 - a) w_{a} \qquad \text{(CPL)}
\left.
\begin{align*}
w_{0} &= -0.55^{+0.39}_{-0.21} \\
w_{a} &< -1.32
\end{align*}
\right\rbrace {\text{\color{black}{DESI}}}
Dark Energy Equation of State
Varying EoS
\Lambda
Dark Energy Equation of State
\underbrace{
w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00}
}_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}
w(a) = w_{0} + (1 - a) w_{a} \qquad \text{(CPL)}
Varying EoS
Dark Energy Equation of State
\underbrace{
w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00}
}_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}
w(a) = w_{0} + (1 - a) w_{a} \qquad \text{(CPL)}
Varying EoS
Dark Energy Equation of State
\underbrace{
w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00}
}_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}
w(a) = w_{0} + (1 - a) w_{a} \qquad \text{(CPL)}
Varying EoS
Dark Energy Equation of State
\underbrace{
w_{0} = -0.45^{+0.34}_{-0.21} \qquad w_{a} = -1.79^{+0.48}_{-1.00}
}_{\textstyle \purple{\text{DESI + CMB} \; \implies \; 2.6\sigma}}
w(a) = w_{0} + (1 - a) w_{a} \qquad \text{(CPL)}
Varying EoS
Dark Energy Equation of State
Combining all DESI + CMB + SN
\underbrace{
w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25}
}_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
Dark Energy Equation of State
Combining all DESI + CMB + SN
\underbrace{
w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25}
}_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
\underbrace{
w_{0} = -0.64 \pm 0.11\qquad w_{a} = -1.27^{+0.40}_{-0.34}
}_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.5\sigma}}
Dark Energy Equation of State
Combining all DESI + CMB + SN
\underbrace{
w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25}
}_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
\underbrace{
w_{0} = -0.64 \pm 0.11\qquad w_{a} = -1.27^{+0.40}_{-0.34}
}_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.5\sigma}}
\underbrace{
w_{0} = -0.727 \pm 0.067 \qquad w_{a} = -1.05^{+0.31}_{-0.27}
}_{\textstyle \color{green}{\text{DESI + CMB + DES-SN5YR} \; \implies \; 3.9\sigma}}
Dark Energy Equation of State
Combining all DESI + CMB + SN
\(w_{0} > -1, w_{a} < 0\) favored, level varying on the SN dataset
\underbrace{
w_{0} = -0.827 \pm 0.063 \qquad w_{a} = -0.75^{+0.29}_{-0.25}
}_{\textstyle \blue{\text{DESI + CMB + Pantheon+} \; \implies \; 2.5\sigma}}
\underbrace{
w_{0} = -0.64 \pm 0.11\qquad w_{a} = -1.27^{+0.40}_{-0.34}
}_{\textstyle \color{orange}{\text{DESI + CMB + Union3} \; \implies \; 3.5\sigma}}
\underbrace{
w_{0} = -0.727 \pm 0.067 \qquad w_{a} = -1.05^{+0.31}_{-0.27}
}_{\textstyle \color{green}{\text{DESI + CMB + DES-SN5YR} \; \implies \; 3.9\sigma}}
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
Sum of neutrino masses
Internal CMB degeneracies limiting precision on the sum of neutrino masses
Broken by BAO, especially through \(H_{0}\)
Low preferred value of \(H_{0}\) yields
\(\sum m_\nu < 0.072 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}\)
Limit relaxed for extensions to \(\Lambda\mathrm{CDM}\)
\(\sum m_\nu < 0.195 \, \mathrm{eV}\) for \(w_0w_a\mathrm{CDM}\)
Neutrino mass hierarchies
\sum m_\nu < 0.113 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
With \(> 0.059 \, \mathrm{eV}\) prior (NH)
Neutrino mass hierarchies
\sum m_\nu < 0.113 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
\sum m_\nu < 0.145 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
With \(> 0.059 \, \mathrm{eV}\) prior (NH)
With \(> 0.1 \, \mathrm{eV}\) prior (IH)
Neutrino mass hierarchies
\sum m_\nu < 0.113 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
\sum m_\nu < 0.145 \, \mathrm{eV} \; (95\%, \color{green}{\text{DESI + CMB})}
With \(> 0.059 \, \mathrm{eV}\) prior (NH)
With \(> 0.1 \, \mathrm{eV}\) prior (IH)
Current constraints do not strongly favor normal over inverted hierarchy (\(\simeq 2 \sigma\))
Summary
DESI + BBN (+ \(\theta_\ast\)) constraints \(H_{0}\) to ~1%, tension w/ SH0ES
Summary
DESI + BBN (+ \(\theta_\ast\)) constraints \(H_{0}\) to ~1%, tension w/ SH0ES
DESI, in combination with CMB data, favors zero spatial curvature
Summary
DESI + BBN (+ \(\theta_\ast\)) constraints \(H_{0}\) to ~1%, tension w/ SH0ES
DESI, in combination with CMB data, favors zero spatial curvature
DESI is consistent with \(w = -1\) when assumed constant
When allowing \(w\) to vary, DESI combined with CMB: \(2.6 \sigma\) and SN: \(2.5\) to \(3.9 \sigma\) tension with \((w_{0}, w_{a}) = (-1, 0)\)
Summary
DESI + BBN (+ \(\theta_\ast\)) constraints \(H_{0}\) to ~1%, tension w/ SH0ES
DESI, in combination with CMB data, favors zero spatial curvature
DESI is consistent with \(w = -1\) when assumed constant
When allowing \(w\) to vary, DESI combined with CMB: \(2.6 \sigma\) and SN: \(2.5\) to \(3.9 \sigma\) tension with \((w_{0}, w_{a}) = (-1, 0)\)
Limit on \(\sum m_\nu\) improves to \(< 0.072 \, \mathrm{eV} \; (95\%, \Lambda\mathrm{CDM})\), \(< 0.195 \, \mathrm{eV} \; (95\%, w_{0}w_{a}\mathrm{CDM}) \)
Other datasets
- SDSS BAO (for comparisons only): eBOSS Collaboration, 2020
- Primary CMB: Planck Collaboration, 2018
- CMB lensing: Planck PR4 + ACT DR6 lensing ACT Collaboration, 2023, Carron, Mirmelstein, Lewis, 2022
- BBN: Schöneberg et al., 2024
- SN: Pantheon+ Brout, Scolnic, Popovic et al., 2022, Union3 Rubin, Aldering, Betoule et al. 2023, DES-SN5YR DES Collaboration
Hubble tension
\(w(z)\)
\(w(z)\)
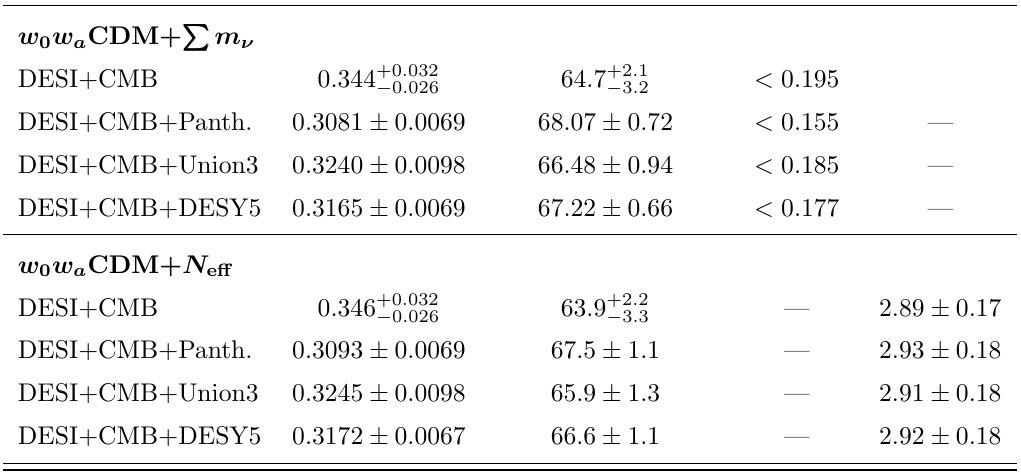
Full tables
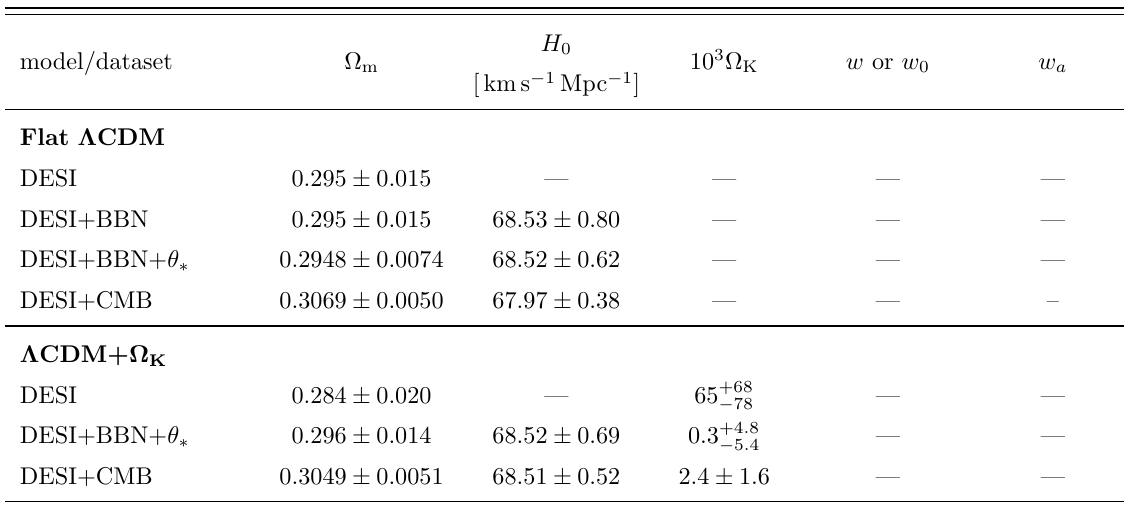
Full tables
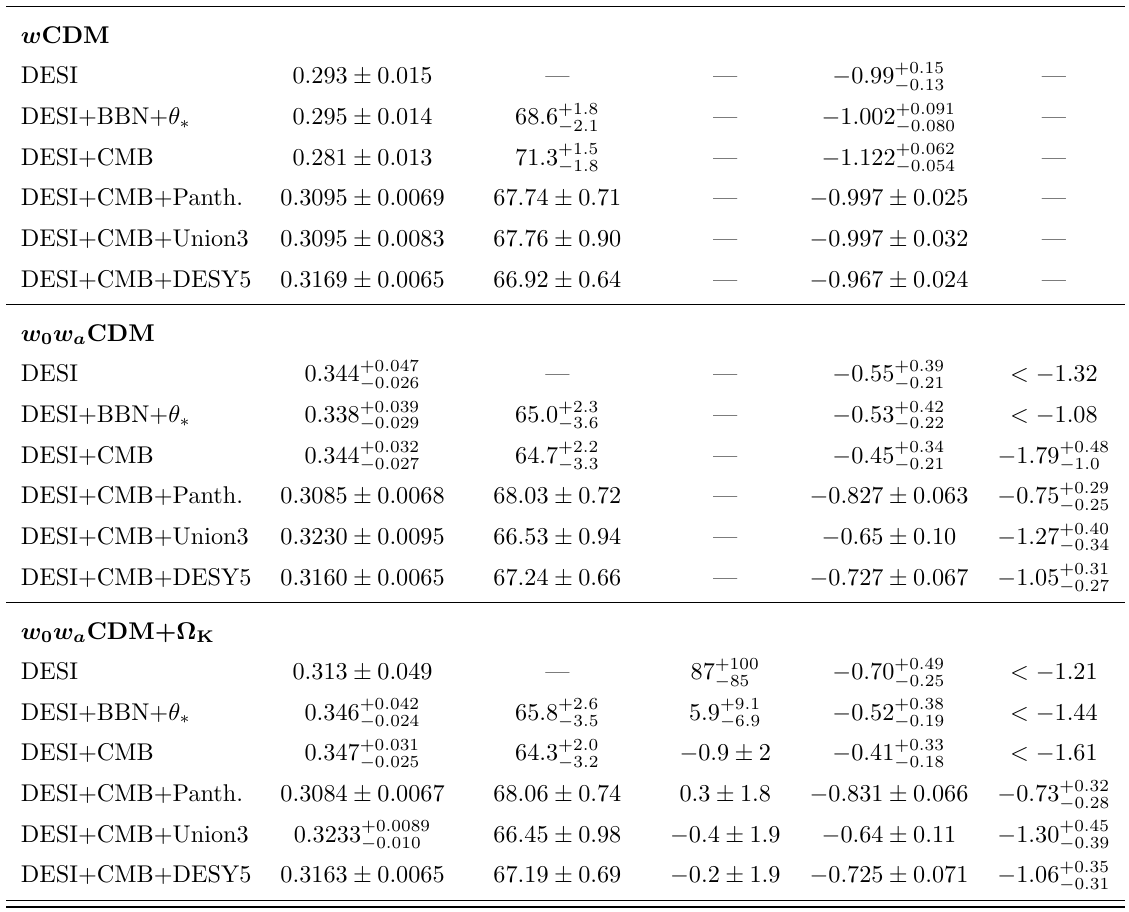
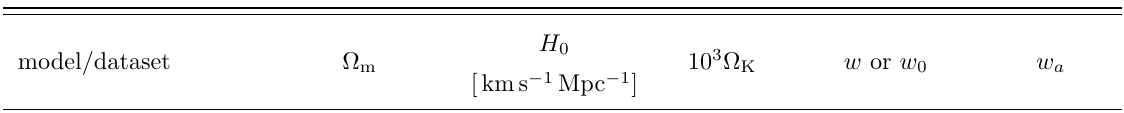
Full tables
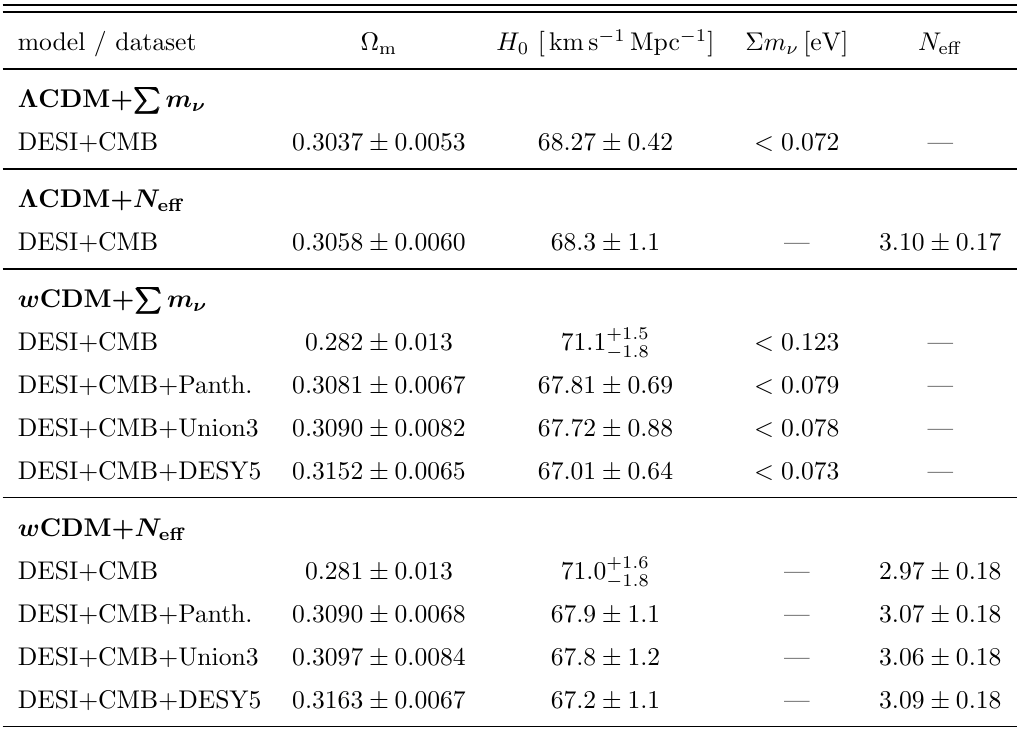
Full tables
Dark Energy Equation of State
Preference for \(w_{0} > -1, w_{a} < 0\) persists when curvature is left free
Moriond_April2024
By Arnaud De Mattia
