Differentiable

Agent-Based Models

Oxford, January 2024

Arnau Quera-Bofarull

www.arnau.ai

Modelling an epidemic

Two common approaches:

1. SIR models

\frac{dS}{dt} = -\frac{\beta S I}{N}
\frac{dI}{dt} = \frac{\beta SI}{N} - \gamma I
\frac{dR}{dt} = \gamma I

Pros:

"cheap",

simple,

...

Cons:

only models "averages",

...

Two common approaches:

2. ABM models

Pros:

individual agents,

individual interactions,

...

Cons:

computational cost,

calibration,

...

Modelling an epidemic

Calibration

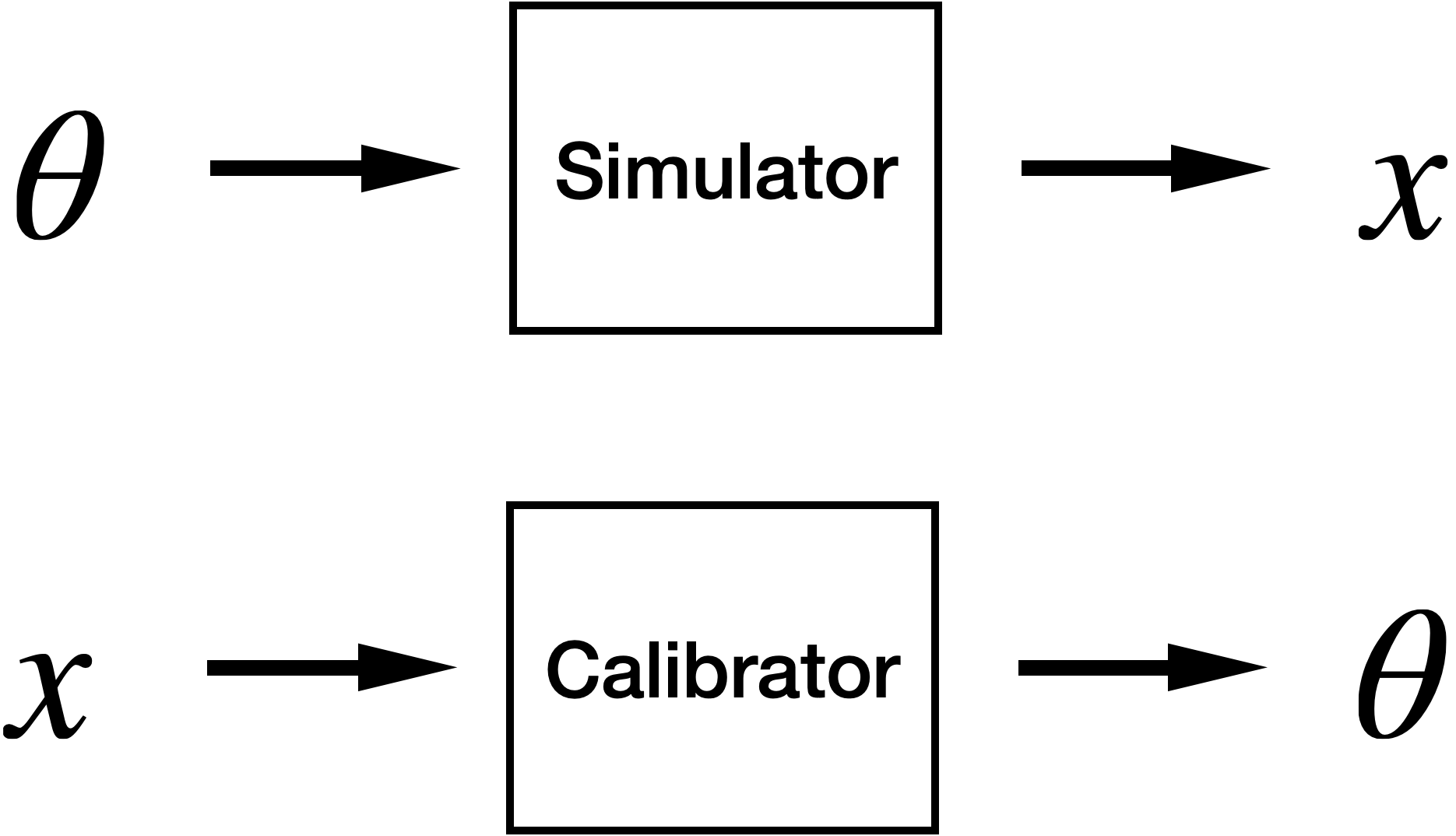
Typically hard because

  1. No access to the likelihood.
  2. Simulator is slow to run.
  3. Large parameter space.

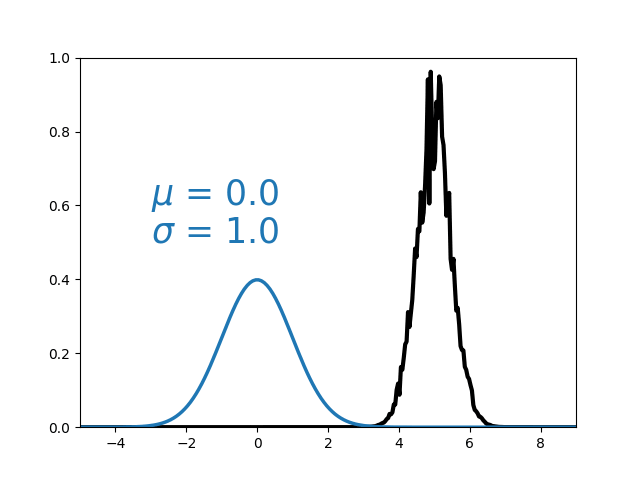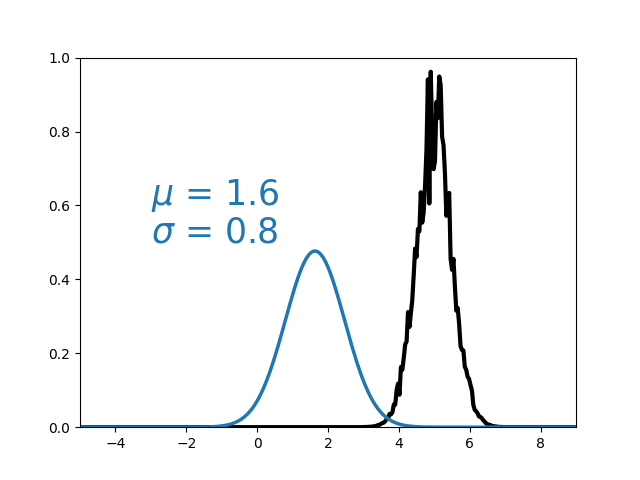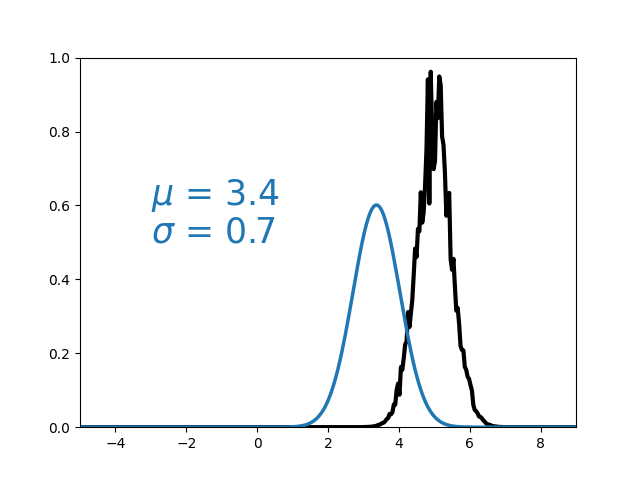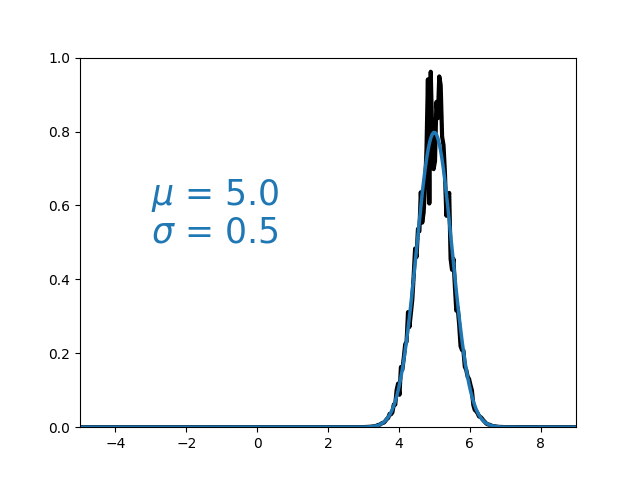
Variational Inference

  1. Assume posterior can be approximated by a parameterised distribution.

     
  2. Optimise for best parameters using gradient

(Generalized) Variational Inference

Knoblauch et al (2019)

\mathbf \theta
\mathbf y

ABM

\ell (\mathbf \theta, \mathbf y)
\pi(\mathbf \theta \mid \mathbf y) \propto e^{-\ell (\mathbf \theta, \mathbf y)}\pi(\mathbf\theta)

Prior

(Generalized) posterior

(Generalized) Variational Inference

\pi(\mathbf \theta \mid \mathbf y) \approx q^*(\mathbf \theta)

Optimization problem

Assume posterior approximated by variational family

q^*(\mathbf \theta) = \argmin_{q \in \mathcal Q}
q^*(\mathbf \theta) = \argmin_{q \in \mathcal Q} \left[ \mathbb E_{q(\mathbf \theta)} \ell(\mathbf \theta, \mathbf y) + D(q (\mathbf \theta) \mid \mid \pi(\mathbf \theta)) \right]
q^*(\mathbf \theta) = \argmin_{q \in \mathcal Q} \left[ \mathbb E_{q(\mathbf \theta)} \ell(\mathbf \theta, \mathbf y) \right .

Distance between ABM output and data

Divergence posterior - prior

How to optimize q?

q_{\phi^*}(\mathbf \theta) = \argmin_{\phi \in \Phi} \left[ \mathbb E_{q_\phi(\mathbf \theta)} \ell(\mathbf \theta, \mathbf y) + D(q_\phi (\mathbf \theta) \mid \mid \pi(\mathbf \theta)) \right]
\phi' \longrightarrow \phi' - \eta \nabla_\phi \mathcal L(\phi')

Choose parametric family of distributions (e.g., Normal)

q(\mathbf \theta) = q_\phi (\mathbf \theta)
q_{\mathbf \phi} (\mathbf \theta) = \frac{1}{\mathbf\phi_2\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{\mathbf\theta - \mathbf\phi_1}{\mathbf \phi_2}\right)^2}

How to optimize q?

\nabla_\phi \mathbb E_{\theta \sim q_\phi(\mathbf \theta)} \ell(\mathbf \theta, \mathbf y)

Need to compute the gradient

\mathbb E_{\theta \sim q_\phi(\mathbf \theta)} \left[\nabla_\phi \log q_\phi(\mathbf\theta) \cdot \ell(\mathbf\theta, \mathbf y)\right]

Score function estimator

Monte Carlo

gradient estimation

Mohamed et al (2020)

\mathbb E_{\epsilon \sim q_\phi(\epsilon)} \left[\nabla_\phi \ell(f(\epsilon; \mathbf\theta, \mathbf y))\right]

Path-wise estimator

Reparameterization

Score function estimator

Path-wise estimator

  • Unbiased
  • Typically high variance
  • Does not require differentiable simulator
  • Unbiased*
  • Low(er) variance
  • Requires differentiable simulator

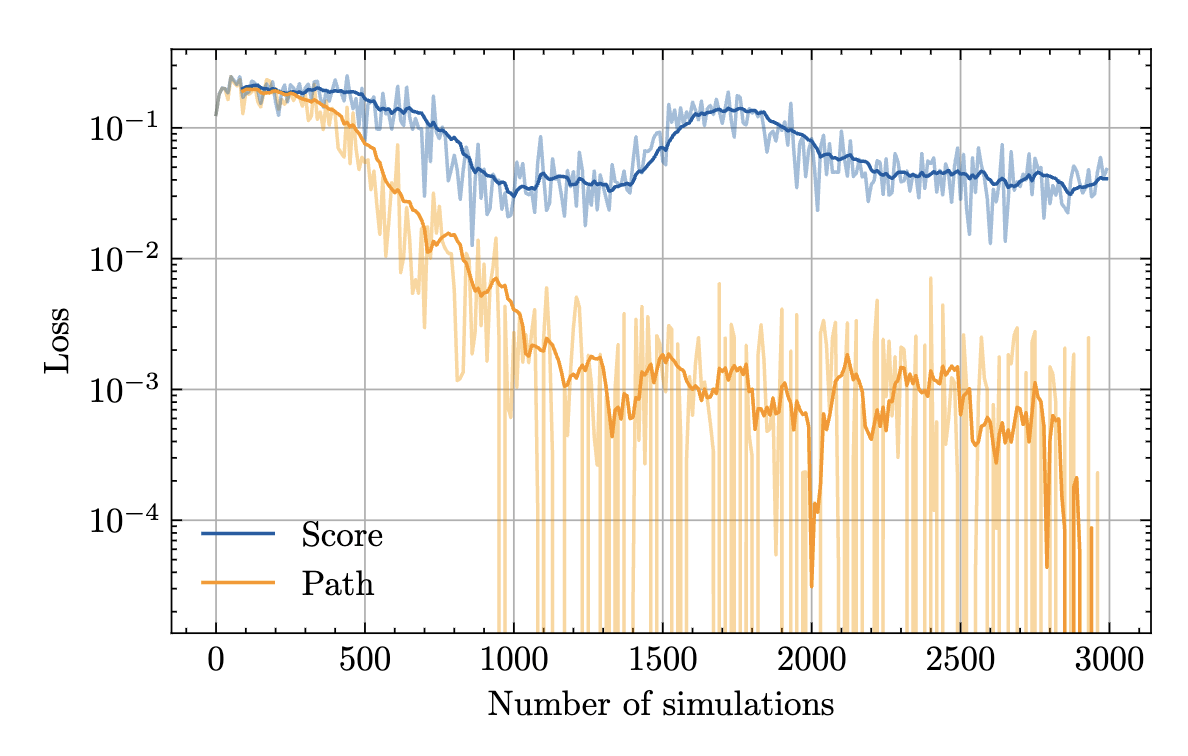
"Gradient assisted calibration of financial agent-based models" Dyer et al. (2023)

How to build differentiable
Agent-Based Models

Differentiable simulators

f: \mathbb R^m \longrightarrow \mathbb R^n
(J_f)_{ij} = \frac{\partial f_i}{\partial x_j}

Numerical differentiation

\frac{\partial f}{\partial x} = \lim_{\epsilon \to 0}\frac{f(x+\epsilon) - f(x)}{\epsilon}

Inaccurate

Automatic differentiation

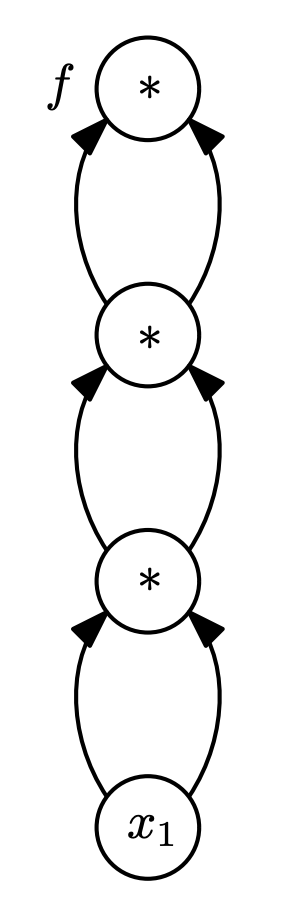
def f(x1)
	t1 = x1 * x1
    t2 = t1 * t1
    return t2 * t2
t_1
t_2

2

4

16

256

\frac{\partial f}{\partial t_2} = 2 t_2 = 2 \cdot 16 = 32
f
x_1
\frac{\partial t_2}{\partial t_1} = 2 t_1 = 2 \cdot 4 = 8
\frac{\partial t_1}{\partial x_1} = 2 x_1 = 2 \cdot 2 = 4
\frac{\partial f}{\partial f} = 1
f'(x) = 8x^7 = 8\cdot 2^7 = 1024 = 32 \cdot 8 \cdot 4

Idea:

Decompose program into basic operations that we can differentiate

Automatic differentiation

Reverse mode AD

t_1
t_2

2

4

16

256

\frac{\partial f}{\partial t_2} = 32
f
x_1
\frac{\partial t_2}{\partial t_1} = 8
\frac{\partial t_1}{\partial x_1} = 4

Forward mode AD

\frac{\partial x_1}{\partial x_1} = 1
t_1
t_2

2

4

16

256

\frac{\partial f}{\partial t_2} = 32
f
x_1
\frac{\partial t_2}{\partial t_1} = 8
\frac{\partial t_1}{\partial x_1} = 4
\frac{\partial f}{\partial f} = 1

Automatic differentiation

Reverse mode AD

t_1
t_2

2

4

16

256

\frac{\partial f}{\partial t_2} = 32
f
x_1
\frac{\partial t_2}{\partial t_1} = 8
\frac{\partial t_1}{\partial x_1} = 4

Forward mode AD

\frac{\partial x_1}{\partial x_1} = 1
t_1
t_2

2

4

16

256

\frac{\partial f}{\partial t_2} = 32
f
x_1
\frac{\partial t_2}{\partial t_1} = 8
\frac{\partial t_1}{\partial x_1} = 4
\frac{\partial f}{\partial f} = 1

Forward vs Reverse

Multiple outputs

def f(x1)
	t1 = x1 * x1
    t2 = t1 * t1
    return [t2, t2, t2]

Reverse needs 3 full model evaluations!

Forward can amortize

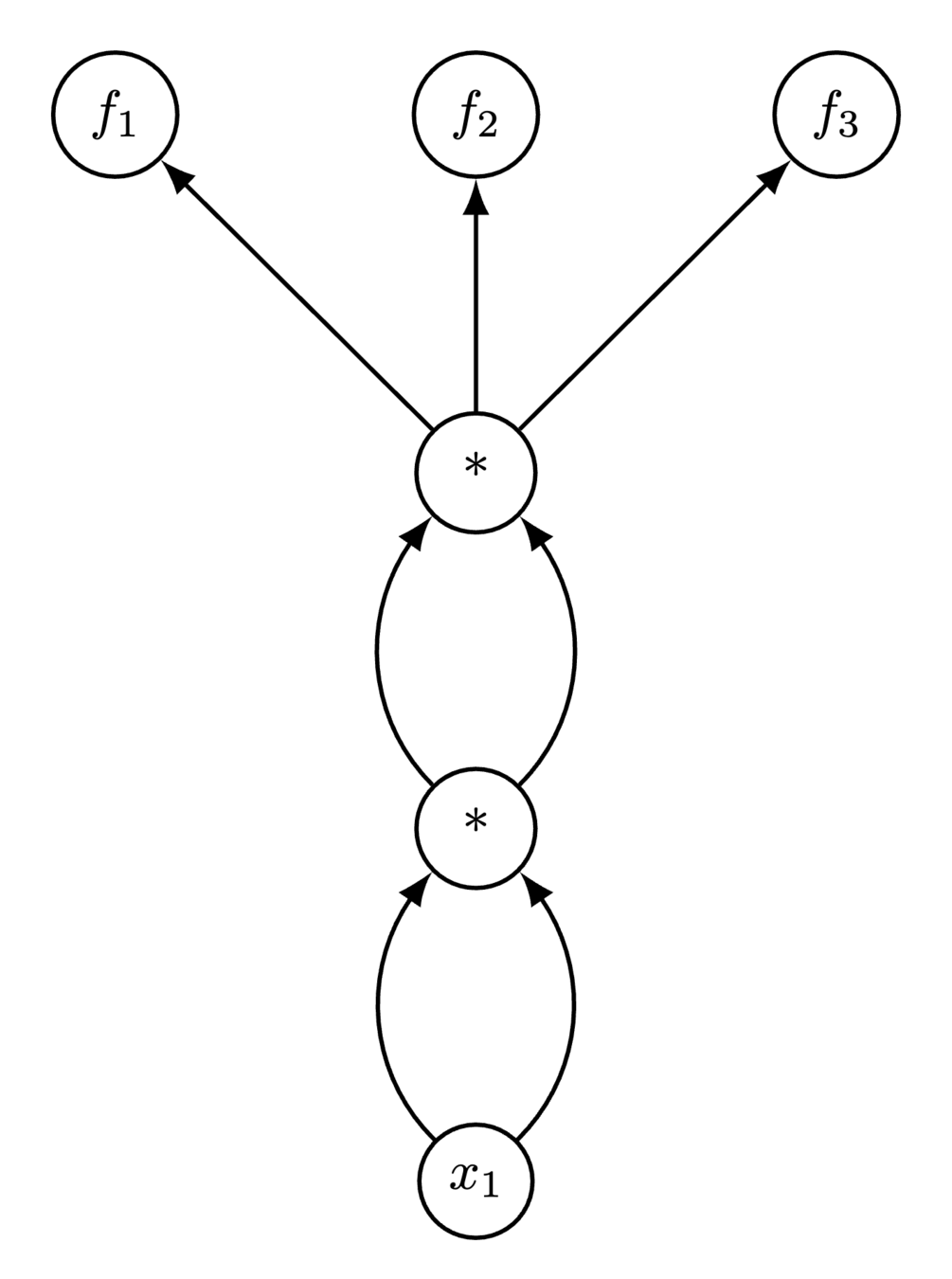
Forward vs Reverse

Multiple inputs

def f(x1, x2, x3)
	t1 = x1 * x2 * x3
    t2 = t1 * t1
    return t2 * t2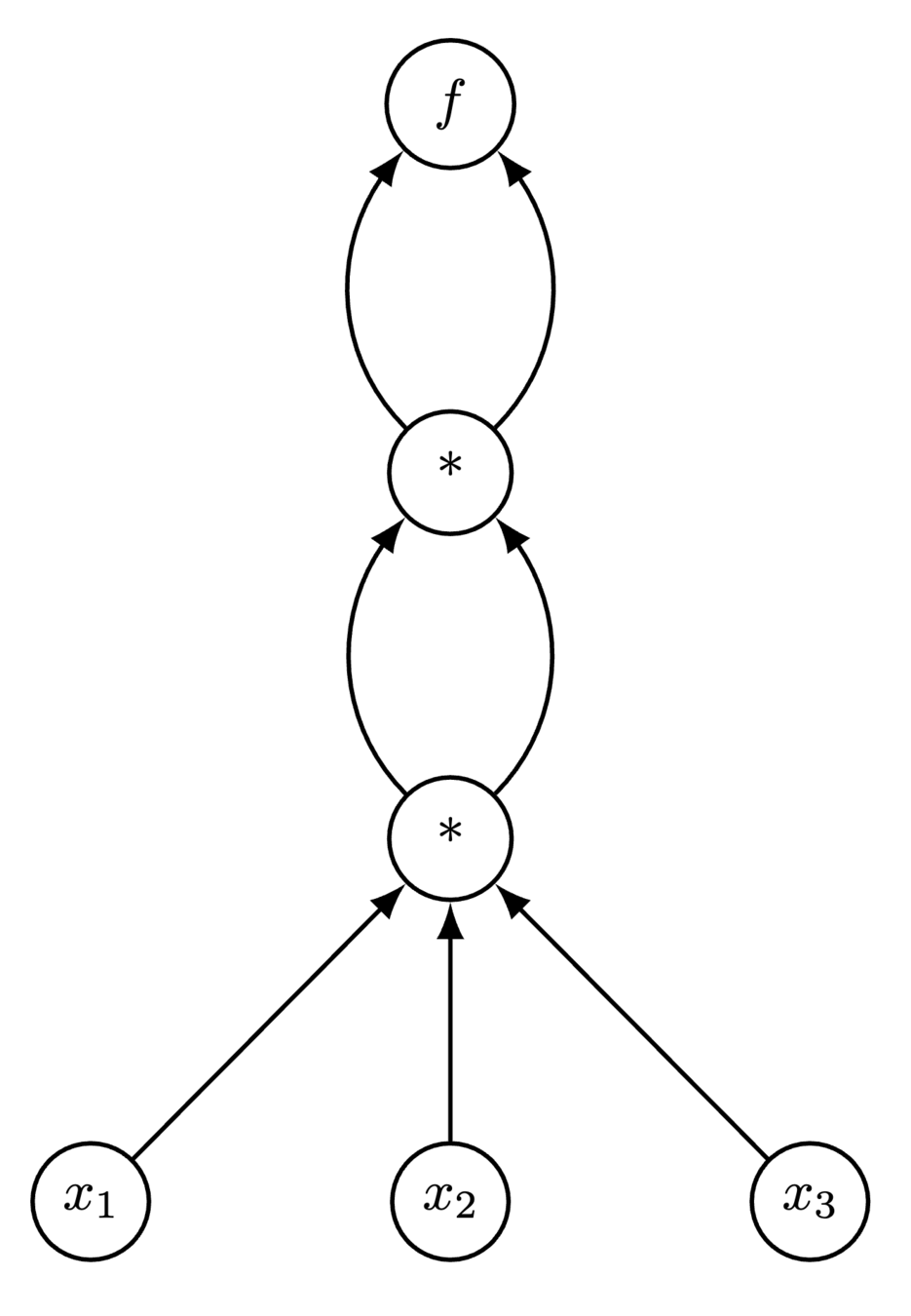

Forward needs 3 full model evaluations!

Reverse can amortize

Forward vs Reverse

f: \mathbb R^m \longrightarrow \mathbb R^n

Reverse mode preferred for deep learning

m \gg n

However

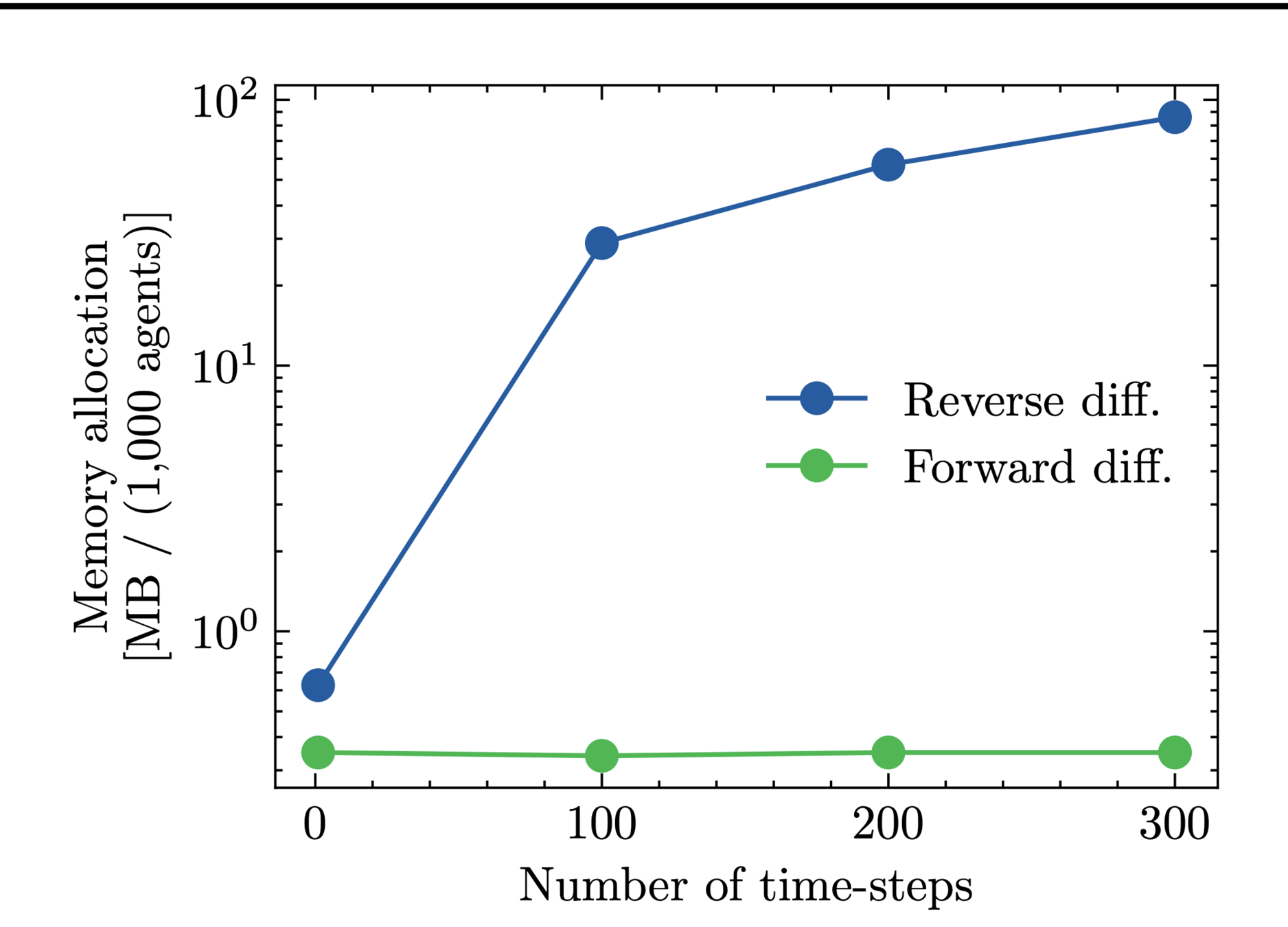
Quera-Bofarull et al. "Some challenges of calibrating differentiable agent-based models"

Reverse mode needs to store computational graph!

 

Can blow up in memory

Differentiating through randomness

x \sim \mathcal N(\mu, \sigma^2)
\epsilon \sim \mathcal N(0, 1)
x = \mu + \epsilon \sigma
\frac{\mathrm{d} x}{\mathrm{d} \mu} = 1
\frac{\mathrm{d} x}{\mathrm{d} \sigma} = \epsilon

What about discrete distributions?

x \sim \mathrm{Categorical}(\mathbf p)

Option 1: Straight-Through

Just assign a gradient of 1.

 

Works if program is linear

Bengio et al. (2013)

x \sim \mathrm{Categorical}(\mathbf p)

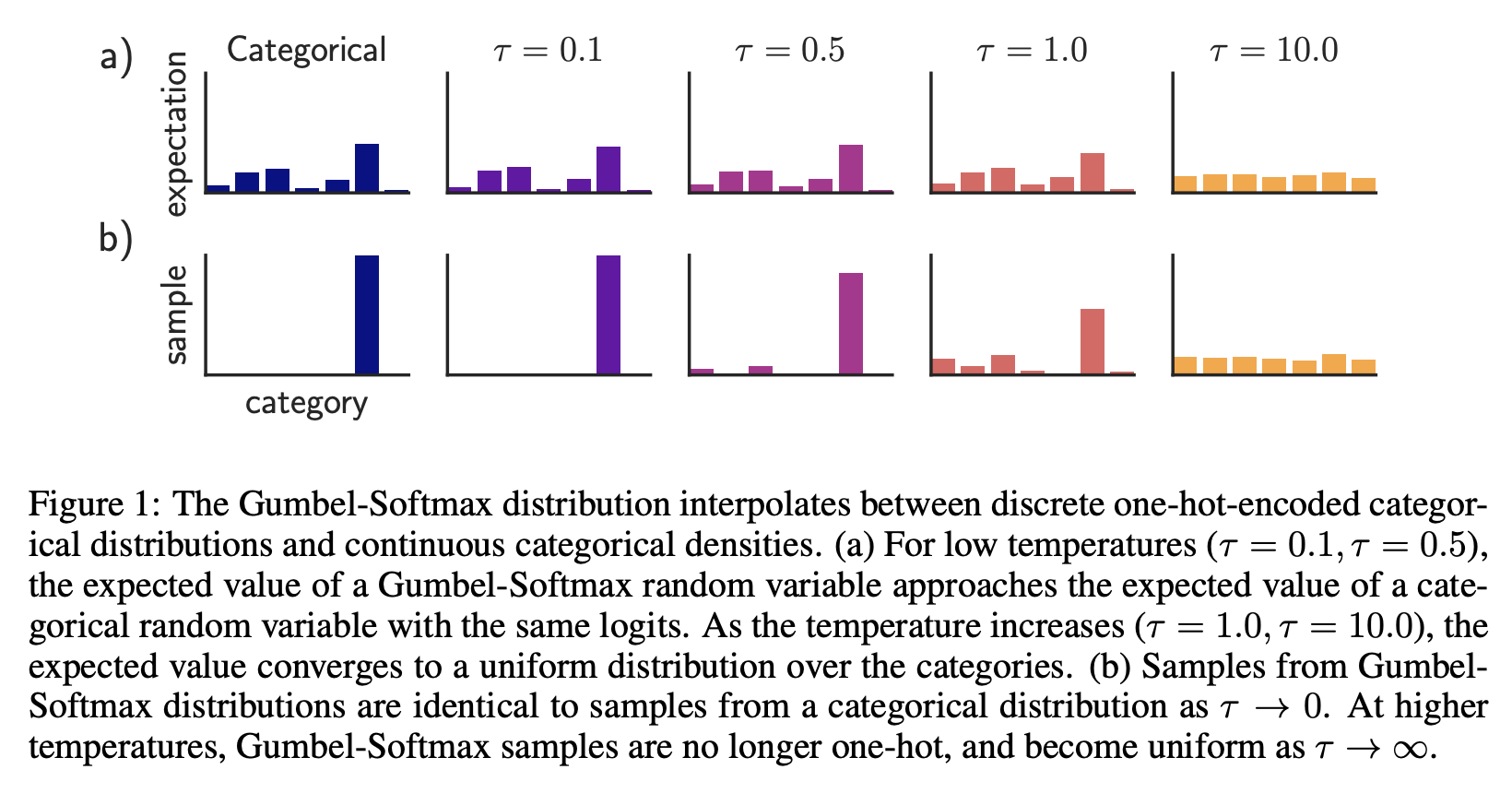
Option 2: Gumbel-Softmax

Jang et al. (2016)

Bias vs Variance tradeoff

x \sim \mathrm{Categorical}(\mathbf p)

Option 3: Smooth Perturbation analysis

StochaticAD.jl -- Arya et al. (2022)

Unbiased!

So does it work?

arnau.ai/blackbirds

Multiple examples of differentiable ABMs in PyTorch and Julia

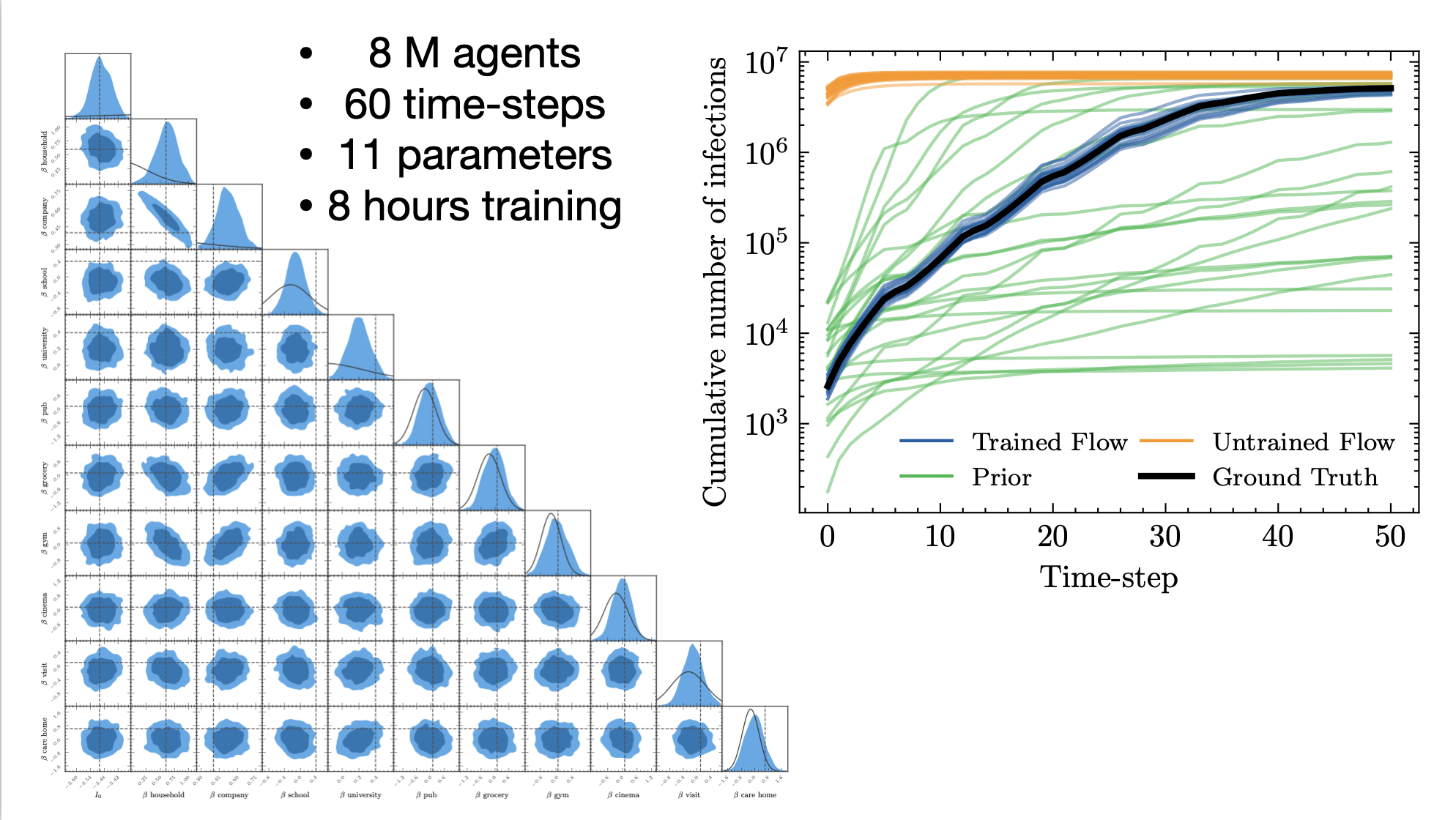
JUNE epidemiological model

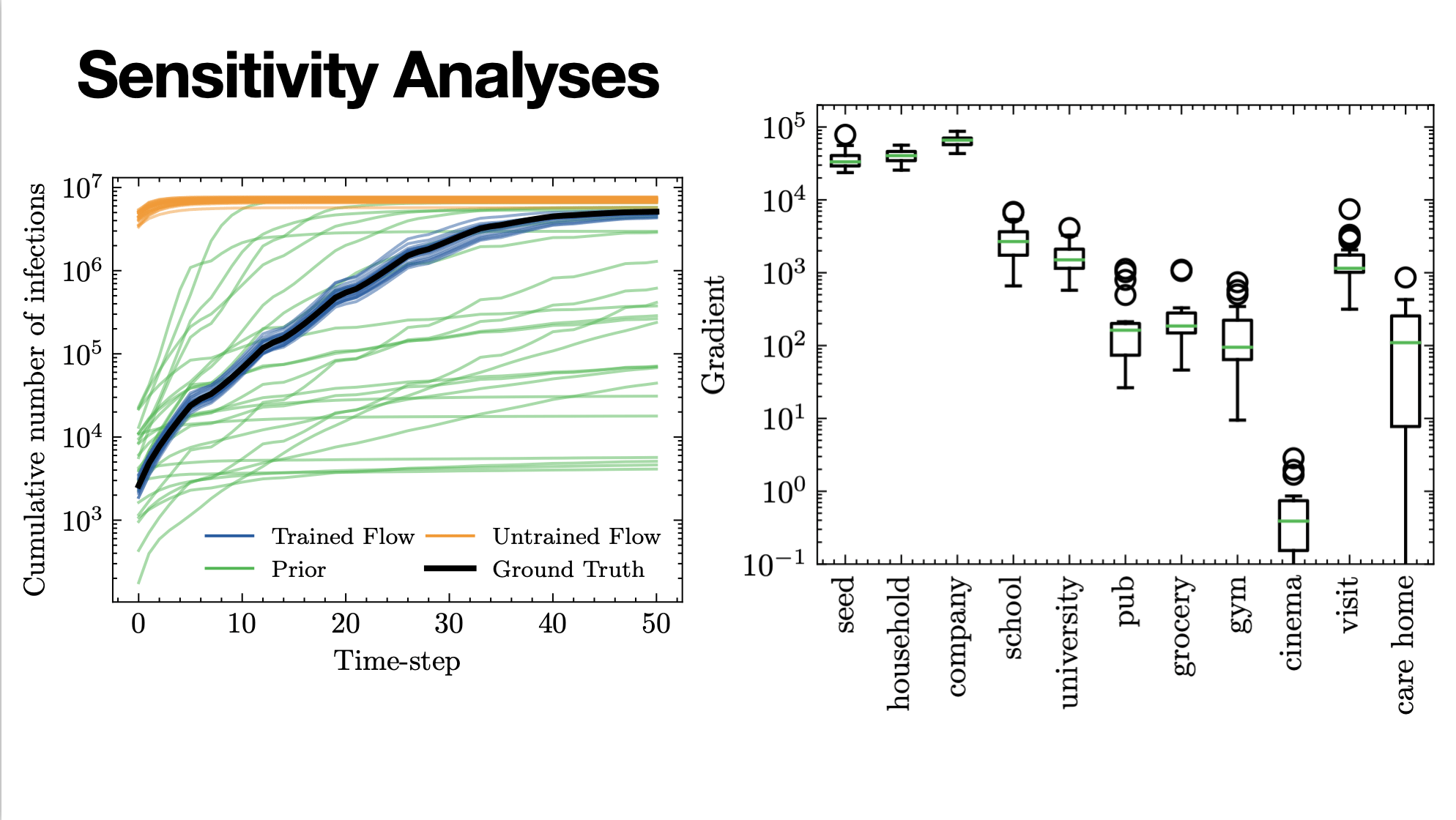
Reverse-mode gives us senstivity analysis for free

Summary

  1. Generalized Variational Inference promising route to calibrate differentiable ABMs.

  2. Differentiable ABMs can be built using Automatic Differentiation

  3. Automatic Differentiation provides O(1) sensitivity analysis.

Slides and papers:

www.arnau.ai/talks

Diff ABM examples:

www.arnau.ai/blackbirds

Backup slides

Symbolic differentiation

function f(x1)
	t1 = x1 * x1
    t2 = t1 * t1
    return t2 * t2
end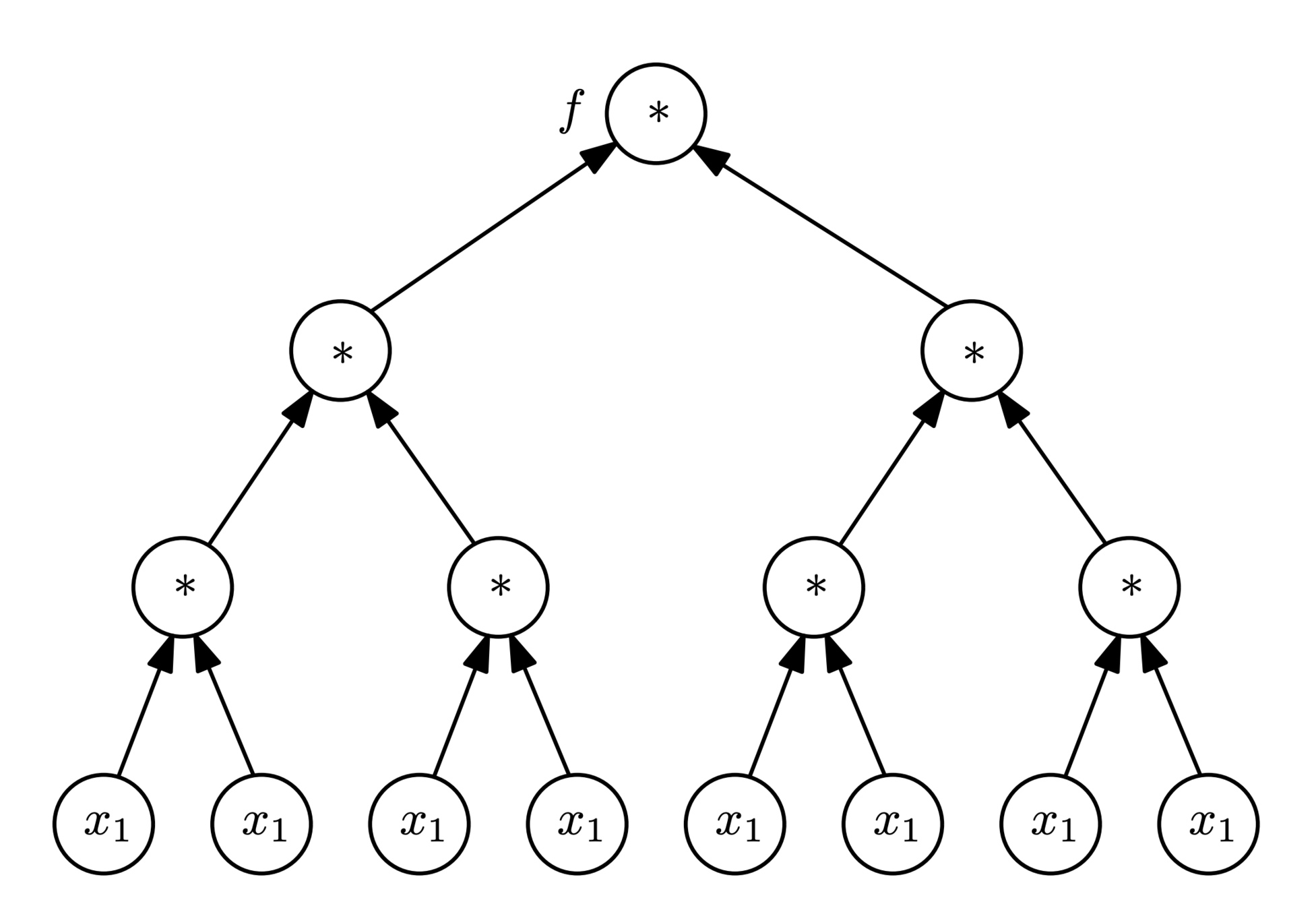
f(x) = x^8

Symbolic differentiation

Hard-code calculus 101 derivatives

\begin{align*} x' &= 1\\ (f+g)' &= f' + g'\\ (fg)' &= f'g + fg'\\ \end{align*}

Recurrently go down the tree via chain rule

Inefficient representation

Exact result

Automatic differentiation

DifferentiableAgent-Based Models

By arnauqb

Made with Slides.com

DifferentiableAgent-Based Models

  • 192

More from arnauqb