Занятие №8:
Космические скорости
Закон сохренения энергии
Закон сохранения полной механической энергии
E = K + U
= \dfrac{mv^{2}}{2} - \dfrac{GMm}{r}
> 0
Закон сохранения полной механической энергии
E = K + U
= \dfrac{mv^{2}}{2} - \dfrac{GMm}{r}
= 0
Закон сохранения полной механической энергии
E = K + U
= \dfrac{mv^{2}}{2} - \dfrac{GMm}{r}
< 0
E = 0
r
ЦГТ
K + U = 0
\dfrac{mv^{2}}{2}-\dfrac{GMm}{r}=0
\dfrac{v^{2}}{2}=\dfrac{GM}{r}
v_{p}=\sqrt{\dfrac{2GM}{r}}
v_{2к}=\sqrt{\dfrac{2GM}{R}}
v_{2к\oplus}=11.2 \: \: км/c
параболическая скорость
r=R+h
R
0
v_{p}
v_{2к}
E < 0
K + U = - \left | E \right |
E = - \left | E \right |
\dfrac{mv^{2}}{2}-\dfrac{GMm}{r}=- \left | E \right |
\dfrac{mv^{2}}{2}=\dfrac{GMm}{r}- \left | E \right |
v^{2} = \dfrac{2GM}{r} - \dfrac{2\left | E \right |}{m}
= GM \left ( \dfrac{2}{r}-\dfrac{2\left | E \right |}{GMm}\right )
=\dfrac{1}{a}
\dfrac{2\left | E \right |}{GMm}=\dfrac{1}{a}
по теореме Вириала!
v^{2}=GM \left ( \dfrac{2}{r}-\dfrac{1}{a} \right )
v_{e}=\sqrt{GM\left (\dfrac{2}{r}-\dfrac{1}{a} \right )}
эллиптическая скорость
E < 0
a=r
r
ЦГТ
v_{c}
v_{1к}
v_{e}=\sqrt{GM\left (\dfrac{2}{r}-\dfrac{1}{a} \right )}
v_{c}=\sqrt{\dfrac{GM}{r}}
v_{1к}=\sqrt{\dfrac{GM}{R}}
круговая скорость
v_{1к\oplus}=7.8 \: \: км/c
r=R+h
R
0
E > 0
E = \left | E \right |
K + U = \left | E \right |
v^{2} = \dfrac{2GM}{r} + \dfrac{2\left | E \right |}{m}
v = \sqrt{\dfrac{2GM}{r} + \dfrac{2\left | E \right |}{m}}
гиперболическая скорость
Физика + Математика = 💙
v_{c}
\leftrightarrow
e_{c}=0
<
>
=
v_{e}
\leftrightarrow
<
e_{e}\in (0,1)
<
<
v_{p}
\leftrightarrow
e_{p}=1
<
<
v_{h}
\leftrightarrow
e_{h}>1
<
<
v_{L} = \infty
\leftrightarrow
e_{L} = \infty
так нельзя, поскольку ничего не может двигаться быстрее скорости света!
ничего во Вселенной не может двигаться по прямым линиям
свет так же искривляется вблизи тяготеющего центра
Искривление луча света вблизи ЦГТ
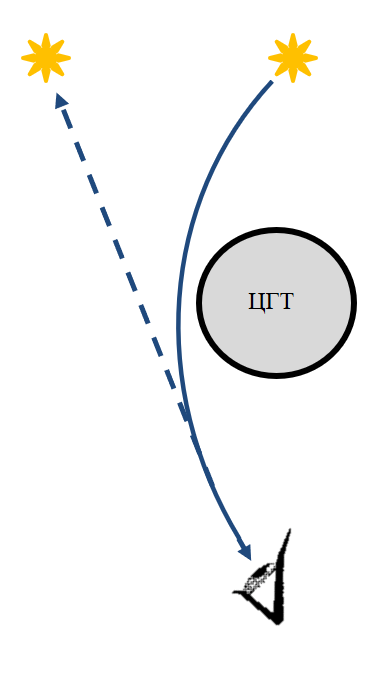
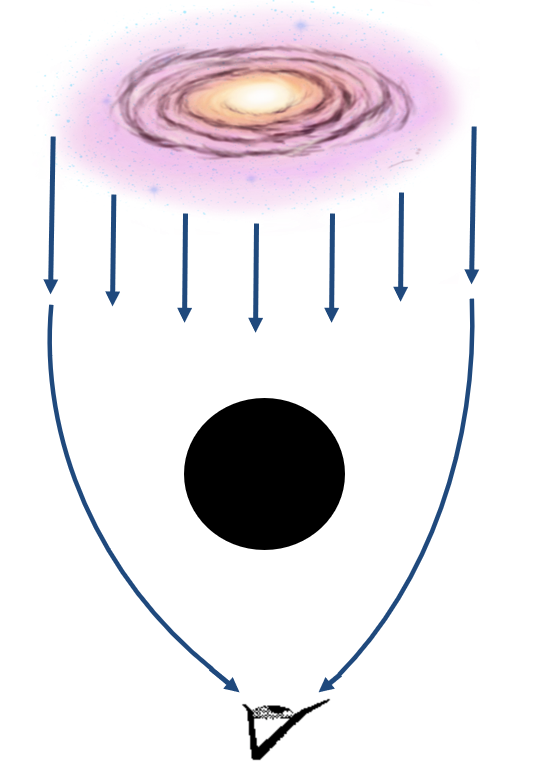
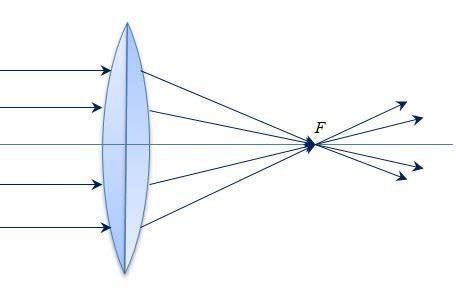
Гравитационная линза
Гравитационное линзирование
Гравитационное линзирование
Гравитационное линзирование
Жизнь звезд
Строение вещества
T\downarrow
T\downarrow
T\uparrow
T\uparrow
T\uparrow
Формирование звезд
Газо-пылевое облако
Остывание и сжатие
Формирование идеальной сферы
T\uparrow
=>
P\uparrow
T\uparrow\uparrow
=>
P\uparrow\uparrow
Термоядерные реакции
Жизнь звезд
F_G
F_L
Сила лучистого давления
F_G
F_L
=
Звезда живет!
\varepsilon
Свет, излучённый с поверхности звезды
T\downarrow
Ядро звезды
H_1^1
H_1^1
+
He_4^2
\rightarrow
\varepsilon
T_\text{ядра}
\sim
10^6 \, \text{K}
T_\text{eff}
\sim
10^3 \, \text{K}
Смерть звезд
Начало конца
F_G
F_L
>
Внешние слои звезды расширяются
H_1^1
Окрестности ядра начинают «падать» на ядро
Возникают ударные волны, распространяющиеся к поверхности звезды
Наступает стадия красного гиганта
Близится веселье!
Смерть звезды массы ~M⊙
Внешние слои разлетаются
Белый карлик
Планетарная туманность
Расширение продолжается
Оголяется ядро
Белый карлик
Hubble Space Telescope image
Sirius A
Sirius B
A Chandra X-ray Observatory image
Sirius B
Sirius A
R_{\text{БК}}
R_{\oplus}
\sim
Планетарная туманность
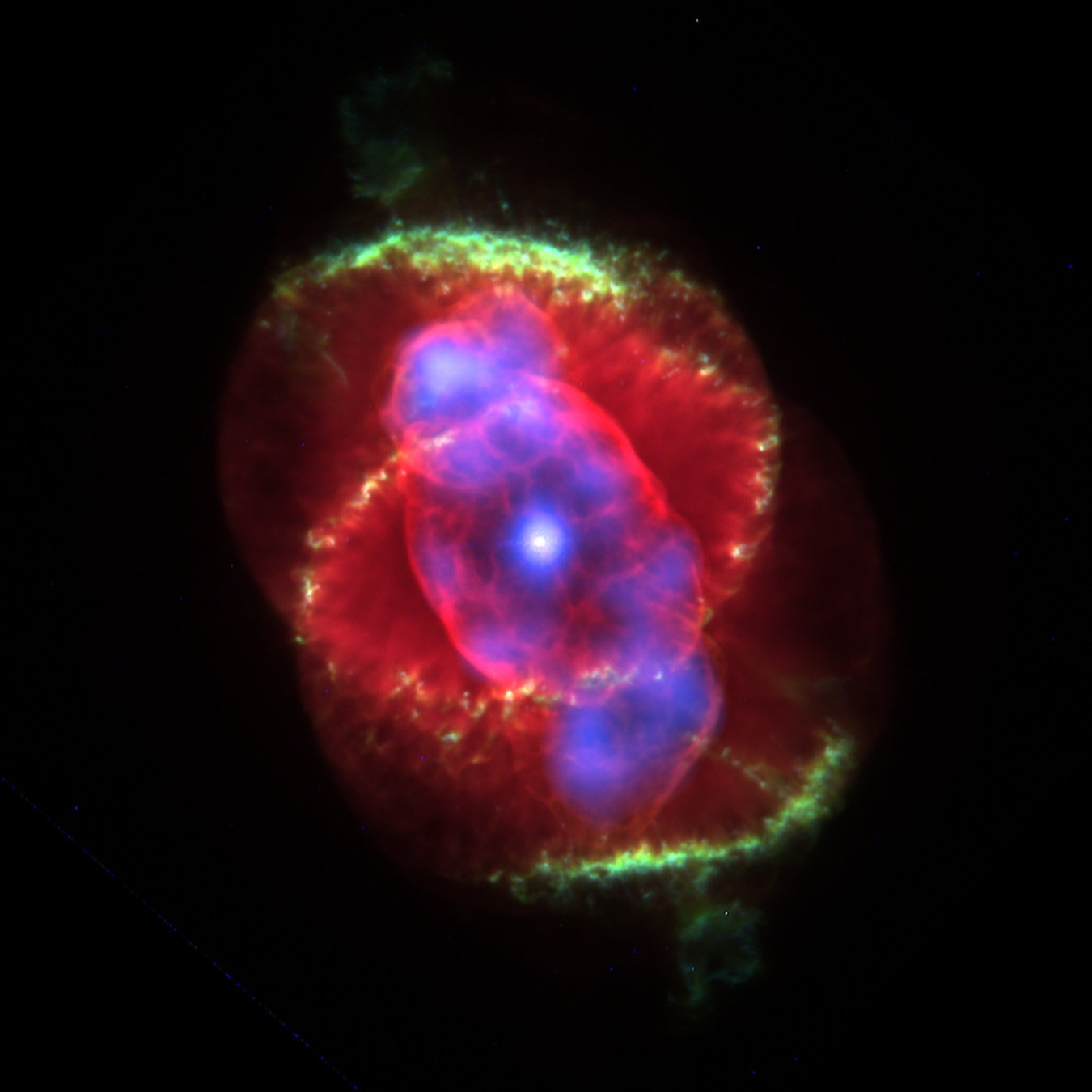
Смерть звезды с массой ядра >1.4·M⊙
Вещество в ядре сильно уплотняется
Т. к. звезда большая
Внешние слои начинают падать на ядро
Остатки сверхновой
F_G
F_L
\gg
Сверхсильные ударные волны
Сверхновая звезда
=
Нейтронная звезда
Нейтронная материя
Нейтрон
Обратный β-распад
\oplus
\ominus
Нейтронная звзезда
R_{\text{БК}}
\sim
10 - 12 \text{км}
Остатки сверхновой
Смерть звезды с массой ядра~(2-3)·M⊙
Все аналогично звезде с массой >1.4·M⊙
R_{\text{КЗ}} \sim 6 - 10 \, \text{км}
Нейтрон
Нейтрон
Кварк
Кварковая материя
Кварковые звезды
Обратный β-распад
Деконфайнмент кварков
Смерть звезды с массой ядра >(2-3)·M⊙
Кварк
Кварк
ХАНА!!!
Все аналогично предыдущему случаю
Деконфайнмент кварков
E = mc^2
R_{\mu\nu} - \dfrac{1}{2}Rg_{\mu\nu} = \dfrac{8\pi G}{c^4}T_{\mu\nu}
Аналогично
\begin{cases}
x \\
x \\
x \\
y
\end{cases}
\begin{cases}
x \\
x \\
\end{cases}
Геометрия пространства-времени
Материя - энергия
Двумерная аналогия
Динамика ОТО
Модель двумерной черной дыры
Трехмерное искривление пространства-времени
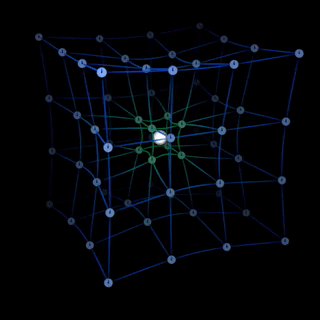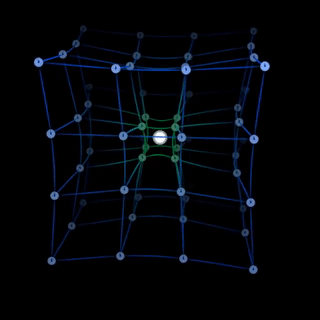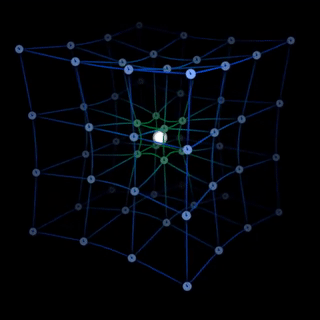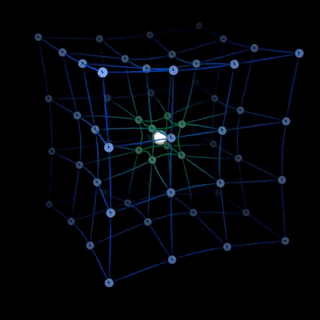
Трехмерная черная дыра
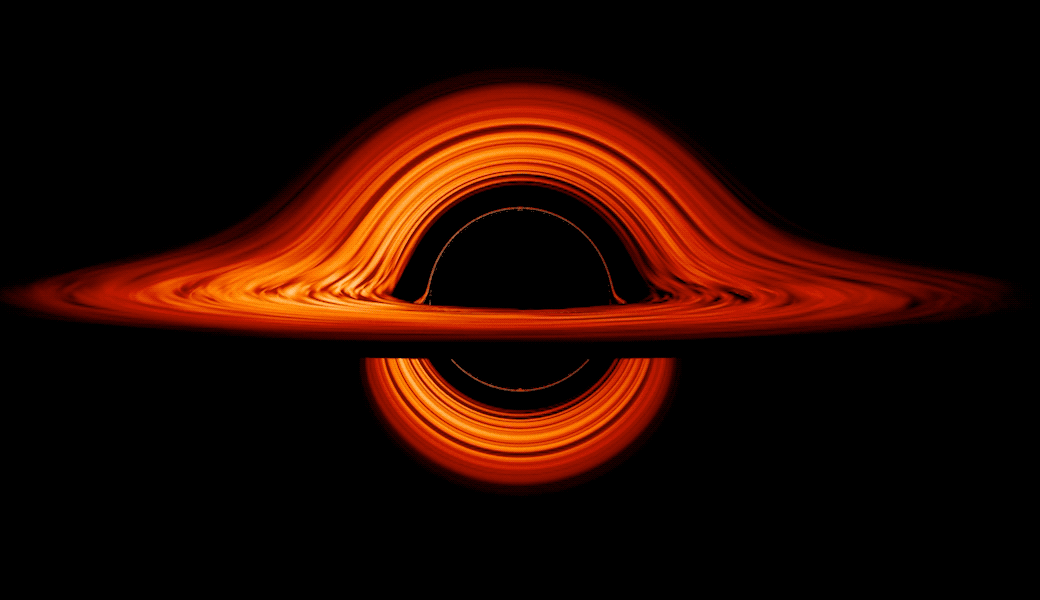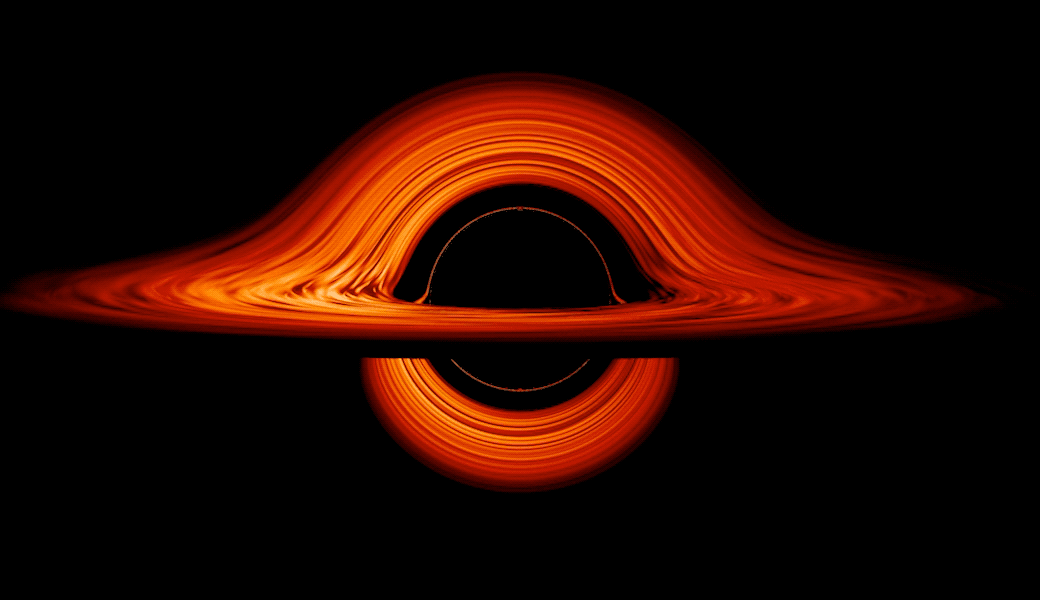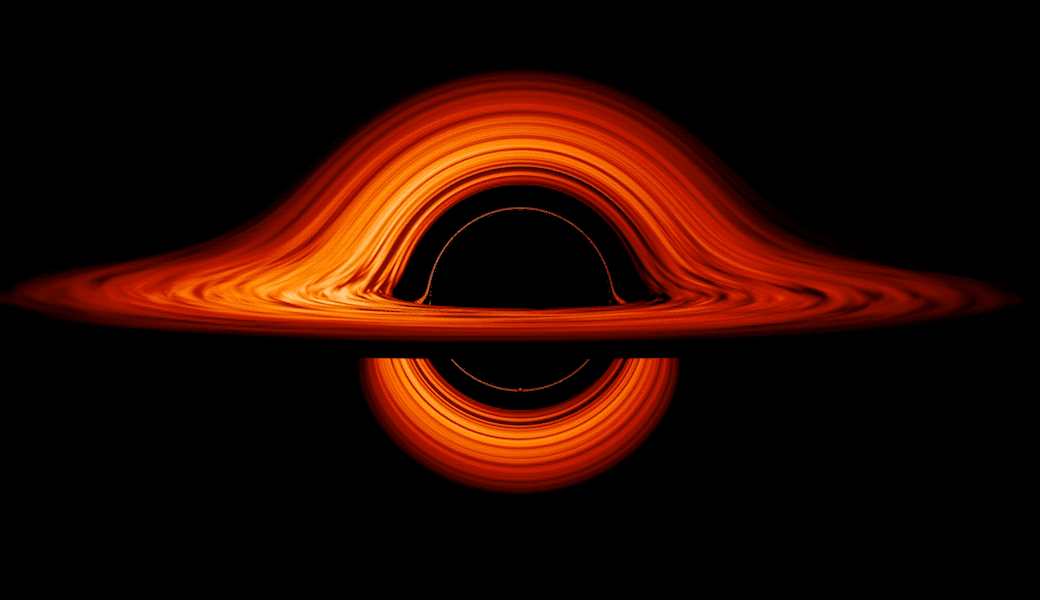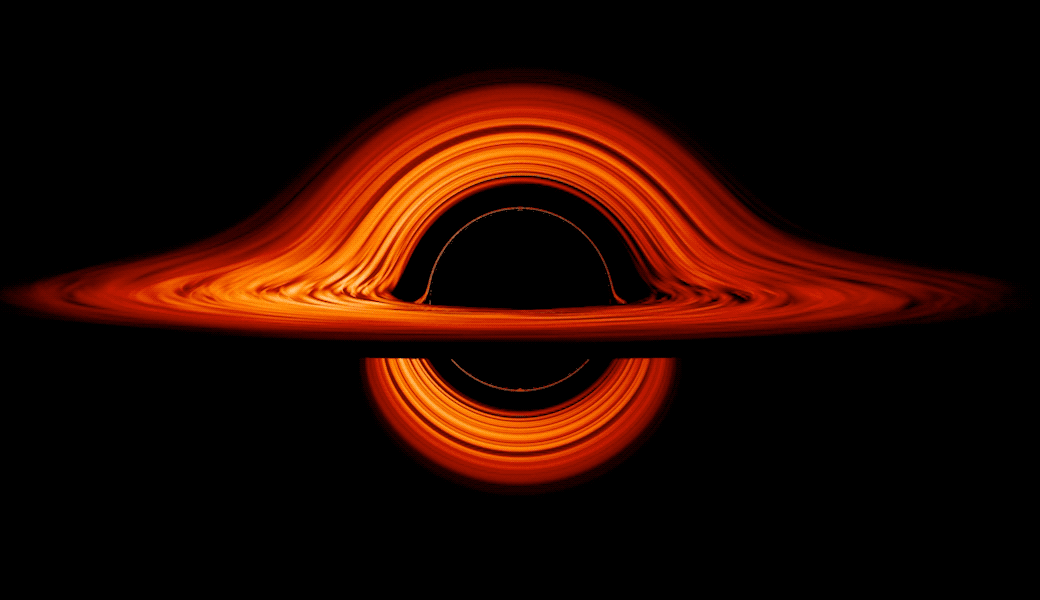
Трехмерная черная дыра
Модель падения в черную дыру
Определения
Черная дыра - область пространства, для которой вторая космическая скорость больше скорости света (v2k>c)
Горизонт событий - область пространства вокруг черной дыры, в которой вторая космическая скорость равна скорости света (v2k=c)
Масса черной дыры
\sqrt{\dfrac{2 G M}{r_g}}
Радиус горизонта событий (гравитационный радиус)
?
v_{2k}
=
\geqslant
c
Гравитационная постоянна
G = 6.67\cdot10^{-11} \, \dfrac{\text{Н}\cdot\text{м}^2}{\text{кг}^2}
Спасибо за понимание!
§ 8. Космические скорости
By Astro Group
