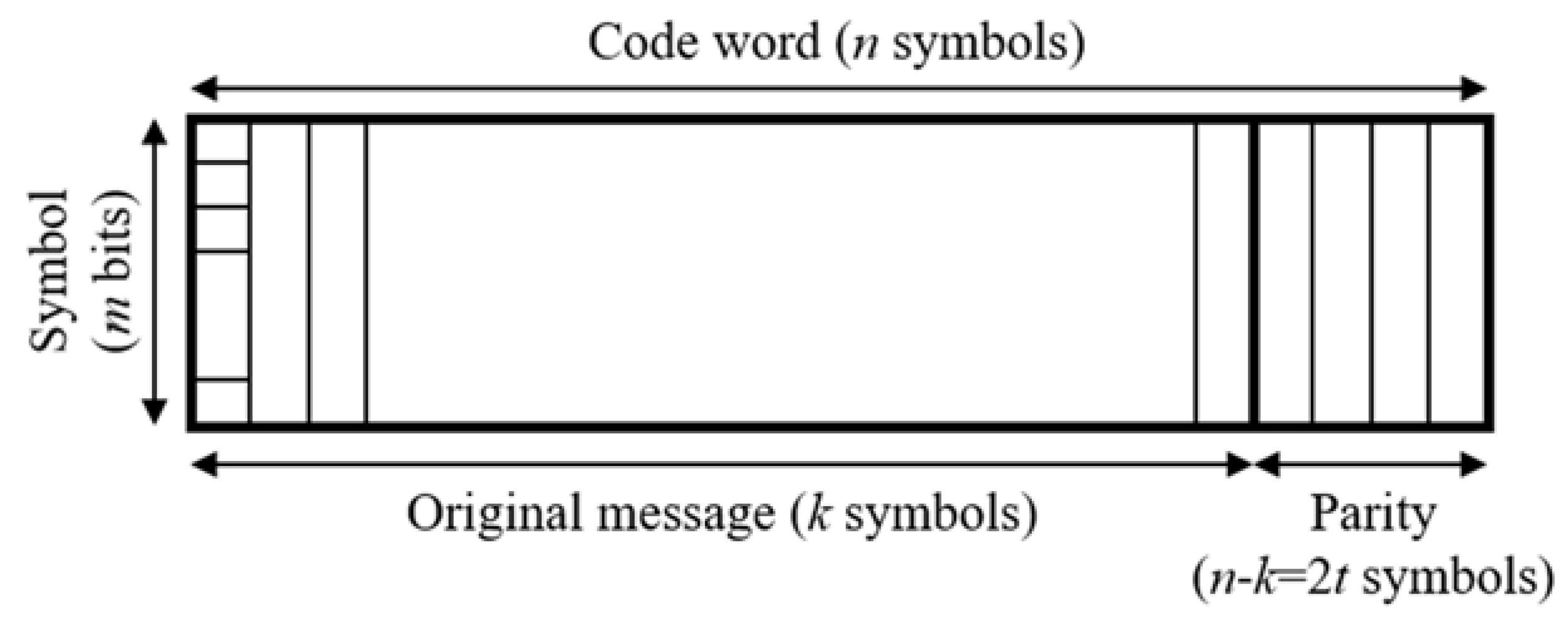
QR Code
Intro

import QRCode from 'qrcode';
import {
useRef,
useEffect,
} from 'react';
export default (url) => {
const canvas = useRef();
const urlRef = useRef();
useEffect(() => {
if (canvas.current) {
QRCode.toCanvas(canvas.current, url, (err) => {
if (err) {
debugQRCode(err);
}
});
}
}, [canvas, url]);
useEffect(() => {
urlRef.current = url;
}, [url]);
return canvas;
};
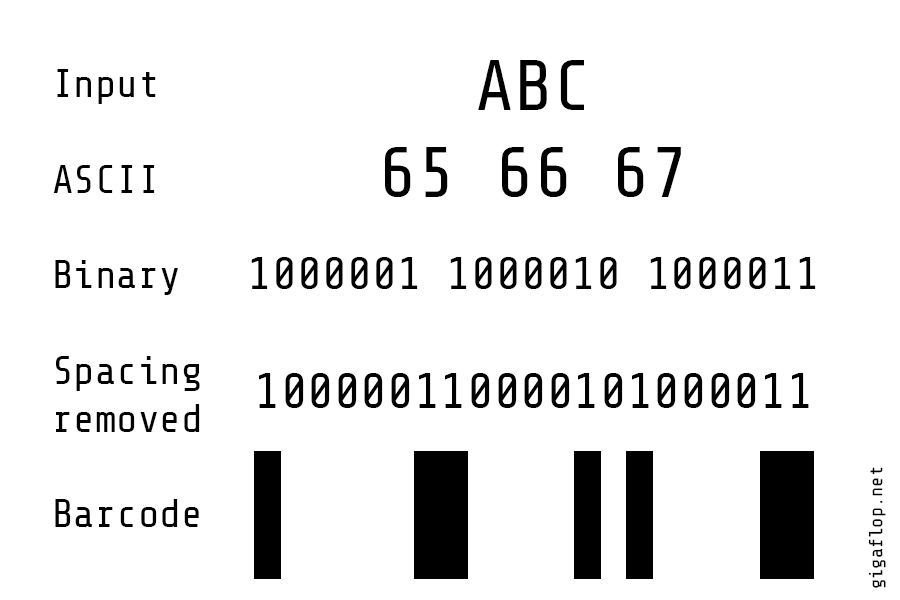
Before QR Code......
barcode

One-dimensional
two-dimensional
- find the smallest width
- translate width to binary
- left/right recognition
- parity
- translate binary to message (with table)
S.O.P.

- find the smallest width
- translate width to binary
- left/right recognition
- parity
- translate binary to message (with table)
S.O.P.

when we need carry more information.......
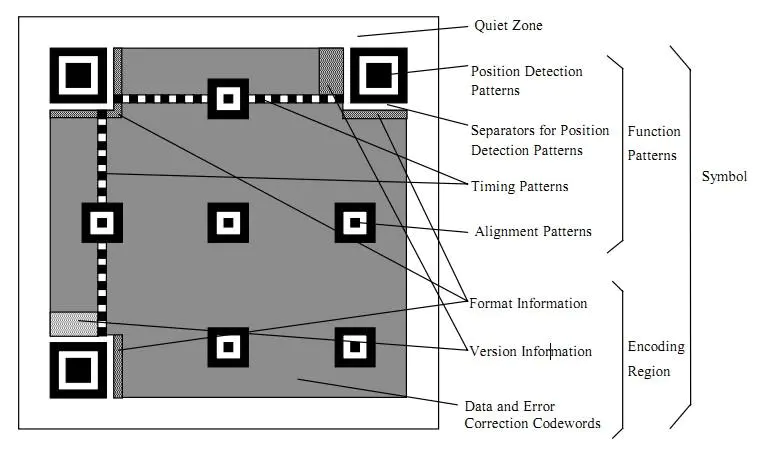
QR Code

Data Identification
Error correction

data
∝
size
Error correction
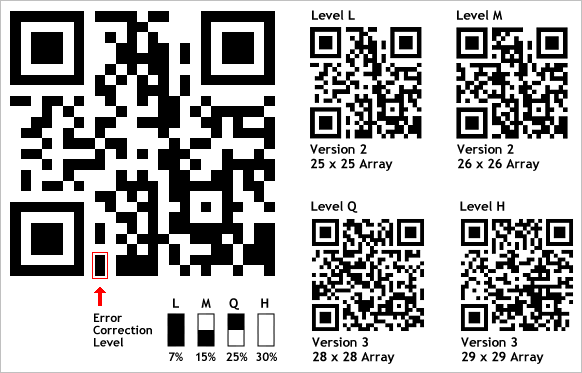

How ?
Error correction
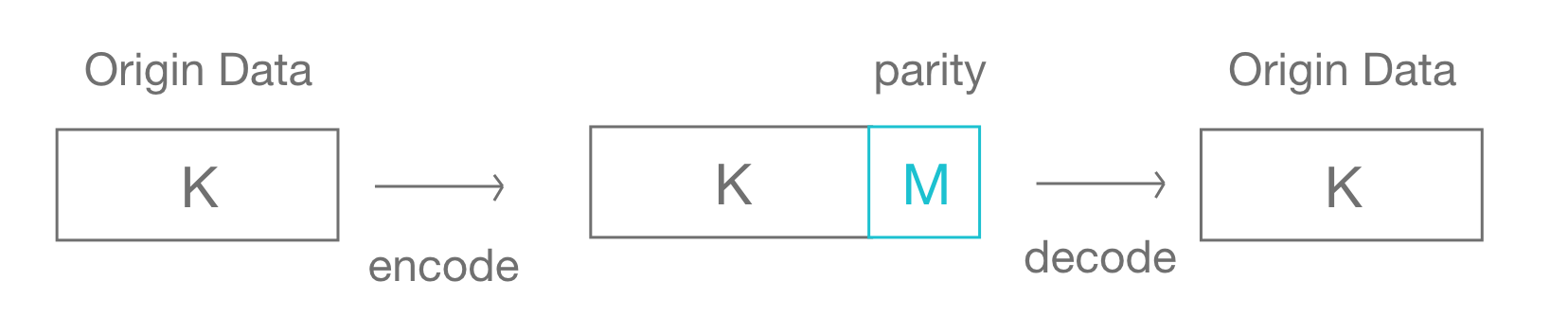
Even if part of the data is lost, it can still be restored to the original data
First, we need to know two things
position
offset
position: e1, e2
offset: y1, y2
e1=3
e2=1
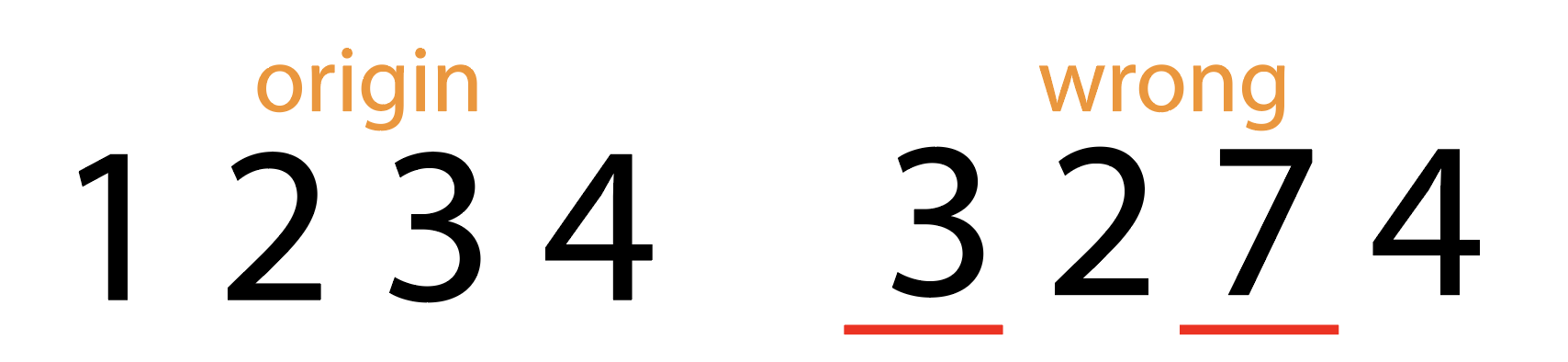
y1=2
y2=4




addition/subtraction ?
K - M = 0
division/remainder ?
K % M = 0
position
offset
condition ?


Galois Field

Galois Field
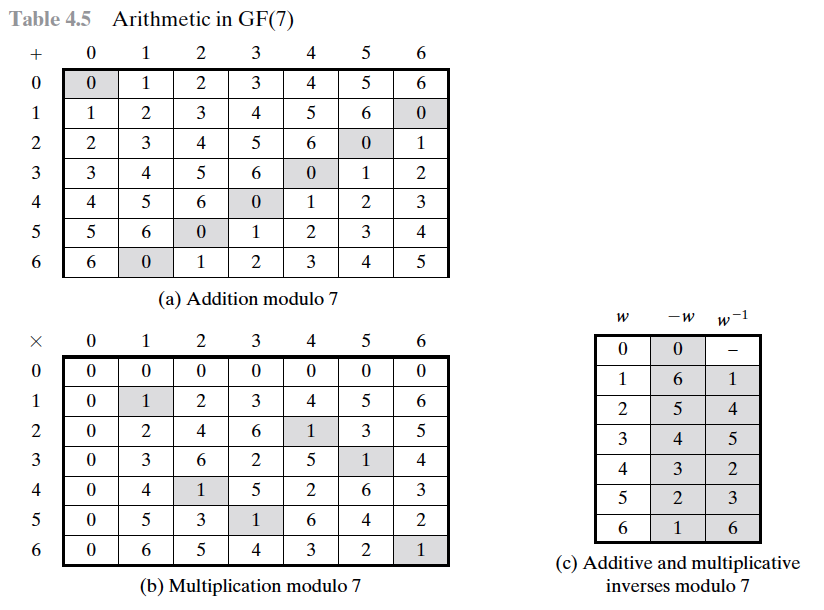
5+6 = 11(mod7) = 4
GF(m)
5*6 = 30(mod7) = 2
m should be prime number
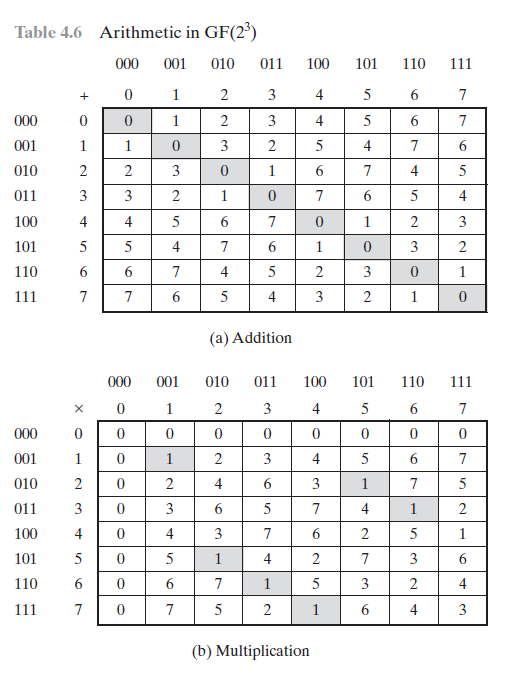
GF(8)?
GF(2^3)
represent the elements with polynomials

GF(8)?
GF(2^3)
prime number?
1011
represent the elements with polynomials(in binary)
X^3 + x + 1
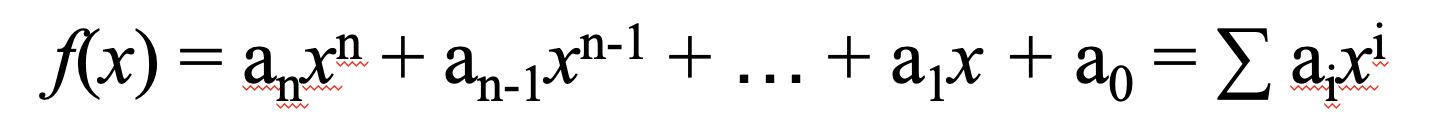
7 = 111(binary)
= x^2 + x + 1

addition: xor
multiply:
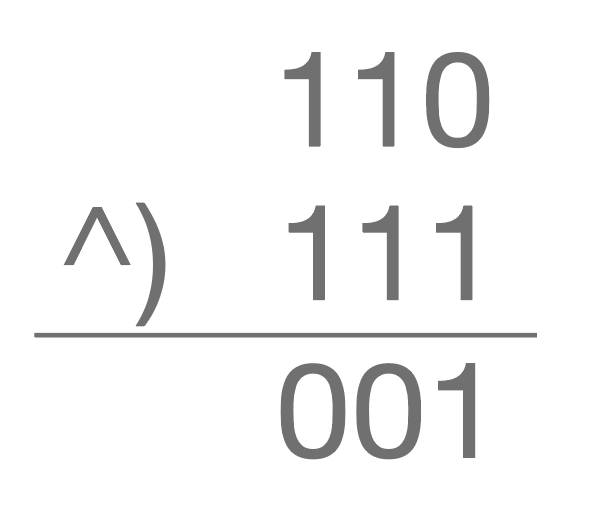

addition: xor
multiply:
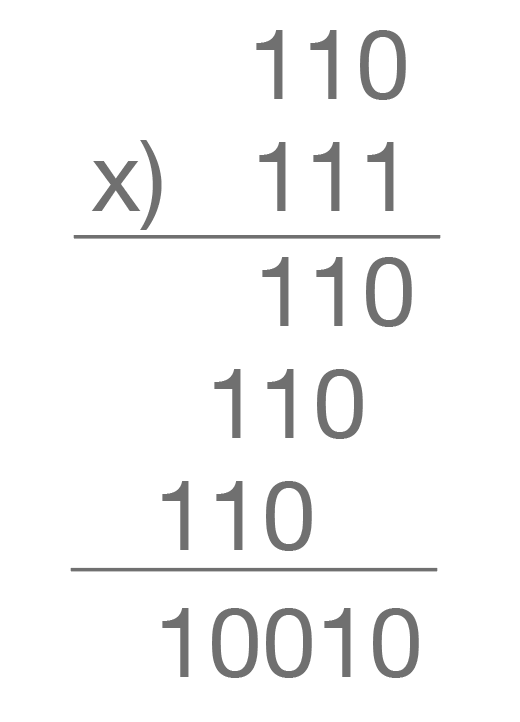
1. xor
2. divide by prime number
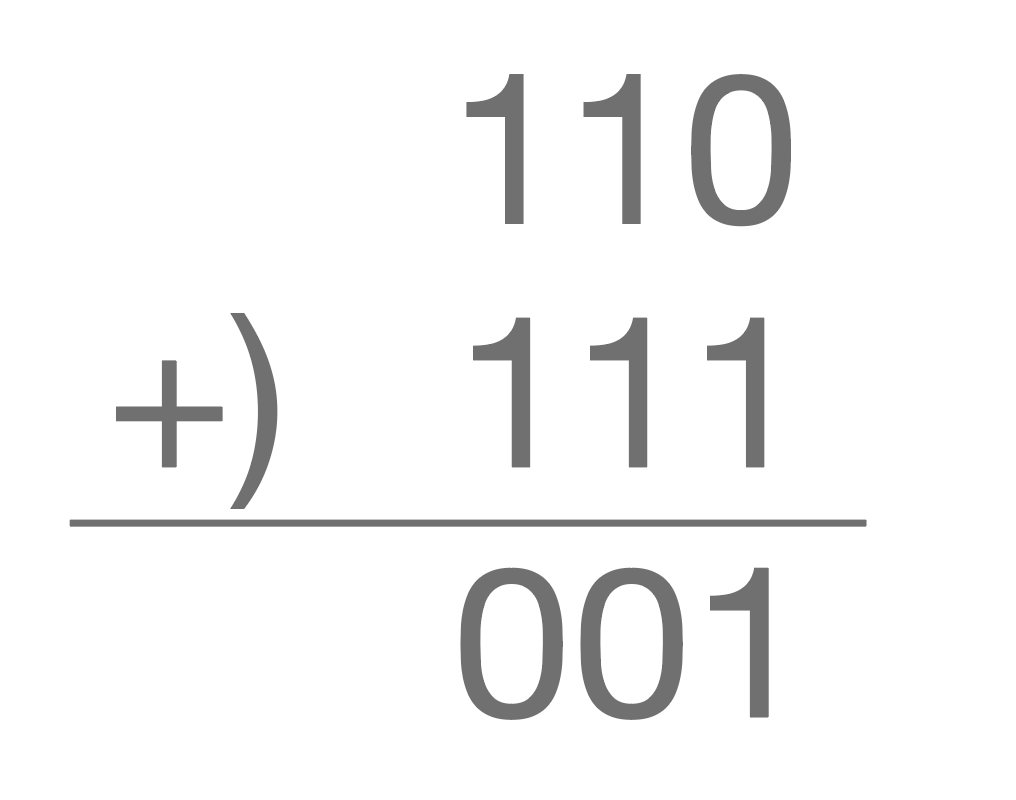
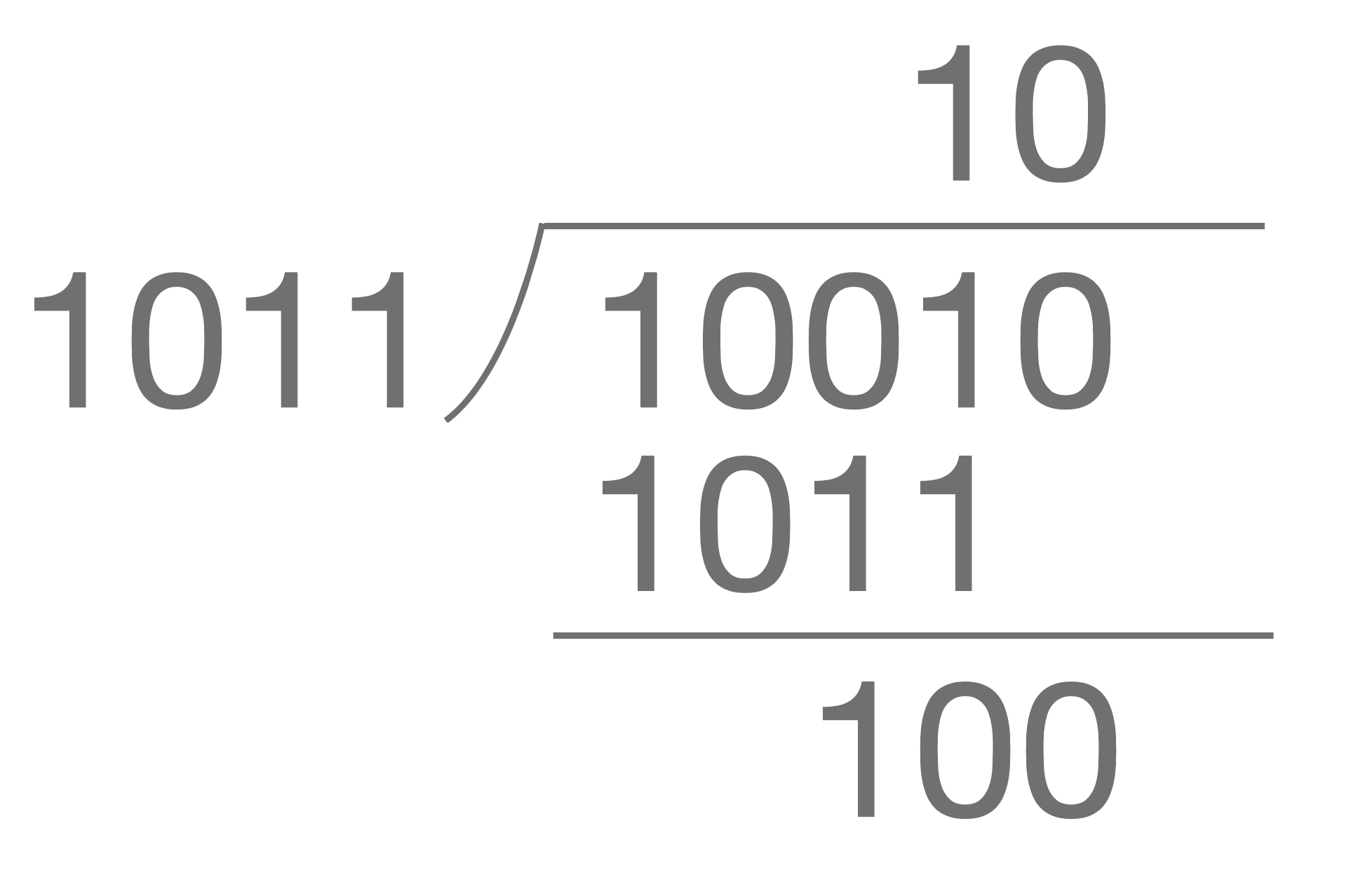
Reed-Solomon
Reed-Solomon codes are a signal processing technique to correct errors.Based on Galois field.
They are nowadays ubiquitous, such as in communications (mobile phone, internet), data storage and archival (hard drives, optical discs CD/DVD/BluRay, archival tapes), warehouse management (barcodes) and advertisement (QR codes)
Example 🌰
1234abcd
1234
message
message
parity
Represent it with Polynomial
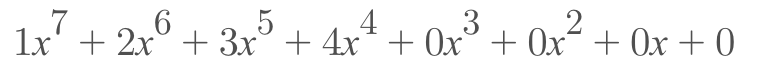
message
+
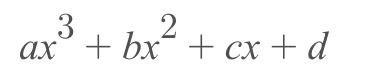
parity
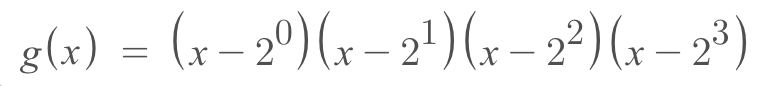
m(x)
p(x)
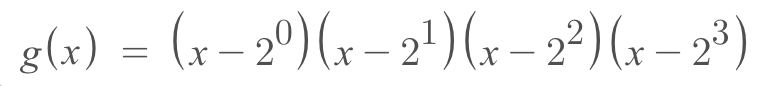
Base on Galois Field
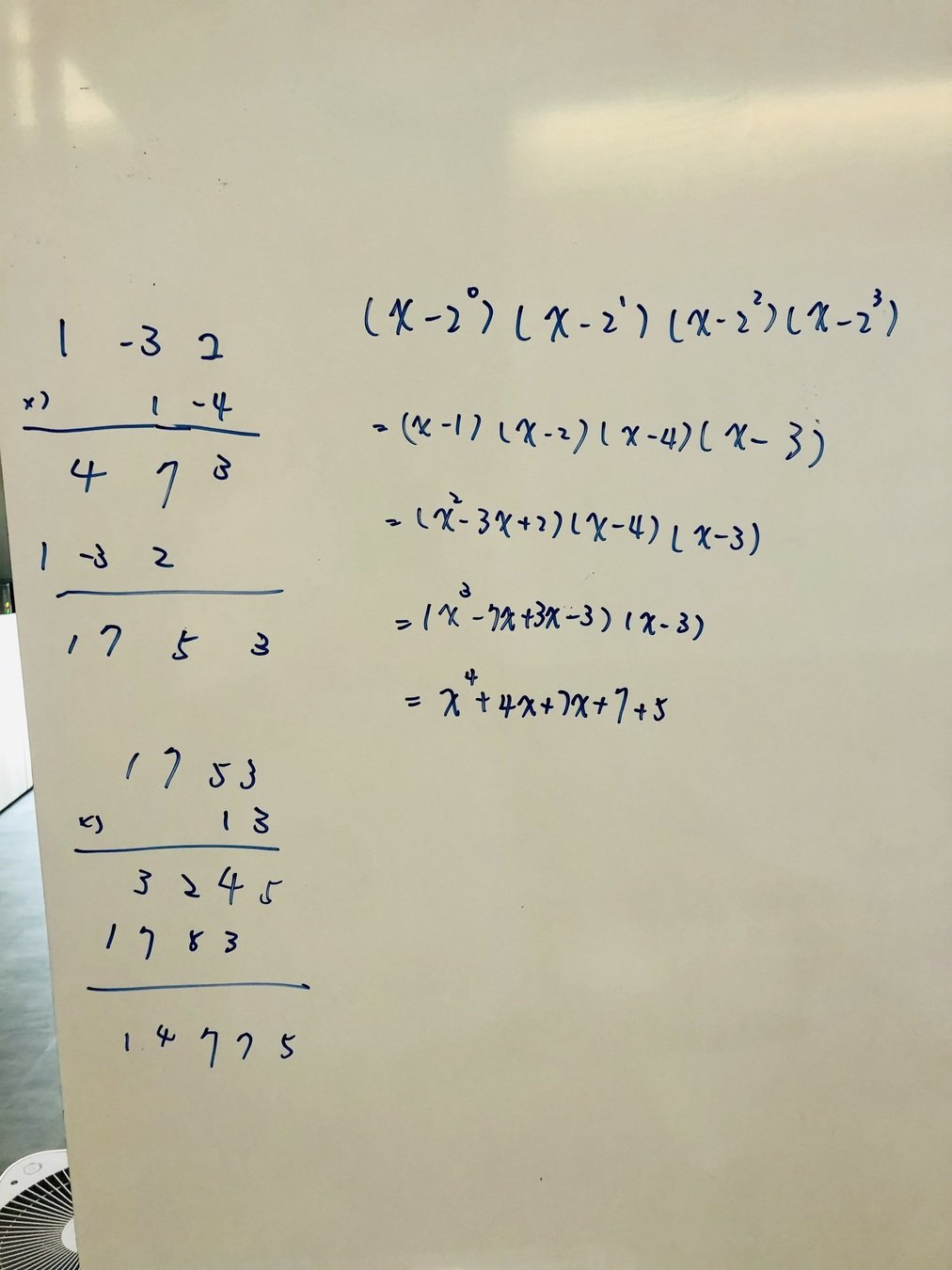
m(x)
g(x)
p(x)
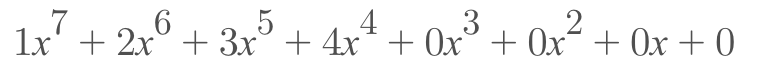
message
+
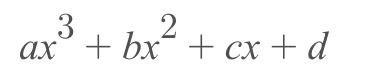
parity
m(x)
p(x)
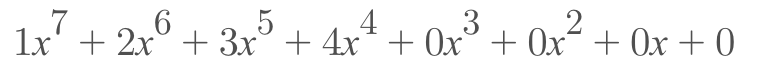
message
+
parity
m(x)
p(x)
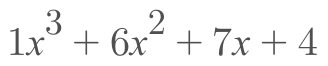
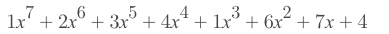
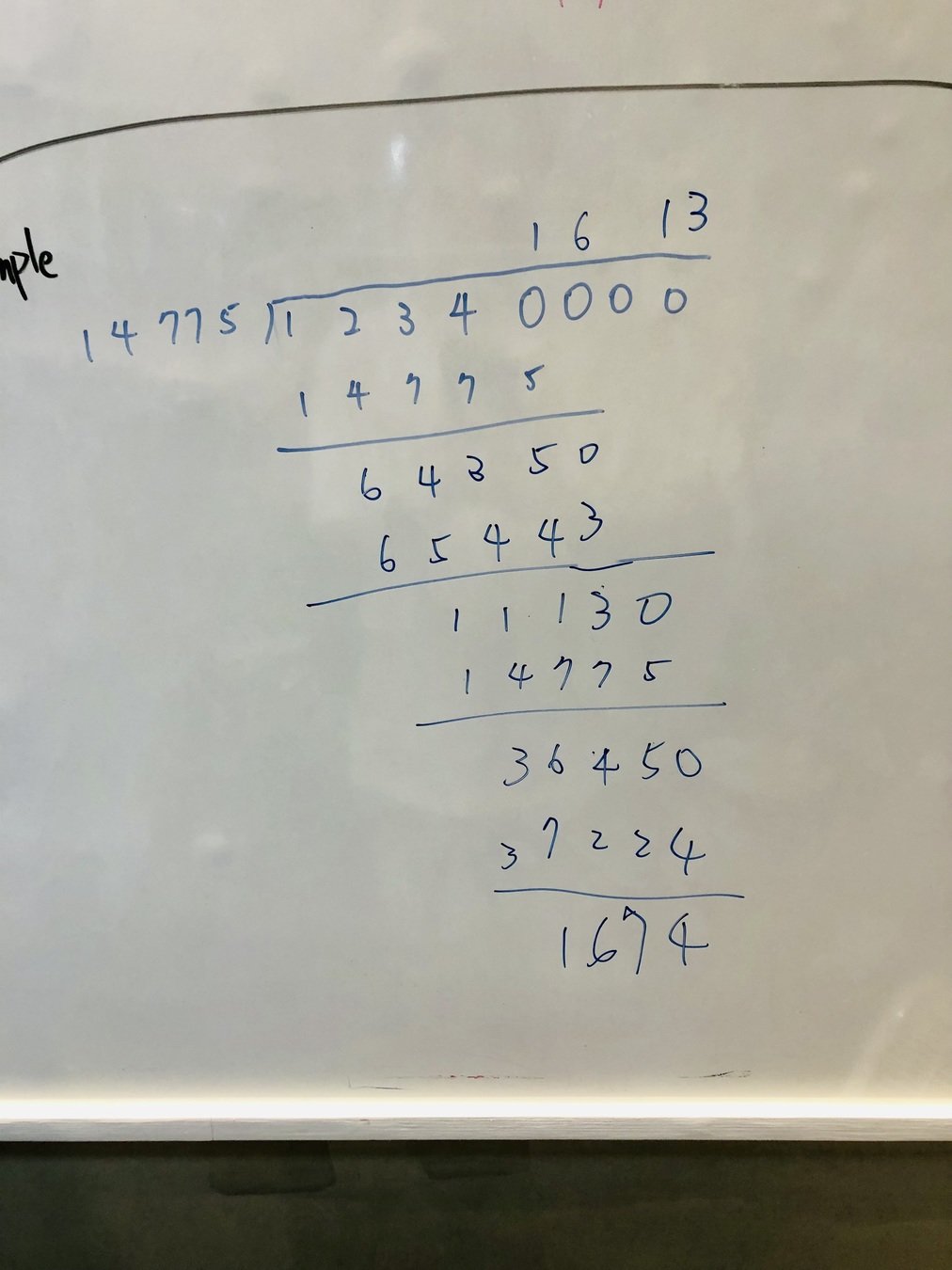
new Message M(x)
12341674

62241674
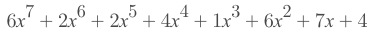
Wrong Message

should be 0
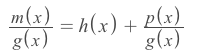
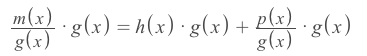
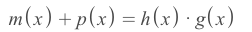
m(x): message
g(x): generate
p(x): parity
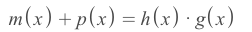
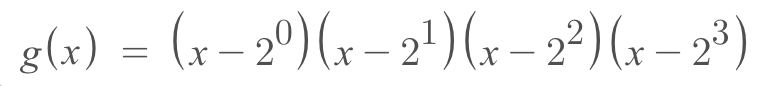
If x = 2^0, 2^1, 2^2, 2^3
g(x) = 0, M(x) = 0
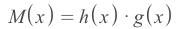
Verify
62241674
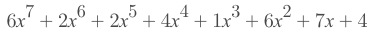
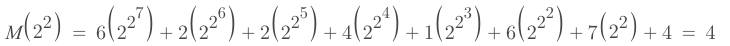
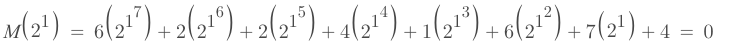
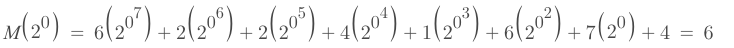
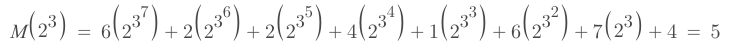
Substitute x into M(x)
Wrong Message

position: e1, e2
offset: y1, y2
e1= 5, e2 = 7
y1=1, y2 = 7
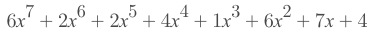

position: e1, e2
offset: y1, y2
e1= 5, e2 = 7
y1=1, y2 = 7
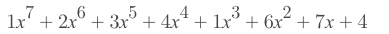


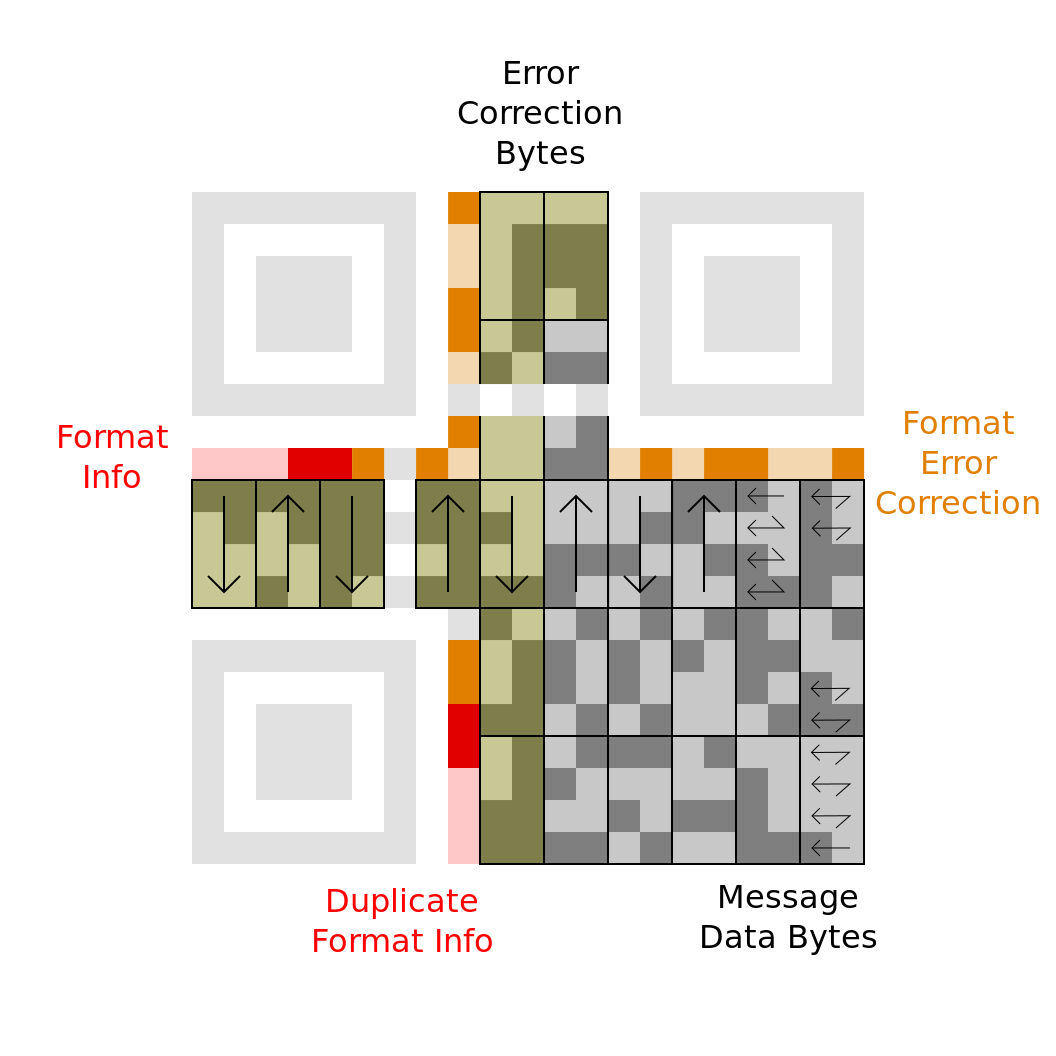

A masking process is used to avoid features in the symbol that might confuse a scanner, such as misleading shapes that look like the locator patterns and large blank areas.
QA
QA
QR Code
By Jay Chou
QR Code
- 600



