Recommender Systems
Avraam Mavridis
@avraamakis
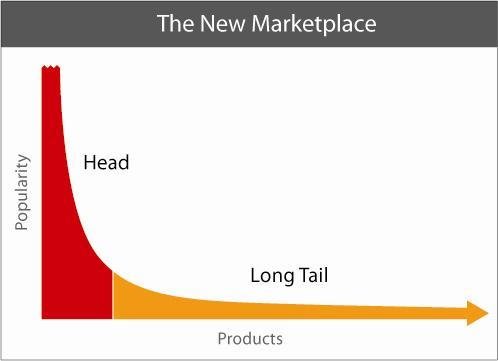
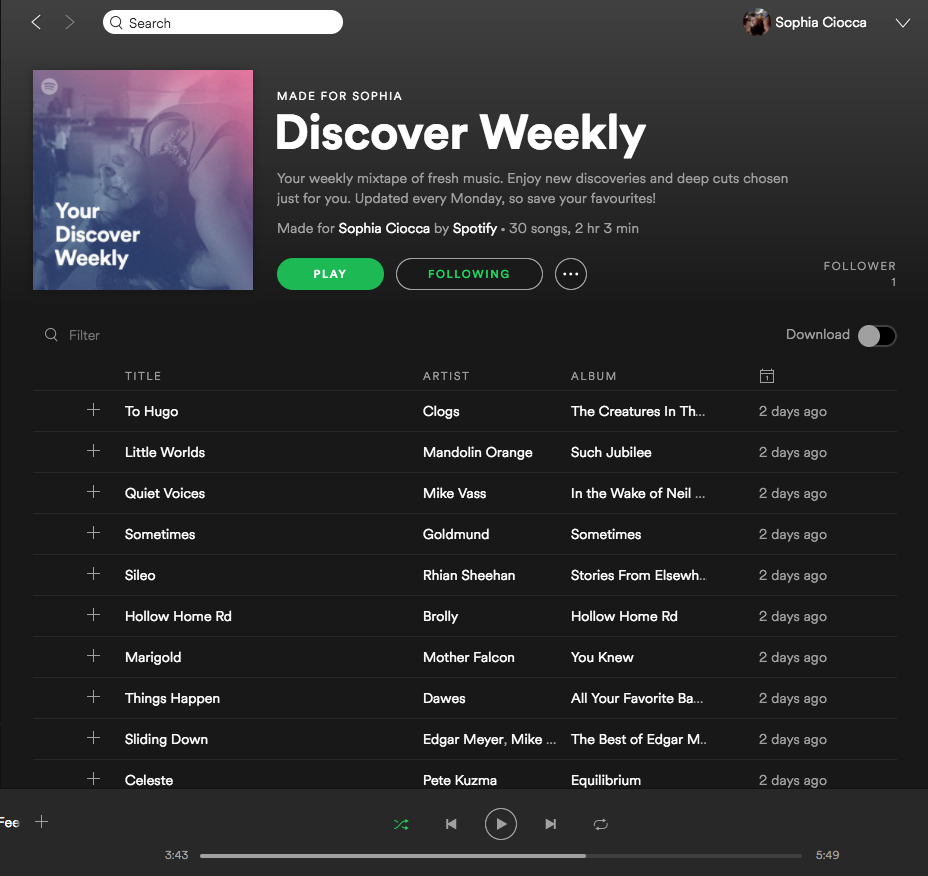

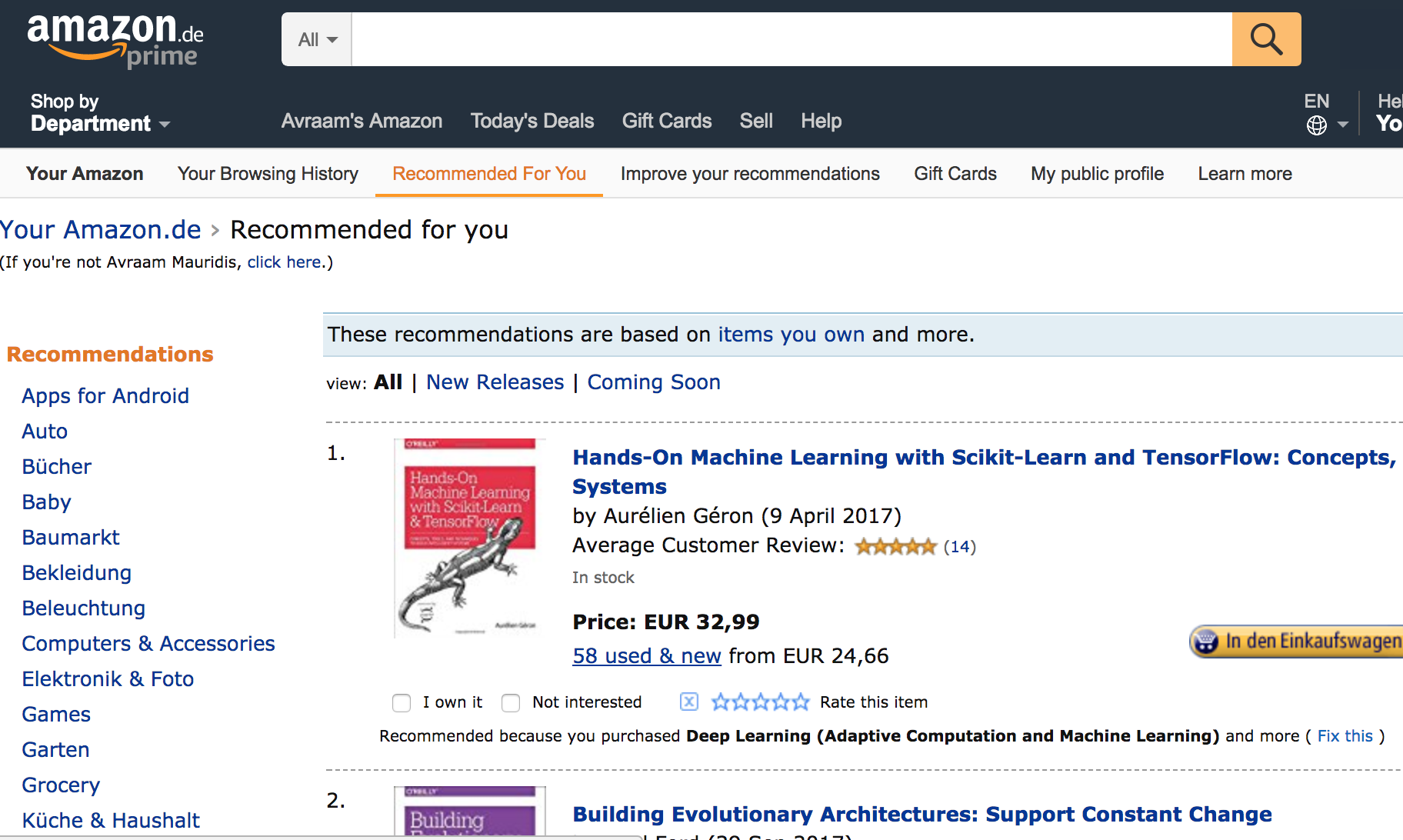
Collaborative Filtering
- Use historical data on purchasing behavior
- Find similar users
- Predict users' interest based on a similarity metric
Collaborative Filtering
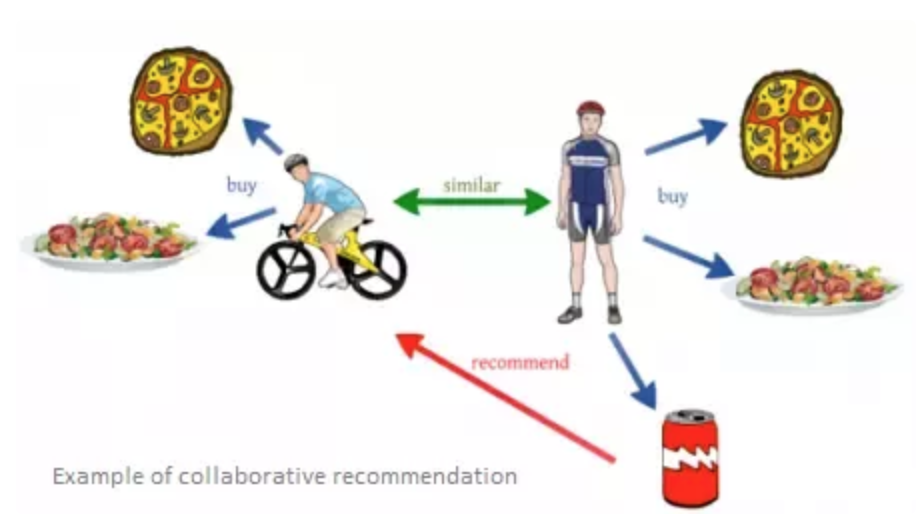
Collaborative Filtering
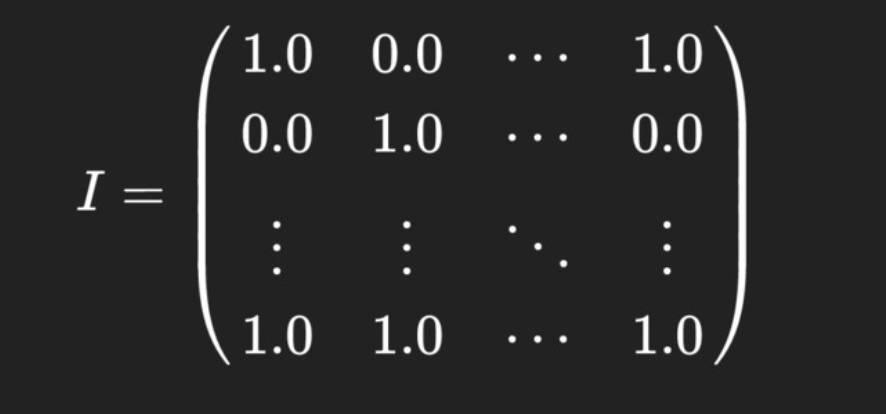
User Interaction Matrix
Collaborative Filtering
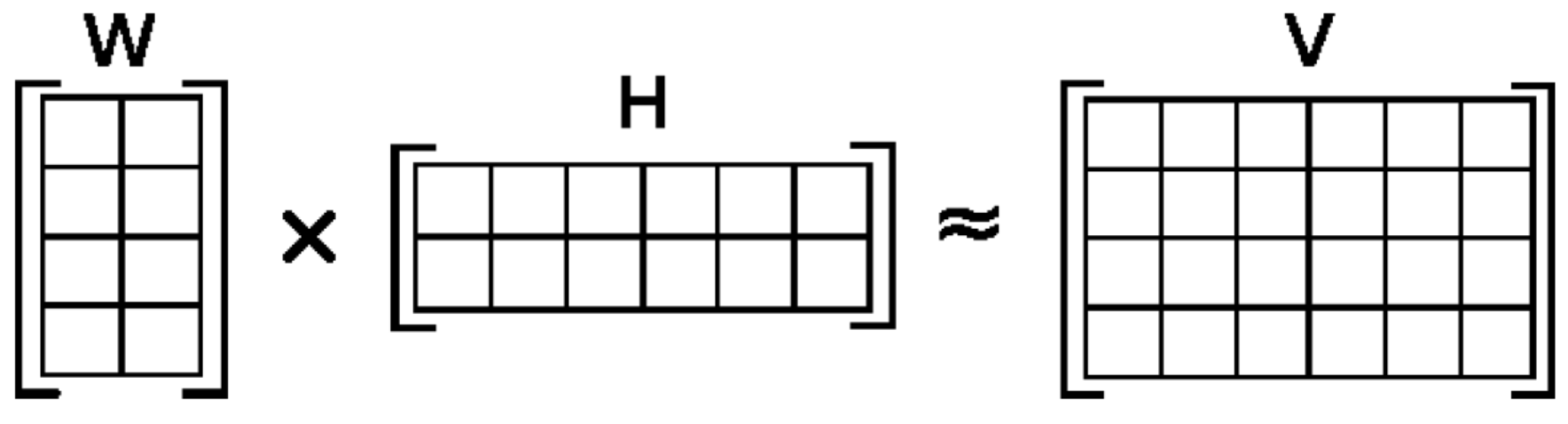
Let matrix V be the product of the matrices W and H,
V = WH.
Matrix multiplication can be implemented as computing the column vectors of V as linear combinations of the column vectors in W using coefficients supplied by columns of H.
Utility Matrix

The goal of the recommendation system is to predict the blanks in the utility matrix
How we usually create a Utility Matrix
- We can ask users to rate items (but users usually are unwilling to provide responses)
- We can make inferences from users' behavior
Similarity/Distance Metrics
| Inception | Interstellar | Memento | Insomnia | Matrix | Quay | Prestige | |
|---|---|---|---|---|---|---|---|
| Bob | 4 | 5 | 1 | ||||
| Alice | 5 | 5 | 4 | ||||
| Dinos | 2 | 4 | 5 | ||||
| Nick | 3 | 3 |
Similarity/Distance Metrics
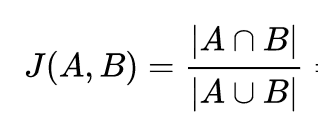
Jaccard Index
Similarity/Distance Metrics
Jaccard Index
| Inception | Interstellar | Memento | Insomnia | Matrix | Quay | Prestige | |
|---|---|---|---|---|---|---|---|
| Bob | 4 | 5 | 1 | ||||
| Alice | 5 | 5 | 4 | ||||
| Dinos | 2 | 4 | 5 | ||||
| Nick | 3 | 3 |
Bob and Alice have intersection size 1 and union size 5, their Jaccard distance is 1/5 = 0.2.
In comparison, Bob and Dinos have intersection size 2 and union size 4, their Jaccard distance is 2/4 = 0.5
Thus Bob appears close to Dinos than Alice...
Similarity/Distance Metrics
Euclidean / Manhatan / Minkowski

Similarity/Distance Metrics
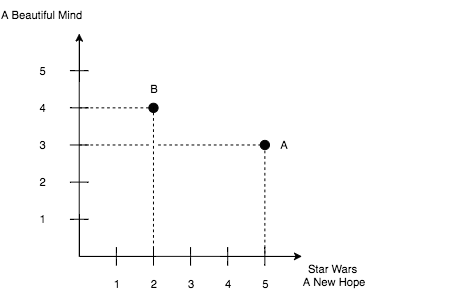
Euclidean distance
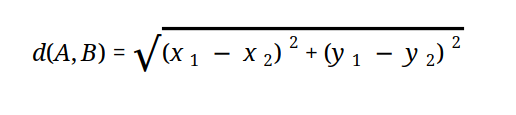
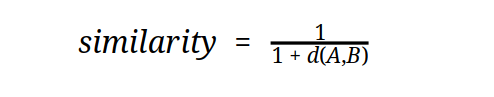
Similarity/Distance Metrics
Euclidean distance
def euclidean_distance(moviesUser1, moviesUser2, threshold = 3):
movies1 = map(lambda x: x['movieId'], moviesUser1)
movies2 = map(lambda x: x['movieId'], moviesUser2)
intersection = [val for val in movies1 if val in movies2]
sum = 0
for key in intersection:
match1 = filter(lambda x: x['movieId'] == key, moviesUser1)
match2 = filter(lambda x: x['movieId'] == key, moviesUser2)
sum += math.sqrt(pow(float(match1[0]['rating']) - float(match2[0]['rating']), 2))
return 1 / (1+sum)Similarity/Distance Metrics
Euclidean distance
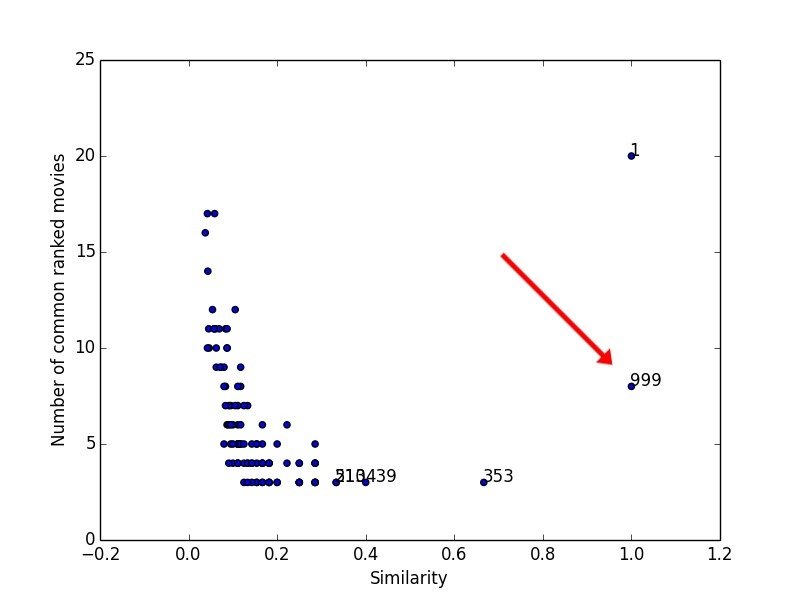
999,1953,4.0
999,2105,4.0
999,2150,3.0
999,2193,2.0
999,2294,2.0
999,2455,2.5
999,3671,3.0
999,2968,1.0Similarity/Distance Metrics
Euclidean distance
999,1953,4.0
999,2105,4.0
999,2150,3.0
999,2193,2.0
999,2294,2.0
999,2455,2.5
999,3671,3.0
999,2968,3.0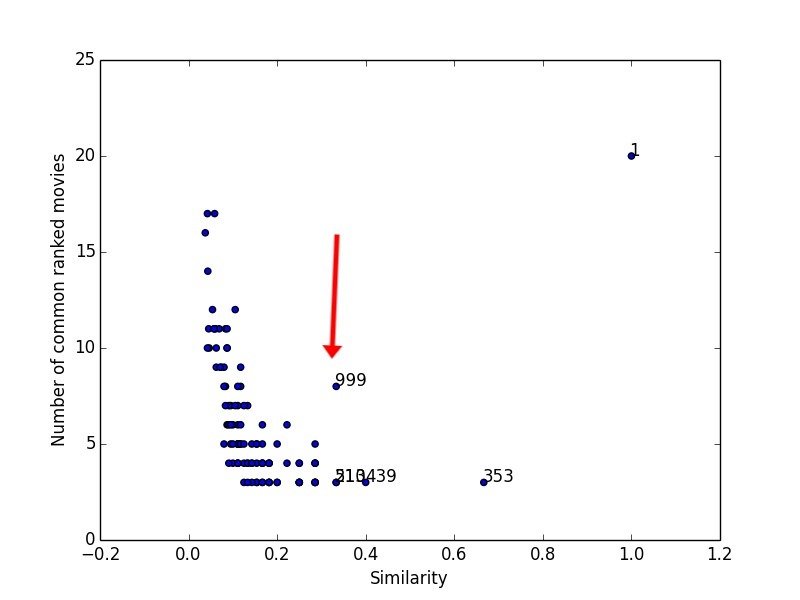
Similarity/Distance Metrics
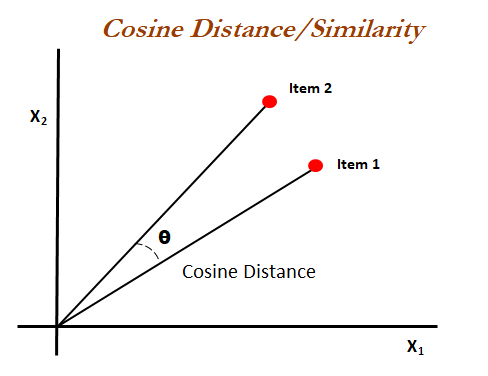
Cosine Distance
Similarity/Distance Metrics
Cosine Similarity
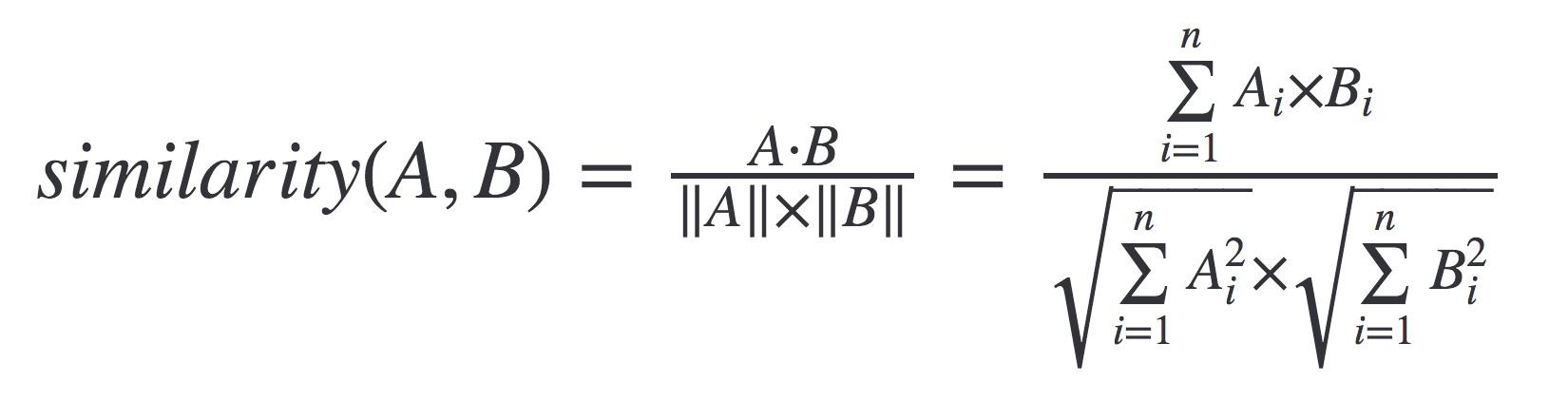
Cosine similarity is the cosine of the angle between two n-dimensional vectors in an n-dimensional space. It is the dot product of the two vectors divided by the product of the two vectors' lengths (or magnitudes)
Similarity/Distance Metrics
Cosine Similarity
| Inception | Interstellar | Memento | Insomnia | Matrix | Quay | Prestige | |
|---|---|---|---|---|---|---|---|
| Bob | 4 | 5 | 1 | ||||
| Alice | 5 | 5 | 4 | ||||
| Dinos | 2 | 4 | 5 | ||||
| Nick | 3 | 3 |
Bob Vs Dinos
= 0.322
Bob vs Alice
= 0.38
Similarity/Distance Metrics
Cosine Similarity
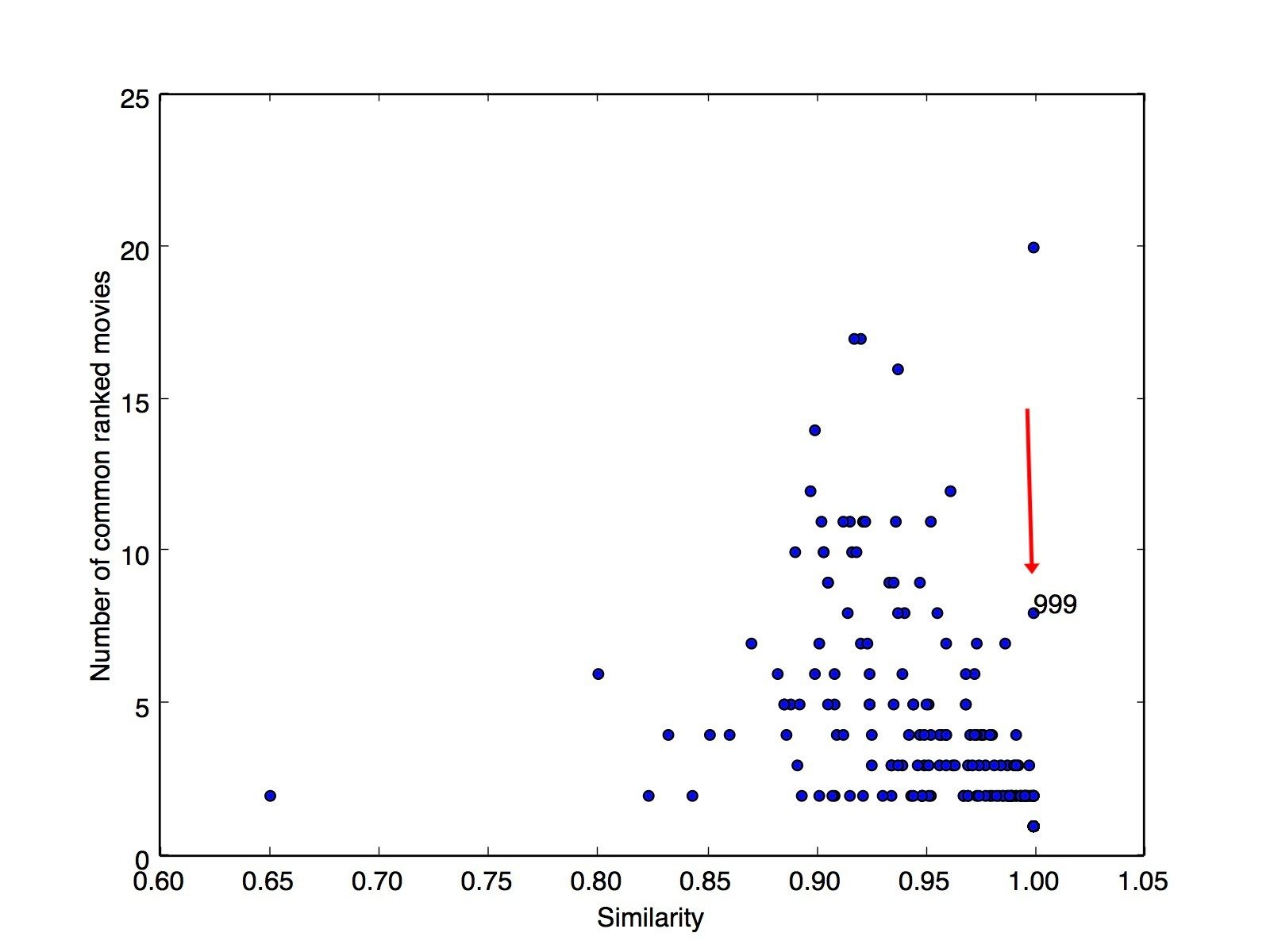
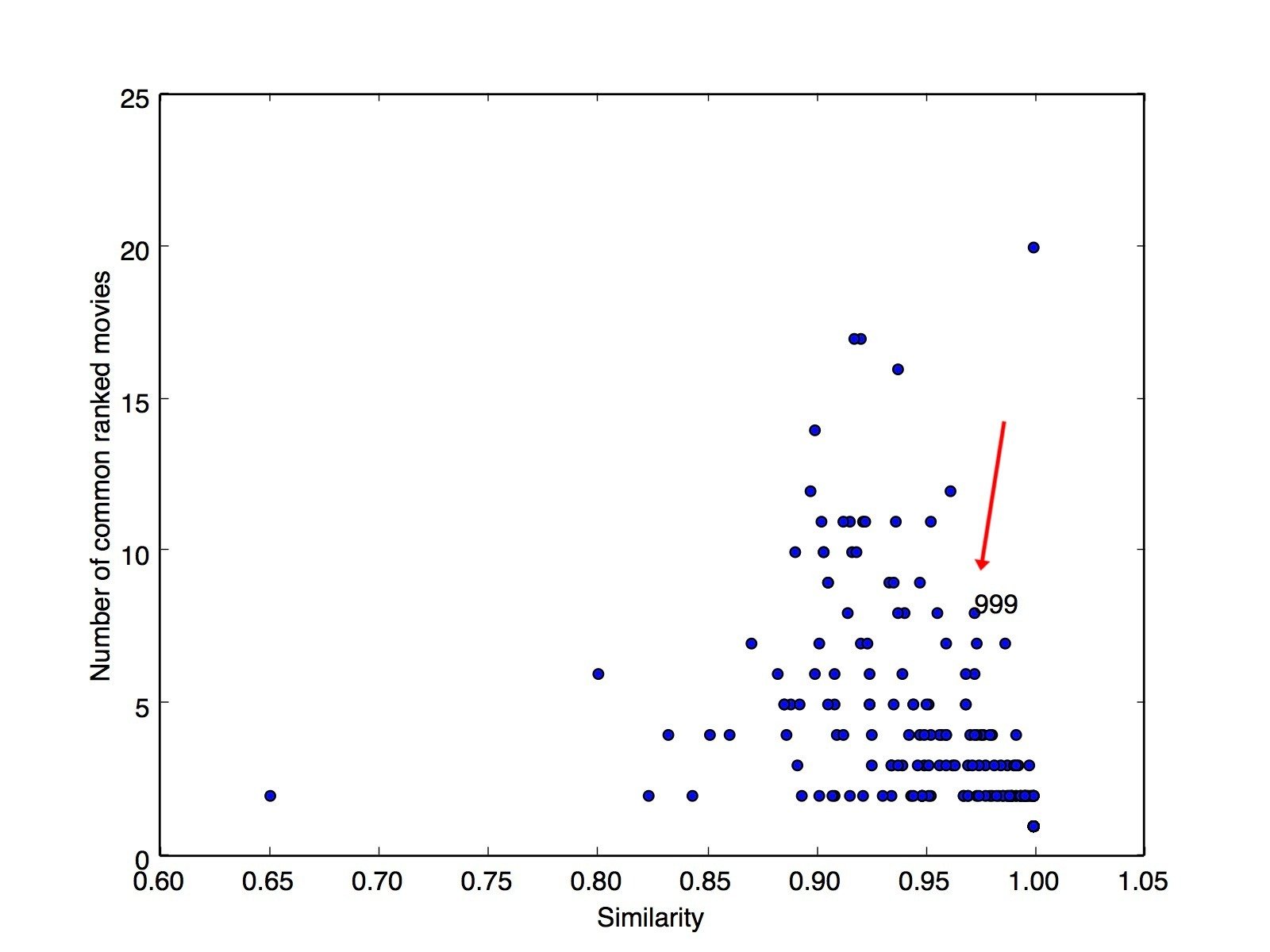
Similarity/Distance Metrics
Pearson correlation coefficient
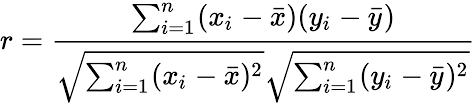
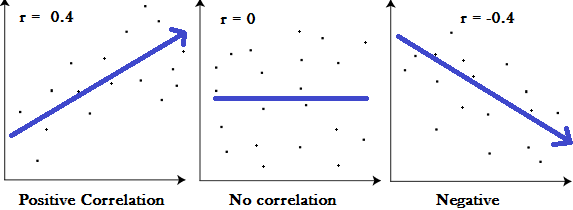
The Pearson correlation coefficient is a measure of the linear correlation between two variables. It gives a number between -1 and 1, where -1 is a total negative linear correlation, a value of 0 means no linear correlation and a value of 1 is a total positive linear correlation.
Usually that is enough to make recommendations
- Find similar users based on a distance metric
- Recommend items similar users have bought
- Almost domain-agnostic
- Easy to understand and implement
BUT...
- What if you have a millions of products?
- What would you recommend to new users?
- What if you have short-lived items (e.g. news articles)?
- What if you don't have enough data about the users (cold start)?
NO BETTER THAN RANDOM
Content Based Models
- Use metadata of the items
- Use a classifier
- Recommend item to the user based on the class of items he is interested
KNN (k-nearest neighbors algorithm)
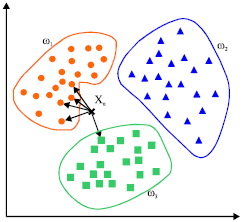
TFIDF (term frequency–inverse document frequency)

PROBLEMS
- Data and metadata about items required, not always available
- It doesnt share information across users
NEURAL NETWORK MODEL
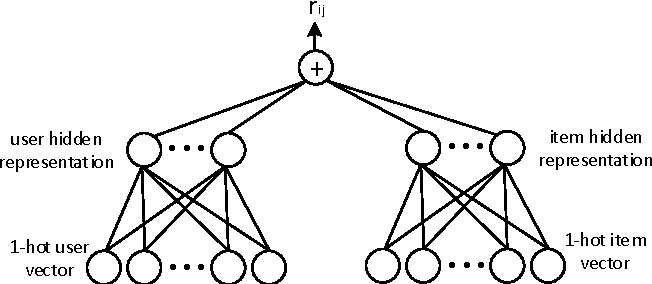
NEURAL NETWORK MODEL
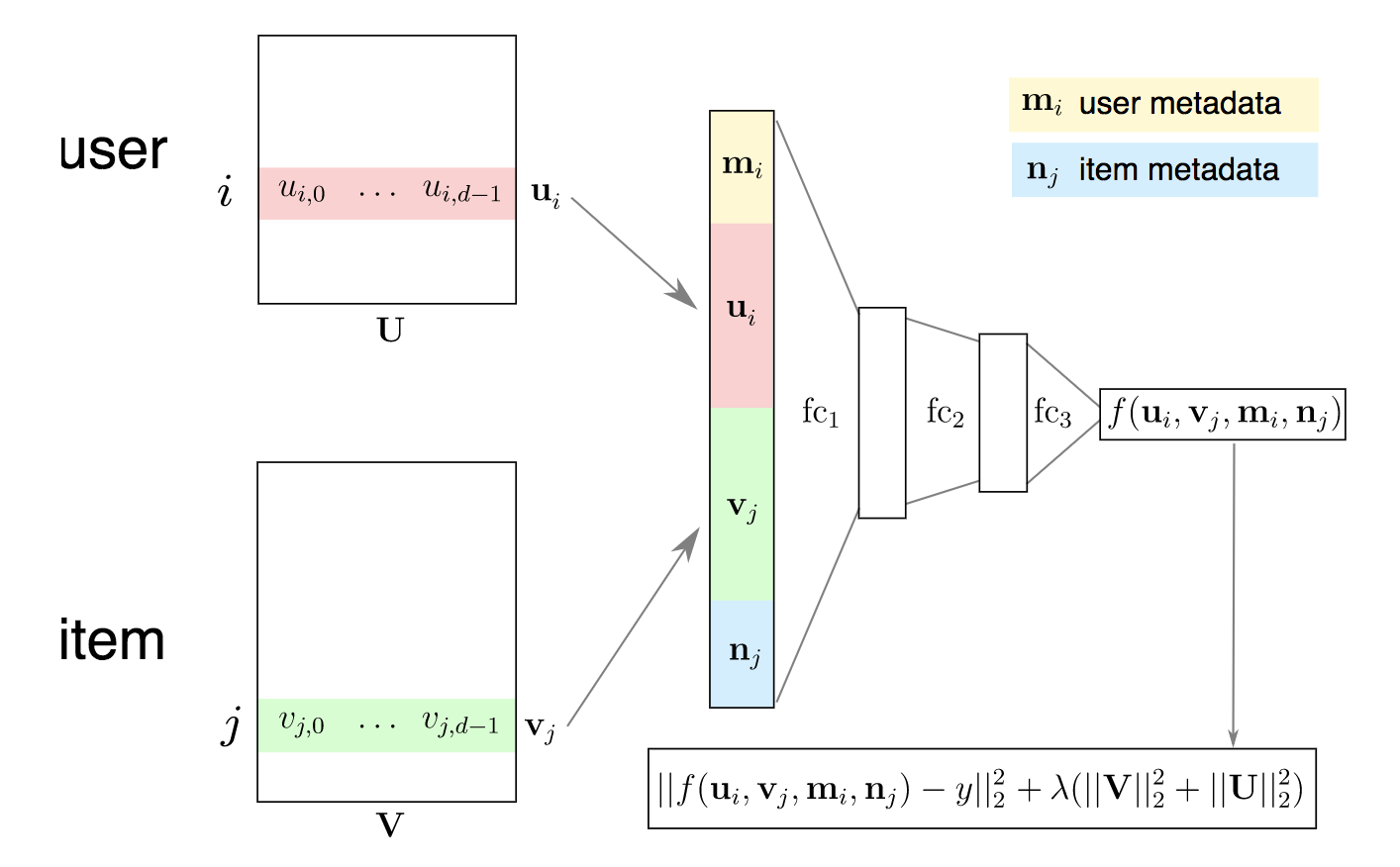
SUMMARY
- Understand your domain
- Pay attention to metadata
- Mix various models
- Evaluate the results (tricky)
Ethical Considerations
- Amplification of the filter bubble and opinion polarization
- Lack of transparency
Thank you
Recommender Systems
By Avraam Mavridis
Recommender Systems
- 1,539



