Category Theory for Programmers:
Categories Great and Small
Smallest Category => No Objects
Is this Void in the Category of All Categories?
Generate Categories from Graphs
=> Free Categories
1. Add Identity Arrows
2. Compose Morphisms
Generate a free category from:
A graph with one node and no edges
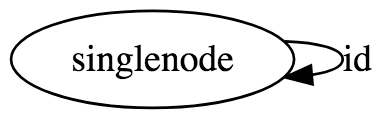
Generate a free category from:
A graph with one node and one (directed) edge (hint: this edge can be composed with itself)
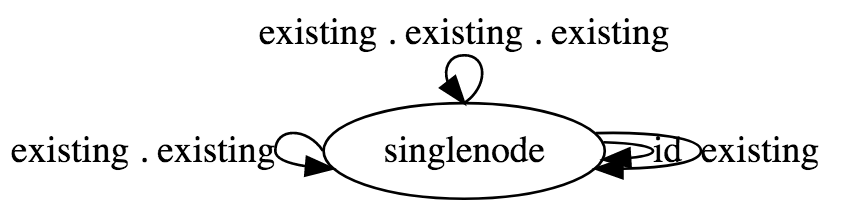
Generate a free category from:
A graph with two nodes and a single arrow between them

Generate a free category from:
A graph with a single node and 26 arrows marked with the letters of the alphabet: a, b, c ... z.
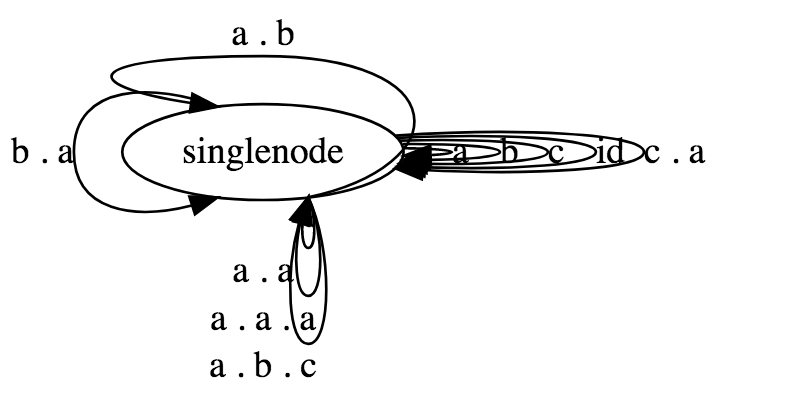
Orders
minimum order to be a category?
Partial order:
Preorder:
every two objects need to relate to each other
Example: reachability in a directed graph with cycles
Example: numbers <=
a <= b & b <= c => a <= cTotal order:
a <= b & b <= a => a == bWhat kind of order is this?
A set of sets with the inclusion relation: A is included in B if every element of A is also an element of B.
=> Partial order
Not all sets are related. For example: {1} and {2,3}
A \subseteq A
A \subseteq B\ \&\ B \subseteq C \Rightarrow A \subseteq C
A \subseteq B\ \&\ B \subseteq A \Rightarrow A = B
What kind of order is this?
C++ types with the following subtyping relation: T1 is a subtype of T2 if a pointer to T1 can be passed to a function that expects a pointer to T2 without triggering a compilation error.
=> Partial order
Not all types are subtypes.
A \subseteq A
A \subseteq B\ \&\ B \subseteq C \Rightarrow A \subseteq C
A \subseteq B\ \&\ B \subseteq A \Rightarrow A = B ???
Monoids
set with a binary operation
associative
neutral element
(a - b) - c = a - (b - c)0 - a = a
a - 0 = aNot a Monoid
not associative
no neutral element
(a - b) - c = a - (b - c)
(5 - 4) - 1 = 5 - (4 - 1)
0 = 20 - a = -a
a - 0 = aConsidering that Bool is a set of two values True and False, show that it forms two (set-theoretical) monoids with respect to, respectively, operator & (AND) and | (OR).
a & (b & c) = (a & b) & c
a | (b | c) = (a | b) | c
a & true = a
true & a = a
a | false = a
false | a = aMonoids as a Category
Monoid => Mono => Single object Category
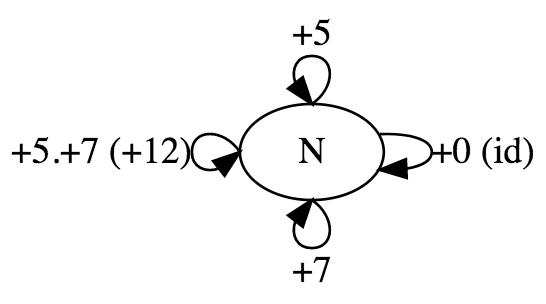
mappend maps from integers to adders
mappend : Int -> (Int -> Int)Homset
Morphisms => Set (HomSet)
only for locally small categories
Represent the Bool monoid with the AND operator as a category: List the morphisms and their rules of composition.
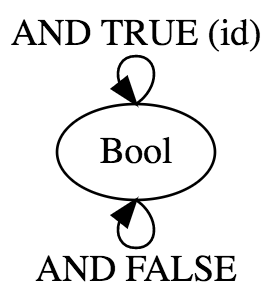
id = (AND True)
id . (AND False) = (AND False)
(AND False) . (AND False) = (AND False)
(AND False) . id = (AND False)
id . id = idRepresent addition modulo 3 as a monoid category.
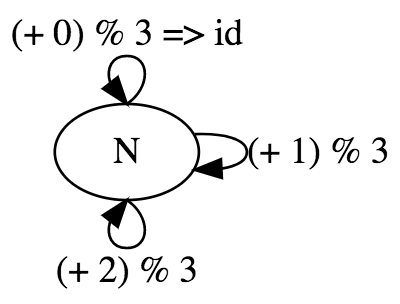
category-theory-for-programmers-103
By Walter Schulze
category-theory-for-programmers-103
- 1,359



