Reactition

REACTITION  

[ree-akt-tish-uhn]

noun 

1 - direct perception of the solvability of an interviewer's white board question given the time constraints 

2 - the application of one's ninja REACTO discernment to either a) solve or b) discard the 'pressure to solve' in favor of demonstrating one's knowledge and ability to reason

3 - a tool deployed by the finest REACTO ninjas to land the job after a single white boarding session

Typical REACTO Scenario: 

1- you meet the interviewer, exchange pleasantries 

2- she/he (surreptitiously) leads you to a white board

3 - she/he presents the problem

4 - you: 'so what I think you're asking is this'; 

5 - interview: 'you got it!'

6- You: 

a) start REACTO-ing

-or- 

b) deploy REACTITION 

REACTITION

YOU WILL BE GIVEN PROBLEMS THAT ARE NOT SOLVABLE IN UNDER AN HOUR

A REAL LIFE EXAMPLE: 

Create a function that takes a partially filled out sudoku board (which can assume the form of any data structure(s) you'd like) and returns a boolean indicating whether the board is a valid sudoku board or not  

REACTITION

THIS IS HARD! 

WHY?

1) The interviewer is asking you to choose the data structure 

2) you have to further fill out the board by inferring necessary states (even if only 20 squares are filled out, the states of those squares may dictate (by inference) that 25 squares are filled out)

REACTITION

1 - Assess the rules 

The Classic Sudoku is a number placing puzzle based on a 9x9 grid with several given numbers. The object is to place the numbers 1 to 9 in the empty squares so that each row, each column and each 3x3 box contains the same number only once.

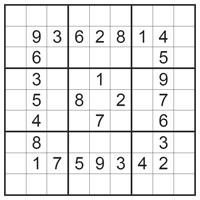
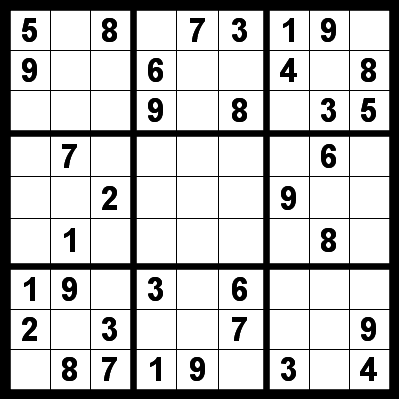
REACTITION

2 - Assess The Steps

a) check each column

b) check each row

c) check each box

d) infer: some of the boxes will not be filled in but will have a determinate value based on the values of other boxes

e) iterate over whatever structure you decide to use and transform the structure at least once

REACTITION

f) choose a REALLY good data structure: 

i) an n-dimensional array? 

ii) hash table mapping keys to linked lists?

iii) hash table mapping keys to arrays?

iv) arrays of hash tables?

g) choose a SMART arrangement of data

what information do you want to store?

a) the number (duh)

b)  the number/node's exact position (column, row, box) ?

c)  a data structure of all the possible values?

REACTITION

1. Careful Consideration of Possible Data Structures (don't immediately choose a 2d array)

2. Guess/Infer Function that infers the determinate values of empty squares

3. Helper Functions: checkRow, checkColumn, checkBox, collectEmptyPositions (show that you know how to break a complex problem into smaller, easier problems)

4. Articulation that creating this function is not the same as solving the board 

 
//arrays of arrays where each array is a box or column or row
[[1, 2, 3, 4, 5, 6, 7, 8, 9], [1, 2, 3, 4, 5, 6, 7, 8, 9]]
 
//array of hashes that maps each number to an array 
//that holds its position as a string
[{1: ['R1', 'C1', 'B!']}]
 


//hash-array combo
{'C1': 
    [
        {
            value: 9,
            position: ['R1', 'B1'],
        }, 
        {
            value: null, 
            position: ['R2', 'B1']
            possibles: [8, 2]
        }
    ]
}

REACTITION

THINGS TO THINK ABOUT

This function must be able to take: 

- an empty board  

- a board that is immediately invalid (two 2's in the same row, column or box)

- how many non-immediately conflicting spaces can be filled for which the board is always valid (pre-inference)

- GUESS FUNCTION: fills in possible values by making inferences based on the initial state of the board

REACTITION

The more you consider the problem, the clearer it should become that the interviewer wants to watch you: 

1 - weigh the pros and cons of various data structures

2 - decide what kinds of information to store on each node 

 3 - discern the various edge cases 

4 - recognize that this algorithm will have to further solve (guessing function) the sudoku before assessing whether it can be solved 

REACTITION

- SAY NO TO FOOLHARDINESS

a) approach is key 

b) great examples lead you to edge cases

c) understand difficulty now not later

- SAY YES TO "UNSOLVABLE" REACTOs

a) show off your stuff

b) drop hot terms: linked list, hash table, binary search trees 

- NOW: present this problem to your fellows and try to get them to deploy REACTITION

REACTITION

SOLUTION

- the sudoku problem is an NP-complete problem: no efficient algorithm exists so far 

- so don't be THAT interviewee ('can do!' and then a cascade of increasingly paralyzing realizations of the complexity of the problem and the thoughtlessness implied by one's 'can do' attitude)

REACTITION

BACKTRACKING

 we select the cell or the constraint with the minimum choices, fix to one number and move forward; when a cell is left with no choice, we go back to the previous step and select the next allowed number. The key to fast solving is to quickly find cells that can be determined with simple logic, including at least the naked single and hidden single rules. 

- across all viable sudoku solvers, data structures vary greatly 

REACTITION

DLX (dancing links): recursive, non-deterministic, depth-first backtracking algorithm that finds all solutions to the exact cover problem (given a collection S of subsets of a set X, an exact cover is a subcollection S* of S such that each element in X is contained in exactly one subset in S*)

example: 

Let  = {N, O, P, E} be a collection of subsets of a set X = {1, 2, 3, 4} such that:

• N = { },
• O = {1, 3},
• P = {2, 3}, and
• E = {2, 4}.

The subcollection {O, E} is an exact cover of X, since the subsets O = {1, 3} and E = {2, 4} are disjoint and their union is X = {1, 2, 3, 4}.

REACTITION

"SOLUTION"

1. saveEmptyPositions: Iterate through the board and save all of the empty positions into an array so we can track which numbers are mutable and keep order to our testing.

2. checkRow, checkColumn, checkBoxSquare, checkValue: Check the column, row, and current 3x3 square for a match to the current value tested, which can all be called with checkValue.

3 - solvePuzzle: Take the parsed Sudoku board and the array of empty positions, and find the solution.

4- solveSudoku: Parse the board, save the empty positions, and pass them to solvePuzzle.