Functional  Programming

by Ayush Goyal

What?

It's a programming style/paradigm

Why?

Results in concise code, easier to reason, less prone to errors

Define What rather than How

Functions without side-effects

A huge focus on Immutability of values

When/Where?

Lets dive into some key concepts

First Class Functions

Functions are values

First Class Functions

#function passed around as value
def multiply_with_3(x):
    return x * 3

mul3 = multiply_with_3
mul3(6)

=> 18


#function returning functions
def multiply_with_x(x):
    def return_func(y):
        return x*y
    return return_func

multiply_with_3 = multiply_with_x(3)

Higher Order Function

Functions can be passed to other functions as they are values

Higher Order Function

#function with function as arguments

def multiply_with_3(x):
    return x * 3

def add5_aftermodify(x,modfyingfunc):
    return modifyingfunc(x) + 5

add5_aftermodify(5,multiply_with_3)
=> 23

Pure Functions

Pure functions are referentialy transparent and without side-effects

Pure Functions

#pure function
def identity(x):
    return x

def square(x):
    return x*x


#impure function
def print_square(x):
    print x*x

import time
def bad_random(x):
    return int(time.time() % (x - 1))
    

Anonymous functions

Create functions on the fly, without assigning names, useful for closures and Higher Order functions

Anonymous Functions

# anonymous function
lambda x: x + 3

# can be binded to value
z = lambda x: x + 3

def less_than_x(threshold):
    return lambda x: x <= threshold

less_than_3 = less_than_x(3)

less_than_3(5)
=> False

less_than_x(3)(5)
=> False

Anonymous Functions

;; in clojure

;; function definition
(defn square[x] (* x x))

;; function bind to variable
(def square (fn [x] (* x x))
 

Awesome Example 1

Awesome Example 1

from math import cos,pi

cube = lambda x: x*x*x

def derivative(func):
    dx = 0.000000001
    return lambda x: (func(x+dx) - func(x))/ dx

print derivative(cube)(2.0)   #=> 12.0000009929
print derivative(cos)(pi/2)   #=> -1.00000008274

deriavative_cube = derivative(cube)

Recursion

Recursion

;;define fibonnaci tree recursion
(define fib 
  (lambda (x) 
    (if (or (= 1 x) (= 0 x)) 
         1
         (+ (fib (- x 1)) (fib (- x 2))))))



;;define fibbonnaci iterative recursion
(define (fib-iter x y i n)
  (if (= i n) 
      y
      (fib-iter y (+ x y) (inc i) n))

(define (fib2 n) (fib-iter 0 1 0 n))

Recursion

;;define fibonnaci tree recursion
(define fib 
  (lambda (x) 
    (if (or (= 1 x) (= 0 x)) 
         1
         (+ (fib (- x 1)) (fib (- x 2))))))

;; tree recursion Fibonacci expansion
(fib 5)
(+ (fib 4) (fib 3))
(+ (+ (fib 3) (fib 2)) (+ (fib 2) (fib 1)) )
(+ (+ (+ (fib 2) (fib 1)) (+ (fib 0) (fib 1))) (+ (+ (fib 0) (fib 1)) 1))
(+ (+ (+ (+ (fib 0) (fib 1)) 1) (+ 1 1)) (+ (+ 1 1) 1))
(+ (+ (+ (+ 1 1) 1) (+ 1 1)) (+ (+ 1 1) 1))  
;#=> 8

Recursion

;;define fibbonnaci iterative recursion
(define (fib-iter x y i n)
  (if (= i n) 
      y
      (fib-iter y (+ x y) (inc i) n))

(define (fib2 n) (fib-iter 0 1 0 n))

;; iterative recursion Fibonacci expansion
(fib2 5)
(fib-iter 0 1 0 5) 
(fib-iter 1 1 1 5) ;; notice that at each step x(1st arg) is replaced with y(2nd arg)
(fib-iter 1 2 2 5) ;; and y is being replaced with sum of x and y
(fib-iter 2 3 3 5)
(fib-iter 3 5 4 5)
(fib-iter 5 8 5 5) ;; fib2 returns y(second arg) if i(third arg) and n(fourth arg) are equal 

;#=> 8

Recursion

Tree Recursion flow

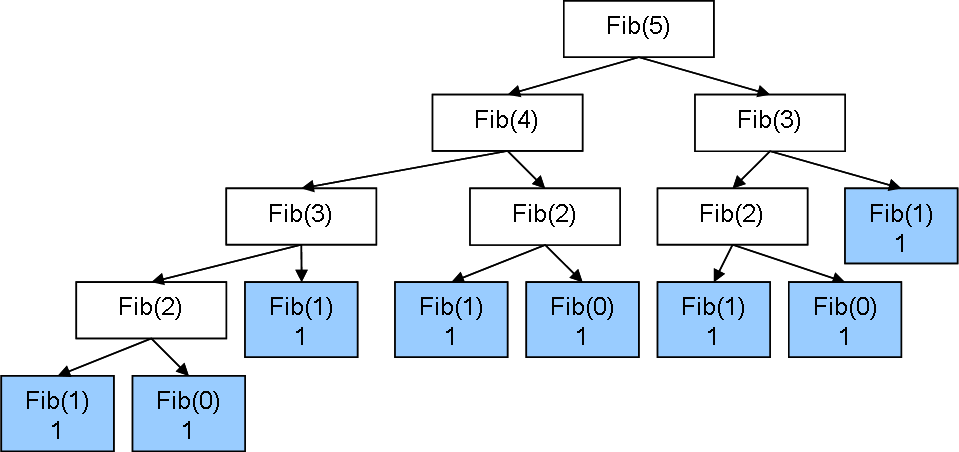
Let's discuss some general higher order functions before moving ahead

Map

# python
# imperative
array = []
for i in range(1,10):
    array.push(x*x)
print array
#=> [1, 4, 9, 16, 25, 36, 49, 64, 81]

# functional
map(lambda x: x*x, range(1,10))
#=> [1, 4, 9, 16, 25, 36, 49, 64, 81]

# ruby
(0..3).map {|x| (Time.now - 86400 * x).strftime("%d-%m-%Y")}
# => ["07-03-2015", "06-03-2015", "05-03-2015", "04-03-2015"]

Reduce

# python

# 1 + 4 + 9 + 16 + 25 ......

# imperative
sum = 0
for i in range(1,10):
     sum = sum + i*i
print sum
#=> 285

# functional
reduce(lambda x,y: x + y , map(lambda x: x*x, range(1,10)))
#=> 285

Filter

# python

# 4 + 16 + 36 + 64 ....

# imperative
sum = 0
for i in range(1,10):
     if i % 2 == 0:
         sum = sum + i*i
print sum
#=> 120

# functional
even   = lambda x: (x % 2 == 0)
sum    = lambda x,y: x + y
square = lambda x: x * x
reduce(sum,map(square,filter(even, range(1,10))))
#=> 120

Sorting

# python

array = ["a","quick","brown","fox"]

sorted(array)
# => ['a', 'brown', 'fox', 'quick']

sorted(array,key = lambda x: len(x))
# => ['a', 'fox', 'quick', 'brown']


import time
dates = ["29-04-2014", "28-04-2014", "21-04-2015"]
sorted(dates,key =  lambda d: time.strptime(d,"%d-%m-%Y"))
# => ['28-04-2014', '29-04-2014', '21-04-2015']

Function Composition

Function Composition

# python
dec = lambda x: x - 1 
inc = lambda x: x + 1
square = lambda x: x*x

def dec_double_inc(x):
    dec(square(inc(x)))

dec_double_inc(4)
=> 10

Function Composition

Function Composition

# python
def compose(*functions):
    return reduce(lambda f,g: lambda x: f(g(x)),functions)

dec = lambda x: x - 1 
inc = lambda x: x + 1
square = lambda x: x*x

inc_square_dec = compose(dec,square,inc)

inc_square_dec(4)
=> 24

Function Composition

;; clojure
(def dec_square_inc (comp inc (fn [x] (* x x)) dec))

-- haskell
dec :: Num a => a -> a
dec a = a - 1

inc :: Numa a => a -> a
inc a = a + 1

square :: Numa a => a -> a
square a = a * a

dec_square_inc = (dec.square.inc)

Lazy Evaluation

Evaluate only when required

Lazy Evaluation

# generator expressions in python
def tokenize_file(path):
    return (word for line in open(path) for word in line.split())

def count_words_in_file(path):
    sum = lambda x,y: x + y
    constant_one = lambda x: 1
    return reduce(sum, map(constant_one,tokenize_file(path)))

# generator function
def drange(start, stop, step):
     r = start
     while r < stop:
        yield r
        r += step

Generator Expressions/Functions in python

Lazy Evaluation

(def fib (map first (iterate (fn [[a b]] [b (+ a b)]) [0 1])))
(take 10 fib)   ;;(0 1 1 2 3 5 8 13 21 34)

(def fib2 (map first (iterate (fn [[a b]] (do (println "processing") [b (+ a b)])) [0 1])))

(take 2 fib2)
;processing
;(0 1)

(take 2 fib2)
;(0 1)

(take 10 fib2)
;processing
;processing
;processing
;processing
;processing
;processing
;processing
;processing
;(0 1 1 2 3 5 8 13 21 34)

(take 11 fib2)
;processing
;(0 1 1 2 3 5 8 13 21 34 55)

Lazy/Infinite Sequences in haskell/clojure

Awesome Example 2

Awesome Example 2

from math import cos,pi

cube = lambda x: x*x*x

def drange(start, stop, step):
     r = start
     while r < stop:
        yield r
        r += step

def integral(func):
    step = lambda a,b: (b-a)/1000.0
    sum  = lambda x,y: x + y
    prod = lambda dx: lambda x: func(x) * dx
    return lambda a,b: reduce(sum ,map( prod(step(a,b)),
                                        drange(a,b,step(a,b))))

print integral(cube)(0,3)      #=> 20.20952025
print integral(cos)(0,pi/2)    #=> 1.00078519255

Currying

mul :: (Num a)=> a -> a -> a
mul x y = x * y

mul_3 = mul 3

mul 5 6
--> 30

mul3 6
--> 18

:t mul
--> mul :: Num a => a -> a -> a

:t mul3
--> mul3 :: Num a => a -> a

-- Of,course you could've just done this
mul3 = (3 *)

Currying

from functools import partial

# emulating currying in python
def multiply(a,b):
    return a*b

multiply_with_3 = partial(multiply,3)
multiply_with_3 = lambda x: multiply(3,x)

Most language don't support currying but there are alternatives

Questions

Resources

• Structure and Interpretation of Computer programs (SICP)
• The value of values and simplicity matters by Rich Hickey (doesn't require programming)
• Learn you a haskell for greater good