Perceptron

Marcelo Finger Alan Barzilay



Objetivo: aprender função f tal que f(x) ≈ y

Regressão: y é ordenado
Classificação: y é categórico
Aprendizado Supervisionado

Dados: conjunto de pares \((x_1,y_1), \dots , (x_N,y_N) \)
onde \(x_i\) é uma entrada d-dimensional \(x_i = (x_{i}^1, x_{i}^2, \dots, x_{i}^d)\), e \(y\) é a variável objetivo
K Nearest Neighboors
Exemplos
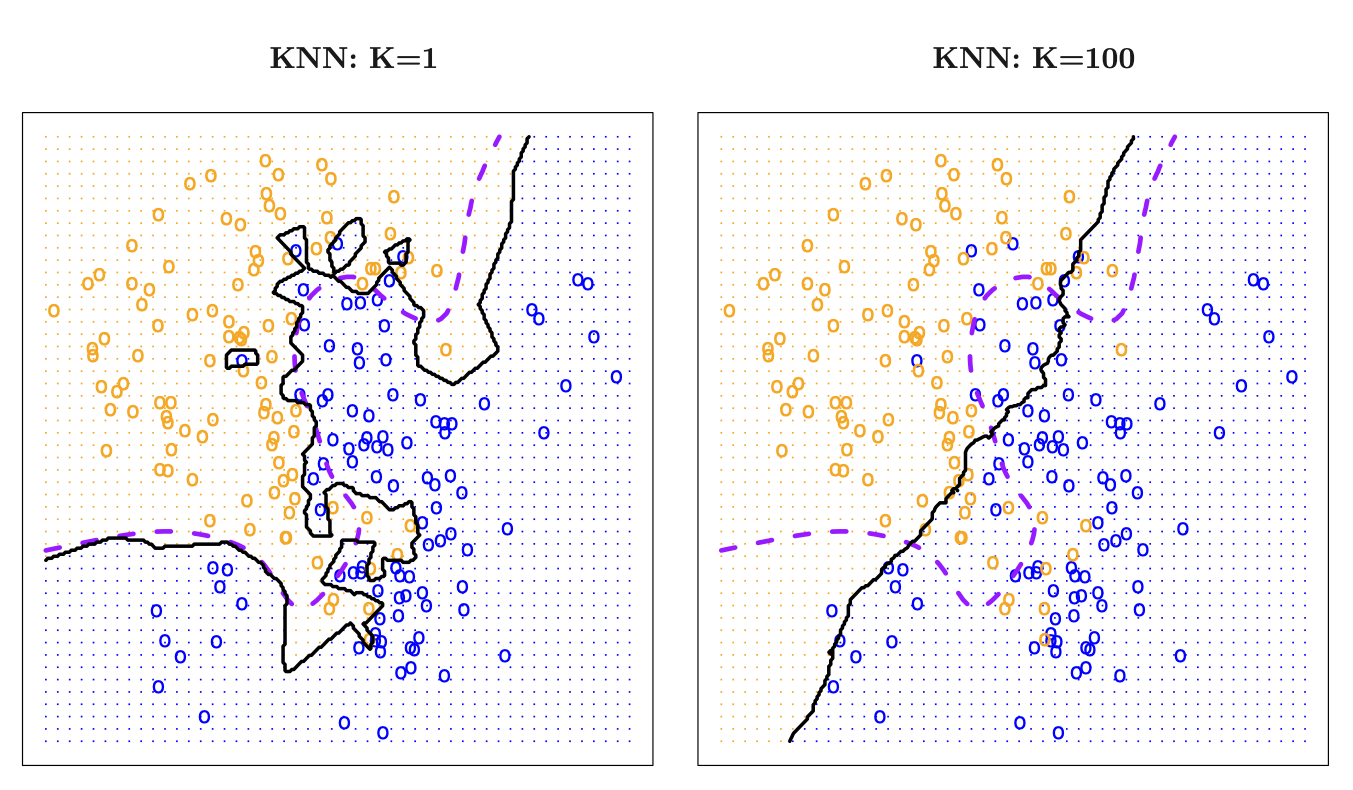
Decision Trees
<a
\(\geq\)a
\(\geq\)b
<b

Classificadores lineares
Perceptron
\ perceptron( w,x) =\begin{cases}
\ \ \ 1 & se\mathrm{,} \ x\cdotp w\ >0\\
-1 & se\mathrm{,} \ x\cdotp w\ < 0
\end{cases}
Classifica pontos de acordo com um hiperplano definido por \(w\)
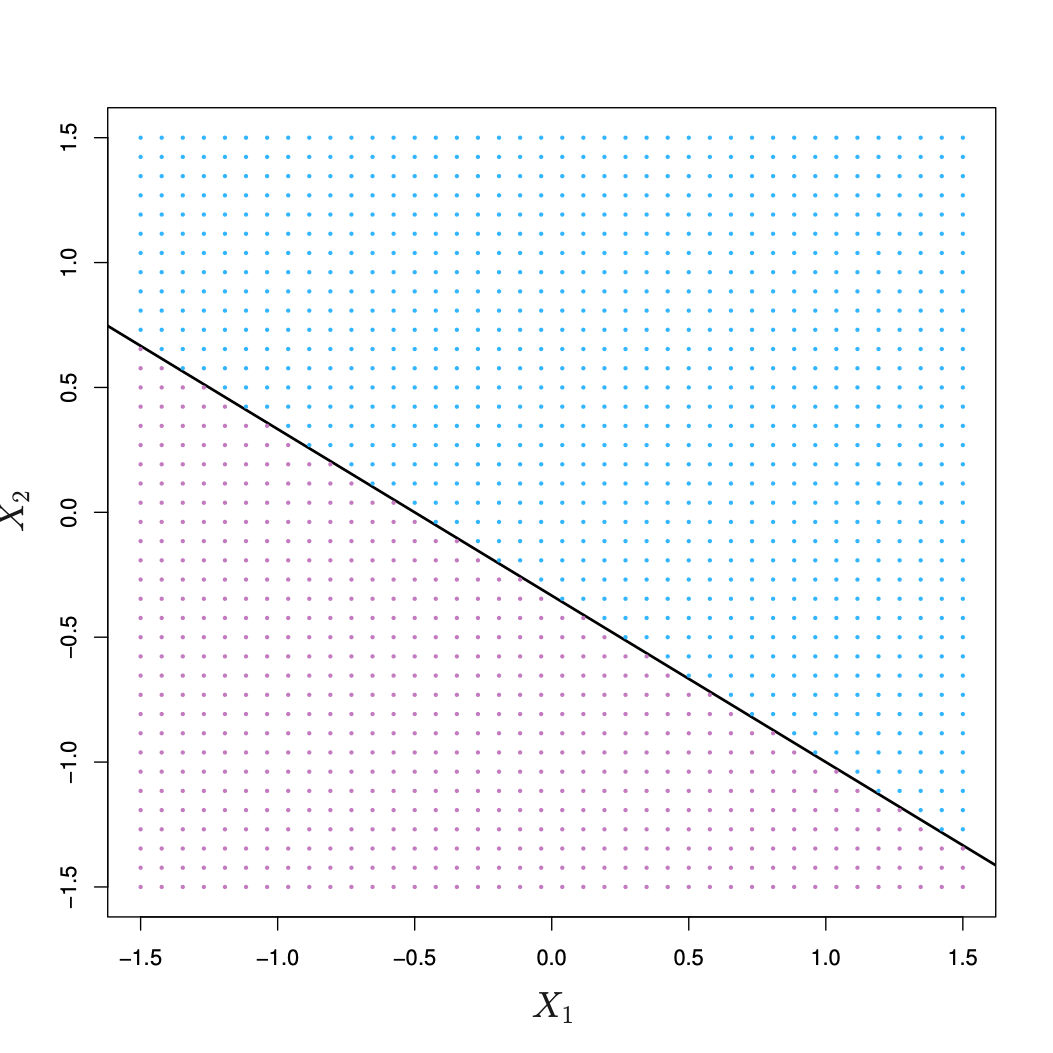

Classificadores lineares
Algoritmo Perceptron
Como escolher um hiperplano para um conjunto de dados?
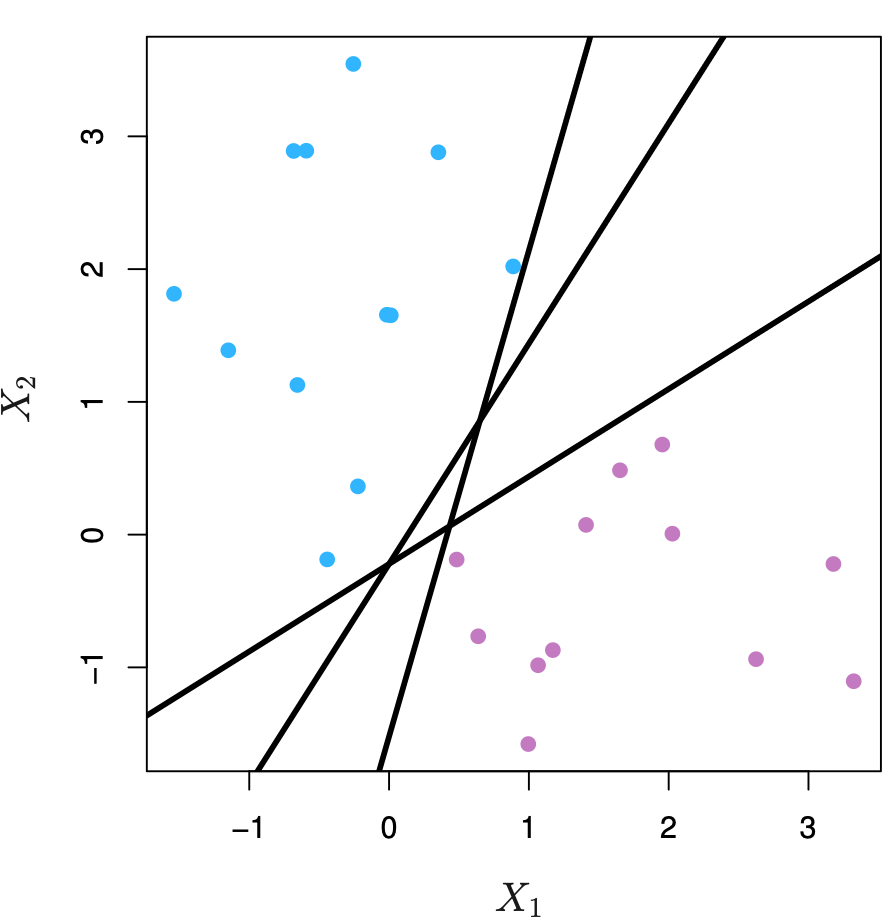

Classificadores lineares
Algoritmo Perceptron

Assumindo que os pontos sejam linearmente separáveis, tome um hiperplano \(w\) aleatório e repita até convergir:
- Escolha um par \((x_i,y_i)\)
- Se \(w\cdotp y_i\cdotp x_i \leq 0\):
- \(w = w + y_i\cdotp x_i\)

Problemas com Perceptron Clássico
- Separabilidade: se dados não são linearmente separáveis o algoritmo não converge
- Margens pequenas: O hiperplano gerado pode ter uma margem baixa o que leva a uma baixa generalização
- Nenhuma medida de confiança
Perceptron
Probabilistico

Proxima aula!

2.1 perceptron
By barzilay
2.1 perceptron
- 105



