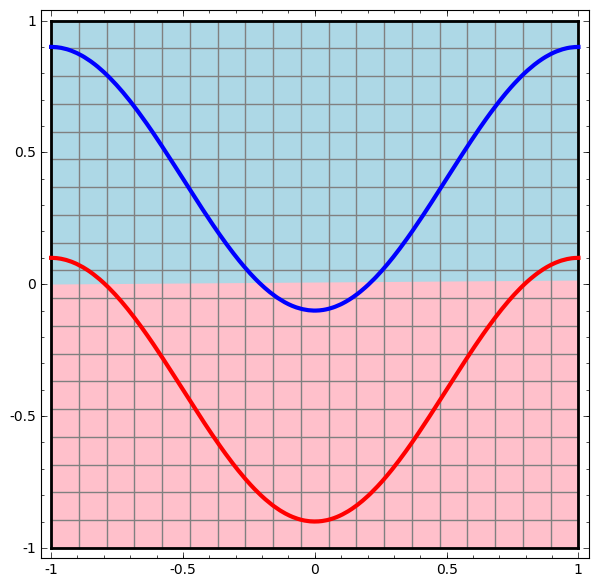
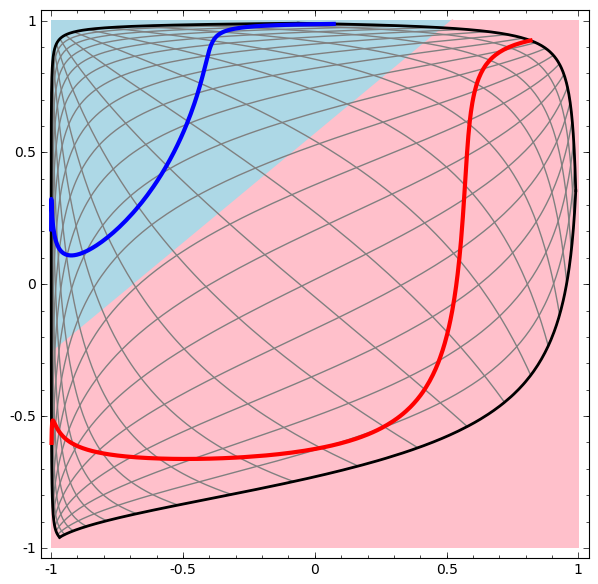
Perceptron Probabilístico
Marcelo Finger Alan Barzilay
Problemas com Perceptron Clássico
- Separabilidade: se dados não são linearmente separáveis o algoritmo não converge
- Margens pequenas: O hiperplano gerado pode ter uma margem baixa o que leva a uma baixa generalização
- Nenhuma medida de confiança
Perceptron Probabilístico
(Regressão Logística)
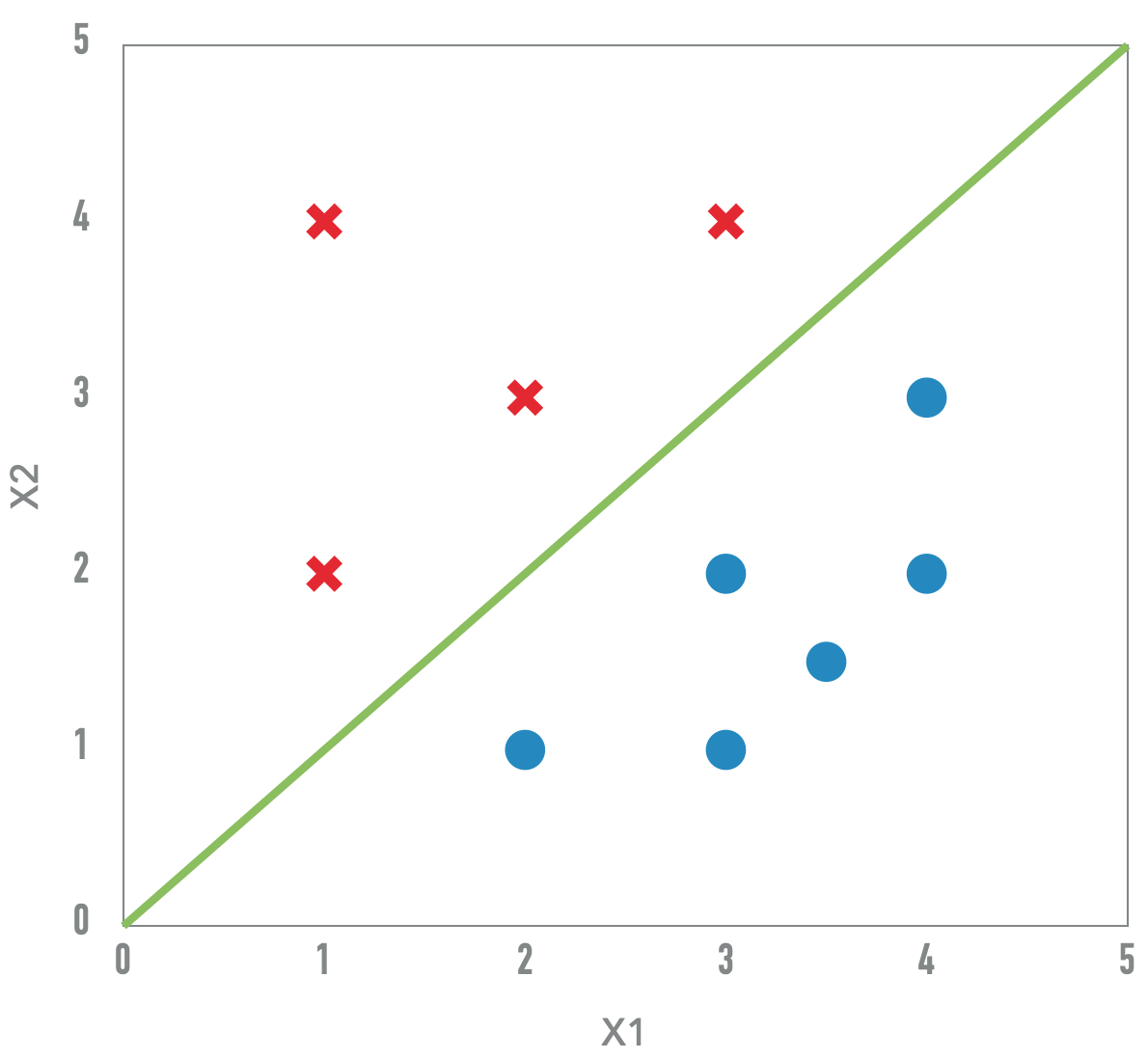
Intuição: Quanto mais longe do hiper plano, maior a confiança na classificação
Perceptron Probabilístico
\Pr( Y=1|x) =0.5
\Pr( Y=1|x) \approx 0
\Pr( Y=1|x) \approx 1
x \cdotp w
Perceptron Probabilístico
\Pr( Y=1|x) =0.5
\Pr( Y=1|x) \approx 0
\Pr( Y=1|x) \approx 1
x \cdotp w
\Pr( Y=y|x) =\frac{1}{1+\ \exp( -y\cdotp w\cdotp x)}
\Pr( Y=1|x)
Dados não linearmente separaveis
XOR
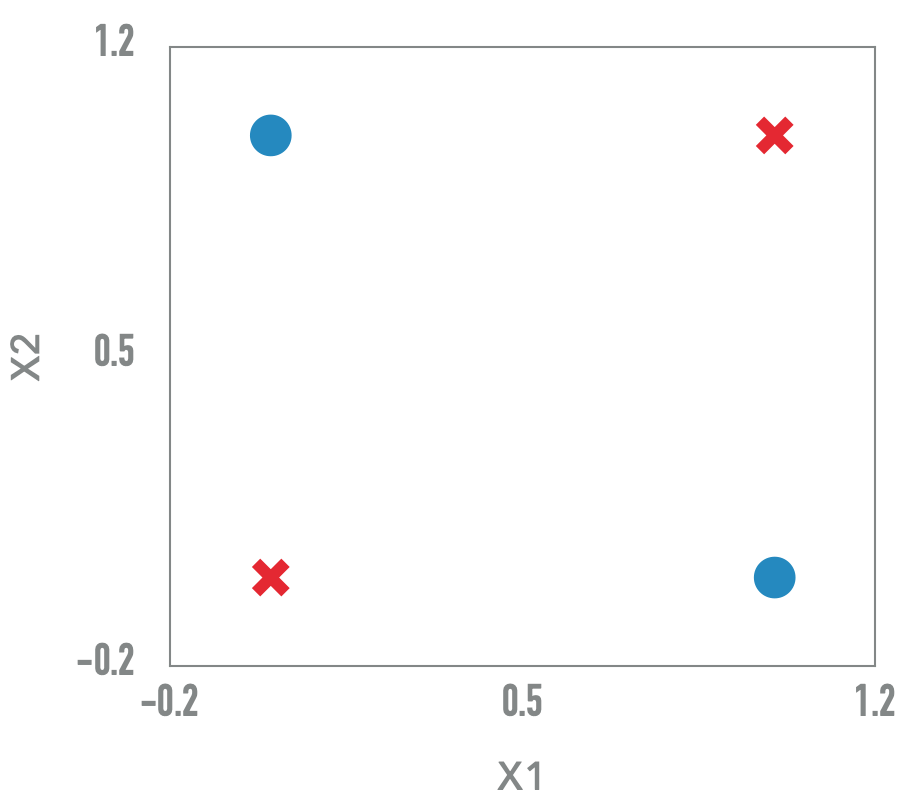
Perceptron Clássico e incapaz de aprender a função booleana XOR
Mas e com 2 hiper-planos?
Perceptron Multicamada
Hornik 1989: Perceptrons multicamada com funções de ativação podem aproximar arbitrariamente bem qualquer função continua
Combinando diferentes perceptrons podemos construir uma rede que resulta em um modelo fundamentalmente mais poderoso
Uma combinação linear de modelos lineares resultará em um modelo linear.
Como introduzir não linearidade?
Funções de ativação
- Sigmoide
Sigmoide
\sigma(x) = \frac{1}{1+e^{-x}}
Funções de ativação
- Sigmoide
- Tanh
Tanh
tanh(x) = \frac{e^x - e^{-x}}{e^x +e^{-x}}
Funções de ativação
- Sigmoide
- Tanh
- ReLU
ReLU
max(0,x)
Funções de ativação
- Sigmoide
- Tanh
- ReLU
- Leaky ReLU
Leaky ReLU
\begin{cases}
0.01x & se\ x \leq 0\\
x & se\ x > 0
\end{cases}
Titulo Proxima Aula
Proxima aula!
2.2 perceptron probabilistico
By barzilay
