A HANDS ON GUIDE TO
DEEP LEARNING
Andrew Beam, PhD
Instructor
Department of Biomedical Informatics
Harvard Medical School
BMI 703 - October 10th, 2018
twitter: @AndrewLBeam
WHY DEEP LEARNING?
DEEP LEARNING HAS MASTERED GO
DEEP LEARNING HAS MASTERED GO
Source: https://deepmind.com/blog/alphago-zero-learning-scratch/
Human data no longer needed
DEEP LEARNING HAS MASTERED GO
DEEP LEARNING HAS MASTERED GO
DEEP LEARNING CAN PLAY VIDEO GAMES
DEEP LEARNING CAN DIAGNOSE PATIENTS
Has the potential to change many medical specialities
DEEP LEARNING CAN DIAGNOSE PATIENTS
Has the potential to change many medical specialities
DEEP LEARNING CAN DIAGNOSE PATIENTS
What does this patient have?
A six-year old boy has a high fever that has lasted for three days. He has extremely red eyes and a rash on the main part of his body in addition to a swollen and red strawberry tongue. Remaining symptoms include swollen lymph nodes in the neck and Irritability
DEEP LEARNING CAN DIAGNOSE PATIENTS
What does this patient have?
A six-year old boy has a high fever that has lasted for three days. He has extremely red eyes and a rash on the main part of his body in addition to a swollen and red strawberry tongue. Remaining symptoms include swollen lymph nodes in the neck and Irritability
Image credit: http://colah.github.io/posts/2015-08-Understanding-LSTMs/
DEEP LEARNING CAN DIAGNOSE PATIENTS
What does this patient have?
A six-year old boy has a high fever that has lasted for three days. He has extremely red eyes and a rash on the main part of his body in addition to a swollen and red strawberry tongue. Remaining symptoms include swollen lymph nodes in the neck and irritability
TRANSFORMING COMPUTATIONAL BIOLOGY
Not just medicine, but genomics too
More here: https://github.com/gokceneraslan/awesome-deepbio
EVERYONE IS USING DEEP LEARNING
WHAT IS A NEURAL NET?
MULTILAYER PERCEPTRONS (MLPs)
- Most generic form of a neural net is the "multilayer perceptron"
- Input undergoes a series of nonlinear transformation before a final classification layer
Image credit: http://cs231n.github.io
NEURAL NETWORKS ARE AN OLD IDEA
One of the very first ideas in machine learning and artificial intelligence
- Date back to 1940s
- Many cycles of boom and bust
- Repeated promises of "true AI" that were unfulfilled followed by "AI winters"
Are today's neural nets any different than their predecessors?
"[The perceptron is] the embryo of an electronic computer that [the Navy] expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence." - Frank Rosenblatt, 1958
MILESTONES
IN THE BEGINNING... (1940s-1960s)
Rosenblatt's Perceptron, 1957
- Initially very promising
- Came with provably correct learning algorithm
- Could recognize letters and numbers
THE FIRST AI WINTER (1969)
Minsky and Papert show that the perceptron can't even solve the XOR problem
Kills research on neural nets for the next 15-20 years
THE BACKPROPAGANDISTS EMERGE (1986)
Rumelhart, Hinton, and Willams show us how to train multilayered neural networks
THE PERCEPTRON AND BACKPROP
Pretend we just have two variables:
x_1,x_2
... and a class label:
y \in \{0,1\}
f(x_1,x_2) := w_0 + x_{i1} * w_1 + x_{i2} * w_2
Pretend we just have two variables:
x_1,x_2
... and a class label:
y \in \{0,1\}
... we construct a function to predict y from x:
THE PERCEPTRON AND BACKPROP
f(x_1,x_2) := w_0 + x_{i1} * w_1 + x_{i2} * w_2
Pretend we just have two variables:
x_1,x_2
... and a class label:
y \in \{0,1\}
... we construct a function to predict y from x:
p(x_1,x_2) := \frac{1}{1+\exp(-f(x_1,x_2))}
... and turn this into a probability using the logistic function:
THE PERCEPTRON AND BACKPROP
f(x_1,x_2) := w_0 + x_{i1} * w_1 + x_{i2} * w_2
Pretend we just have two variables:
x_1,x_2
... and a class label:
y \in \{0,1\}
... we construct a function to predict y from x:
p(x_1,x_2) := \frac{1}{1+\exp(-f(x_1,x_2))}
... and turn this into a probability using the logistic function:
\ell(w|x) := -y*\log(p(x)) - (1-y)*\log(1-p(x))
... and use Bernoulli negative log-likelihood as loss:
THE PERCEPTRON AND BACKPROP
f(x_1,x_2) := w_0 + x_{i1} * w_1 + x_{i2} * w_2
Pretend we just have two variables:
x_1,x_2
... and a class label:
y \in \{0,1\}
... we construct a function to predict y from x:
p(x_1,x_2) := \frac{1}{1+\exp(-f(x_1,x_2))}
... and turn this into a probability using the logistic function:
This is good old-fashioned logistic regression
\ell(w|x) := -y*\log(p(x)) - (1-y)*\log(1-p(x))
... and use Bernoulli negative log-likelihood as loss:
THE PERCEPTRON AND BACKPROP
How do we learn the "best" values for ?
\{w_0,w_1,w_2\}
THE PERCEPTRON AND BACKPROP
How do we learn the "best" values for ?
\{w_0,w_1,w_2\}
Gradient Decscent
- Give weights random initial values
- Evaluate partial derivative of each weight with respect negative log-likelihood at current weight value
- Take a step in direction opposite to the gradient
- Rinse and repeat
THE PERCEPTRON AND BACKPROP
How do we learn the "best" values for ?
\{w_0,w_1,w_2\}
Backprop is how we compute the gradients for our model's parameters. Later we will see why this is important
Gradient Decscent
- Give weights random initial values
- Evaluate partial derivative of each weight with respect negative log-likelihood at current weight value
- Take a step in direction opposite to the gradient
- Rinse and repeat
THE PERCEPTRON AND BACKPROP
NEURAL NET EXERCISE
MLPs AND MODERN NEURAL NETS
LOGISTIC REGRESSION -> MLP
With a small change, we can turn our logistic regression model into a neural net
- Instead of just one linear combination, we are going to take several, each with a different set of weights (called a hidden unit)
- Each linear combination will be followed by a nonlinear activation
- Each of these nonlinear features will be fed into the logistic regression classifier
- All of the weights are learned end-to-end via SGD
MLPs learn a set of nonlinear features directly from data
"Feature learning" is the hallmark of deep learning approachs
MLPs
Increase the depth to increase network capacity
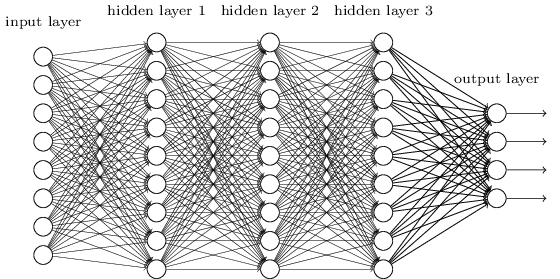
LINEAR ALGEBRA & NEURAL NETS
Essentially all neural nets can be described in terms of a series of matrix multiplications
H_1 = h_1(X) = \phi(X * W_{1})
Input to hidden layer, with 100 hidden units:
where:
- is a matrix of weights
- is matrix containing the activations for all 100 units for each sample and
- is an element-wise activation function
W_1
\phi()
H_1
LINEAR ALGEBRA & NEURAL NETS
Essentially all neural nets can be described in terms of a series of matrix multiplications
H_1 = h_1(X) = \phi(X * W_{1})
Input to hidden layer, with 100 hidden units:
H_2 = h_2(X) = \phi(H_1 * W_{1})
Hidden to hidden layer:
MODERN DEEP LEARNING
Several key advancements have enabled the modern deep learning revolution
Advent of massively parallel computing by GPUs. Enabled training of huge neural nets on extremely large datasets
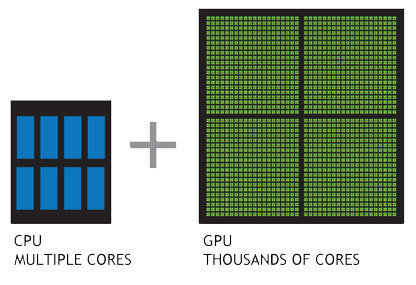
Several key advancements have enabled the modern deep learning revolution
Methodological advancements have made deeper networks easier to train
Architecture
Optimizers
Activation Functions
MODERN DEEP LEARNING
Several key advancements have enabled the modern deep learning revolution
Robust frameworks and abstractions make iteration faster and less error prone
Automatic differentiation allows easy prototyping
MODERN DEEP LEARNING
+
CONVOLUTIONAL NEURAL NETWORKS
CONVOLUTIONAL NEURAL NETS (CNNs)
Dates back to the late 1980s
- Invented by in 1989 Yann Lecun at Bell Labs - "Lenet"
- Integrated into handwriting recognition systems
in the 90s - Huge flurry of activity after the Alexnet paper
THE BREAKTHROUGH (2012)
Imagenet Database
- Millions of labeled images
- Objects in images fall into 1 of a possible 1,000 categories
- Relatively high-resolution
- Bounding boxes giving exact location of object - useful for both classification and localization
Large Scale Visual
Recognition Challenge (ILSVRC)
- Annual Imagenet Challenge starting in 2010
- Successor to smaller PASCAL VOC challenge
- Many tracks including classification and localization
- Standardized training and test set. Competitors upload predictions for test set and are automatically scored
THE BREAKTHROUGH (2012)
Pivotal event occurred in an image recognition contest which brought together 3 critical ingredients for the first time:
- Massive amounts of labeled images
- Training with GPUs
- Methodological innovations that enabled training deeper networks while minimizing overfitting
THE BREAKTHROUGH (2012)
In 2011, a misclassification rate of 25% was near state of the art on ILSVRC
In 2012, Geoff Hinton and two graduate students, Alex Krizhevsky and Ilya Sutskever, entered ILSVRC with one of the first deep neural networks trained on GPUs, now known as "Alexnet"
Result: An error rate of 16%, nearly half what the second place entry was able to achieve.
The computer vision world immediately took notice
THE ILSVRC AFTERMATH (2012-2014)
Alexnet paper has ~ 16,000 citations since being published in 2012!
Q: What was the major flaw with our MLP dog vs. cat classifier?
CONVOLUTIONAL NEURAL NETS (CNNs)
Q: What was the major flaw with our MLP dog vs. cat classifier?
CONVOLUTIONAL NEURAL NETS (CNNs)
What is this a picture of?
Q: What was the major flaw with our MLP dog vs. cat classifier?
CONVOLUTIONAL NEURAL NETS (CNNs)
What is this a picture of?
Q: What was the major flaw with our MLP dog vs. cat classifier?
CONVOLUTIONAL NEURAL NETS (CNNs)
What is this a picture of?
MLPs throw away too much information!
CONVOLUTIONAL NEURAL NETS
Images are just 2D arrays of numbers
Goal is to build f(image) = 1
CONVOLUTIONAL NEURAL NETS
CNNs look at small connected groups of pixels using "filters"
Image credit: http://deeplearning.stanford.edu/wiki/index.php/Feature_extraction_using_convolution
Images have a local correlation structure
Near by pixels are likely to be more similar than pixels that are far away
CNNs exploit this through convolutions of small image patches
CONVOLUTIONAL NEURAL NETS
Example convolution
CONVOLUTIONAL NEURAL NETS
Convolution + pooling + activation = CNN
Image credit: http://cs231n.github.io/convolutional-networks/
CONVOLUTIONAL NEURAL NETS
Pooling provides spatial invariance
Image credit: http://cs231n.github.io/convolutional-networks/
CONVOLUTIONAL NEURAL NETS (CNNs)
CNN formula is relatively simple
Image credit: http://cs231n.github.io/convolutional-networks/
CONVOLUTIONAL NEURAL NETS
Data augmentation mimics the image generative process
Image credit: http://slideplayer.com/slide/8370683/
- Drastically "expands" training set size
- Improves generalization
- Works if it doesn't "break" image -> label relationship
CNN EXERCISE
CNNS AREN'T MAGIC
- Based on solid image priors
- Learns a hierarchical set of filters
- Exploit properties of images, e.g. local correlations and invariances
- Mimic generative distribution with augmentation to reduce over fitting
- Results in end-to-end visual recognition system trained with SGD on GPUs: pixels in -> classifications out
CNNs exploit strong prior information about images
SUMMARY & CONCLUSIONS
DEEP LEARNING AND YOU
Barrier to entry for deep learning is actually low
... but a few things might stand in your way:
- Need to make sure your problem is a good fit
- Lots of labeled data and appropriate signal/noise ratio
- Access to GPUs
- Must "speak the language"
- Many design choices and hyper parameter selections
- Know how to "babysit" the model during learning phase
DEEP LEARNING AND YOU
Barrier to entry for deep learning is actually low
... but a few things might stand in your way:
- Need to make sure your problem is a good fit
- Lots of labeled data and appropriate signal/noise ratio
- Access to GPUs
- Must "speak the language"
- Many design choices and hyper parameter selections
- Know how to "babysit" the model during learning phase
HOW CAN YOU STAY CURRENT?
The field moves fast, staying up to date can be challenging
http://beamandrew.github.io/deeplearning/2017/02/23/deep_learning_101_part1.html
CONCLUSIONS
- Could potentially impact many fields -> understand concepts so you have deep learning "insurance"
- Long history and connections to other models and fields
- Prereqs: Data (lots) + GPUs (more = better)
- Deep learning models are like legos, but you need to know what blocks you have and how they fit together
- Need to have a sense of sensible default parameter values to get started
- "Babysitting" the learning process is a skill
BMI 703 2018
By beamandrew
