DEEP LEARNING
Andrew Beam, PhD
Instructor
Department of Biomedical Informatics
Harvard School of Public Health
November 29th, 2017
twitter: @AndrewLBeam
GOAL OF THIS TALK
SHAMELESS ADVERTISEMENT
We are offering BMI 707 in the spring second session. In this class you will:
- Implement state of the art deep learning models:
- CNNs, RNNs, MLPs, auto encoders, etc
- Learn tensorflow on super fast cloud-based TPUs (tensor processing units)
- Hear guest lectures from leading folks at Google Brain
- Learn how to apply these models to real biomedical data
If you like today's deep learning tapas, sign up for our course and have the full meal
Additional Resources
http://beamandrew.github.io
WHY DEEP LEARNING?
DEEP LEARNING HAS MASTERED GO
DEEP LEARNING HAS MASTERED GO
Source: https://deepmind.com/blog/alphago-zero-learning-scratch/
Human data no longer needed
DEEP LEARNING HAS MASTERED GO
DEEP LEARNING HAS MASTERED GO
DEEP LEARNING CAN DIAGNOSE PATIENTS
Medical imaging already is being changed
DEEP LEARNING CAN DIAGNOSE PATIENTS
Medical imaging already is being changed
DEEP LEARNING CAN DIAGNOSE PATIENTS
What does this patient have?
A six-year old boy has a high fever that has lasted for three days. He has extremely red eyes and a rash on the main part of his body in addition to a swollen and red strawberry tongue. Remaining symptoms include swollen lymph nodes in the neck and Irritability
DEEP LEARNING CAN DIAGNOSE PATIENTS
What does this patient have?
A six-year old boy has a high fever that has lasted for three days. He has extremely red eyes and a rash on the main part of his body in addition to a swollen and red strawberry tongue. Remaining symptoms include swollen lymph nodes in the neck and Irritability
Image credit: http://colah.github.io/posts/2015-08-Understanding-LSTMs/
DEEP LEARNING CAN DIAGNOSE PATIENTS
What does this patient have?
A six-year old boy has a high fever that has lasted for three days. He has extremely red eyes and a rash on the main part of his body in addition to a swollen and red strawberry tongue. Remaining symptoms include swollen lymph nodes in the neck and irritability
EVERYONE IS USING DEEP LEARNING
WHAT IS A NEURAL NET?
WHAT IS A NEURAL NET?
A neural net is made up of 3 things
WHAT IS A NEURAL NET?
A neural net is made up of 3 things
The network structure
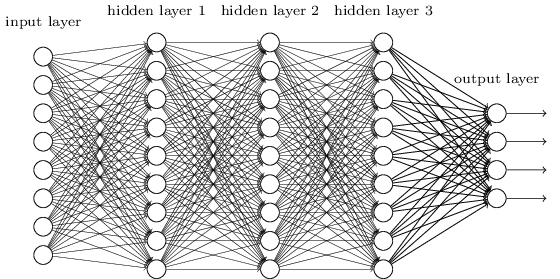
WHAT IS A NEURAL NET?
A neural net is made up of 3 things
The network structure
The loss function
-y_i*\log(p_i) - (1-y_i)*\log(1-p_i)
−yi∗log(pi)−(1−yi)∗log(1−pi)
WHAT IS A NEURAL NET?
A neural net is made up of 3 things
The network structure
The optimizer
The loss function
-y_i*\log(p_i) - (1-y_i)*\log(1-p_i)
−yi∗log(pi)−(1−yi)∗log(1−pi)
NEURAL NETWORK STRUCTURE
NEURAL NET STRUCTURE
A neural net is a modular way to build a classifier
X_1
X1
X_2
X2
Inputs
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
WHAT IS AN ARTIFICIAL NEURON?
The neuron is the basic functional unit a neural network
X_1
X1
X_2
X2
Inputs
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Output
WHAT IS AN ARTIFICIAL NEURON?
The neuron is the basic functional unit a neural network
X_1
X1
X_2
X2
Inputs
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Output
WHAT IS AN ARTIFICIAL NEURON?
The neuron is the basic functional unit a neural network
X_1
X1
X_2
X2
A neuron does two things, and only two things
WHAT IS AN ARTIFICIAL NEURON?
The neuron is the basic functional unit a neural network
X_2
X2
Weight for
X_1
X1
A neuron does two things, and only two things
Weight for
X_2
X2
1) Weighted sum of inputs
w_1*X_1 + w_2*X_2
w1∗X1+w2∗X2
X_1
X1
WHAT IS AN ARTIFICIAL NEURON?
The neuron is the basic functional unit a neural network
X_1
X1
X_2
X2
Weight for
X_1
X1
A neuron does two things, and only two things
Weight for
X_2
X2
1) Weighted sum of inputs
\phi(w_1*X_1 + w_2*X_2)
ϕ(w1∗X1+w2∗X2)
2) Nonlinear transformation
w_1*X_1 + w_2*X_2
w1∗X1+w2∗X2
WHAT IS AN ARTIFICIAL NEURON?
\phi()
ϕ()
is known as the activation function, and there are many choices
Sigmoid
Hyperbolic Tangent
WHAT IS AN ARTIFICIAL NEURON?
Summary: A neuron produces a single number that is a nonlinear transformation of its input connections
X_1
X1
X_2
X2
A neuron does two things, and only two things
= a number
NEURAL NETWORK STRUCTURE
X_1
X1
X_2
X2
Inputs
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Neural nets are organized into layers
NEURAL NETWORK STRUCTURE
X_1
X1
X_2
X2
Inputs
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Input Layer
Neural nets are organized into layers
NEURAL NETWORK STRUCTURE
X_1
X1
X_2
X2
Inputs
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Neural nets are organized into layers
1st Hidden Layer
Input Layer
NEURAL NETWORK STRUCTURE
X_1
X1
X_2
X2
Inputs
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Neural nets are organized into layers
A single hidden unit
1st Hidden Layer
Input Layer
NEURAL NETWORK STRUCTURE
X_1
X1
X_2
X2
Inputs
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Input Layer
Neural nets are organized into layers
1st Hidden Layer
A single hidden unit
2nd Hidden Layer
NEURAL NETWORK STRUCTURE
X_1
X1
X_2
X2
Inputs
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Input Layer
Neural nets are organized into layers
1st Hidden Layer
A single hidden unit
2nd Hidden Layer
Output Layer
LOSS FUNCTIONS
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Output Layer
We need a way to measure how well the network is performing, e.g. is it making good predictions?
LOSS FUNCTIONS
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Output Layer
We need a way to measure how well the network is performing, e.g. is it making good predictions?
Loss function: A function that returns a single number which indicates how closely a prediction matches the ground truth label
LOSS FUNCTIONS
Output
Pr(y = 1 | X_1, X_2)
Pr(y=1∣X1,X2)
Output Layer
We need a way to measure how well the network is performing, e.g. is it making good predictions?
small loss = good
big loss = bad
Loss function: A function that returns a single number which indicates how closely a prediction matches the ground true label
LOSS FUNCTIONS
A classic loss function for binary classification is binary cross-entropy
\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)
ℓ(yi,pi)=−yi∗log(pi)−(1−yi)∗log(1−pi)
LOSS FUNCTIONS
A classic loss function for binary classification is binary cross-entropy
\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)
ℓ(yi,pi)=−yi∗log(pi)−(1−yi)∗log(1−pi)
| y | p | Loss |
|---|---|---|
| 0 | 0.1 | 0.1 |
| 0 | 0.9 | 2.3 |
| 1 | 0.1 | 2.3 |
| 1 | 0.9 | 0.1 |
OUTPUT LAYER & LOSS
Output Layer
The output layer needs to "match" the loss function
- Correct shape
- Correct scale
\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)
ℓ(yi,pi)=−yi∗log(pi)−(1−yi)∗log(1−pi)
OUTPUT LAYER & LOSS
Output Layer
The output layer needs to "match" the loss function
For binary cross-entropy, network needs to produce a single probability
\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)
ℓ(yi,pi)=−yi∗log(pi)−(1−yi)∗log(1−pi)
OUTPUT LAYER & LOSS
Output Layer
The output layer needs to "match" the loss function
One unit in output layer to represent this probability
\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)
ℓ(yi,pi)=−yi∗log(pi)−(1−yi)∗log(1−pi)
For binary cross-entropy, network needs to produce a single probability
OUTPUT LAYER & LOSS
Output Layer
The output layer needs to "match" the loss function
One unit in output layer to represent this probability
\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)
ℓ(yi,pi)=−yi∗log(pi)−(1−yi)∗log(1−pi)
For binary cross-entropy, network needs to produce a single probability
Activation function must "squash" output to be between 0 and 1
OUTPUT LAYER & LOSS
Output Layer
The output layer needs to "match" the loss function
One unit in output layer to represent this probability
\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)
ℓ(yi,pi)=−yi∗log(pi)−(1−yi)∗log(1−pi)
For binary cross-entropy, network needs to produce a single probability
Activation function must "squash" output to be between 0 and 1
We can change the output layer & loss to model many different kinds of data
- Multiple classes
- Continuous response (i.e. regression)
- Survival data
- Combinations of the above
THE OPTIMIZER
Question:
Now that we have specified:
- A network
- Loss function
How do we find the values for the weights that gives us the smallest possible value for the loss function?
How do we minimize the loss function?
Stochastic Gradient Decscent
- Give weights random initial values
- Evaluate partial derivative of each weight with respect negative log-likelihood at current weight value on a mini-batch
- Take a step in direction opposite to the gradient
- Rinse and repeat
THE OPTIMIZER
How do we minimize the loss function?
THE OPTIMIZER
Many variations on basic idea of SGD are available
MODERN NEURAL NETS
MODERN DEEP LEARNING
Several key advancements have enabled the modern deep learning revolution
Advent of massively parallel computing by GPUs. Enabled training of huge neural nets on extremely large datasets
MODERN DEEP LEARNING
Several key advancements have enabled the modern deep learning revolution
Advent of massively parallel computing by GPUs. Enabled training of huge neural nets on extremely large datasets
Several key advancements have enabled the modern deep learning revolution
Methodological advancements have made deeper networks easier to train
Architecture
Optimizers
Activation Functions
MODERN DEEP LEARNING
Several key advancements have enabled the modern deep learning revolution
Robust frameworks and abstractions make iteration faster and less error prone
Automatic differentiation allows easy prototyping
MODERN DEEP LEARNING
+
NEURAL NETS FROM A STATISTICAL PERSPECTIVE
NEURAL NETS
- Neural nets can look strange until you internalize the jargon and what they are doing
- Related to several well-known statistical models
- Misconception: Neural nets work because they are super flexible black boxes
- Reality: Neural nets works because they allow you to incorporate problem-specific constraints very easily and they scale really well
WHY DOES DEEP LEARNING WORK?
https://simplystatistics.org/2017/05/31/deeplearning-vs-leekasso/
WHY DOES DEEP LEARNING WORK?
https://simplystatistics.org/2017/05/31/deeplearning-vs-leekasso/
WHY DOES DEEP LEARNING WORK?
http://beamandrew.github.io/deeplearning/2017/06/04/deep_learning_works.html
WHY DOES DEEP LEARNING WORK?
http://beamandrew.github.io/deeplearning/2017/06/04/deep_learning_works.html
NEURAL NETS REVISITED
Neural nets are always presented in terms of units and layers, but everything can be written in terms of matrix multiplications and element wise operations
NEURAL NETS REVISITED
Neural nets are always presented in terms of units and layers, but everything can be written in terms of matrix multiplications and element wise operations
Recall, a hidden layer does a linear rotation, followed by a nonlinear element-wise transformation
NEURAL NETS REVISITED
Neural nets are always presented in terms of units and layers, but everything can be written in terms of matrix multiplications and element wise operations
Recall, a hidden layer does a linear rotation, followed by a nonlinear element-wise transformation
Given
X_{nxp}, W_{pxh}
Xnxp,Wpxh
NEURAL NETS REVISITED
Neural nets are always presented in terms of units and layers, but everything can be written in terms of matrix multiplications and element wise operations
Recall, a hidden layer does a linear rotation, followed by a nonlinear element-wise transformation
Given
Hidden layer is
X_{nxp}, W_{pxh}
Xnxp,Wpxh
H(X) = \phi(XW)
H(X)=ϕ(XW)
NEURAL NETS REVISITED
Neural nets are always presented in terms of units and layers, but everything can be written in terms of matrix multiplications and element wise operations
Recall, a hidden layer does a linear rotation, followed by a nonlinear element-wise transformation
Given
Hidden layer is
Output layer is
X_{nxp}, W_{pxh}
Xnxp,Wpxh
H(X) = \phi(XW)
H(X)=ϕ(XW)
p(y=1|X) = \frac{1}{1+exp(-H(X))}
p(y=1∣X)=1+exp(−H(X))1
NEURAL NETS REVISITED
A network with two hidden layers is:
H_1(X) = \phi(XW_1)
H1(X)=ϕ(XW1)
H_2(X) = \phi(H_1W_2)
H2(X)=ϕ(H1W2)
p(y=1|X) = \frac{1}{1+exp(-H_2(X))}
p(y=1∣X)=1+exp(−H2(X))1
NEURAL NETS REVISITED
A network with two hidden layers is:
H_1(X) = \phi(XW_1)
H1(X)=ϕ(XW1)
H_2(X) = \phi(H_1W_2)
H2(X)=ϕ(H1W2)
p(y=1|X) = \frac{1}{1+exp(-H_2(X))}
p(y=1∣X)=1+exp(−H2(X))1
In general, layers represent a recursive relationship:
H_t(X) = \phi(H_{t-1}W_t)
Ht(X)=ϕ(Ht−1Wt)
NEURAL NETS REVISITED
Some connections to other models:
- A neural net with no hidden layers = logistic regression
- "Neurons" are really simple, but really weird basis functions
Closely related to generalized additive models (GAM), especially projection pursuit regression (Friedman, 1981)
- Bayesian neural networks: Normal prior on each weight, as number of hidden units -> infinity you recover a Gaussian process (Neal, 1996)
NEURAL NETS REVISITED
So what's the big deal?
NEURAL NETS REVISITED
So what's the big deal?
- Neural nets offer many key advantages in computation, optimization, and regularization
NEURAL NETS REVISITED
So what's the big deal?
- Neural nets offer many key advantages in computation, optimization, and regularization
- Computation: GPUs are exceedingly good at linear algebra -> train big models fast
NEURAL NETS REVISITED
So what's the big deal?
- Neural nets offer many key advantages in computation, optimization, and regularization
- Computation: GPUs are exceedingly good at linear algebra -> train big models fast
- Optimization: Variants of SGD "work" very well on a variety of networks and problems
NEURAL NETS REVISITED
So what's the big deal?
- Neural nets offer many key advantages in computation, optimization, and regularization
- Computation: GPUs are exceedingly good at linear algebra -> train big models fast
- Optimization: Variants of SGD "work" very well on a variety of networks and problems
- Regularization: Neural nets are regularized in dozens of ways explicitly and implicitly to reduce variance
Regularization
REGULARIZATION
Neural nets represent the following optimization problem:
\text{argmin}_{W} \ \ell(y, f(X))
argminW ℓ(y,f(X))
where
f(X) = \frac{1}{1+exp(-\phi(XW))}
f(X)=1+exp(−ϕ(XW))1
REGULARIZATION
A familiar way to regularize is introduce penalties and change
\text{argmin}_{W} \ \ell(y, f(X))
argminW ℓ(y,f(X))
REGULARIZATION
A familiar why to regularize is introduce penalties and change
\text{argmin}_{W} \ \ell(y, f(X))
argminW ℓ(y,f(X))
to
\text{argmin}_{W} \ \ell(y, f(X)) + \lambda R(W)
argminW ℓ(y,f(X))+λR(W)
REGULARIZATION
A familiar why to regularize is introduce penalties and change
\text{argmin}_{W} \ \ell(y, f(X))
argminW ℓ(y,f(X))
to
\text{argmin}_{W} \ \ell(y, f(X)) + \lambda R(W)
argminW ℓ(y,f(X))+λR(W)
where R(W) is often the L1 or L2 norm of W. These are the well known ridge and LASSO penalties, referred to as weight decay by neural net community
STOCHASTIC REGULARIZATION
Often, we will inject noise into the neural network during training. By far the most popular way to do this is dropout
STOCHASTIC REGULARIZATION
Often, we will inject noise into the neural network during training. By far the most popular way to do this is dropout
Given a hidden layer H(X), we are going to set each element of H(X) to 0 with probability p each SGD update.
STOCHASTIC REGULARIZATION
One way to think of this is the network is trained by bagged versions of the network. Bagging reduces variance.
STOCHASTIC REGULARIZATION
One way to think of this is the network is trained by bagged versions of the network. Bagging reduces variance.
Others have argued this is an approximate Bayesian model
STOCHASTIC REGULARIZATION
Many have argued that SGD itself provides regularization
STOCHASTIC REGULARIZATION
http://www.inference.vc/
INITIALIZATION REGULARIZATION
The weights in a neural network are given random values initially
INITIALIZATION REGULARIZATION
The weights in a neural network are given random values initially
There is an entire literature on the best way to do this initialization
INITIALIZATION REGULARIZATION
The weights in a neural network are given random values initially
There is an entire literature on the best way to do this initialization
- Normal
- Truncated Normal
- Uniform
- Orthogonal
- Scaled by number of connections
- etc
INITIALIZATION REGULARIZATION
Try to "bias" the model into initial configurations that are easier to train
INITIALIZATION REGULARIZATION
Try to "bias" the model into initial configurations that are easier to train
Very popular way is to do transfer learning
INITIALIZATION REGULARIZATION
Try to "bias" the model into initial configurations that are easier to train
Very popular way is to do transfer learning
Train model on auxiliary task where lots of data is available
INITIALIZATION REGULARIZATION
Try to "bias" the model into initial configurations that are easier to train
Very popular way is to do transfer learning
Train model on auxiliary task where lots of data is available
Use final weight values from previous task as initial values and "fine tune" on primary task
STRUCTURAL REGULARIZATION
However, the key advantage of neural nets is the ability to easily include properties of the data directly into the model through the network's structure
Convolutional neural networks (CNNs) are a prime example of this
CONVOLUTIONAL NEURAL NETWORKS
CONVOLUTIONAL NEURAL NETS (CNNs)
Dates back to the late 1980s
- Invented by in 1989 Yann Lecun at Bell Labs - "Lenet"
- Integrated into handwriting recognition systems
in the 90s - Huge flurry of activity after the Alexnet paper
THE BREAKTHROUGH (2012)
Imagenet Database
- Millions of labeled images
- Objects in images fall into 1 of a possible 1,000 categories
- Relatively high-resolution
- Bounding boxes giving exact location of object - useful for both classification and localization
Large Scale Visual
Recognition Challenge (ILSVRC)
- Annual Imagenet Challenge starting in 2010
- Successor to smaller PASCAL VOC challenge
- Many tracks including classification and localization
- Standardized training and test set. Competitors upload predictions for test set and are automatically scored
THE BREAKTHROUGH (2012)
In 2011, a misclassification rate of 25% was near state of the art on ILSVRC
In 2012, Geoff Hinton and two graduate students, Alex Krizhevsky and Ilya Sutskever, entered ILSVRC with one of the first deep neural networks trained on GPUs, now known as "Alexnet"
Result: An error rate of 16%, nearly half what the second place entry was able to achieve.
The computer vision world immediately took notice
THE ILSVRC AFTERMATH (2012-2014)
Alexnet paper has ~ 16,000 citations since being published in 2012!
Most algorithms expect "tabular" data
WHY CNNS WORK
| y | X1 | X2 | X3 | X4 |
|---|---|---|---|---|
| 0 | 7 | 52 | 17 | 654 |
| 0 | 23 | 2752 | 4 | 1 |
| 1 | 786 | 27 | 0 | 5 |
| 0 | 354 | 7527 | 89 | 68 |
The problem with tabular data
What is this a picture of?
WHY CNNS WORK
What is this a picture of?
The problem with tabular data
WHY CNNS WORK
What is this a picture of?
Tabular data throws away too much information!
The problem with tabular data
WHY CNNS WORK
CONVOLUTIONAL NEURAL NETS
Images are just 2D arrays of numbers
Goal is to build f(image) = 1
CONVOLUTIONAL NEURAL NETS
CNNs look at small connected groups of pixels using "filters"
Image credit: http://deeplearning.stanford.edu/wiki/index.php/Feature_extraction_using_convolution
Images have a local correlation structure
Near by pixels are likely to be more similar than pixels that are far away
CNNs exploit this through convolutions of small image patches
CONVOLUTIONAL NEURAL NETS
Example convolution
CONVOLUTIONAL NEURAL NETS
Pooling provides spatial invariance
Image credit: http://cs231n.github.io/convolutional-networks/
CONVOLUTIONAL NEURAL NETS
Convolution + pooling + activation = CNN
Image credit: http://cs231n.github.io/convolutional-networks/
CONVOLUTIONAL NEURAL NETS (CNNs)
CNN formula is relatively simple
Image credit: http://cs231n.github.io/convolutional-networks/
CONVOLUTIONAL NEURAL NETS
Data augmentation mimics the image generative process
Image credit: http://slideplayer.com/slide/8370683/
- Drastically "expands" training set size
- Improves generalization
- Works if it doesn't "break" image -> label relationship
WHY DO CNNs WORK SO WELL?
- Based on solid image priors
- Exploit properties of images, e.g. local correlations and invariances
- Mimic generative distribution with augmentation to reduce over fitting
- Results in end-to-end visual recognition system trained with SGD on GPUs: pixels in -> classifications out
CNNs exploit strong prior information about images
SUMMARY & CONCLUSIONS
DEEP LEARNING AND YOU
Barrier to entry for deep learning is actually low
... but a few things might stand in your way:
- Need to make sure your problem is a good fit
- Lots of labeled data and appropriate signal/noise ratio
- Access to GPUs
- Must "speak the language"
- Many design choices and hyper parameter selections
- Know how to "babysit" the model during learning phase
CONCLUSIONS
- Could potentially impact many fields -> understand concepts so you have deep learning "insurance"
- Many connections to other models
- Prereqs: Data (lots) + GPUs (more = better)
- Easy incorporate problem structure directly into model
- Drastic amounts of regularization
- Deep learning models are like legos, but you need to know what blocks you have and how they fit together
DEEP LEARNING Andrew Beam, PhD Instructor Department of Biomedical Informatics Harvard School of Public Health November 29th, 2017 twitter: @AndrewLBeam
BST 235
By beamandrew
BST 235
- 1,970
