DEEP LEARNING

Andrew Beam, PhD

Instructor

Department of Biomedical Informatics

Harvard School of Public Health

October 25th, 2017

twitter: @AndrewLBeam

GOAL OF THIS TALK

SHAMELESS ADVERTISEMENT

We are offering BMI 707 in the spring second session. In this class you will:

Implement state of the art deep learning models:
- CNNs, RNNs, MLPs, auto encoders, etc
Learn tensorflow on super fast cloud-based TPUs (tensor processing units)
Hear guest lectures from leading folks at Google Brain
Learn how to apply these models to real biomedical data

If you like today's deep learning tapas, sign up for our course and have the full meal

Additional Resources

http://beamandrew.github.io

WHY DEEP LEARNING?

DEEP LEARNING HAS MASTERED GO

Source: https://deepmind.com/blog/alphago-zero-learning-scratch/

Human data no longer needed

DEEP LEARNING HAS MASTERED GO

DEEP LEARNING CAN DIAGNOSE PATIENTS

Medical imaging already is being changed

DEEP LEARNING CAN DIAGNOSE PATIENTS

Medical imaging already is being changed

DEEP LEARNING FOR TB DRUG RESISTANCE

Inferring drug-resistance status in tuberculosis from sequence data using deep learning

Joint work with: Michael Chen, Maha Farat

DEEP LEARNING CAN DIAGNOSE PATIENTS

What does this patient have?

A six-year old boy has a high fever that has lasted for three days. He has extremely red eyes and a rash on the main part of his body in addition to a swollen and red strawberry tongue. Remaining symptoms include swollen lymph nodes in the neck and Irritability

DEEP LEARNING CAN DIAGNOSE PATIENTS

What does this patient have?

Image credit: http://colah.github.io/posts/2015-08-Understanding-LSTMs/

DEEP LEARNING CAN DIAGNOSE PATIENTS

What does this patient have?

EVERYONE IS USING DEEP LEARNING

WHAT IS A NEURAL NET?

A neural net is made up of 3 things

WHAT IS A NEURAL NET?

A neural net is made up of 3 things

The network structure

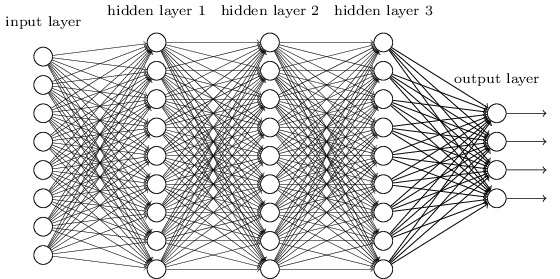
WHAT IS A NEURAL NET?

A neural net is made up of 3 things

The network structure

The loss function

-y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

-y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

WHAT IS A NEURAL NET?

A neural net is made up of 3 things

The network structure

The optimizer

The loss function

-y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

-y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

NEURAL NETWORK STRUCTURE

NEURAL NET STRUCTURE

A neural net is a modular way to build a classifier

X_1

X_1

X_2

X_2

Inputs

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

WHAT IS AN ARTIFICIAL NEURON?

The neuron is the basic functional unit a neural network

X_1

X_1

X_2

X_2

Inputs

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Output

WHAT IS AN ARTIFICIAL NEURON?

The neuron is the basic functional unit a neural network

X_1

X_1

X_2

X_2

Inputs

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Output

WHAT IS AN ARTIFICIAL NEURON?

The neuron is the basic functional unit a neural network

X_1

X_1

X_2

X_2

A neuron does two things, and only two things

WHAT IS AN ARTIFICIAL NEURON?

The neuron is the basic functional unit a neural network

X_2

X_2

Weight for

X_1

X_1

A neuron does two things, and only two things

Weight for

X_2

X_2

1) Weighted sum of inputs

w_1*X_1 + w_2*X_2

w_1*X_1 + w_2*X_2

X_1

X_1

WHAT IS AN ARTIFICIAL NEURON?

The neuron is the basic functional unit a neural network

X_1

X_1

X_2

X_2

Weight for

X_1

X_1

A neuron does two things, and only two things

Weight for

X_2

X_2

1) Weighted sum of inputs

\phi(w_1*X_1 + w_2*X_2)

\phi(w_1*X_1 + w_2*X_2)

2) Nonlinear transformation

w_1*X_1 + w_2*X_2

w_1*X_1 + w_2*X_2

WHAT IS AN ARTIFICIAL NEURON?

\phi()

\phi()

is known as the activation function, and there are many choices

Sigmoid

Hyperbolic Tangent

WHAT IS AN ARTIFICIAL NEURON?

Summary: A neuron produces a single number that is a nonlinear transformation of its input connections

X_1

X_1

X_2

X_2

A neuron does two things, and only two things

= a number

NEURAL NETWORK STRUCTURE

X_1

X_1

X_2

X_2

Inputs

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Neural nets are organized into layers

NEURAL NETWORK STRUCTURE

X_1

X_1

X_2

X_2

Inputs

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Input Layer

Neural nets are organized into layers

NEURAL NETWORK STRUCTURE

X_1

X_1

X_2

X_2

Inputs

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Neural nets are organized into layers

1st Hidden Layer

Input Layer

NEURAL NETWORK STRUCTURE

X_1

X_1

X_2

X_2

Inputs

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Neural nets are organized into layers

A single hidden unit

1st Hidden Layer

Input Layer

NEURAL NETWORK STRUCTURE

X_1

X_1

X_2

X_2

Inputs

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Input Layer

Neural nets are organized into layers

1st Hidden Layer

A single hidden unit

2nd Hidden Layer

NEURAL NETWORK STRUCTURE

X_1

X_1

X_2

X_2

Inputs

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Input Layer

Neural nets are organized into layers

1st Hidden Layer

A single hidden unit

2nd Hidden Layer

Output Layer

LOSS FUNCTIONS

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Output Layer

We need a way to measure how well the network is performing, e.g. is it making good predictions?

LOSS FUNCTIONS

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Output Layer

We need a way to measure how well the network is performing, e.g. is it making good predictions?

Loss function: A function that returns a single number which indicates how closely a prediction matches the ground truth label

LOSS FUNCTIONS

Output

Pr(y = 1 | X_1, X_2)

Pr(y = 1 | X_1, X_2)

Output Layer

We need a way to measure how well the network is performing, e.g. is it making good predictions?

small loss = good

big loss = bad

Loss function: A function that returns a single number which indicates how closely a prediction matches the ground true label

LOSS FUNCTIONS

A classic loss function for binary classification is binary cross-entropy

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

LOSS FUNCTIONS

A classic loss function for binary classification is binary cross-entropy

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

y	p	Loss
0	0.1	0.1
0	0.9	2.3
1	0.1	2.3
1	0.9	0.1

OUTPUT LAYER & LOSS

Output Layer

The output layer needs to "match" the loss function

- Correct shape

- Correct scale

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

OUTPUT LAYER & LOSS

Output Layer

The output layer needs to "match" the loss function

For binary cross-entropy, network needs to produce a single probability

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

OUTPUT LAYER & LOSS

Output Layer

The output layer needs to "match" the loss function

One unit in output layer to represent this probability

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

For binary cross-entropy, network needs to produce a single probability

OUTPUT LAYER & LOSS

Output Layer

The output layer needs to "match" the loss function

One unit in output layer to represent this probability

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

For binary cross-entropy, network needs to produce a single probability

Activation function must "squash" output to be between 0 and 1

OUTPUT LAYER & LOSS

Output Layer

The output layer needs to "match" the loss function

One unit in output layer to represent this probability

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

\ell(y_i,p_i) = -y_i*\log(p_i) - (1-y_i)*\log(1-p_i)

For binary cross-entropy, network needs to produce a single probability

Activation function must "squash" output to be between 0 and 1

We can change the output layer & loss to model many different kinds of data

- Multiple classes

- Continuous response (i.e. regression)

- Survival data

- Combinations of the above

THE OPTIMIZER

Question:

Now that we have specified:

- A network

- Loss function

How do we find the values for the weights that gives us the smallest possible value for the loss function?

How do we minimize the loss function?

Gradient Decscent

Give weights random initial values
Evaluate partial derivative of each weight with respect negative log-likelihood at current weight value
Take a step in direction opposite to the gradient
Rinse and repeat

THE OPTIMIZER

How do we minimize the loss function?

THE OPTIMIZER

Many variations on basic idea of SGD are available

MODERN NEURAL NETS

MODERN DEEP LEARNING

Several key advancements have enabled the modern deep learning revolution

Advent of massively parallel computing by GPUs. Enabled training of huge neural nets on extremely large datasets

MODERN DEEP LEARNING

Several key advancements have enabled the modern deep learning revolution

Advent of massively parallel computing by GPUs. Enabled training of huge neural nets on extremely large datasets

Several key advancements have enabled the modern deep learning revolution

Methodological advancements have made deeper networks easier to train

Architecture

Optimizers

Activation Functions

MODERN DEEP LEARNING

Several key advancements have enabled the modern deep learning revolution

MODERN DEEP LEARNING

Regularization is key!

Dropout

L1 & L2

Several key advancements have enabled the modern deep learning revolution

MODERN DEEP LEARNING

Transfer Learning

Train big model

on large dataset

Refine model

on smaller dataset

Several key advancements have enabled the modern deep learning revolution

Robust frameworks and abstractions make iteration faster and less error prone

Automatic differentiation allows easy prototyping

MODERN DEEP LEARNING

KERAS & MLP EXERCISE

Exercise 1

https://github.com/beamandrew/HSPH_lecture

CONVOLUTIONAL NEURAL NETWORKS

CONVOLUTIONAL NEURAL NETS (CNNs)

Dates back to the late 1980s

Invented by in 1989 Yann Lecun at Bell Labs - "Lenet"
Integrated into handwriting recognition systems
in the 90s
Huge flurry of activity after the Alexnet paper

THE BREAKTHROUGH (2012)

Imagenet Database

Millions of labeled images
Objects in images fall into 1 of a possible 1,000 categories
Relatively high-resolution
Bounding boxes giving exact location of object - useful for both classification and localization

Large Scale Visual

Recognition Challenge (ILSVRC)

Annual Imagenet Challenge starting in 2010
Successor to smaller PASCAL VOC challenge
Many tracks including classification and localization
Standardized training and test set. Competitors upload predictions for test set and are automatically scored

THE BREAKTHROUGH (2012)

Pivotal event occurred in an image recognition contest which brought together 3 critical ingredients for the first time:

Massive amounts of labeled images
Training with GPUs
Methodological innovations that enabled training deeper networks while minimizing overfitting

THE BREAKTHROUGH (2012)

In 2011, a misclassification rate of 25% was near state of the art on ILSVRC

In 2012, Geoff Hinton and two graduate students, Alex Krizhevsky and Ilya Sutskever, entered ILSVRC with one of the first deep neural networks trained on GPUs, now known as "Alexnet"

Result: An error rate of 16%, nearly half what the second place entry was able to achieve.

The computer vision world immediately took notice

THE ILSVRC AFTERMATH (2012-2014)

Alexnet paper has ~ 16,000 citations since being published in 2012!

Most algorithms expect "tabular" data

WHY CNNS WORK

y	X1	X2	X3	X4
0	7	52	17	654
0	23	2752	4	1
1	786	27	0	5
0	354	7527	89	68

The problem with tabular data

What is this a picture of?

WHY CNNS WORK

What is this a picture of?

The problem with tabular data

WHY CNNS WORK

What is this a picture of?

Tabular data throws away too much information!

The problem with tabular data

WHY CNNS WORK

CONVOLUTIONAL NEURAL NETS

Images are just 2D arrays of numbers

Goal is to build f(image) = 1

CONVOLUTIONAL NEURAL NETS

CNNs look at small connected groups of pixels using "filters"

Image credit: http://deeplearning.stanford.edu/wiki/index.php/Feature_extraction_using_convolution

Images have a local correlation structure

Near by pixels are likely to be more similar than pixels that are far away

CNNs exploit this through convolutions of small image patches

CONVOLUTIONAL NEURAL NETS

Example convolution

CONVOLUTIONAL NEURAL NETS

Pooling provides spatial invariance

Image credit: http://cs231n.github.io/convolutional-networks/

CONVOLUTIONAL NEURAL NETS

Convolution + pooling + activation = CNN

Image credit: http://cs231n.github.io/convolutional-networks/

CONVOLUTIONAL NEURAL NETS (CNNs)

CNN formula is relatively simple

Image credit: http://cs231n.github.io/convolutional-networks/

CONVOLUTIONAL NEURAL NETS

Data augmentation mimics the image generative process

Image credit: http://slideplayer.com/slide/8370683/

Drastically "expands" training set size
Improves generalization
Works if it doesn't "break" image -> label relationship

WHY DO CNNs WORK SO WELL?

Based on solid image priors
Exploit properties of images, e.g. local correlations and invariances
Mimic generative distribution with augmentation to reduce over fitting
Results in end-to-end visual recognition system trained with SGD on GPUs: pixels in -> classifications out

CNNs exploit strong prior information about images

WHY DOES DEEP LEARNING WORK?

https://simplystatistics.org/2017/05/31/deeplearning-vs-leekasso/

WHY DOES DEEP LEARNING WORK?

https://simplystatistics.org/2017/05/31/deeplearning-vs-leekasso/

WHY DOES DEEP LEARNING WORK?

http://beamandrew.github.io/deeplearning/2017/06/04/deep_learning_works.html

WHY DOES DEEP LEARNING WORK?

http://beamandrew.github.io/deeplearning/2017/06/04/deep_learning_works.html

CNN EXERCISE

Exercise 2

https://github.com/beamandrew/HSPH_lecture

SUMMARY & CONCLUSIONS

DEEP LEARNING AND YOU

Barrier to entry for deep learning is actually low

... but a few things might stand in your way:

Need to make sure your problem is a good fit
- Lots of labeled data and appropriate signal/noise ratio
Access to GPUs
Must "speak the language"
- Many design choices and hyper parameter selections
Know how to "babysit" the model during learning phase

CONCLUSIONS

Could potentially impact many fields -> understand concepts so you have deep learning "insurance"
Prereqs: Data (lots) + GPUs (more = better)
Easy incorporate problem structure directly into model
Deep learning models are like legos, but you need to know what blocks you have and how they fit together
Need to have a sense of sensible default parameter values to get started
"Babysitting" the learning process is a skill

SEE YOU IN THE SPRING!

HSPH Lecture

By beamandrew

HSPH Lecture

1,836