Health Data Science Meetup
October 10, 2016
Regularization
Git and GitHub
Implementations in Python
Regularization
Linear Regression with One Variable
The hypothesis function:
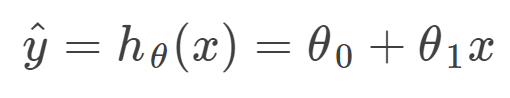
Cost function:
- measures the accuracy of our hypothesis function by using a cost function.
- takes an average of all the results of the hypothesis with inputs from x's compared to the actual output y's
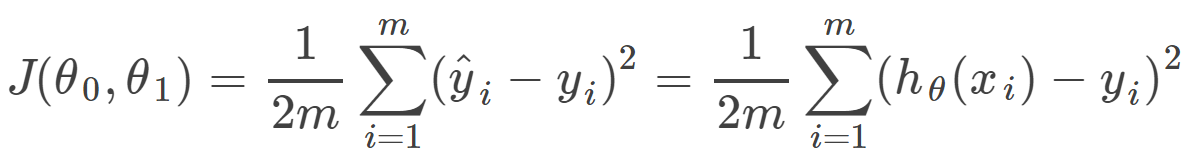
- This function is otherwise called the "Squared error function", or "Mean squared error".
- The mean is halved as a convenience for the computation of the gradient descent, as the derivative term of the square function will cancel out the 1/2 term.
Gradient Descent
Now we need to estimate the parameters in hypothesis function.

- The way we do this is by taking the derivative of our cost function.
- The slope of the tangent is the derivative at that point and it will give us a direction to move towards.
- We make steps down the cost function in the direction with the steepest descent, and the size of each step is determined by the parameter α, which is called the learning rate.
Gradient Descent
The gradient descent algorithm is:
repeat until convergence:
where j=0,1 represents the feature index number.

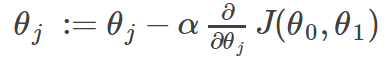
Gradient Descent for Linear Regression:
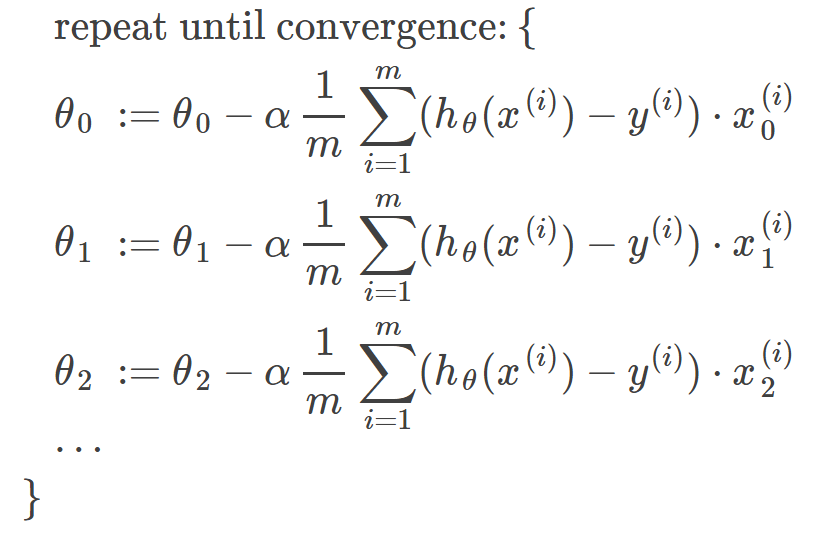
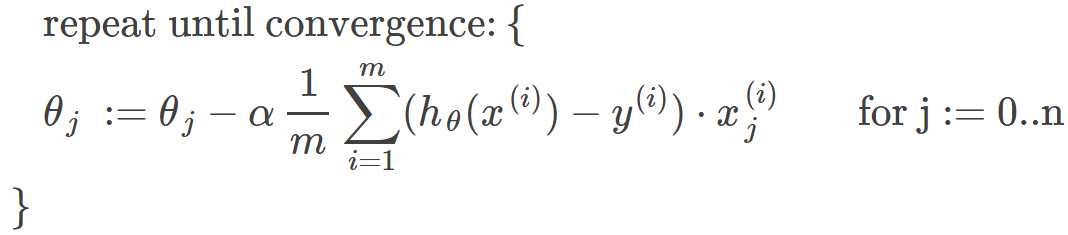
Why Gradient Descent?
Normal Equation:
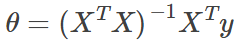
| Gradient Descent | Normal Equation |
|---|---|
| Need to choose alpha | No need to choose alpha |
| Needs many iterations | No need to iterate |
| Works well when n is large |
Slow if n is very large |
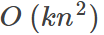
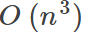
For large datasets, we usually use stochastic gradient descent.
Regularization
-
High bias or underfitting:
- when the form of our hypothesis function h maps poorly to the trend of the data.
- It is usually caused by a function that is too simple or uses too few features. -
High variance or overfitting:
- caused by a hypothesis function that fits the available data but does not generalize well to predict new data.
- It is usually caused by a complicated function that creates a lot of unnecessary curves and angles unrelated to the data. -
Two main options to address overfitting:
- Reduce the number of features (manually select which features to keep/use a model selection algorithm)
- Regularization (Keep all the features, but reduce the parameters θ)
Regularization
If we have overfitting from our hypothesis function, we can reduce the weight that some of the terms in our function carry by increasing their cost.
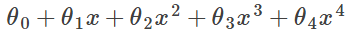
We want to make it more quadratic
We'll want to eliminate the influence of the cubic and quartic terms.
Without actually getting rid of these features or changing the form of our hypothesis, we can instead modify our cost function:
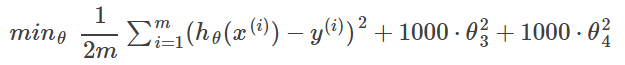
In general:
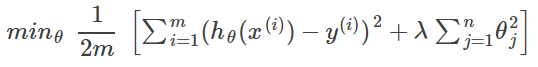
L2 regularization (Ridge)
Regularization
L1 regularization (Lasso):
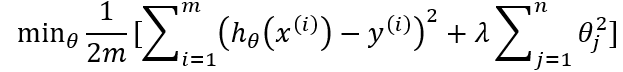
L2 regularization (Ridge):
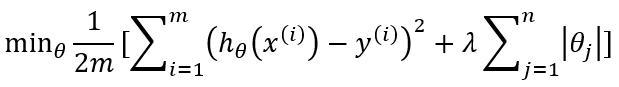
L1+L2 regularizations (Elastic net):
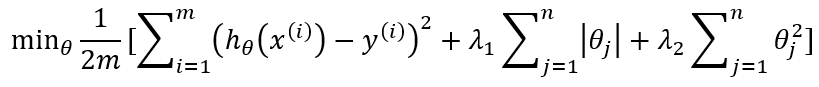
Comparisons
- L1 regularization helps perform feature selection in sparse feature spaces
- L1 rarely perform better than L2
- when two predictors are highly correlated, L1 regularizer will simply pick one of the two predictors
- in contrast, the L2 regularizer will keep both of them and jointly shrink the corresponding coefficients a little bit
- Elastic net has proved to be (in theory and in practice) better than L1/Lasso
Git and GitHub
What?
- Git: software which keeps track of code changes
- GitHub: a popular server for storing repositories
Why?
- Keeps a full history of changes
- Allows multiple programmers to work on the same codebase
- Is efficient and lightweight (records file changes, not file contents)
- Public repositories on GitHub can serve as a coding resume.
Install Git
Create a GitHub Account
Create a Pair of SSH Keys
- SSH keys are one way of securely communicating with GitHub.
- Step-by-step directions at: https://help.github.com/articles/generating-ssh-keys






Basic Git Configuration
git config --global user.name "User Name"
git config --global user.email "user@email.com"
Pull the Codes
git clone https://github.com/benhhu/HDSMeetup.git
Python
HDS Meetup 10/10/2016
By Hui Hu
HDS Meetup 10/10/2016
Slides for the Health Data Science Meetup
- 960



