Health Data Science Meetup
November 7, 2016
Support Vector Machines
Implementations in Python
Support Vector Machines
Introduction
- Introduced in the 1992 Conference in Learning Theory by Boser, Guyon & Vapnik
- Successful applications in many fields: bioinformatics, text, image recognition, etc.
- Textbook:
An Introduction to Support Vector Machines. Cristianini & Shawe-Taylor

Binary Classification

Logistic Regression
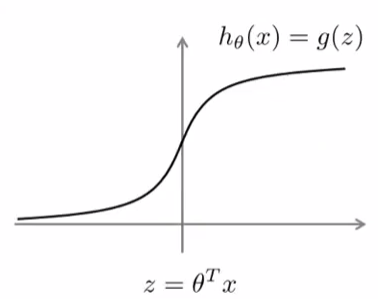
Sigmoid Function / Logistic Function

Decision Boundary

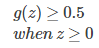

Cost Function
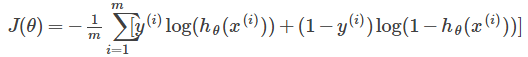
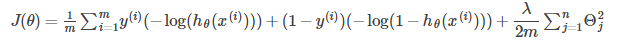
Alternative View of Logistic Regression
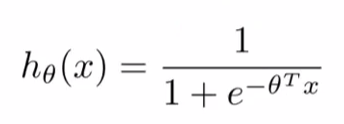
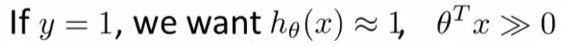
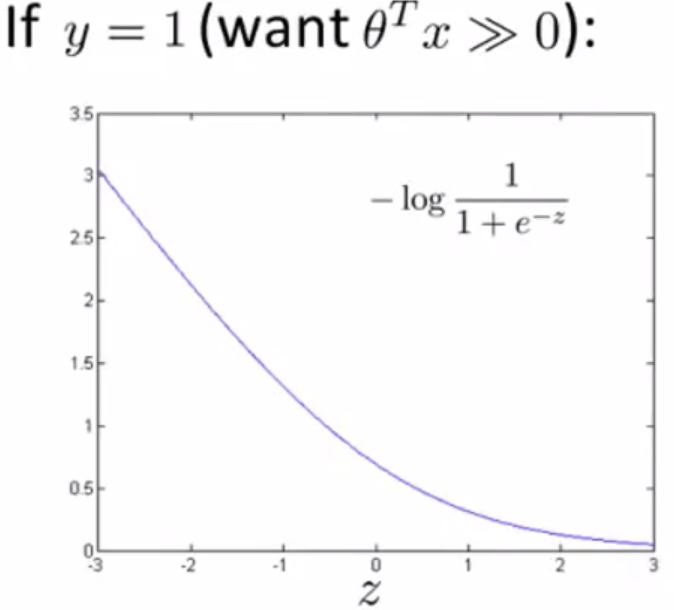
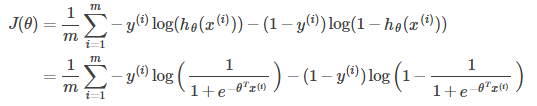
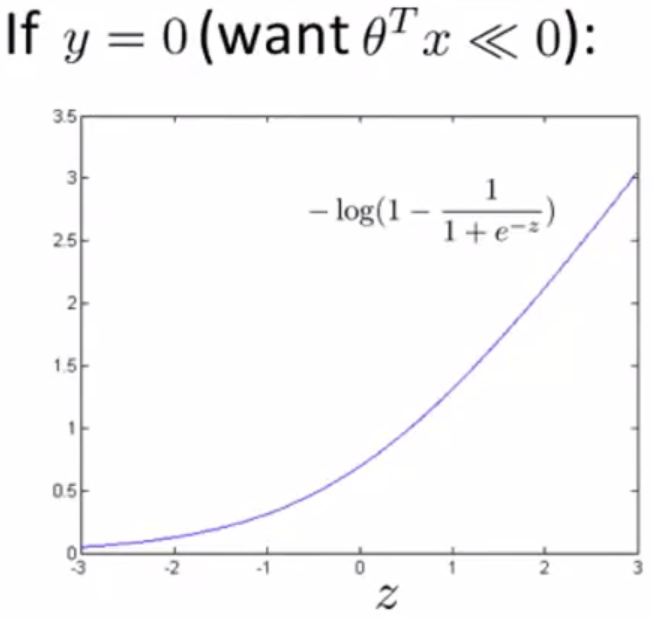
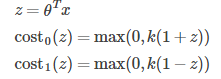
Cost Function
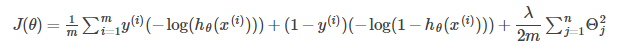
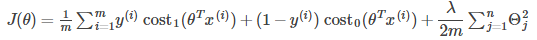
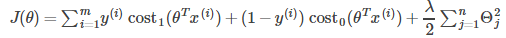
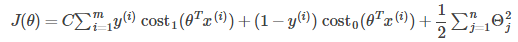
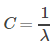
Large Margin Classifiers

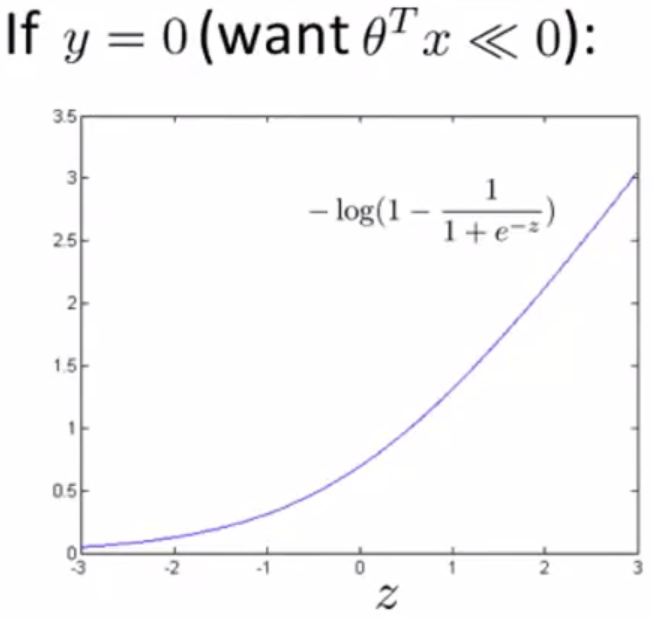
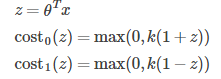

If we set C to a very large value, the optimization of cost function will focus on the left part of the cost function.
Choose parameters such that:
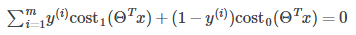

Large Margin Classifier
x_1
x1
x_2
x2
Soft Margin Classifier
x_1
x1
x_2
x2
Very large C
C not too large
Non-linear Decision Boundary
x_1
x1
x_2
x2
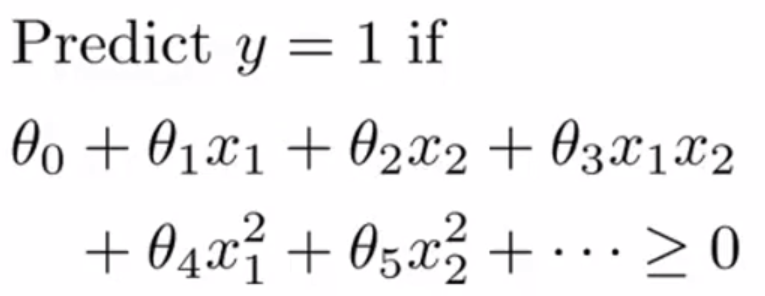
\theta_0+\theta_1f_1+\theta_2f_2+...
θ0+θ1f1+θ2f2+...
We can use different functions
Kernel
x_1
x1
x_2
x2
l^{(1)}
l(1)
l^{(2)}
l(2)
l^{(3)}
l(3)
- Given x, compute new feature depending on proximity to landmarks
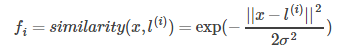
Gaussian Kernels
x
x
f_1\approx1, f_2\approx0, f_3\approx0
f1≈1,f2≈0,f3≈0
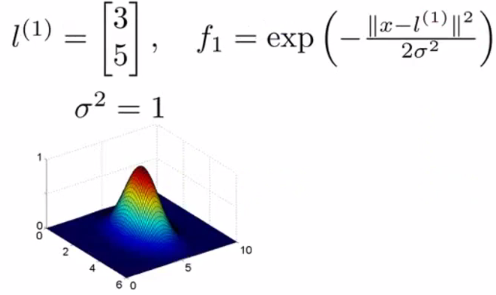
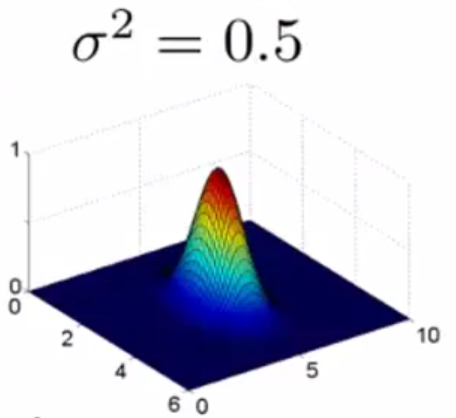
x_1
x1
x_2
x2
f_1
f1

Kernel
Where to get ?
l^{(1)},l^{(2)},l^{(3)}
l(1),l(2),l(3)
x_1
x1
x_2
x2
x_1
x1
x_2
x2
l^{(1)}
l(1)
x^{(1)}
x(1)
SVM Parameters
- Large C: Lower bias, high variance
- Small C: Higher bias, low variance
C=1/\lambda
C=1/λ
\sigma^2
σ2
for Gaussian Kernel
- Large : Higher bias, low variance
Features vary more smoothly. - Small : Lower bias, high variance
Features vary less smoothly
\sigma^2
σ2
\sigma^2
σ2
f_i
fi
f_i
fi
Kernel
- Linear Kernel SVM
- Polynomial Kernel SVM
- Gaussian (Radial basis function or rbf) Kernel SVM
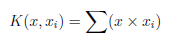
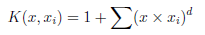
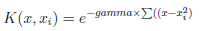
Python
HDS Meetup 11/7/2016
By Hui Hu
HDS Meetup 11/7/2016
Slides for the Health Data Science Meetup
- 986



