Geographically Weighted Regression

Traditional Regression Models

• If we apply a traditional regression model to spatial data, we usually assume a stationary process
  -  the same exposure has the same impact on the outcome in all parts of the study region
  
  
   
• The estimated coefficients are constant over space
  -  assume that the values of β are the same everywhere

Measured Associations Might Vary Spatially

• Sampling variation
   
• Associations intrinsically different across space
  -  e.g. differences in attitudes, different political or other contextual effects
   
• Model misspecification

Geographically Weighted Regression

• To address the issue of spatial non-stationary directly and allow the associations to vary over space
  
  
  
   
• We can then estimate the values of β by:
  
  
   
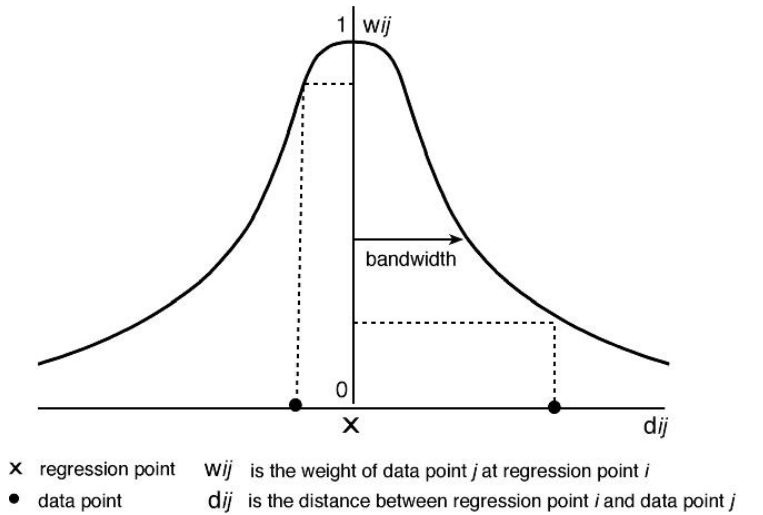
• W(i) is a weight matrix specific to location i such that observations nearer to i are given greater weight than observations further away

A Typical Spatial Weight Function

Spatial Weight Functions

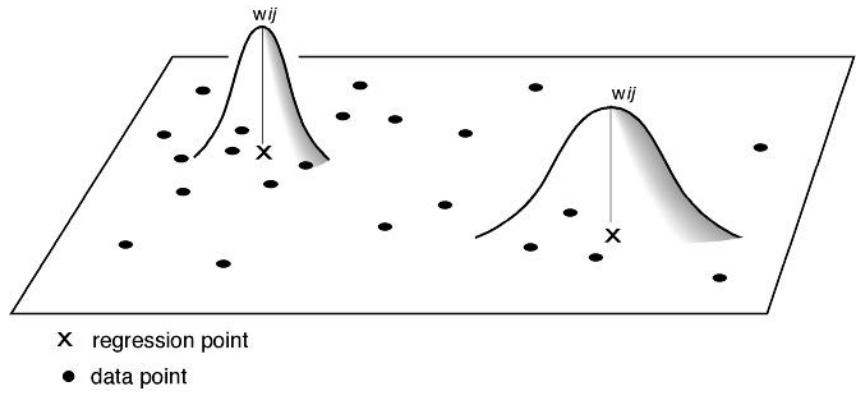
• Numerous weight functions can be used
  -  usually use Gaussian or "Gaussian-like" functions to reflect the type of dependency found in most spatial processes
  -  can be either fixed or adaptive

Fixed

Adaptive

h is the bandwidth, as it increases, the gradient of the kernel becomes less steep and more data points are incuded

if j is one of the Nth nearest neighbors of i

otherwise

Calibration

• Results of GWR appear to be relatively insensitive to the choice of weighting functions
  -  as long as it is a continuous distance-based function
   
• However, the results will be sensitive to the degree of distance-decay
   
• Therefore, an optimal value of either h or N has to be obtained
  -  through minimizing a cross-validated score or the AIC

Bandwidth Selection

• Optimal bandwidth selection is a trade-off between bias and variance
  -  too small a bandwidth leads to large variance in the local estimates
  -  too large a bandwidth leads to large bias in the local estimates

Output from GWR

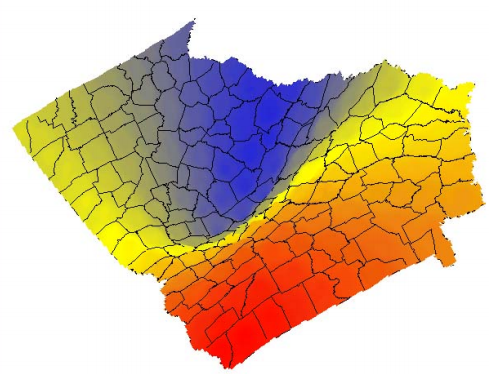
• Main output from GWR is a set of location-specific coefficient estimates which can be mapped and analyzed to provide information on spatial non-stationary in associations
   
• We  can also use GWR to
  -  estimate local standard errors
  -  derive local t statistics
  -  calculate local goodness-of-fit measures
  -  perform tests to assess the significance of the spatial variation in the local parameter estimates
  -  perform tests to determine if the local model performs better than the global one

Lab: GWR

git pull