Congruent Triangles Theorems and Postulates
By: Benjamin Liberles
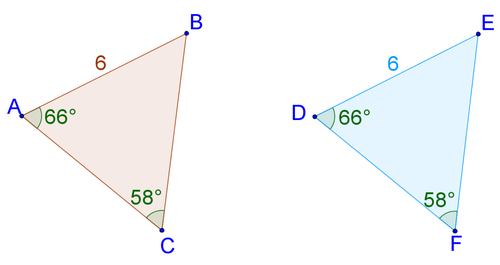
Side-Side-Side (SSS)
When a triangle has 3 congruent sides to another triangle.
Ex.
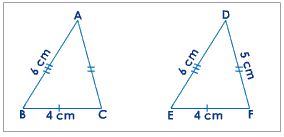
Triangle ABC is congruent to triangle DEF. Each line segment is congruent to the line segment of the other triangle with the same amount of tick marks. Line segment AB is congruent to line segment DE both being 6 cm, BC to EF being 4 cm each, and CA to FD both being 5 cm.
Side-Side-Side (SSS) Postulate
If three sides of one ∆ are ≅ to three sides of a second ∆, then the two ∆s are ≅.
Triangle ABC is congruent to triangle DEF.
Side-Angle-Side (SAS)
When two triangles have two congruent sides and one congruent angle between the two congruent sides.
Ex.
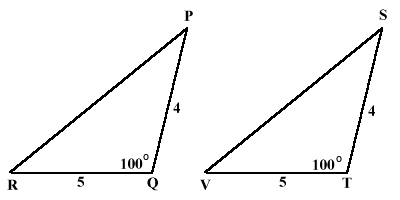
Triangle PQR is congruent to triangle STV. Sides PQ and ST are congruent and sides QR and TV are congruent, angle PQR
and angle STV are congruent.
Side-Angle-Side (SAS) Postulate
If two sides and the included ∡ of one ∆ are ≅ to two sides and the included ∡ of another ∆, then the two ∆s are ≅.
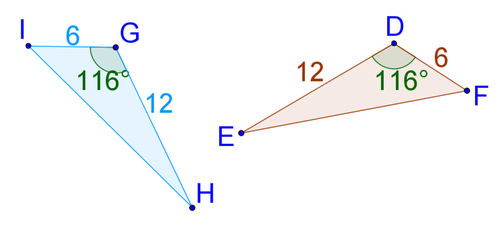
Triangle GHI is congruent to triangle DEF.
Angle-Side-Angle
(ASA)
When two triangles have two congruent angles and one congruent side between the two congruent angles.
Ex.
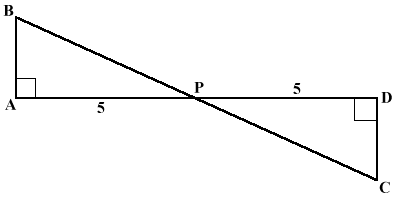
Triangle ABP is congruent to triangle DCP. Angle BAP and angle CDP are congruent, angles BPA and CPD are vertical angles, which makes them congruent and side AP and DP are congruent.
Angle-Side-Angle
(ASA) Postulate
If two ∡s and the included side of one ∆ are ≅ to two ∡s and the included side of another ∆, then the two ∆s are ≅.
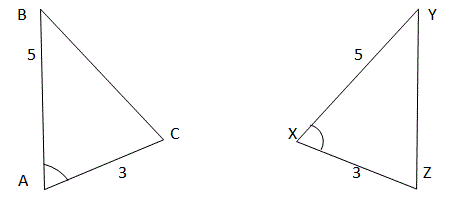
Triangle ABC is congruent to triangle XYZ.
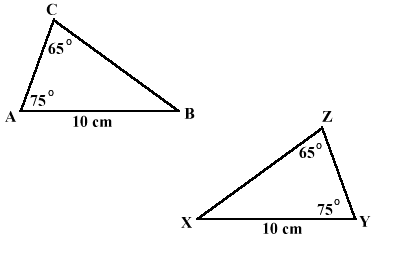
Angle-Angle-Side (AAS)
When two triangles have two congruent angles and one non-included congruent slide.
Ex.
Triangle ABC is congruent to triangle YXZ. Angles CAB and XYZ are congruent, angles ACB and XZY are congruent and side AB and YX are congruent.
Angle-Angle-Side (AAS) Postulate
If two ∡s and the non-included side of one ∆ are ≅ to two ∡s and the non-included side of another ∆, then the two ∆s are ≅.
Triangle ABC is congruent to triangle DEF.
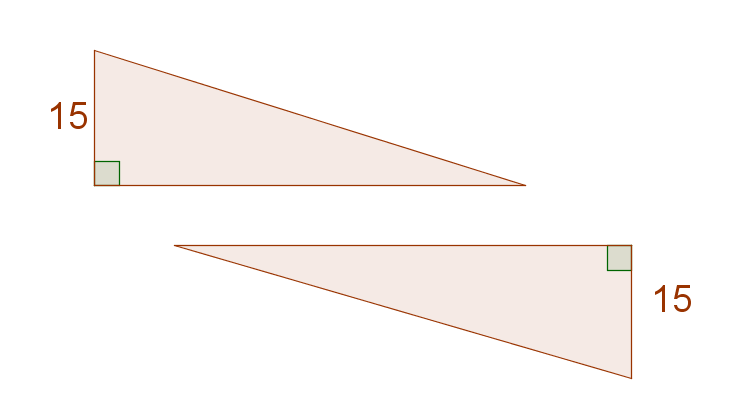
Hypotenuse Leg (HL)
When two right triangles' hypotenuses are congruent and one side from each triangle are congruent.
Ex.
Triangle ABC is congruent to triangle ZYX. Hypotenuses AC and ZX are congruent and sides AB and ZY are congruent.
A
B
C
X
Y
Z
= congruent tally mark
Hypotenuse Leg (HL)
Theorem
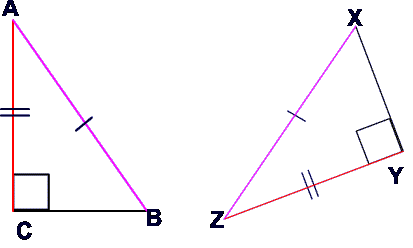
If the hypotenuse and a leg of ⊿ are ≅ to a hypotenuse and a leg of a second ⊿, then the two ∆s are ≅.
Triangle ABC is congruent to triangle XZY.
28
28
Congruent Triangles Theorems and Postulates By: Benjamin Liberles
Congruent Triangles Project
By benjaminliberles
Congruent Triangles Project
- 7,511