k-means, LASSO, and Random Forest

Applications for Machine Learning Working Group from

 

The Mortality and Medical Costs of Air Pollution: Evidence from Changes in Wind Direction

paper Summary

  • Measure the impact of fine particulate matter pollution (PM 2.5) on mortality and healthcare use
  • IV approach that leverages local wind changes on (non-local) pollution
  • Use machine learning to simulate life-years lost (LYL) due to pollution exposure
    • K-means for data cleaning
    • Hazard rate refinement using high-dimensional datasets
      • LASSO
      • Random Forest
    • Chernozhukov et al. (2018) ML for heterogeneity (I won't cover, highly technical that would probably need its own session)

Empirical strategy

  • How to estimate how long someone has to live?
  • Cox proportional hazards model

Empirical strategy

  • How to estimate how long someone has to live?
  • Cox proportional hazards model:
h(t_i|x_i,\beta)=\underbrace{h_0(t_i)}\underbrace{exp[x_i'\beta]}

Baseline survival rate

Individual characteristics

Empirical strategy

  • How to estimate how long someone has to live?
  • Cox proportional hazards model:
h(t_i|x_i,\beta)=\underbrace{h_0(t_i)}\underbrace{exp[x_i'\beta]}

Baseline survival rate

Individual characteristics

>1: increased risk

<1: decreased risk

Empirical strategy

  • How to estimate how long someone has to live?
  • Cox proportional hazards model:
h(t_i|x_i,\beta)=\underbrace{h_0(t_i)}\underbrace{exp[x_i'\beta]}

Baseline survival rate

Individual characteristics

Estimate with log partial likelihood

Empirical strategy

  • How to estimate how long someone has to live?
  • Cox proportional hazards model:
h(t_i|x_i,\beta)=\underbrace{h_0(t_i)}\underbrace{exp[x_i'\beta]}

Estimate with log partial likelihood

\ln L(\beta) = \sum^N_{i=1} \delta_i \left[ x_i'\beta - \ln \sum_{j \in R(t_i)} \exp[x_j'\beta] \right]

Empirical strategy

  • How to estimate how long someone has to live?
  • Cox proportional hazards model:
h(t_i|x_i,\beta)=\underbrace{h_0(t_i)}\underbrace{exp[x_i'\beta]}
\ln L(\beta) = \sum^N_{i=1} \delta_i \left[ x_i'\beta - \ln \sum_{j \in R(t_i)} \exp[x_j'\beta] \right]

Observe death =1

The risk set: the entire set of subjects at risk at time i

Characteristics of those individuals

Empirical strategy

  • How to estimate how long someone has to live?
  • Cox proportional hazards model:
h(t_i|x_i,\beta)=\underbrace{h_0(t_i)}\underbrace{exp[x_i'\beta]}
\ln L(\beta) = \sum^N_{i=1} \delta_i \left[ x_i'\beta - \ln \sum_{j \in R(t_i)} \exp[x_j'\beta] \right]

Maximize this, or rather, minimize the negative of this

Intuitively, choose β such that it weights riskier characteristics more

Sources: https://en.wikipedia.org/wiki/Proportional_hazards_model and http://www.sthda.com/english/wiki/cox-proportional-hazards-model

Problem:

  • There are nearly 1,400 PM 2.5 monitors in the country, but they are sparsely placed.
  • Locally produced pollution will generate data noise based on proximity to certain monitors.
  • Local pollution unlikely to reach all individuals in a given area.

Measurement Error!

Problem:

  • There are nearly 1,400 PM 2.5 monitors in the country, but they are sparsely placed.
  • Locally produced pollution will generate data noise based on proximity to certain monitors.
  • Local pollution unlikely to reach all individuals in a given area.

Measurement Error!

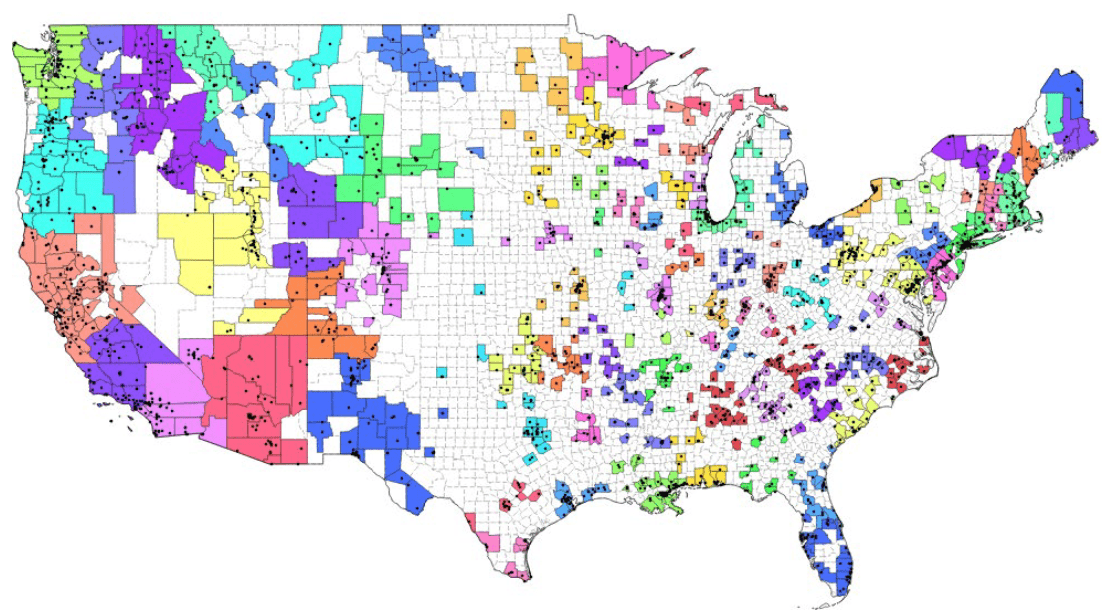
Focus on systematic pollution by grouping together monitors in multiple counties

Problem:

  • There are nearly 1,400 PM 2.5 monitors in the country, but they are sparsely placed.
  • Locally produced pollution will generate data noise based on proximity to certain monitors.
  • Local pollution unlikely to reach all individuals in a given area.
  • Unsupervised machine learning technique
  • Partitions data around associated centroids, based on the number of clusters k chosen in advance
  • Simple method (the "OLS of clustering") of classifying geospatial or even data that might not have interpretable distance (e.g. Spotify songs)

 

k-means clustering

If we want to be more sophisticated than just picking the monitor groups ourselves...

The algorithm

  • (Possibly, especially if not geospatial)
    scale and normalize features
  • Select K points for initial centroids
  • Begin while loop
    • Form K clusters by assigning all
      points to the closest centroid
    • Recompute the centroid for each
      cluster
  • Stop loop when centroids are stable (usually fairly rapidly but complexity increases in data points, clusters K, and features)

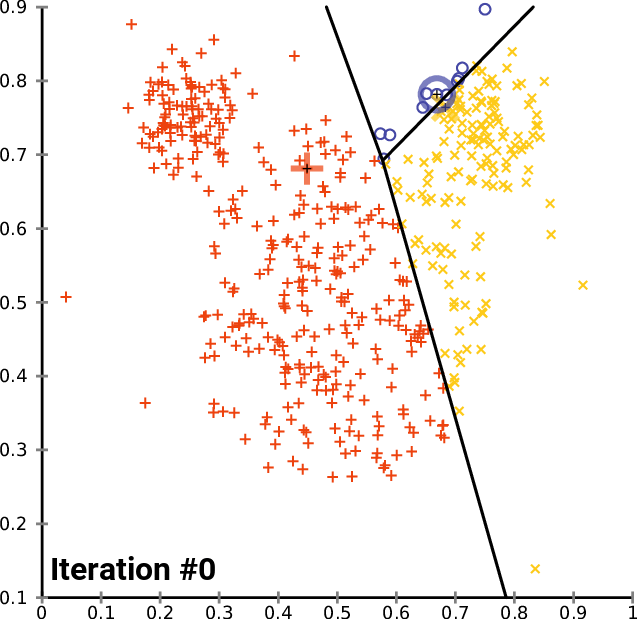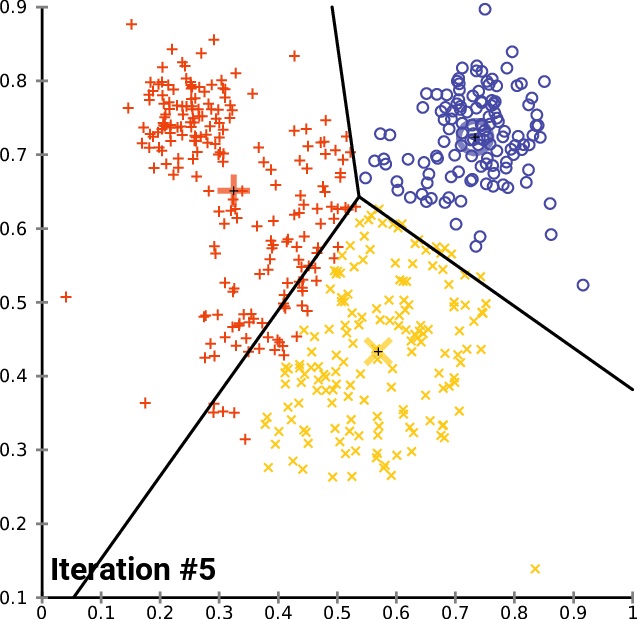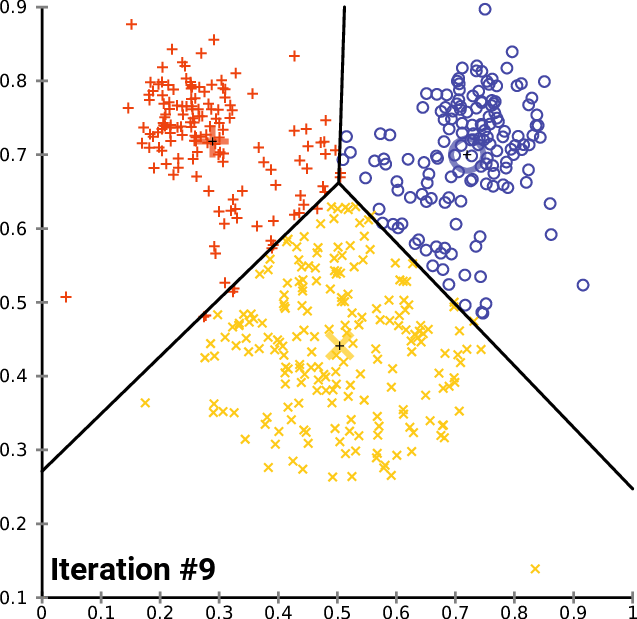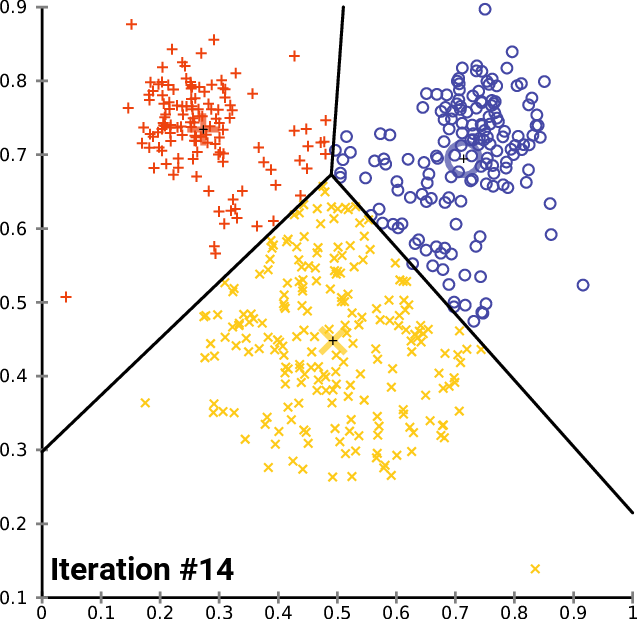
Source: https://github.com/jgscott/ECO395M

The algorithm

  • (Possibly, especially if not geospatial)
    scale and normalize features
  • Select K points for initial centroids
  • Begin while loop
    • Form K clusters by assigning all
      points to the closest centroid
    • Recompute the centroid for each
      cluster
  • Stop loop when centroids are stable (usually fairly rapidly but complexity increases in data points, clusters K, and features)
  • Might need to spot-check clusters, if possible
  • Each iteration will be different
    • Set seed, or
    • Use 20+ starts (many packages will choose the start with the lowest within-cluster variation), or
  • Use a different initialization strategy K-means++

Some Issues

Choose initial
centroid

K-means++

Choose initial
centroid

Compute distance to x's

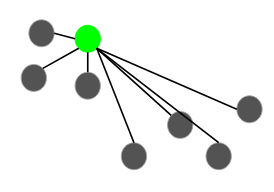
K-means++

Choose initial
centroid

Compute distance to x's

Probabilistically weight furthest as next centroid

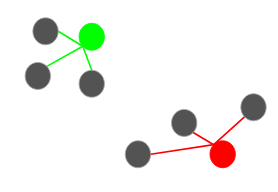
K-means++

Choose initial
centroid

Compute distance to x's

Probabilistically weight furthest as next centroid

Stop when you reach K centroids

K-means++

Source: https://www.analyticsvidhya.com/blog/2019/08/comprehensive-guide-k-means-clustering/

Toy Example

Problem:

  • How do we know what is important for how long someone will live?
  • We could use some economic intuition to guess, but this is subjective

Problem:

  • How do we know what is important for how long someone will live?
  • We could use some economic intuition to guess, but this is subjective
  • Huge dataset with more than 1000 variables, so simply testing one against another is infeasible

Problem:

  • How do we know what is important for how long someone will live?
  • We could use some economic intuition to guess, but this is subjective
  • Huge dataset with more than 1000 variables, so simply testing one against another is infeasible

Reduce Dimensions

Problem:

  • How do we know what is important for how long someone will live?
  • We could use some economic intuition to guess, but this is subjective
  • Huge dataset with more than 1000 variables, so simply testing one against another is infeasible

Reduce Dimensions

Machine Learning can train on data to select important variables

Problem:

  • How do we know what is important for how long someone will live?
  • We could use some economic intuition to guess, but this is subjective
  • Huge dataset with more than 1000 variables, so simply testing one against another is infeasible
  • Least absolute shrinkage and selection operator
  • Makes explicit the tradeoff between choosing covariates to minimize the differences between predicted y and observed y (goodness of fit) and selecting on too many variables (overfitting)
  • Can be applied easily to linear regression, proportional hazard, and many other empirical strategies, when it is not clear what is important

 

LASSO

Solution 1:

LAsso

  • LASSO takes the generic form

 

 

 

where dev is closeness of fit and pen is a penalty function on any beta that is non-zero.

  • In linear regression using L1 regularization as the penalty, we get a Lagrangian optimization problem that takes the form

 

 

 

 

 

\min_{\beta \in \R^p} \frac{1}{n} \text{dev} +\lambda \text{pen}(\beta)
\min_{\beta \in \R^p} \left( \frac{1}{n} (y-X\beta)^2 +\lambda \sum_\beta|\beta| \right)
\min_{\beta \in \R^p} \frac{1}{n} \text{dev} +\lambda \text{pen}(\beta)
\min_{\beta \in \R^p} \left( \frac{1}{n} (y-X\beta)^2 +\lambda \sum_\beta|\beta| \right)

How is this Machine Learning?

\min_{\beta \in \R^p} \frac{1}{n} \text{dev} +\lambda \text{pen}(\beta)
\min_{\beta \in \R^p} \left( \frac{1}{n} (y-X\beta)^2 +\lambda \sum_\beta|\beta| \right)

How is this Machine Learning?

  • Chosen value of lambda is data-dependent
  • Apply validation tools (e.g. cross-validation to determine optimal value)
\min_{\beta \in \R^p} \left( \frac{1}{n} (y-X\beta)^2 +\lambda \sum_\beta|\beta| \right)

How is this Machine Learning?

  • Chosen value of lambda is data-dependent
  • Apply validation tools (e.g. cross-validation to determine optimal value)

algorithm

  • Start with \( \lambda_1 \) so big that any \( \hat{\beta} =0  \)
  • For each iteration update \( \hat{\beta} \) to be optimal under \( \lambda_t < \lambda_{t-1} \)
  • Use a testing set to pick the best \( \lambda \)
    • Need a rule, such as minimum \( \lambda \) or 1se rule (pick the largest \( \lambda \) still within 1 standard error of minimum)

Source: https://github.com/jgscott/ECO395M

Toy Example

Results

  • Trees are sequential decision nodes that branch on inputs to predict the output

 

Random forest

Solution 2:

Source: https://github.com/jgscott/ECO395M

  • Trees are sequential decision nodes that branch on inputs to predict the output

 

Random forest

Source: https://github.com/jgscott/ECO395M

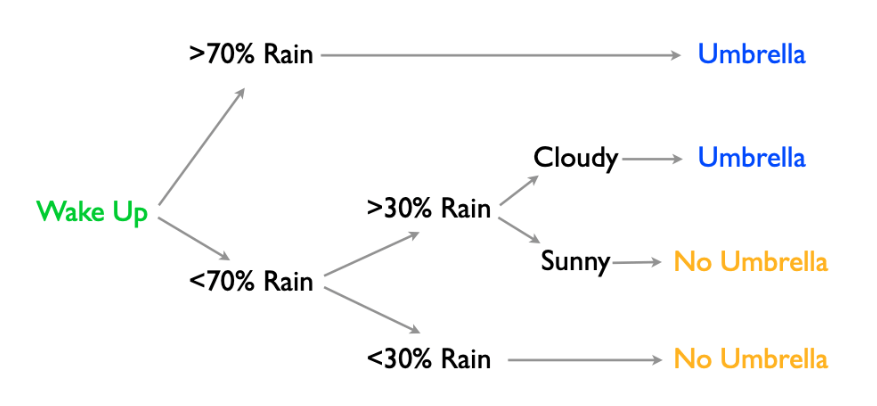
  • Trees are sequential decision nodes that branch on inputs to predict the output
  • Based on previous data, use to either
    • Categorize:  \( P(Y|X) \)
    • Estimate:  \( E(Y|X) \)
  • For numeric x, the decision rule is x<c

Random forest

Source: https://github.com/jgscott/ECO395M

  • Trees are sequential decision nodes that branch on inputs to predict the output
  • Based on previous data, use to either
    • Categorize:  \( P(Y|X) \)
    • Estimate:  \( E(Y|X) \)
  • For numeric x, the decision rule is x<c

Random forest

Source: https://github.com/jgscott/ECO395M

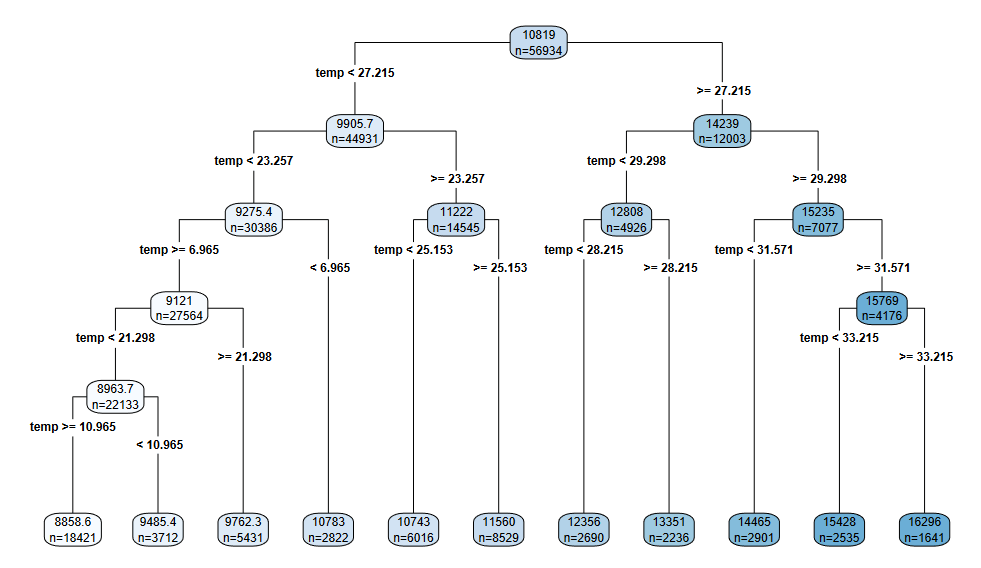
  • Trees are sequential decision nodes that branch on inputs to predict the output
  • Based on previous data, use to either
    • Categorize:  \( P(Y|X) \)
    • Estimate:  \( E(Y|X) \)
  • For numeric x, the decision rule is x<c
  • For categorical x, the rule says a set of categories goes left

Random forest

Source: https://github.com/jgscott/ECO395M

  • Trees are sequential decision nodes that branch on inputs to predict the output
  • Based on previous data, use to either
    • Categorize:  \( P(Y|X) \)
    • Estimate:  \( E(Y|X) \)
  • For numeric x, the decision rule is x<c
  • For categorical x, the rule says a set of categories goes left

Random forest

Source: https://github.com/jgscott/ECO395M

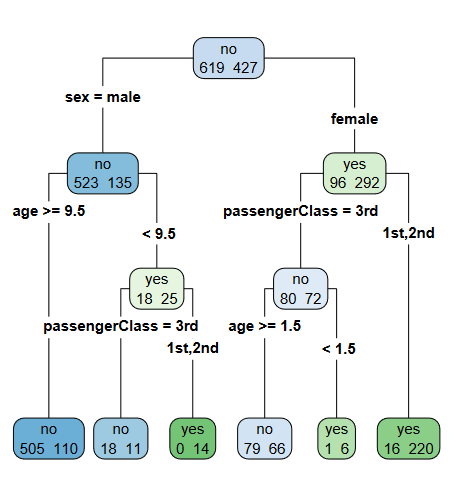
  • Trees are sequential decision nodes that branch on inputs to predict the output
  • Based on previous data, use to either
    • Categorize:  \( P(Y|X) \)
    • Estimate:  \( E(Y|X) \)
  • For numeric x, the decision rule is x<c
  • For categorical x, the rule says a set of categories goes left
  • The result is a partitioned space that makes choices on inputs and sends them down the tree

Random forest

Source: https://github.com/jgscott/ECO395M

Pruning Trees

  • Trees are always step functions

Pruning Trees

  • Trees are always step functions

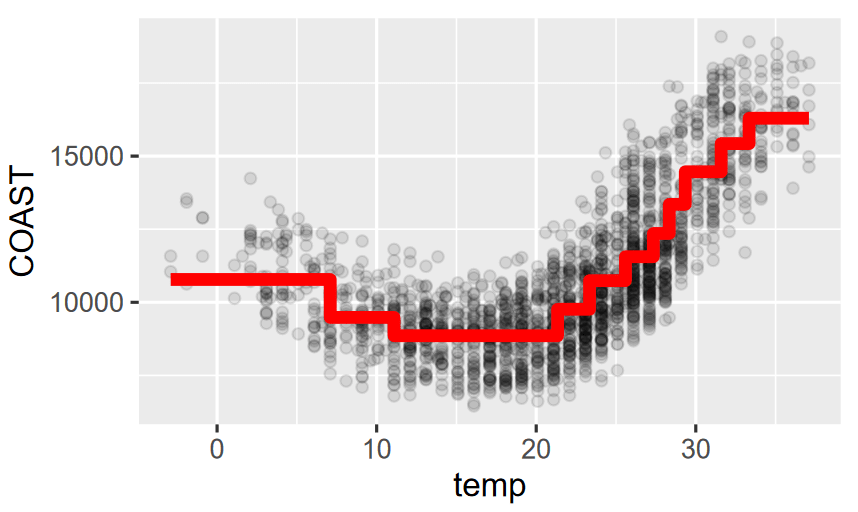
Pruning Trees

  • Trees are always step functions
  • They always consider interaction terms and nonlinearities (automatically because each node considers past nodes)
  • It also automatically ignore unimportant variables because they never increase fit
  • Pros: fast to fit, interpretable, and easily switch between numeric and categorical variables
  • Cons: don't scale well, each individual tree can be quite bad at predicting against the testing set
  • We'll need to prune!

Pruning Trees

  • Grow big:
    • Search over each possible splitting rule for the one that gives the biggest increase in fit
    • Stop once you reach a minimum threshold (e.g. we only have 10 observations per leaf)
    • This is probably overfitted!
  • Prune back
    • Search over all chosen splits for the one that is the least useful split for goodness of fit
    • Stop when you have only a single node
    • This has lost most explanatory power!
  • But these two processes give a sequence of trees that each of a bias-variance tradeoff that can be cross-validated

Seeing the Forest

  • Bootstrap aggregate ("bagging") over a huge collection of big and pruned trees to get a large selection of trees
  • Take the average of those trees and you get the forest

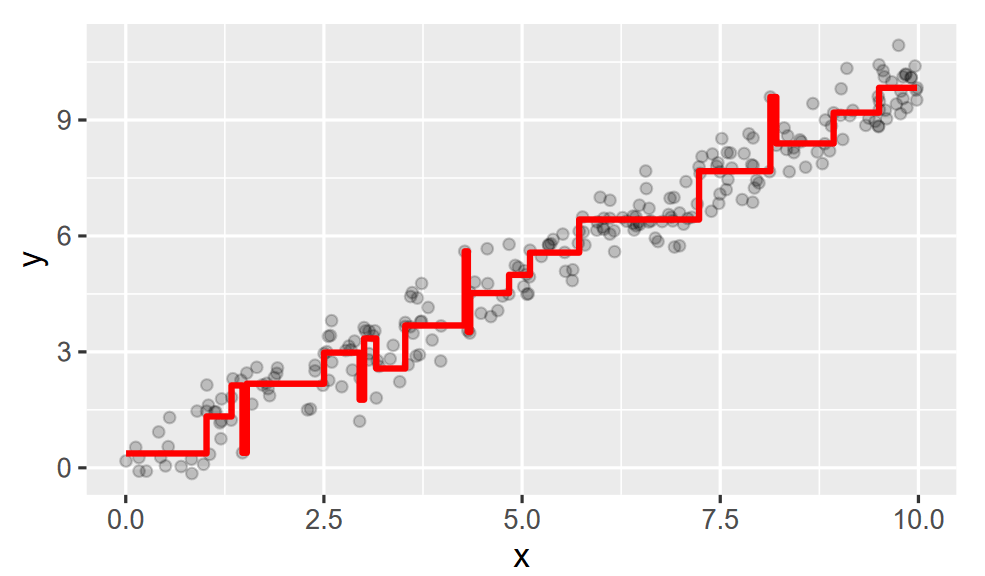
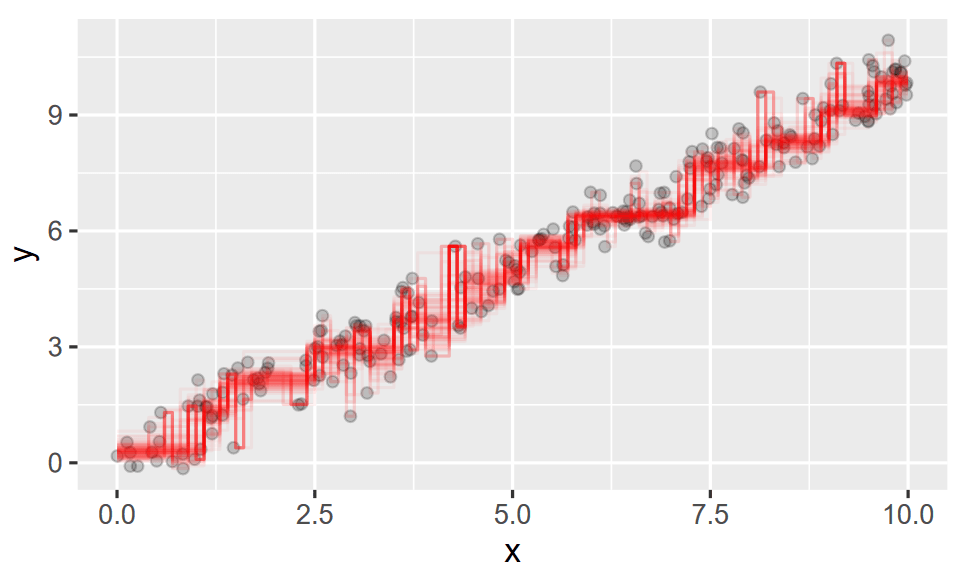
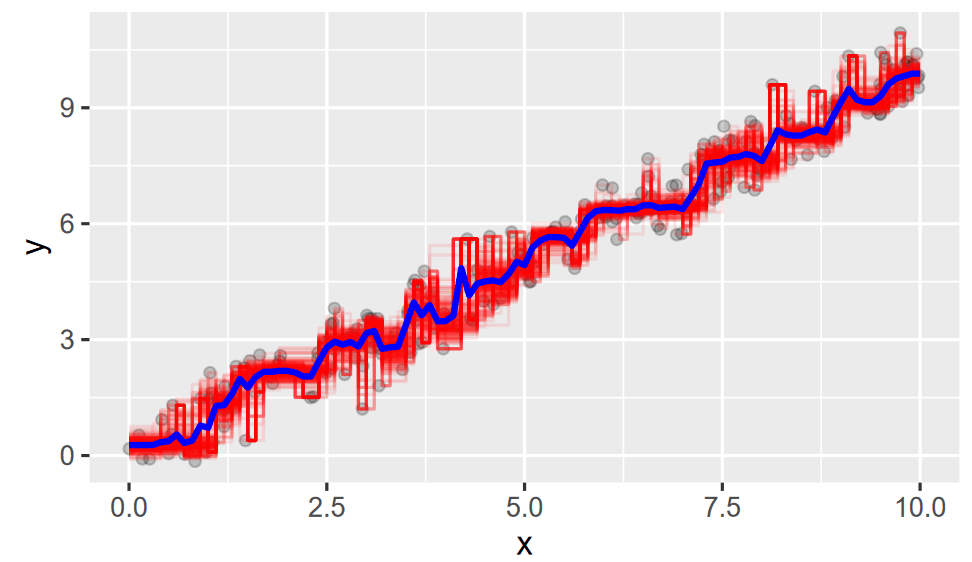
Seeing the Forest

  • Bootstrap aggregate ("bagging") over a huge collection of big and pruned trees to get a large selection of trees
  • Take the average of those trees and you get the forest

Seeing the Forest

  • Bootstrap aggregate ("bagging") over a huge collection of big and pruned trees to get a large selection of trees
  • Take the average of those trees and you get the forest

Seeing the Forest

  • Bootstrap aggregate ("bagging") over a huge collection of big and pruned trees to get a large selection of trees
  • Take the average of those trees and you get the forest

Toy Example

Results

Results

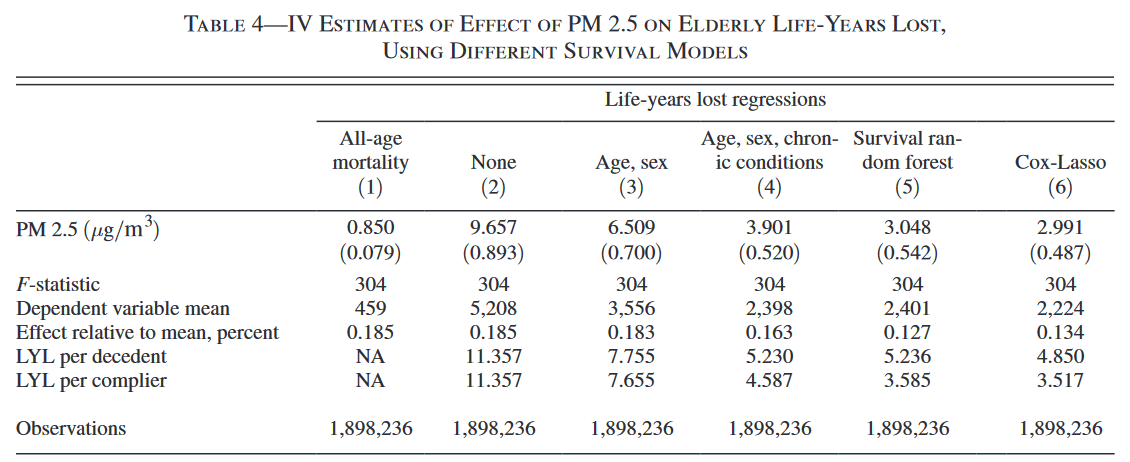
"The richness of our controls suggest this final estimate is about as good a representation of the true value as can be obtained empirically."

Results

"This drop indicates that mortality effects of PM 2.5 tend to be larger among individuals with characteristics that Cox-Lasso associates with lower life expectancy, even after conditioning on age, sex, and chronic conditions."

machine_learning_PM25

By bjw95

machine_learning_PM25

  • 61

More from bjw95