Objectives
- This is a time-constrained (22 minutes) presentation in anticipation of two upcoming conferences
- Most helpful:
- Feedback on presentation flow, pacing, and clarity (maybe best for the end?)
- Questions on content that would naturally emerge during a presentation
Veto Power, Delegation and Mechanism Design
Brandon Williams
Alistair Wilson
Richard Van Weelden
Student Practice Talk
September 25, 2025
Setup
Setup
- Many "bargaining" contexts exist in which a less-informed party must decide what to offer to a more-informed party, who hold veto power
Setup
- Many "bargaining" contexts exist in which a less-informed party must decide what to offer to a more-informed party, who hold veto power




Setup
- Many "bargaining" contexts exist in which a less-informed party must decide what to offer to a more-informed party, who hold veto power




Setup
- The proposers:
- Can make simple "take it or leave it" offers
- Or they can offer a range of options to the informed party, conceding some of their agenda-setting power
- The responders:
- Can accept the offer, or veto
- Or they can choose from the range, or veto
- Theory suggests that the delegation mechanism should capture any alignment friction and increase efficiency
- Behaviorally, this may not be the case
Theory
Theory
Kartik, Kleiner, Van Weelden (2021)
Theory
0
1
Theory

Proposer
0
1
Theory

Proposer
0
1
- Proposer has:
- Increasing payoff \( \pi (z) \) over the outcome \( z \) (for simplicity, we'll assume this is linear)
- Will make an offer to the vetoer
Theory


Vetoer
0
1
Proposer
\( \theta \)
- Veteor has:
- Ideal point \( \theta \) which is private information, \( \theta \sim F(\theta) \)
Theory


???
0
1
\( \theta \)
- Veteor has:
- Ideal point \( \theta \) which is private information, \( \theta \sim F(\theta) \)
Theory


???
0
1
- Veteor has:
- Ideal point \( \theta \) which is private information, \( \theta \sim F(\theta) \)
- A choice \( z \in \{0,Y\} \), either the veto threat point (here 0) or in the offer
\( \theta \)
Theory


- Veteor has:
- Ideal point \( \theta \) which is private information, \( \theta \sim F(\theta) \)
- A choice \( z \in \{0,Y\} \), either the veto threat point (here 0) or in the offer
0
1
Theory: Take it or Leave It


0
\( \theta \)
1
Theory: Take it or Leave It
0
1
Proposer
Offer \( y \)
\( \frac{ y}{2} \)
These \( \theta \)-types veto
These \( \theta \)-types choose offer
\( z = 0 \)
\( z = y \)
Theory: Take it or Leave It
0
1
Proposer
Offer \( y \)
\( \frac{ y}{2} \)
Suboptimal:
inefficient as \( \theta > y \)
preferred by both
Breakdown:
inefficient as \( \theta > 0 \)
Theory: Take it or Leave It
0
1
\( \frac{ y}{2} \)
\(f(\theta)\)
\( y \)
\( z = y \)
\( z = 0 \)
- Take it or leave it equilibrium depends on the distribution \( F(\theta) \)
- Increasing the offer \( y \) leads to:
- Marginal gain of \(\pi'(y)\cdot(1-F(\tfrac{y}{2}))\)
- Marginal loss of \(\left(\pi(y)-\pi(0)\right)\cdot \tfrac{1}{2}f(\tfrac{y}{2})\)
Theory: Delegation


0
\( \theta \)
1
Theory: Delegation
0
\( \theta \)
1
Vetoer
Proposer
- Proposer:
- Offers set of options \(Y\)
- Vetoer has:
- Chooses \(z\in\left\{0\right\}\cup Y\), either the veto threat point (here \(0\)) or some offer in delegation set
Theory: Delegation
0
1
\( \frac{ y}{2} \)
These \( \theta \)-types veto
These \( \theta \)-types
choose minimum offer
\( z = 0 \)
\( z = y \)
Offer \( [y,1] \)
\( y \)
These \( \theta \)-types
choose their preferred
\( z = \theta \)
Theory: Delegation
0
1
\( \frac{ y}{2} \)
Offer \( [y,1] \)
\( y \)
No suboptimality:
The delegation mechanism ensures
these options are available
Breakdown:
inefficient as \( \theta > 0 \)
Theory: Delegation
0
1
- Delegation equilibrium also depends on the distribution \( F(\theta) \)
- Increasing the minimum offer \( y \) leads to:
- Marginal gain of \(\pi'(y)\cdot(F(y)-F(\tfrac{y}{2}))\)
- Marginal loss of \(\left(\pi(y)-\pi(0)\right)\cdot \tfrac{1}{2}f(\tfrac{y}{2})\)
\(f(\theta)\)
\( \frac{ y}{2} \)
\( y \)
Theory: Delegation
- With increasing density we get a corner solution:
- Offer only the proposer maximum, \(y^\star=1\)
- With decreasing density we get the other corner solution:
- Full delegation, with \(Y^\star=\Theta\) and \(z^\star=\theta\)
Offer \( [y=1,1] \)
Offer \( [y=0,1] \)
0
1
\(f(\theta)\)
0
1
\(f(\theta)\)
Theory: Summary
- Delegation should capture a meaningful proportion of alignment failures, and therefore have more efficient outcomes than take it or leave it offers
- In both cases, proposers should change their offer according to ex-ante alignment (i.e. bargaining power)
- Theory informs the optimal offer, including when no delegation and full delegation are optimal
- We test if these predictions hold and assess behavioral deviations (e.g. other regarding behavior, optimization failures, etc.)
Experiment
Experimental Design
- Constructed environment that models the veto bargaining framework
- One challenge: how to bring this abstract environment to a participants in a way that is easier to understand?
Experimental Design
- Constructed environment that models the veto bargaining framework
- One challenge: how to bring this abstract environment to a participants in a way that is easier to understand?




Experimental Design
- Constructed environment that models the veto bargaining framework
- One challenge: how to bring this abstract environment to a participants in a way that is easier to understand?




Experimental Design
Proposer
Seller
Vetoer
Buyer
State
Ideal Demand
Offer
Widgets
Delegation
Widget Menu
Types
Urn Draws
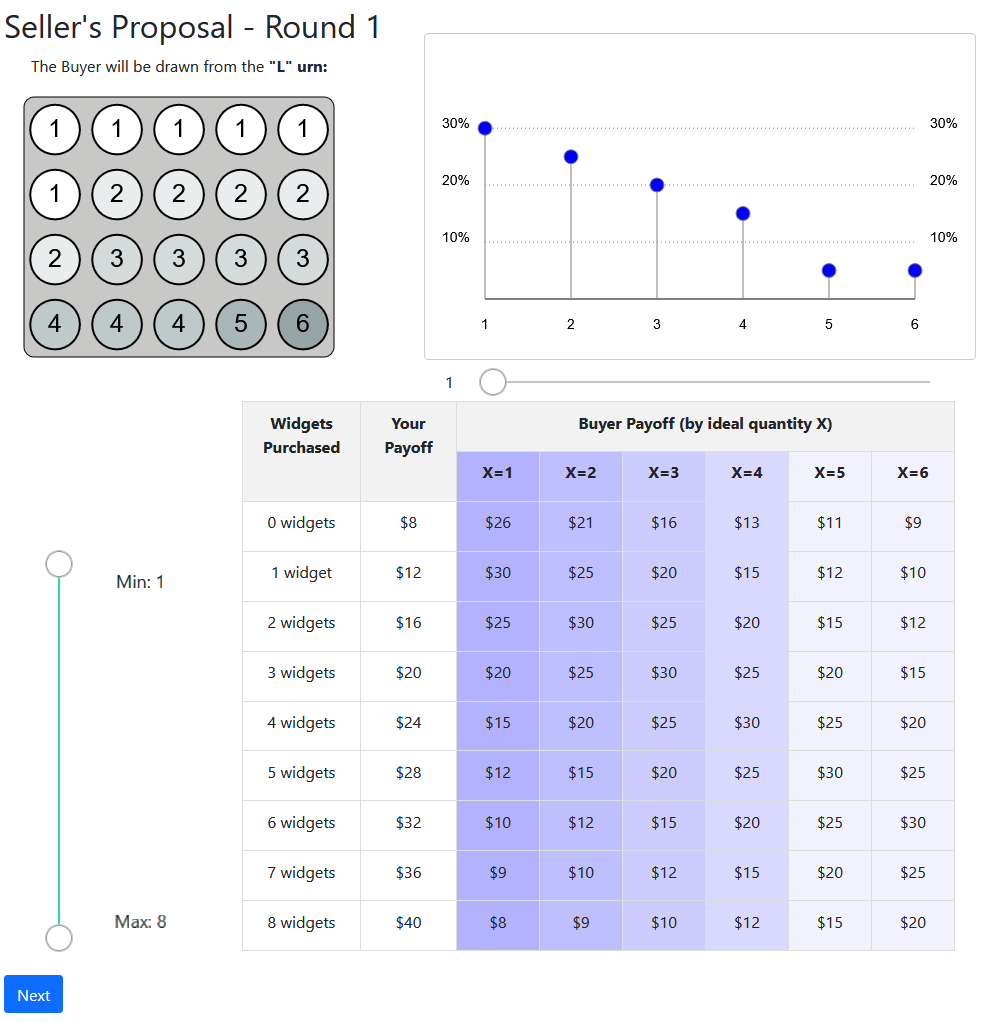



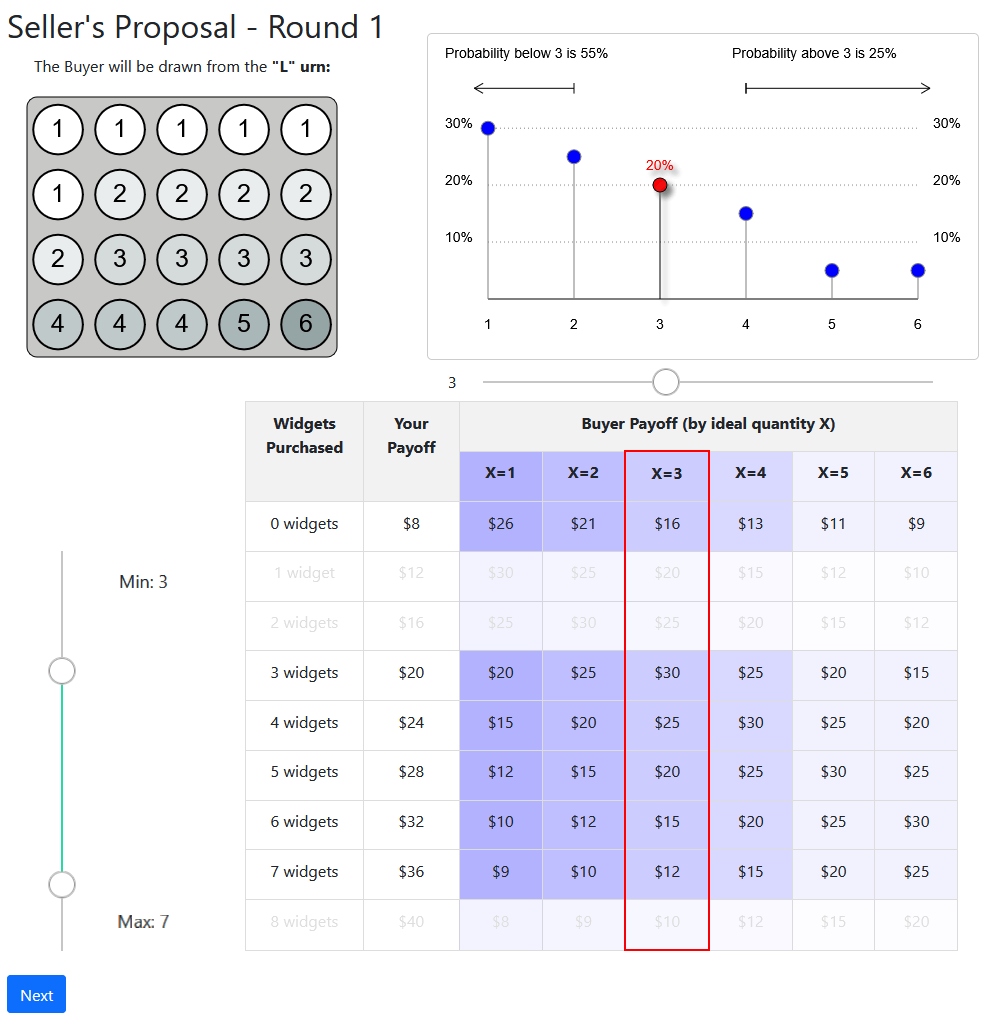
Delegation treatment:
offer a range
Take it or leave it:
single offer
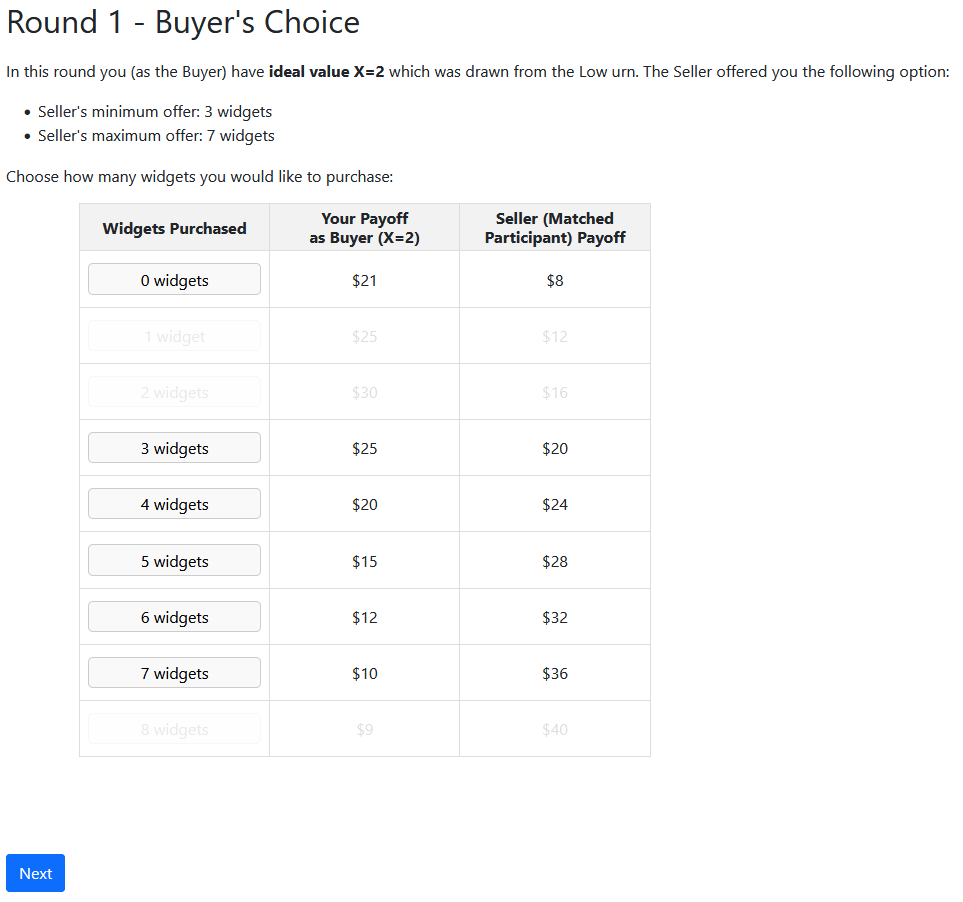
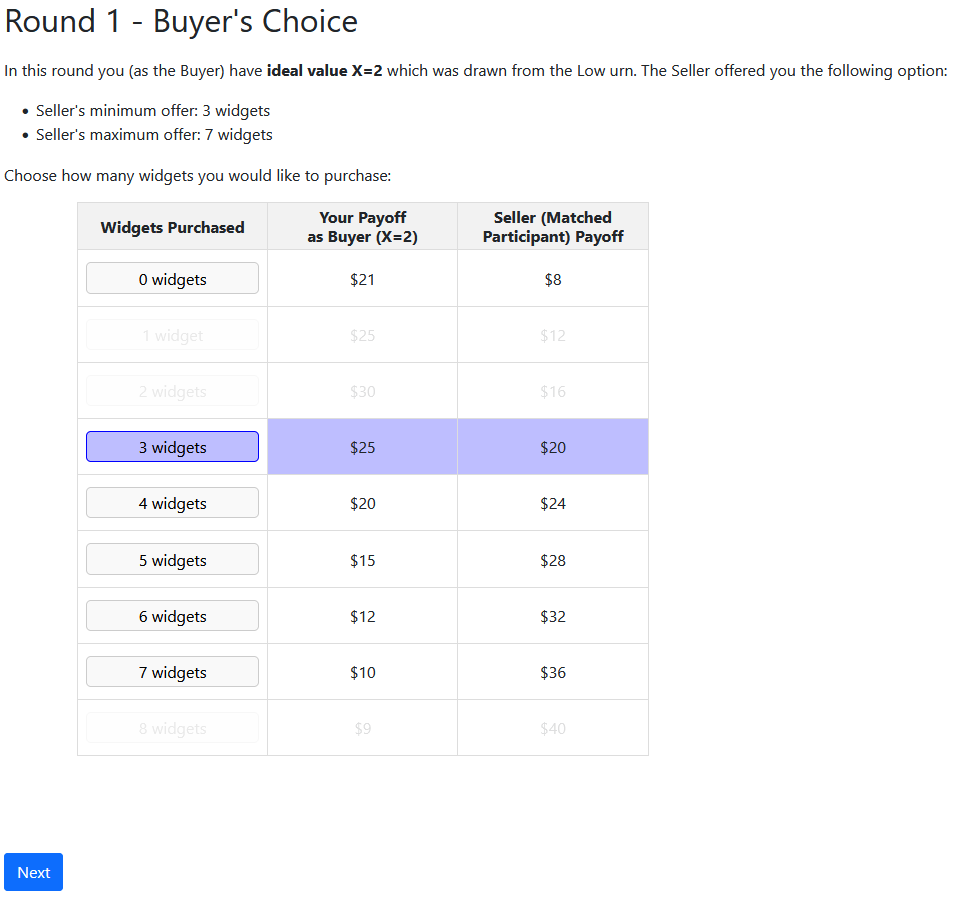

Experimental Design
- Within-subject variation:
- Varying distributions (high, middle, low) for the Buyer
- Changing roles: 5 rounds in one role, 5 rounds in the other, and back to first role for 5 more rounds
- Between subject 2x2
- 12 sessions at the Pittsburgh Experimental Economics Laboratory
| No Chat | Chat | |
| Take-it-or-leave-it | N=66 | N=60 |
| Delegation | N=64 | N=66 |
Experimental Design
- Within-subject variation:
- Varying distributions (high, middle, low) for the Buyer
- Changing roles: 5 rounds in one role, 5 rounds in the other, and back to first role for 5 more rounds
- Between subject 2x2
- Collect other behavioral variables:
- Optimizing ability while playing against a robot Buyer
- Risk-aversion over the same domain
- Other-regardingness also over the same domain
Results
Results: Seller offers in TIOLI



Low
Middle
High
Results: Seller offers in TIOLI



Low
Middle
High
Results: Seller offers in TIOLI

Results: Seller offers in TIOLI

Results: Seller offers in Delegation
Low
Middle
High



Minimal offer in interval:
Results: Seller offers in Delegation
Low
Middle
High



Minimal offer in interval:
Results: Offer comparison over Mechanisms
Low



Middle
High
Results: Offer comparison over Mechanisms
Low



Middle
High
Results: Inefficiency (Theory)

TIOLI
Delegation
Results: Inefficiency (Theory)

TIOLI
Delegation
Results: Inefficiency (Theory)

TIOLI
Delegation
Results: Inefficiency (Data)

TIOLI
Delegation
Effect of Delegation: Theory

Effect of Delegation: Theory

Effect of Delegation: Empirical Payoffs

Results: Key Points
- Offers respond to the distribution of the types in a well-ordered manner
- Offers are more generous than perfectly-optimized predictions
- Proposers/sellers in delegation are more generous
- Delegation mechanism is more efficient than take it or leave it, which is predicted the theory
- Most of the efficiency gains are captured by the vetoer/buyer, which is not predicted by the theory
- Best improvements for the proposer/seller is in the decreasing (low) distribution
Other Results
What is the effect of communication?
- Communication improves bargaining efficiency
- More in take it or leave it case, where we might expect it
- But also in delegation
- Proposers/sellers do worse in the delegation case with chat
Why do we see behavioral deviations from theory?
- Main reason sellers don't extract more of the delegation gain is optimization failure
- Lottery choices indicate less delegation
- Robot choices match behavior in the Delegation game
Appendix:
Conclusion
- Test delegation bargaining with veto power in a lab setting
- Proposers respond to key distribution parameters and change their offers accordingly
- Clear efficiency gains from the delegation mechanism over take-it-or-leave-it offers
- But more of the surplus goes to the responder
- Optimization failures in understanding the mechanism action space explain some of the proposer's failure to extract more
- However, this doesn't lead to inefficiency as they over-delegate
Thank you!
Questions or Comments?
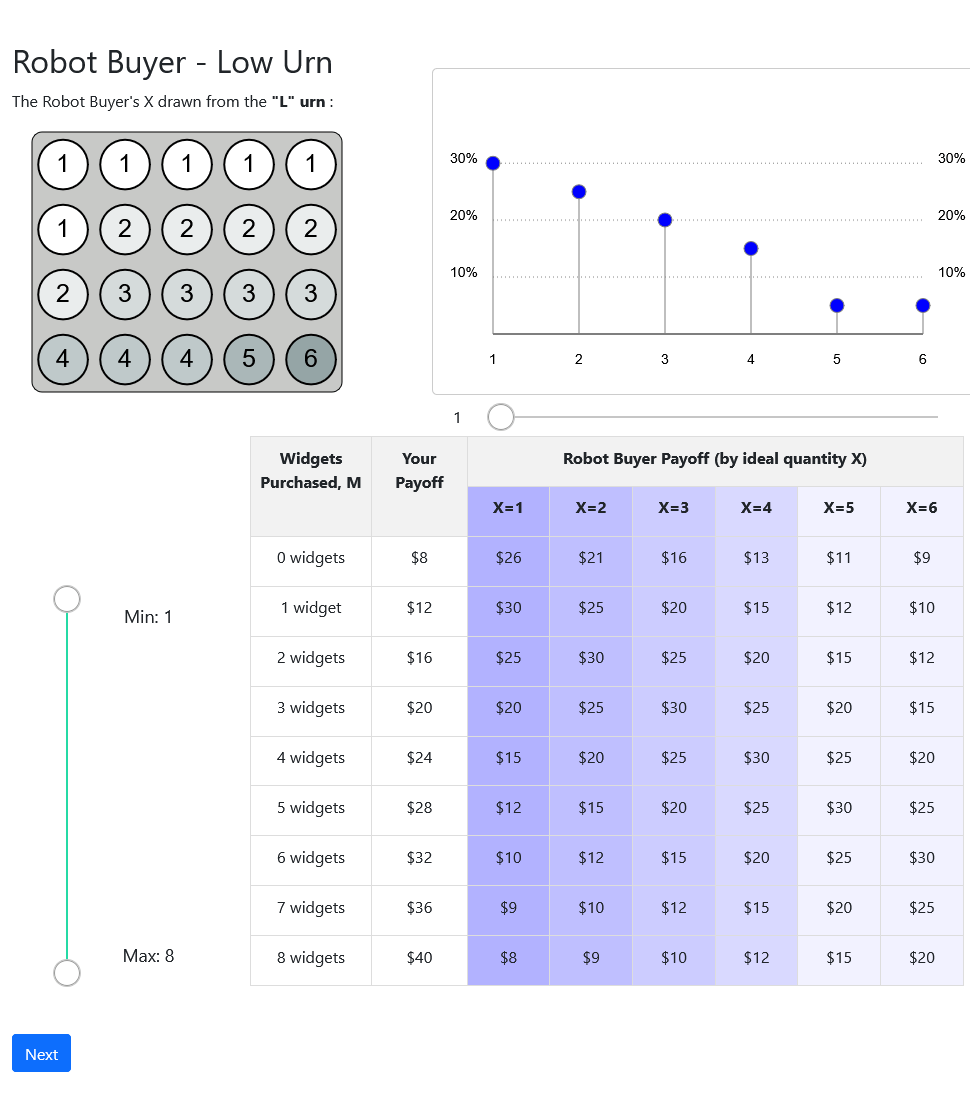
Diagnosing the Failures: Pure Optimization
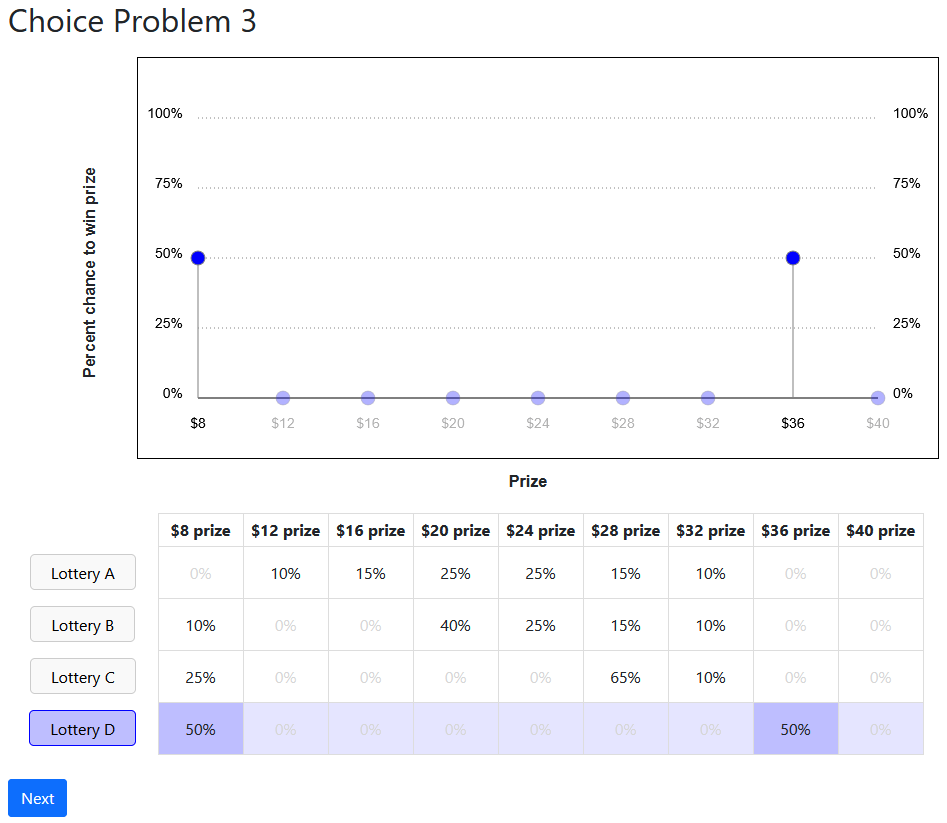
Diagnosing the Failures: Lotteries
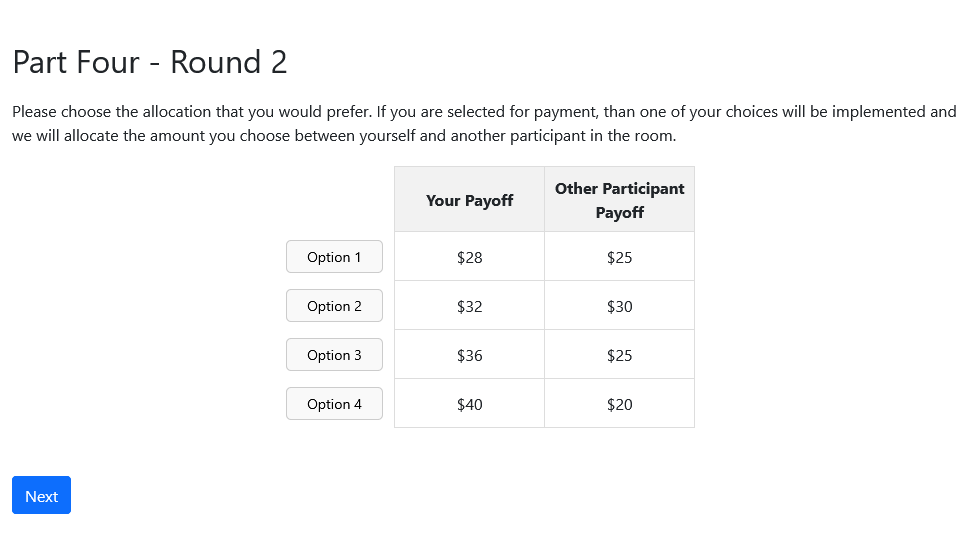
Diagnosing the Failures: Distribution
Results: Inefficiency (Data with No Comm)

TIOLI
Delegation
Results: Inefficiency (Data with Comm)

TIOLI
Delegation
Results: Communication Offers (TIOLI)



Low
Middle
High



Chat
No Chat
Results: Offers (Delegation)



Low
Middle
High



Chat
No Chat
Results: What else is included in interval?

Results: What else is included in interval?

Student Practice Delegation
By bjw95
Student Practice Delegation
- 78



