Eulerian path and circuit

Eulerian Path is a path in graph that visits every edge exactly once. Eulerian Circuit is an Eulerian Path which starts and ends on the same vertex.

Eularian Path

2

1

3

Eularian Path

2

1

3

Eularian Path

2

1

3

Eularian Path

2

1

3

Eularian Cycle

1

4

3

2

Eularian Cycle

1

4

3

2

Eularian Cycle

1

4

3

2

Eularian Cycle

1

4

3

2

Eularian Cycle

1

4

3

2

Eularian Cycle

1

4

3

2

Fleury’s Algorithm

An algorithm to find an Eulerian path or an

Eulerian circuit

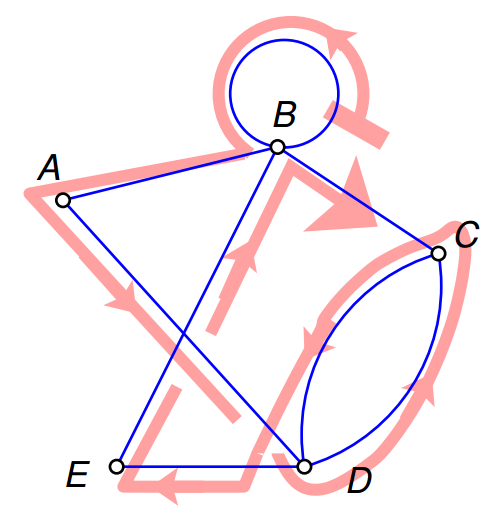
Fleury’s Algorithm

• Make sure the graph has either 0 or 2 odd vertices.

• If there are 0 odd vertices, start anywhere. If there are 2 odd vertices, start at one of them.

• Follow edges one at a time. If you have a choice between a bridge and a non-bridge, always choose the non-bridge.

• Stop when you run out of edges.
  

Example

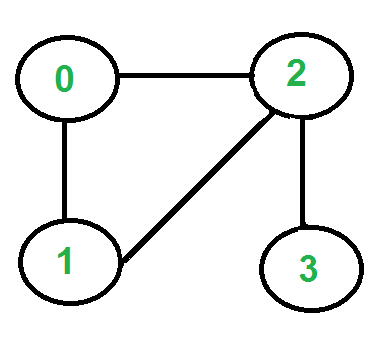
There are two vertices with odd degree, ‘2’ and ‘3’, we can start path from any of them. Let us start tour from vertex ‘2’.

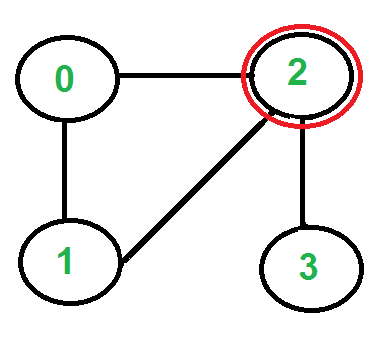
There are three edges going out from vertex ‘2’, which one to pick? We don’t pick the edge ‘2-3’ because that is a bridge (we won’t be able to come back to ‘3’). We can pick any of the remaining two edge. Let us say we pick ‘2-0’. We remove this edge and move to vertex ‘0’.

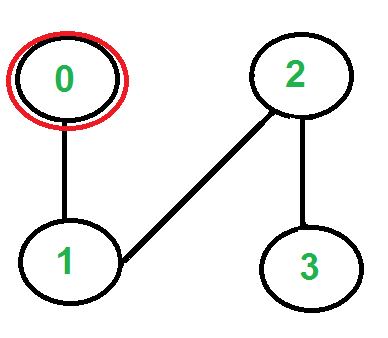
There is only one edge from vertex ‘0’, so we pick it, remove it and move to vertex ‘1’. Euler tour becomes ‘2-0 0-1’.

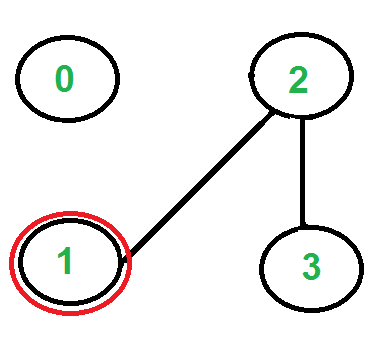
There is only one edge from vertex ‘1’, so we pick it, remove it and move to vertex ‘2’. Euler tour becomes ‘2-0 0-1 1-2’

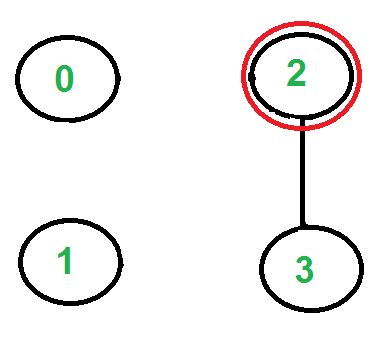
Again there is only one edge from vertex 2, so we pick it, remove it and move to vertex 3. Euler tour becomes ‘2-0 0-1 1-2 2-3’

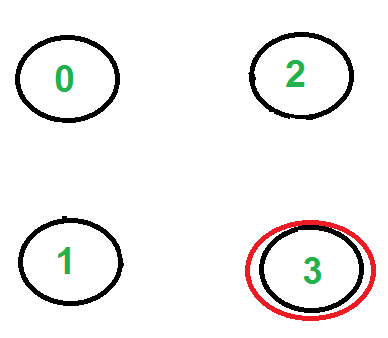
There are no more edges left, so we stop here. Final tour is ‘2-0  0-1  1-2  2-3’.

Example

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

1

4

3

2

5

6

9

7

8

Example

3

1

2

4

5

Example

3

1

2

4

5

Example

3

1

2

4

5

Example

3

1

2

4

5

Example

3

1

2

4

5

Example

3

1

2

4

5

Example

3

1

2

4

5

Example

3

1

2

4

5

Example

3

1

2

4

5

Example

3

1

2

4

5