Deep, Skinny
Neural Networks
are not Universal Approximators
by Jesse Johnson
Presented by Breandan Considine
\mathbb{R}^k : \text{Parameter space}
\mathbb{R}^n : \text{Input space}
\mathbb{R}^m : \text{Output space}
\varphi : \mathbb{R} \rightarrow \mathbb{R}, \text{Activation function}
n_1, \ldots, n_{\kappa-1} : \text{Hidden layers}
\mathcal{N}_{\varphi, n}^* : \text{Family of skinny nets, i.e. the union of all model}
\text{families } \mathcal{N}_{\varphi, n_0, n_1, ..., n_{\kappa-1}, 1} \mid n_i \leq n \forall i \in [0, \kappa)
\mathcal{N}_{\varphi, n_0, n_1, ..., n_{\kappa-1}, 1} : \text{Family of functions defined by a}
\text{FF neural network with } n_0 \text{ inputs and } n_\kappa \text{ outputs}
\hat\mathcal{N}_{n} : \text{Union of all non-singular functions in families } \mathcal{N}_{\varphi, n}
For a neural network with a one-dimensional output, if:
- the hidden layers are all the same dimension
- the weight matrices are all non-singular
- the activation function is one-to-one
Then the composition of all the functions up to last linear function will be one-to-one as well. The last linear function is a 1D projection, so the preimage of any point into the last hidden layer is a hyperplane. The preimage of this hyperplane in the one-to-one map may not be a hyperplane, but it will be an unbounded subset of the domain.
Definition 1. We will say that a function \(f: \mathbb{R}\rightarrow\mathbb{R}\) has unbounded level components if for every \(y\in\mathbb{R}\), every path component of \(f^{-1}(y)\) is unbounded.
Level set: intersection between hyperplane and function
Connected path: We can reach any point from every other point through a continuous path
(straight line alone is not a component by itself)
Disjoint components
Connected path: We can reach any point from every other point
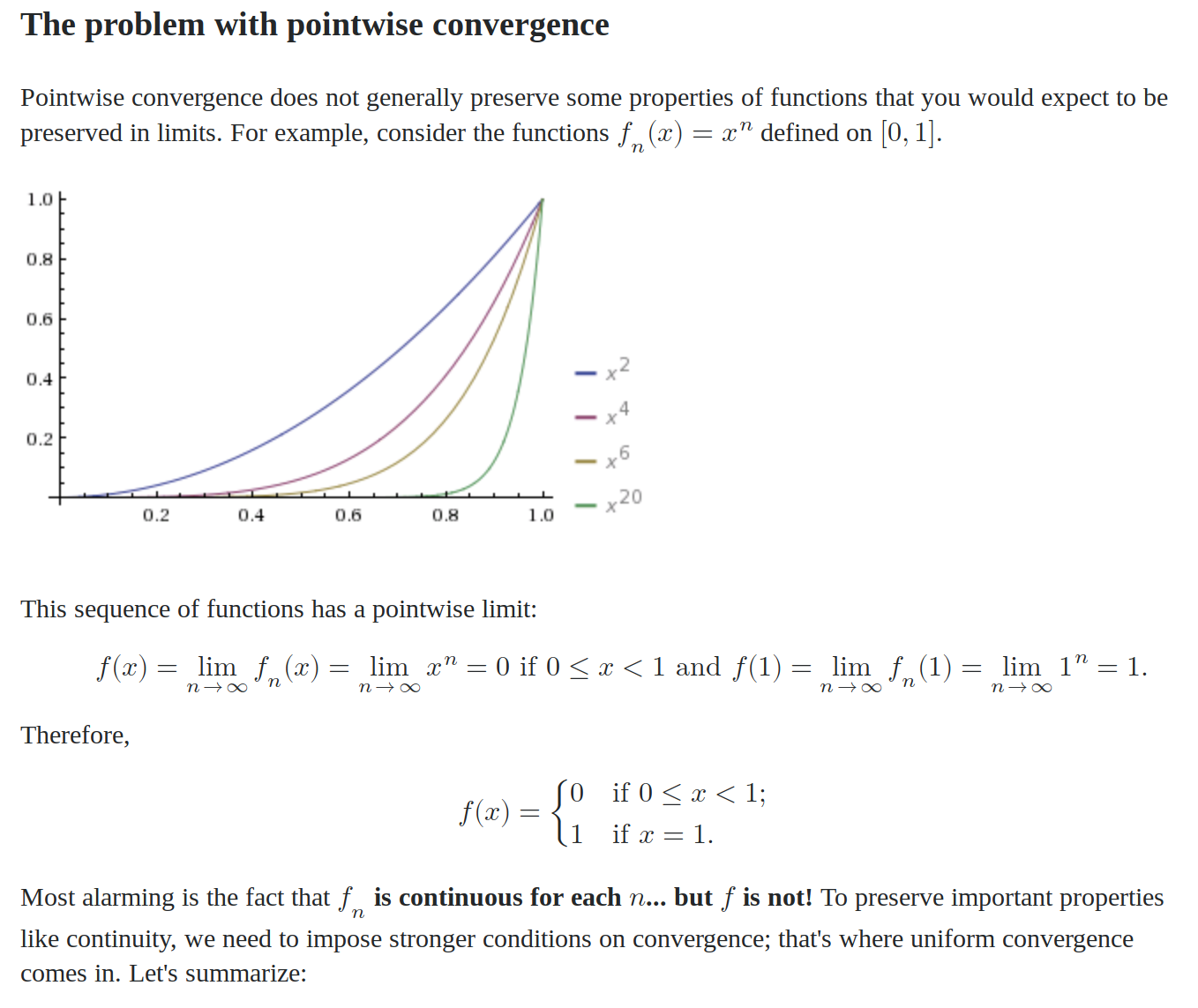
Theorem 1. For any integer \(n \geq 2\) and uniformly continuous activation function \(\varphi: \mathbb{R}\rightarrow\mathbb{R}\) that can be approximated by one-to-one functions, the family of layered feed-forward neural networks with input dimension \(n\) in which each hidden layer has dimension at most \(n\) cannot approximate any function with a level set containing a bounded path component.
The proof of Theorem 1 has three parts:
- If a function can be approximated by \(\mathcal{N}_{\varphi, n}^*\) then it can be approximated by the smaller model family of non-singular layers (L2)
- Therefor it can be approximated by functions with unbounded level components (L4)
- Therefor it must also have unbounded level components (by contradiction). (Lemma 5)
Define the model family of non-singular functions \(\hat\mathcal{N}_{n}\) to be the union of all non-singular functions in families \(\mathcal{N}_{\varphi, n}^*\) for all activation functions \(\varphi\) and a fixed \(n\).
Lemma 2. Lemma 2. If \(g\) is approximated by \(\mathcal{N}_{\varphi, n}^*\) for some continuous activation function \(\varphi\) that can be uniformly approximated by one-to-one functions then it is approximated by \(\hat\mathcal{N}_{n}\).
Lemma 4. If \(f\) is a function in \(\hat\mathcal{N}_{n}\) then every level set \(f^{-1}(y)\) is homeomorphic to an open (possibly empty) subset of \(\mathbb{R}^{n-1}\). This implies that \(f\) has unbounded level components.
Take \(X=(0,\infty)\) in a metric space.
- \([1,2]\) is a closed, bounded and compact set in \(X\).
- \((0,1]\) is a closed and bounded set in \(X\), which is not compact (e.g. \((0,1]\subseteq\bigcup_n(1/n,2)\)).
- \([1,\infty)\) is a closed, but unbounded and not compact set in \(X\).
- \((1,\infty)\) is an unbounded set which is neither closed nor compact in \(X\).
- \((1,2)\) is neither closed nor bounded in \(X\), and it's not compact.
No unbounded set or not closed set can be compact in any metric space.
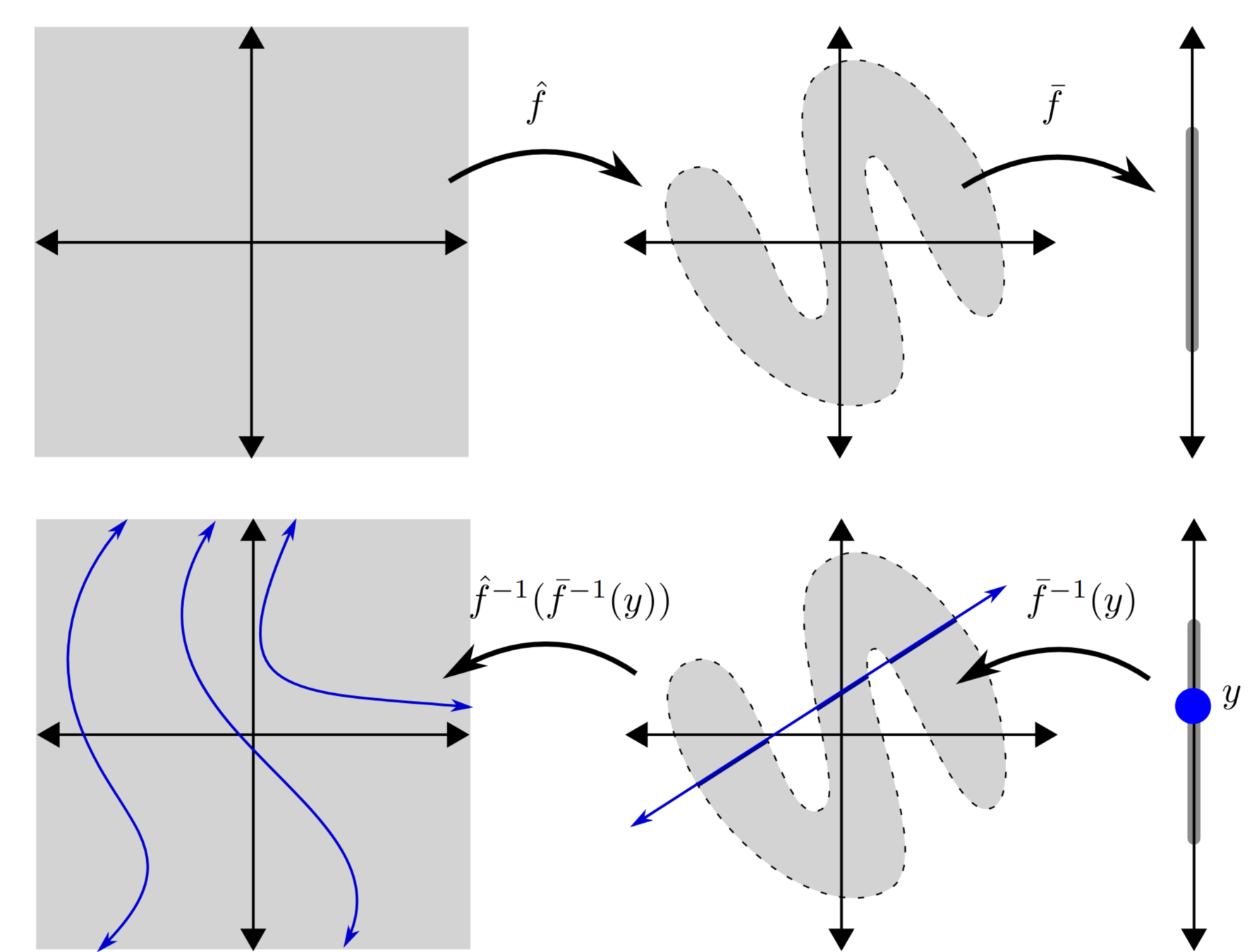
Proof. Recall by definition \(f\) is a non-singular function in \(\hat\mathcal{N}_{n}\), where \(\varphi\) is continuous and one-to-one. Let \( \hat f : \mathbb{R}_n \rightarrow \mathbb{R}_n \) be the function defined by all but the last layer of the network. Let \( \overline f : \mathbb{R}_n \rightarrow \mathbb{R}_n \) bethe function defined by the map from the last hidden layer to the final output layer so that \(f=\overline f \circ \hat f\).
Because \(f\) is nonsingular, the linear functions are all one-to one. Because \(\varphi\) is continuous and one-to-one, so are all the non-linear functions. Thus the composition \(\hat f\) is also one-to-one, and therefore a homeomorphism from \(\mathbb{R}^n\) onto its image \(I_{\hat f}\).
Since \(\mathbb{R}^n\) is homeomorphic to an open n-dimensional ball, \(I_{\hat f}\) is an open subset of \(\mathbb{R}^n\), as indicated in the top row of Figure 1.
The function \(\overline f\) is the composition of a linear function to \(\mathbb{R}\) with \(\varphi\), which is one-to-one by assumption. So the preimage \(\overline f ^{-1}(y)\) for any \(y \in \mathbb{R}\) is an (n−1)-dimensional plane in \(\mathbb{R}^n\). The preimage \( f ^{-1}(y)\) is the preimage in \(\hat f \) this (n−1)-dimensional plane, or rather the preimage of the inter-section \(I_{\hat f}\cap \overline f ^{-1}(y)\), as indicated in the bottom right/center of Figure 2. Since \(I_{\hat f}\) is open as asubset of \(\mathbb{R}^n\), the intersection is open as a subset of ̄\( f ^{-1}(y)\).
Since \(\hat f\) is one-to-one, its restriction to this preimage (shown on the bottom left of the Figure) is a homeomorphism from \( f^{-1}(y)\) to this open subset of the \((n−1)\)-dimensional plane \(f^{−1}(y)\). Thus \(f^{−1}(y)\)is homeomorphic to an open subset of \(\mathbb{R}^{n−1}\).
Finally, recall that the preimage in a continuous function of a closed set is closed, so \(f^{−1}(y)\) is closed as a subset of \(\mathbb{R}^n\). If it were also bounded, then it would be compact. However, the only compact, open subset of \(\mathbb{R}^{n−1}\) is the empty set, so \(f^{−1}(y)\) is either unbounded or empty. Since each path component of a subset of \(\mathbb{R}^{n−1}\) is by definition non-empty, this proves that any component of \(f\) is unbounded. \(\square\)
Deep, Skinny Neural Networks are not Universal Approximators
By Breandan Considine
